数字信号处理基础全解

数字信号处理知识点总结数字信号处理技术为人们提供了处理和分析信号的便利方式，同时也加快了信号的传输速度和提高了传输质量。

数字信号处理技术在多个领域都有着广泛的应用，比如图像处理、音频处理、通信系统、雷达系统、生物医学信号处理等等。

在这些领域中，数字信号处理技术能够对信号进行分析、滤波、编码、解码、压缩等处理，从而提高系统性能和降低成本。

数字信号处理的基础知识点主要包括以下几个方面：1. 信号和系统基础：信号与系统是数字信号处理的基础，需要深入理解信号的特性和系统的行为。

信号与系统的基本概念包括信号的分类、时域和频域分析、连续时间信号和离散时间信号、因果性、稳定性等等。

2. 采样和量化：采样是将连续时间信号转换为离散时间信号的过程，而量化是将模拟信号转换为数字信号的过程。

采样和量化的基本概念包括采样定理、采样率和量化精度。

3. 离散时间信号的表示和运算：离散时间信号可以用离散时间单位冲激函数的线性组合表示，同时可以进行离散时间信号的运算，比如线性和、线性积分、线性差分等。

4. 离散时间系统的性质和分析：离散时间系统的特性包括线性性、时不变性、因果性、稳定性等，同时还需要对离散时间系统进行频域和时域分析。

5. 离散傅里叶变换（DFT）：DFT 是将离散时间信号转换到频域的一种方法，它可以帮助分析信号的频率分量和谱特性。

6. Z变换：Z 变换是将离散时间信号转换到 Z 域的一种方法，它可以帮助分析离散时间系统的频域特性。

7. 数字滤波器设计：数字滤波器设计是数字信号处理中非常重要的一部分，它包括有限脉冲响应（FIR）滤波器和无限脉冲响应（IIR）滤波器的设计方法。

8. FFT 算法：快速傅里叶变换（FFT）是一种高效的计算 DFT 的算法，它能够大大提高傅里叶变换的计算速度。

9. 数字信号处理系统的实现：数字信号处理系统的实现可以通过软件方式和硬件方式两种方法进行，比如使用 MATLAB、C 语言等软件实现，或者使用专用的数字信号处理器（DSP）进行硬件实现。

数字信号处理数字信号处理（Digital Signal Processing，简称DSP）是指通过数学运算和算法实现对数字信号的分析、处理和改变的技术。

它广泛应用于通信、音频、视频、雷达、医学图像等领域，并且在现代科技发展中发挥着重要作用。

本文将介绍数字信号处理的基本原理和应用，以及相关的算法和技术。

一、数字信号处理的基本原理数字信号处理的基本原理是将连续的模拟信号转换为离散的数字信号，再通过算法对数字信号进行处理。

这个过程主要包括信号采样、量化和编码三个步骤。

1. 信号采样：信号采样是指以一定的时间间隔对连续的模拟信号进行离散化处理，得到一系列的采样点。

通过采样，将连续的信号转换为离散的信号，方便进行后续的处理和分析。

2. 量化：量化是指对采样得到的信号进行幅度的离散化处理，将连续的幅度变为离散的幅度级别。

量化可以采用线性量化或非线性量化的方式，通过确定幅度级别的个数来表示信号的幅度。

3. 编码：编码是指对量化后的信号进行编码处理，将其转换为数字形式的信号。

常用的编码方式包括二进制编码、格雷码等，在信息传输和存储过程中起到重要作用。

二、数字信号处理的应用领域数字信号处理被广泛应用于各个领域，以下介绍几个主要的应用领域：1. 通信领域：在通信领域中，数字信号处理用于信号的调制、解调、编码、解码等处理过程。

通过数字信号处理，可以提高通信系统的性能和可靠性，实现高速、高质量的数据传输。

2. 音频和视频处理：在音频和视频处理领域，数字信号处理可以用于音频和视频的压缩、解压、滤波、增强等处理过程。

通过数字信号处理，可以实现音频和视频信号的高保真传输和高质量处理。

3. 医学图像处理：在医学图像处理领域，数字信号处理可以用于医学图像的增强、分割、识别等处理过程。

通过数字信号处理，可以提高医学图像的质量和准确性，帮助医生进行疾病的诊断和治疗。

4. 雷达信号处理：在雷达领域，数字信号处理可以用于雷达信号的滤波、目标检测、跟踪等处理过程。

数字信号处理基础理论第一部分：数字信号的概念数字信号是表示物理量、物理现象或信息的数值序列。

数字信号的基本特点是离散、数字、有限。

离散表示信号的时间和幅度均是离散的，数字表示信号的幅度值是由有限位数的二进制数表示的，有限表示信号的时间和幅度序列都是有限长的。

数字信号与模拟信号的差异在于数字信号可以通过计算机或数字信号处理器进行处理和传输。

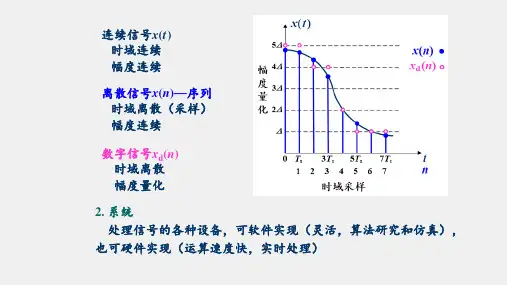
数字信号可以是连续时间（C-T）系统的采样信号，也可以是离散时间（D-T）系统的离散信号。

其中，离散信号包括从连续时间信号通过采样和量化转换得到的离散信号和由数字系统产生的数字信号。

第二部分：采样与量化采样是指将连续时间信号转化为离散时间信号的过程。

采样信号的采样周期是指连续时间信号在采样过程中，采样时刻的时间间隔。

采样周期决定了采样后的离散信号的频率分辨率，即在频率域上连续时间信号的频谱密度分布情况。

量化是指对采样信号的幅度进行离散化处理，将其表示为有限位数的数字。

量化误差是指离散信号与采样信号之间的误差，通常用均方误差来描述。

采样与量化过程是数字信号处理的基础，采样定理是数字信号处理中的重要理论基础。

根据采样定理，对于一个具有有限带宽的信号，只要采样频率大于等于信号带宽的两倍，就能够完全重构原信号，避免产生采样失真和折叠失真的问题。

第三部分：信号处理数字信号处理中的信号处理包括线性与非线性、时不变与时变、因果与非因果等多个方面。

其中，线性与非线性处理是数字信号处理领域中的基本概念之一。

线性系统能够满足叠加原理和时移不变性等性质，而非线性系统则不能。

时不变系统的性质是在时间轴上发生平移不会使系统发虚发生任何变化，而时变系统则不同，其系统参数是随时间改变的。

因果系统是指系统的响应只依赖于过去或现在的输入信号，与未来输入信号无关。

系统稳定性是指系统在固定的输入条件下能够保持稳定，不发生发散、爆炸或周期性振荡等现象。

数字信号处理的常见应用包括信号滤波、时域变换、频域变换等。

数字信号处理（DSP）基础 Digital Signal Processing编写：刘馥清模拟信号与数字信号（基本术语）过程：物理量（位移、速度、加速度、声压、声强、声功率、压强、应力、应变、温度…）随时间变化的历程。

信息：研究问题所关心的过程特征。

信号：指物理过程通过传感器（也称换能器）转换成的电信号。

信号是信息的载体。

信号处理即从信号获取有用信息。

连续信号：幅值随时间连续变化的信号。

离散信号：只在离散时刻取值的信号。

通常对连续信号采（抽）样而得到。

模拟信号：未经数字化处理的连续信号。

数字信号：数字化的离散信号，适用于计算机处理。

A/D ：Analog to Digital Conversion注：数字信号处理的重要基础——傅里叶变换： 对连续信号 )()(f X t x ⇔FT ： ()()[]dt et x t x F f X ftπj2)(−∞∞−∫== IFT ： []df e f X f X Ft x ftπj21)()()(∫∞∞−−== 对数字信号 {}{}k n X x ⇔DFT ： Nnk N n n k k x f k X f X X /j210e N 1)()(π−−=∑=∆== ( k = 0,1,… N-1 ）IDFT ： N nk N k kn n Xt n x t x x /j21e )()(π∑−==∆== ( n = 0,1, … N-1 )物理过程与信号的分类 （一）简谐过程两种数学表达形式1 三角函数形式()()ϕω+=t A t x sinA —振幅ϕ—初相角 ω—角频率(rad/s ) ω= 2πƒ = 2π/T f —频率(Hz) T —周期（s ）2 复指数形式()()1−===+j e A Ae t x tj t j ωϕω其中 ϕj Ae A = ——复振幅（复振幅是相量—Phasor ，有别于矢（向）量—Vector ） 相互关系：()t A t A t A ωϕωϕϕωsin cos cos sin sin +=+t A t A ωωsin cos 21+= ϕϕϕsin cos jA A Ae j +=)(sin )(cos t ϕϕϕ+++=+ωt jA ωt A Ae )j(ω欧拉公式的几何意义：()()t j t j tj t j eA e A e e A t A ωωωωω−−+=+=222cos 1111()⎟⎠⎞⎜⎝⎛−−⎟⎠⎞⎜⎝⎛−−−=−=212222222sin πωπωωωωt j t j tj t j e A eA e e j A t A⎟⎠⎞⎜⎝⎛−=−=21πj ej j，2221A A A += ，21A A arctg=ϕ欧拉公式的几何意义周期过程展开为傅里叶级数周期信号()()kT t x t x += k —整数 ， T —周期令 T πω21=（称为基频） ，则 ()t x 可展开为 傅里叶三角级数：()()∑∞=++=1110sin cos n n n tn b t n a a t x ωω()∑∞=++=110sin n n n t n c c ϕω其中 00a c = ， 22n n n b a c += ，n nn b a arctg =ϕ ∫−=2201TT td x T a ∫−=221cos 2TT n td t n x T a ω ∫−=221sin 2TT n td t n x T b ω( n = 1、2、3、…… )傅里叶级数的复指数形式Fourier series 缩写为FS()()[]∑∞=−−++=1011n tn j n t jn n e X e X X t x ωω或 ()∑∞−∞==n tn j n eX t x 1ω()∫−=2211TT t n j n td e t x T X ω其中nn j n j n n e X e X X ϕϕ==n n n n n c b a X X 212122=+==*n n X X −= , ——即 n X − 为 n X 的共轭复数：()n n n jb a X −=21()n n n jb a X +=−21n nn n b a arctg=−=−ϕϕ000c a X == ， 00=ϕ周期过程相量频谱的三维表示周期信号的特征参数1 峰值px ( p ： peak ) 峰峰值pp x −2 平均绝对值avx ( av ： average )td x T x Tav ∫=013 均值x µ 或 x (µ： mean )td x T x Tx ∫==01µ000X c a x ===µ ( 称直流分量或DC 分量 )4 均方值（平均功率）P 或 2x （p ： power ）t d x Tx P T ∫==0221∑∑∑∞−∞=∞−∞=∞=⋅==⎟⎠⎞⎜⎝⎛+=n nn n n n n X X X c c P *221225 均方根值（有效值）rmsx ( rms ： root of mean square )∫=T rmsdt x T x 021 正弦信号：p p rms x x x 707.022==pp av x x x 637.02==π111.142==πav rms x x周期矩形波的幅值谱和功率谱()∑∞−∞==n tn j neX t x 1ω平均功率为：∑∑∑∞−∞=∞−∞=∞−∞==⋅==n nn nn n nS X X X P *2双边功率谱： 2*nn n n X X X S =⋅= n = 0,±1,±2,…单边功率谱：⎪⎩⎪⎨⎧>====022020n c S n c S G n n n n例：周期矩形波(a) 双边幅值谱(b)双边功率谱(c)单边功率谱(d)有效值谱傅里叶变换非周期过程：令 ∞→T ,ωπωd T →=21, ωω→1n ，∫→∑, ()()ωωωd X n X X n ⋅→=1()∫−−=2211TT t jn n td e t x T X ω→()()∫∞∞−−=td e t x X t j ωπω21()∑∞−∞==n tjn ne X t x 1ω→()()∫∞∞−=ωωωd e X t x t j令 ()()ωπX f X 2=，f πω2=， df d πω2=则 ()=f X ()[]()∫∞∞−−=t d e t x t x F t f j π2()()[]()∫∞∞−−==f d e f X f X Ft x t f j π21FT()t x ()f XIFTFT : Fourier Transform 傅里叶变换 IFT ： Inverse Fourier Transform 傅里叶逆变换矩形脉冲的傅里叶频谱矩形脉冲()⎪⎪⎩⎪⎪⎨⎧>≤=20,2ττt t A t x()()[]()f f A t x F f X πτπττsin ==()()()f j e f X f X ϕ=幅值谱 ()()ff A f X πτπττsin = 相位谱()()⎪⎪⎩⎪⎪⎨⎧+≤≤++≤≤=ττπττϕ1212,,122,0n f n n f nf n 为整数(a)幅值谱(b) 相位谱(c)相量谱ESD & PSD● 对能量有限信号，如瞬态信号如果()()f X t x FT⎯→⎯ 则取 ()()()f X f X f S x*⋅= 称之为()t x 的能量谱密度函数或ESD (Energy Spectrum Density )。

目录1 数字信号处理基本内容 (2)2数字滤波器 (3)2.1 滤波器的分类 (3)2.2 FIR滤波器和IIR滤波器 (4)2.3 FIR滤波器和IIR滤波器的FPGA实现 (4)3 傅里叶变换 (8)3.1 连续傅里叶变换 (8)3.2傅里叶级数 (9)3.3离散傅里叶级数 (9)3.4离散时间傅里叶变换 (9)3.5离散傅里叶变换 (9)3.6 快速傅里叶变换 (10)3.7分数傅里叶变换 (10)3.8短时距傅里叶变换 (11)3.9小波分析 (11)3.10 离散小波变换 (12)3.11 Z变换 (14)3.12拉普拉斯变换 (14)3.13 傅里叶变换的硬件实现 (14)4谱分析 (15)4.1谱分析的实现 (15)4.2 随机信号处理概述 (15)4.3随机信号谱分析 (16)5数字信号处理研究内容总结 (17)1 数字信号处理基本内容数字信号处理主要是研究有关数字滤波技术、离散变换快速算法和谱分析方法。

数字信号处理主要内容①离散线性时不变系统理论（包括时域、频域、各种变换域）②频谱分析（包括有限字长效应）：FFT谱分析方法及统计分析方法③数字滤波器设计及滤波过程的实现（包括有限字长效应）④时频-信号分析（短时付氏变换）…Short Fourier Transform‟，小波变换(Wavelet Analysis), Wigner Distribution⑤多维信号处理（压缩与编码及其在多煤体中的应用）⑥非线性信号处理⑦随机信号处理⑧模式识别人工神经网络⑨信号处理单片机(DSP)及各种专用芯片(ASIC)，信号处理系统实现2数字滤波器2.1 滤波器的分类（1）根据滤波器的选频作用分为低通、高通、带通和带阻滤波器四种。

（2）根据“最佳逼近特性”的标准进行分类：巴特沃兹滤波器：从幅频特性提出要求，而不考虑相频特性。

其幅频响应为：切比雪夫滤波器：切贝雪夫滤波器也是从幅频特性方面提出逼近要求的，其幅频响表达式为：贝塞尔滤波器：只满足相频特性而不关心幅频特性。