高二数学下册期末检测试题4

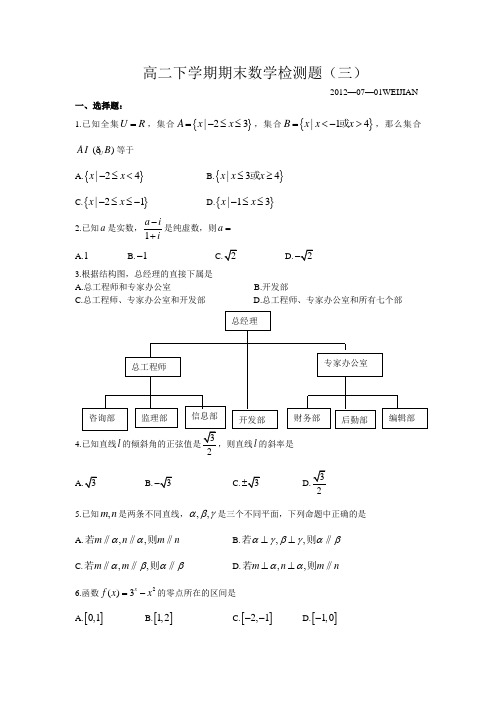
高二下学期期末数学检测题（三）2012—07—01WEIJIAN一、选择题：1.已知全集U R =，集合{}|23A x x =-≤≤，集合{}|14B x x x =<->或，那么集合()U A B ð等于A.{}|24x x -≤<B.{}|34x x x ≤≥或C.{}|21x x -≤≤-D.{}|13x x -≤≤2.已知a 是实数，1a i i -+是纯虚数，则a = A.1 B.1-D. 3.根据结构图，总经理的直接下属是A.总工程师和专家办公室B.开发部C.总工程师、专家办公室和开发部D.总工程师、专家办公室和所有七个部2B. C. D.25.已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是A.,,m n m n αα若则‖‖‖B.,,αγβγαβ⊥⊥若则‖C.,,m m αβαβ若则‖‖‖D.,,m n m n αα⊥⊥若则‖ 6.函数2()3x f x x =-的零点所在的区间是A.[]0,1B.[]1,2C.[]2,1--D.[]1,0-7.张华同学对命题：“1()x x f x e e=+在()0,+∞上是增函数”给出如下证明： 1()x x f x e e =+ /1()x x f x e e∴=- 0x > 1,01x x e e ∴><< 10x x e e ∴-> 即/()0f x >， ()f x ∴在()0,+∞上是增函数.她使用的证明方法是 A.综合法B.分析法C.反证法D.归纳法 8.12ax y x +=+在()2,-+∞上为增函数，则a 的取值范围 A.102a << B.1a <-或12a > C.12a > D.2a >- 9.一个四面体的6条棱中，有3条长为1，有2a ，当体积最大时，a 的值为A.210.过点(11,2)A 作圆22241640x y x y ++--=的弦，其中弦长为整数的共有A.16条B.17条C.32条D.34条11.在同一平面直角坐标系中，函数()y g x =的图象与x y e =的图象关于直线y x =对称。

2020-2021学年高二数学下学期期末考试试题 (IV)本试卷满分150分，考试时间120分钟一、选择题（每小题5分，共60分）1．若集合{}{}084|,51|<+-=<-=x x B x x A ，则=B A （ ） A ．{}6|<x x B ．{}2|>x x C ．{}62|<<x x D ． ∅ 2．函数)4(log 3-=x y 的定义域为 （ ）A ．RB ．),4()4,(+∞-∞C ．)4,(-∞D ． ),4(+∞3．某电视台在娱乐频道节目播放中，每小时播放广告20分钟，那么随机打开电视机观看这个频道看到广告的概率为 （ ）A ．12 B ．13 C ．14D ．164．在等比数列{}n a 中，*0()n a n N >∈且,16,464==a a 则数列{}n a 的公比q 是（ ）A ．1B ．2C ．3D ．45．已知3(,sin ),2a α=1(cos ,)3b α=且//,a b 则锐角α的大小为 （ ） A ．4πB ．3πC ．6πD ．125π6．按照程序框图(如右图)执行， 第3个输出的数是( ).A ．3B ．4C ．5D ．67．如图所示，一个空间几何体的正视图和侧视图都是边长为2的正方形，俯视图 是一个圆，那么这个几何体的体积为 （ ） A ．2πB ．πC ．2πD ．4π8．已知函数b x x x f +-=2)(2在区间)4,2(内有唯一零点，则b 的取值范围是（ ） A ． R B ．)0,(-∞ C ．),8(+∞- D ．)0,8(-9.若实数,x y 满足约束条件222x y x y ≤⎧⎪≤⎨⎪+≥⎩，则目标函数2z x y =+的最大值为（ ）A. 6B. 5C. 4D. 3 10.已知长方体的相邻三个侧面面积分别为6,3,2,则它的体积是( )A ．5B ．6 C.5 D ．611．三个数21log ,)21(,33321===c b a 的大小顺序为 （ ）A ．a c b <<B ．a b c <<C ．b a c <<D ．c a b <<12．设函数x x f 6sin )(π=，则)2009()3()2()1(f f f f ++++ 的值等于( )A ．21B ．23C ．231+ D ．32+二、填空题（每小题5分，共20分）13．已知函数1322(),log (21)2x xe xf x x -⎧<=⎨-≥⎩则=))2((f f ．14．在⊿ABC 中，已知====c C b a 则,3,4,3π．15. 已知5sin =5α则44sin cos αα-的值是 . 16．某厂生产A 、B 、C 三种不同型号的产品，产品数量之比依次为2：3：5．现用分层抽样的方法抽取一个容量为n 的样本，样本中A 种型号产品有16件，则样本容量n ＝ ． 三、解答题：(共70分)解答应写出文字说明、证明过程或演算步骤。

2023-2024学年重庆市高二（下）期末考试数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知f′(x)是函数f(x)的导函数，则满足f′(x)=f(x)的函数f(x)是( )A. f(x)=x 2B. f(x)=e xC. f(x)=lnxD. f(x)=tanx2.如图是学校高二1、2班本期中期考试数学成绩优秀率的等高堆积条形图，如果再从两个班中各随机抽6名学生的中期考试数学成绩统计，那么( )A. 两个班6名学生的数学成绩优秀率可能相等B. 1班6名学生的数学成绩优秀率一定高于2班C. 2班6名学生中数学成绩不优秀的一定多于优秀的D. “两班学生的数学成绩优秀率存在差异”判断一定正确3.对于函数f(x)=x 3+bx 2+cx +d ，若系数b ，c ，d 可以发生改变，则改变后对函数f(x)的单调性没有影响的是( )A. bB. cC. dD. b ，c4.某地根据以往数据，得到当地16岁男性的身高ycm 与其父亲身高xcm 的经验回归方程为y =1417x +29，当地人小王16岁时身高167cm ，他父亲身高170cm ，则小王身高的残差为( )A. −3cmB. −2cmC. 2cmD. 3cm5.若函数f(x)=(x 2+bx +1)e x ，在x =−1时有极大值6e −1，则f(x)的极小值为( )A. 0B. −e −3C. −eD. −2e 36.甲、乙、丙、丁、戊五个人站成一排照相，若甲不站最中间的位置，则不同的排列方式有( )A. 48种B. 96种C. 108种D. 120种7.若王阿姨手工制作的工艺品每一件售出后可以获得纯利润4元，她每天能够售出的工艺品(单位：件)均值为50，方差为1.44，则王阿姨每天能够获得纯利润的标准差为( )A. 1.2B. 2.4C. 2.88D. 4.88.若样本空间Ω中的事件A 1，A 2，A 3满足P(A 1)=P(A 1|A 3)=14,P(A 2)=23,P(−A 2|A 3)=25,P(−A 2|−A 3)=16，则P(A 1−A 3)=( )A. 114B. 17C. 27D. 528二、多选题：本题共3小题，共18分。

文科数学试题 第1页（共16页） 文科数学试题 第2页（共16页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________2019-2020学年下学期期末测试卷高二文科数学（考试时间：120分钟 试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．测试范围：人教选修1-1、1-2、4-4、4-5。

5．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．设复数z 满足1z i -=，则z 最大值为（ ） A ．1B 2C ．2D ．42．命题“对任意x ∈R ，都有11x x-<”的否定是（ ） A ．对任意x ∈R ，都有11x x -≥ B ．不存在x ∈R ，使得11x x-< C ．存在x ∈R ，使得11x x -≥ D ．存在x ∈R ，使得11x x-> 3．设x ∈R ，则“|1|1x -<”是“220x x --<”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件4．用反证法证明“已知22,,0x y R x y ∈+=，求证：0x y ==.”时，应假设( ) A ．0x y ≠≠B ．0x y =≠C ．0x ≠且0y ≠D ．0x ≠或 0y ≠5．若t 为参数，则参数方程cos sin x t ay t bθθ=+⎧⎨=+⎩表示的点的轨迹为（ ）A ．直线B ．椭圆C ．圆D ．圆或直线6．点P 极坐标为5(2,)6π，则它的直角坐标是（ ） A ．(1,3)B ．(3)-C ．(3,1)-D ．(3,1)7．函数f (x )＝22x x -+ 在点 (1，2) 处的切线方程为（ ） A ．x +y +1=0B ．x -y -1=0C ．x -y +1=0D ．x +y -1=08．为研究某种细菌在特定环境下，随时间变化的繁殖情况，得到如下实验数据：天数x （天） 3 4 56 繁殖个数y （千个）2.5344.5由最小二乘法得y 与x 的线性回归方程为ˆˆ0.7yx a =+，则当7x =时，繁殖个数y 的预测值为（ ） A ．4.9 B ．5.25 C ．5.95 D ．6.15 9．点()5,3M 到抛物线2y ax =的准线的距离为6，则该抛物线的方程是（ ） A ．212y x =B ．236y x =-C ．212y x =或236y x =-D ．2112y x =或2136y x =- 10．如图所示的茎叶图为高三某班50名学生的化学考试成绩，算法框图中输入的1a ，2a ，3a ，，50a 为茎叶图中的学生成绩，则输出的m ，n 分别是（ ）A ．38m =，12n =B ．26m =，12n =C ．12m =，12n =D ．24m =，10n =11．已知双曲线22221(0,0)x y a b a b -=>>5则椭圆22221x y a b +=的离心率为( )文科数学试题 第3页（共16页） 文科数学试题 第4页（共16页）……○………………内………………○………………装………………○………………订………………○………………线………………○………………此卷只装订不密封……○………………外………………○………………装………………○………………订………………○………………线………………○………………A ．12B 3C 3D 212．已知函数()31sin f x x x x =+++，若()()2122f a f a -+≤，则实数a 的取值范围是( )A ．3[1,]2-B ．3[,1]2-C ．1[1]2-，D ．1[,1]2-第Ⅱ卷二、填空题（本题共4小题，每小题5分，共20分）13．若命题“∃t ∈R ，t 2-2t -a ＜0”是假命题，则实数a 的取值范围是 ______. 14．已知曲线ln y x =的切线过原点，则此切线的斜率为__________．15．若对任意的x ∈R ，不等式1221x x a --+≤-恒成立，则实数a 的取值范围为________.16．已知双曲线()22210x y a a-=>的一条渐近线方程为12y x =，则a =______；离心率e =______.三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分12分）已知0m >，p :(2)(6)0x x +-≤,q :22m x m -≤≤+ ． （I ）若p 是q 的充分条件，求实数m 的取值范围；（Ⅱ）若5m =，“p 或q ”为真命题，“p 且q ”为假命题，求实数x 的取值范围18．（本小题满分12分） 已知z 为虚数，42z z +-为实数． （1）若2z -为纯虚数，求虚数z ； （2）求|4|z -的取值范围．19．（本小题满分12分）2019年上半年我国多个省市暴发了“非洲猪瘟”疫情，生猪大量病死，存栏量急剧下降，一时间猪肉价格暴涨，其他肉类价格也跟着大幅上扬，严重影响了居民的生活.为了解决这个问题，我国政府一方面鼓励有条件的企业和散户防控疫情，扩大生产；另一方面积极向多个国家开放猪肉进口，扩大肉源，确保市场供给稳定.某大型生猪生产企业分析当前市场形势，决定响应政府号召，扩大生产，决策层调阅了该企业过去生产相关数据，就“一天中一头猪的平均成本与生猪存栏数量之间的关系”进行研究.现相关数据统计如下表：生猪存栏数量x （千头）2 3 4 5 8 头猪每天平均成本y （元）3.22.421.91.5（1）研究员甲根据以上数据认为y 与x 具有线性回归关系，请帮他求出y 关于x 的线性回归方程(1)ybx a =+（保留小数点后两位有效数字）（2）研究员乙根据以上数据得出y 与x 的回归模型：(2)4.80.8y x=+.为了评价两种模型的拟合结果，请完成以下任务：①完成下表（计算结果精确到0.01元）（备注：i e 称为相应于点(),i i x y 的残差）；生猪存栏数量x （千头） 2 3 4 5 8 头猪每天平均成本y （元）3.2 2.4 2 1.9 1.5 模型甲估计值(1)iy残差(1)ie模型乙估计值(2)iy 3.2 2.4 2 1.76 1.4残差(2)ie 0 0 0 0.14 0.1②分别计算模型甲与模型乙的残差平方和1Q 及2Q ，并通过比较1Q 与2Q 的大小，判断哪个模型拟合效果更好；（3）根据市场调查，生猪存栏数量达到1万头时，饲养一头猪每一天的平均收入为7.5元；生猪存栏数量达到1.2万头时，饲养一头猪每一天的平均收入为7.2元.若按（2）中拟合效果较好的模型计算一天中一头猪的平均成本，问该生猪存栏数量选择1万头还是1.2万头能获得更多利润?请说明理由.（利润=收入-成本）文科数学试题 第5页（共16页） 文科数学试题 第6页（共16页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________参考公式：()()()1122211n niii ii i nniii i x x y y x y nx yx x xnxb ∧====---==--∑∑∑∑，x y b a ∧∧∧=+参考数据：()()()255115.3,21.2iiii i x x y y x x ==--=--=∑∑.20．（本小题满分12分）已知抛物线()2:20C y px p =>经过点(2.（1）写出抛物线C 的标准方程及其准线方程，并求抛物线C 的焦点到准线的距离；（2）过点()2,0且斜率存在的直线l 与抛物线C 交于不同的两点A ，B ，且点B 关于x 轴的对称点为D ，直线AD 与x 轴交于点M . （i ）求点M 的坐标；（ii ）求OAM △与OAB 面积之和的最小值.21．已知函数()()ln a xf x x a R x=+∈. （1）若函数()f x 的图象在2x e =处的切线与y x =平行，求实数a 的值； （2）设()()()201,221a g x xf x x a x <≤=-+-.求证：()g x 至多有一个零点.请考生在第22、23两题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做的第一个题目文科数学试题 第7页（共16页） 文科数学试题 第8页（共16页）……○………………内………………○………………装………………○………………订………………○………………线………………○………………此卷只装订不密封……○………………外………………○………………装………………○………………订………………○………………线………………○………………计分．22．（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xoy 中，直线l 的参数方程为222212x t y t ⎧=-+⎪⎪⎨⎪=+⎪⎩（t 为参数）.再以原点为极点，以x 正半轴为极轴建立极坐标系，并使得它与直角坐标系xoy 有相同的长度单位.在该极坐标系中圆C 的方程为4sin ρθ=.（1）求圆C 的直角坐标方程；（2）设圆C 与直线l 交于点A 、B ，若点M 的坐标为()2,1-，求MA MB +的值.23．（本小题满分10分）选修4-5：不等式选讲设,,x y z ∈R ，且1x y z ++=. （1）证明：22213x y z ++≥； （2）求()()()222111x y z -++++的最小值.2019-2020学年下学期期末测试卷01高二文科数学·全解全析1 2 3 4 5 6 7 8 9 1011 12 C CADADCBDBCC1．【答案】C【解析】设z a bi =+，,a b ∈R ，1z i -=，∴()2211a b +-=即()2211a b +-=，∴点(),a b 在圆()2211x y +-=上，又该圆的圆心为()0,1，半径为1，∴该圆上所有点到原点的距离最大值为112+=，即22max2a b +=，∴max 2z =.2．【答案】C【解析】命题“对任意x ∈R ，都有11x x -<”的否定是：存在x ∈R ，使得11x x-≥， 3．【答案】A【解析】1111102x x x -<⇔-<-<⇔<<，22012x x x --<⇒-<<. 4．【答案】D【解析】根据反证法证明数学命题的方法，应先假设要证命题的否定成立，而0x y ==的否定为“,x y 不都为零”，故选D.文科数学试题 第9页（共16页） 文科数学试题 第10页（共16页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________5．【答案】A【解析】因为参数方程cos sin x t a y t b θθ=+⎧⎨=+⎩，则cos sin x a t y b t θθ-=⎧⎨-=⎩消参数t ，有：()sin ()cos x a y b θθ-=-，即sin cos cos sin 0x y b a θθθθ⋅-⋅+-=， 故轨迹为一条直线 6．【答案】D【解析】552cos 3,2sin 166x y ππ==-== ∴M 点的直角坐标是()3,1-7．【答案】C 【解析】()()2'2,21f x x x f x x =-+∴=-，()'12111f ∴=⨯-=.∴函数()f x 在点()1,2处的切线方程为21y x -=-，即10x y -+=. 8．【答案】B【解析】由题意，根据表格中的数据，可得34569 2.534 4.57,4242x y ++++++====，即样本中心为97(,)22，代入回归直线方程ˆˆ0.7yx a =+，即79ˆ0.722a =⨯+， 解得ˆ0.35a=，即回归直线的方程为ˆ0.70.35y x =+， 当7x =时，ˆ0.770.35 5.25y=⨯+=，故选B ． 9．【答案】D【解析】当0a >时，开口向上，准线方程为14y a =-，则点M 到准线的距离为1364a +=，求得112a =，抛物线方程为2112y x =， 当0a <时，开口向下，准线方程为14y a =-，点M 到准线的距离为1|3|64a +=解得136a =-，抛物线方程为2136y x =-． 10．【答案】B【解析】由程序框图可知，框图统计的是成绩不小于80和成绩不小于60且小于80的人数，由茎叶图可知，成绩不小于80的有12个，成绩不小于60且小于80的有26个，故26m =，12n =． 11．【答案】C【解析】由双曲线离心率得：22222514a b b a a +=+=，解得：224a b = ∴椭圆方程为222214x y b b += ∴椭圆离心率222434b b e b -== 12．【答案】C【解析】因为()31sin f x x x x =+++设()()31sin g x f x x x x =-=++，定义域x ∈R()()3sin g x x x x g x -=---=-，所以()g x 为奇函数， ()231cos 0g x x x '=++≥，所以()g x 单调递增， 不等式()()2122f a f a-+≤()()21121f a f a ⎡⎤--≤--⎣⎦()()212g g a a ≤-- ()()212g g a a ≤--2a 12a -≤-解得112x ≤≤- 13．【答案】(],1-∞-【解析】命题“∃t ∈R ，t 2-2t -a ＜0”是假命题， 等价于∀t ∈R ，t 2-2t -a≥0是真命题， ∴△=4+4a≤0，解得a≤-1． ∴实数a 的取值范围是（-∞，-1]．文科数学试题 第11页（共16页） 文科数学试题 第12页（共16页）……○………………内………………○………………装………………○………………订………………○………………线………………○………………此卷只装订不密封……○………………外………………○………………装………………○………………订………………○………………线………………○………………故答案为（-∞，-1]．14．【答案】1e【解析】y=lnx 的定义域为(0,+∞),设切点为(x 0,y 0),则1|x x k Y x ︒=︒='=,所以切线方为 y -y 0= 1x ︒(x -x 0),又切线过点(0,0),代入切线方程得y 0=1,则x 0=e,所以11|x x k Y x e︒=︒=='=. 15．【答案】(][)12-∞-⋃+∞，， 【解析】()()12123y x x x x =--+≤--+=，∴要使1221x x a --+≤-恒成立，则213a -≥，213a -≥或213a -≤-， 即2a ≥或1a ≤-，∴实数a 的取值范围是(][)12-∞-⋃+∞，，.故答案为(][)12-∞-⋃+∞，，.16．【答案】25【解析】由双曲线方程()22210x y a a -=>，可得其渐近线方程为1y x a =±，因为双曲线的一条渐近线方程为12y x =，所以2a =，又由2222215c a b =+=+ 所以双曲线的离心率为5c e a ==. 17．（本小题满分12分）【解析】（1）:26p x -≤≤，∵p 是q 的充分条件，∴[2,6]-是[2,2]m m -+的子集，0{22426m m m m >-≤-⇒≥+≥，∴m 的取值范围是[4,)+∞． (6分)（2）由题意可知,p q 一真一假，当5m =时，:37q x -≤≤，p 真q 假时，由26{37x x x x -≤≤⇒∈∅-或；p 假q 真时，由26{3237x x x x -⇒-≤<--≤≤或或67x <≤．所以实数x 的取值范围是[3,2)(6,7]--⋃．(12分) 18．（本小题满分12分）【解析】由于z 为虚数，可设(z x yi x =+，y R ∈，0)y ≠， （1）则22z x yi -=-+， 由2z -为纯虚数，得2x =， 2z yi ∴=+，又因为42z z +-为实数， 则(442)242z yi y i R z yi y +=++=+-∈-， 得40y y-=，2y =±， 所以22z i =+或22z i =-.(6分) （2）2222(4442)4[]22(2)(2)x y z x yi x y i R z x yi x y x y -+=++=++-∈-+--+-+， 因为42z z +-为实数，∴2240(2)y y x y -=-+， 0y ≠，22(2)4x y ∴-+=，224(2)0y x =-->∴，则2(2)4x -<，解得：(0,4)x ∈，∴2222|4||4|(4)(4)4(2)164z x yi x y x x x -=+--+-+---由于(0,4)x ∈，则016416x <-<，所以01644x <-， 即0|4|4z <-<，所以|4|z -的取值范围为()0,4.(12分) 19．（本小题满分12分）【解析】（1）由题知：()()()121ˆ 5.34.4, 2.2,0.2521.2ni i i n i i x x y y x y b x x ==---=====--∑∑， ˆˆ 2.20.25 4.4 3.30ay bx =-=+⨯=，故()10.2 3.0ˆ53y x =-+.(4分)文科数学试题 第13页（共16页） 文科数学试题 第14页（共16页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________（2）①经计算，可得下表： 生猪存栏数量x （千头） 2 3 4 5 8 头猪每天平均成本y （元）3.2 2.4 2 1.9 1.5 模型甲估计值()1ˆi y2.802.552.302.051.30残差()1ˆi e 0.40 -0.15 -0.30 -0.15 0.20模型乙估计值()2ˆi y3.22.421.761.4残差()2ˆi e0.140.1()()()()()2222210.400.150.300.150.20Q =+-+-+-+ ()()2220.140.1Q =+ 因为12Q Q >，故模型()2 4.8.8ˆ0yx=+的拟合效果更好. (4分) （3）若生猪存栏数量达到1万头，由（2）模型乙可知，每头猪的成本为4.80.8 1.2810+=元， 这样一天获得的总利润为()7.5 1.281000062200-⨯=元. 若生猪存栏数量达到1.2万头， 由（2）模型乙可知，每头猪的成本为4.80.8 1.212+=元， 一天获得的总利润为()7.2 1.21200072000-⨯=元，因为7200062200>，所以选择择生猪存栏数量1.2万头能获得更多利润. (4分) 20．（本小题满分12分）【解析】（1）由题意，抛物线()2:20C y px p =>经过点()1,2，即221(2)p ⨯=，解得1p =，所以抛物线的方程为22y x =，抛物线的准线方程为12x =-，抛物线的焦点到准线的距离为1. (4分)（2）（i ）设过点()2,0的直线:2l x my =+， 代入抛物线22y x =的方程，可得2240y my --=，设直线l 与抛物线C 的交点112222(,),(,),(,)A x y B x y D x y -，且10y >，则212122,4,4160y y m y y m +==-∆=+>，所以直线AD 的方程为121112()y y y y x x x x +-=--，即121112()()y y y y x x m y y +-=--，即11122()y y x x y y -=--，令0y =，可得()21211()2y y y x y -⋅-=-，所以21211122()()4x y y y y y y =-⋅-+==-，所以2x =-，所以(2,0)M -，(8分)（ii ）如图所示，可得11111222OAM S OM y y y ∆=⨯⋅=⨯⋅=， 1212112222OAB S y y y y ∆=⨯⨯+⨯⨯=+，所以OAM ∆与OAB ∆面积之和为：1212111422OAB OAM S y y y y S y y y ∆∆-++=+=++=11114422242y y y y =+≥⋅= 当且仅当1142y y =时，即12y 时等号成立， 所以OAM ∆与OAB ∆面积之和的最小值为42分)21．（本小题满分12分）【解析】（1）已知函数()()ln a xf x x a R x=+∈， 所以()()21ln 1a x f x x-'=+， 所以()()()222421ln 11a e af e e e -'=+=-+，文科数学试题 第15页（共16页） 文科数学试题 第16页（共16页）……○………………内………………○………………装………………○………………订………………○………………线………………○………………此卷只装订不密封……○………………外………………○………………装………………○………………订………………○………………线………………○………………因为函数()f x 的图象在2x e =处的切线与y x =平行，所以()2411af e e '=-+=， 解得0a =.(6分)（2）因为()()()()22221ln 21g x xf x x a x a x x a x =-+-=-+-，所以()()()()()222121221x a x a x x a ag x x a x x x---+-'=-+-=-=-， 当0,()0x a g x '<<>，当,()0x a g x '><， 所以当x a =时，()()max ln 1g x a a a =+-， 令ln 1t a a =+-， 所以110t a'=+>， 所以t 在()01a ∈，上是增函数.所以0t ≤，即()0g x ≤. 所以()g x 至多有一个零点. (12分)22．（本小题满分10分）选修4-4：坐标系与参数方程【解析】（1）由极坐标与直角坐标互化公式得 圆的直角坐标方程式为22(2)4x y +-=(5分)（2）直线l 参数方程222212x y ⎧=-+⎪⎪⎨⎪=+⎪⎩代入圆方程得：23210t t -+=设A 、B 对应的参数分别为1t 、2t ，则1232t t +=，121t t = 于是121232MA MB t t t t +=+=+=分) 23．（本小题满分10分）选修4-5：不等式选讲【解析】（1）证明：因为()()22222222223x y z x y z xy xz yz x y z++=+++++≤++，当且仅当13x y z ===时，等号成立， 又∵1x y z ++=，∴22213x y z ++≥；(5分) （2）由（1）知：()()()()22221411111133x y z x y z -++++≥-++++=， 当且仅当111x y z -=+=+且1x y z ++=即53x =、13y z ==-时，等号成立，所以()()()222111x y z -++++有最小值43.(10分)。

2023学年玉林市高二数学（下）期末质量监测试卷（试卷总分150分，考试时间120分钟）一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.集合{}2230A x x x =+-=，{1,3}B =，则A B = （）A.{}1 B.{3}C.{3,1,3}- D.{1,1,3}-2.下列说法中，正确的是（）A.若0a b >>，0c d <<，则一定有a b c d>B.若a b >，则11a b<C.若b a >，0m >，则a m ab m b+>+D.若22ac bc >，则a b>3.已知命题:[1,2]p x ∀∈，220x ax +->，则p 的一个必要不充分条件是（）A.1a <- B.0a > C.1a > D.2a >4.已知线性回归方程ˆˆ0.7ybx =+相应于点(2,6.6)的残差为0.1-，则ˆb 的值为（）A.3- B.3C. 2.9- D.2.95.中国古代儒家要求学生掌握六种基本才能（六艺）：礼、乐、射、御、书、数.某校国学社团周末开展“六艺”课程讲座活动，一天连排六节，每艺一节，则“射”与“数”之间间隔一艺的不同排课方法总数有（）A.432种B.240种C.192种D.96种6.我中有6个球，其中红黄蓝紫白黑球各一个，甲乙两人按序从袋中有放回的随机摸取一球，记事件A ：甲和乙至少一人摸到红球，事件B ：甲和乙摸到的球颜色不同，则条件概率()P B A =（）A.1011B.13C.56D.897.已知R 上的可导函数()f x 的函数图象如图所示，则不等式()0xf x '>的解集为（）A.(1,0)(1,)-+∞B.(,2)(1,2)-∞-C.(,1)(1,)-∞-+∞D.(1,1)(2,)-+∞ 8.中国南北朝时期的著作《孙子算经》中，对同余除法有较深的研究，对于两个整数a ，b ，若它们除以正整数m 所得的余数相同，则称a 和b 对模m 同余，记为)m d (o a b m ≡.若0122171717C C 6C 6a =+⨯+⨯+171717C 6⋯+⨯，(mod8)a b ≡，则b 的值可以是（）A.2021B.2022C.2023D.2024二、多项选择题：本题共3小题，每小题6分，共18分.每小题给出的选项中，有多项符合题目要求.全部选对得6分，部分选对得部分分，选错或不选得0分.9.下列函数中最小值为4的是（）A.4ln ln y x x=+B.4sin sin y x x=+C.222xxy -=+ D.2y =10.已知随机变是X 服从正态分布(0,1)N ，定义函数()f x 为X 取值不超过x 的概率，即()()f x P X x =≤，若0x ≥，则下列说法正确的有（）A.1(0)2f =B.(2)2()f x f x =C.()f x 在(0,)+∞上是增函数D.()()21P X x f x ≤=-11.若函数2()ln 2f x a x x bx =-+既有极小值又有极大值，则（）A.0b a< B.0b > C.2160b a +> D.4a b -<三、填空题：本题共3小题，每小题5分，共15分.12.甲、乙、丙、丁各自研究两个随机变量的数据，若甲、乙、丙、丁计算得到各自研究的两个随机变量的线性相关系数分别为10.96r =-，20.67r =，30.92r =，40.89r =，则这四人中，________研究的两个随机变量的线性相关程度最高.13.已知函数()2()ln 56f x x x =-++，则()f x 的定义域是________；单调增区间为________.14.已知函数()f x 是定义在R 上的偶函数，且(33)f x +为奇函数，记()f x '为()f x 的导函数，若(3)1f '=，则()y f x =在点(9,(9))f --处的切线一般式方程为________.四、解答题：本题共5小题，共77分.解答应写出必要的文字说明、证明过程或演算步骤.15.（13分）已知3()nx x-的展开式中共有10项.（1）求展开式中各项系数之和；（2）求展开式中的常数项，并确定有理项有多少项.16.（15分）2023年8月8日是我国第15个“全民健身日”，设立全民健身日（FitnessDay ）是适应人民群众体育的需求，促进全民健身运动开展的需要.某学校为了提高学生的身体素质，举行了跑步竞赛活动，活动分为长跑、短跑两类项目，该班级所有同学均参加活动，且男女同学人数比为2:1，每位同学选择一项活动参加.统计数据如下表：长跑短跑男同学a 10女同学1010（1）求α的值并依据小概率值0.01α=的独立性检验，能否推断选择跑步项目的类别与其性别相关；（2）赛后校记者团对参加长跑比赛的同学按性别采用分层随机抽样的方法抽取8名同学，再从这8名同学中抽取2名同学接受采访，记随机变量X 表示抽到的2人中女生的人数，求X 的布列与数学期望.附：22()()()()()n ad bc a b c d a c b d χ-=++++，其中n a b c d =+++.α0.050.010.001x α3.8416.63510.82817.（15分）已知函数21,10()2,0329,34x x f x x x x x x ⎧-≤<⎪⎪⎪=-≤≤⎨⎪-+<≤⎪⎪⎩（1）求()3f ，()4f ，()()1ff 的值;（2）()1f a =，求a 的值；（3）请在给定的坐标系中画出此函数的图象，并根据图象写出函数()f x 的值域（无需写出理由）.18.（17分）甲、乙两支队伍进行某项比赛，赛制分为两种，一种是五局三胜制，另一种是三局两胜制，根据以往数据，在决胜局（在五局三胜制中指的是第五局比赛，在三局两胜制中指的是第三局比赛）中，甲、乙两队获胜的概率均为12；而在非决胜局中，甲队获胜的概率为23，乙队获胜的概率为13.（1）若采用五局三胜制，直到比赛结束，共进行了Y 局比赛，求随机变量Y 的分布列，并指出进行几局比赛的可能性最大；（2）如果你是甲队的领队，你希望举办方采用五局三胜制还是三局两胜制？19.（17分）已知函数()ln(1)f x x =+与函数()2mxg x x=+的图象在0x =处的切线斜率相同.（1）求实数m 的值；（2）证明：当10x -<≤时，()()f x g x ≤；（3）设a 为正实数，讨论方程1()()02g x af x -=的解的个数.2024年春季期高二期末教学质量监测数学参考答案及解析一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.【解答】依题意，{3,1}A =-，而{1,3}B =，所以{3,1,3}A B =- .故选：C.2.【解答】对于A ，若2a =，1b =，2c =-，1d =-，则a bc d=，故A 错误.对于B ，若0a b >>，则110a b>>，故B 错误.对于C ，()()a m a mb a b m b b b m +--=++，若0b a >>，0m >，则()0()m b a b b m -<+，即a m ab m b +<+，所以C 错误.对于D ，由22ac bc >，可知20c ≠，即20c >，所以a b >，故D 正确.故选：D.3.【解答】因为[1,2]x ∀∈，220x ax +->，所以2a x x>-+在[]1,2上恒成立，只需2y x x =-+在[]1,2上的最大值小于a ，因为2y x x =-+在[]1,2上单调递减，故2y x x=-+在[]1,2上的最大值为1，所以1a >，A 选项既不是充分条件，也不是必要条件；B 选项因为10a a >⇒>所以0a >是p 的一个必要不充分条件.正确；C 选项1a >是p 的充要条件；D 因为21a a >⇒>，所以2a >是p 的充分不必要条件.故选：B.4.【解答】由线性回归方程ˆˆ0.7ybx =+，取2x =，得ˆˆ20.7y b =+，又相应于点(2,6.6)的残差为0.1-，ˆ6.620.70.1b∴--=-.解得ˆ3b =.故选：B.5.【解答】根据题意，“射”与“数”之间间隔一艺，有124424C A A 192=种排课方法.故选：C.6.【解答】袋中有6个球，其中红黄蓝白黑球各一个，甲乙两人按序从袋中有放回的随机摸取一球，记事件A ：甲和乙至少一人摸到红球，则事件A 的基本事件个数为665511⨯-⨯=，事件B ：甲和乙摸到的球颜色不同，则事件A B 的基本事件个数为11110-=，则10()11P B A =，故选：A.7.【解答】由函数()f x 的图象可得，当(,1)x ∈-∞-，(1,)+∞时，()0f x '>，当(1,1)x ∈-时，()0f x '<.由()0()00f x xf x x '>⎧'>⇔⎨>⎩①或()00f x x '<⎧⎨<⎩②解①得，1x >，解②得，10x -<<，综上，不等式()0xf x '>的解集为(1,0)(1,)-+∞ ，故选：A.8.【解答】已知01221717171717171717C C 6C 6C 6(16)7a =+⨯+⨯+⋯+⨯=+=则17017161161717(81)C 8C 8(1)1a =-=+⋯+⨯⨯--，即a 除以8所得的余数为7，显然2023除以8所得的余数为7，即b 的值可以是2023.故选：C.二、多项选择题：本题共3小题，每小题6分，共18分.每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对得部分分，选错或不选得0分.9.【解答】当ln 0x <时，A 显然错误；令sin t x =，则01t <≤，44y t t =+≥=，当且仅当2t =时取等号，B错误；2224x x y -=+≥=，当且仅当1x =时取等号，C 正确；0>，故24y ==+≥，当且仅当x =时取等号，D 正确.故选：CD.10.【解答】因为~(0,1)X N ，所以1(0)(0)2f P X =≤=，故A 正确；因为(2)(2)f x P X x =≤，2()2()f x P X x =≤，当0x >时，1()()2f x P X x =≤>，则2()1f x >，又(2)(2)1f x P X x =≤<，所以(2)2()f x f x =不成立，故B 错误；0x >，当x 增大时()()f x P X x =≤也增大，所以()f x 在(0,)+∞上是增函数，故C 正确；()()12()12[1()]2()1P X x P x X x P X x f x f x ≤=-≤≤=->=--=-，故D 正确.故选：ACD.11.【解答】24()4a x bx af x x b x x -++'=-+=，2()ln 2f x a x x bx =-+ 既有极小值又有极大值，240x bx a ∴-++=在(0,)+∞上有两个不同的实数根，21600404b a b a⎧⎪∆=+>⎪⎪∴>⎨⎪⎪->⎪⎩，216000b a b a ⎧+>⎪∴>⎨⎪<⎩，0ba∴<，0b >，2160b a +>，显然4a b -<不一定成立.故选：ABC.三、填空题：本题共3小题，每小题5分，共15分.12.【解答】因为13420.96r r r r =>>>，所以这四人中，甲研究的两个随机变量的线性相关程度最高.故答案为：甲.13.【解答】由2560x x -++>，解得16x -<<，则定义域是(1,6)-令256t x x =-++，其对称轴方程为52x =，图象是开口向下的抛物线，则256t x x =-++在51,2⎛⎤- ⎥⎝⎦上为增函数，又ln y t =为定义域内的增函数，则()f x 的单调增区间为51,2⎛⎤- ⎥⎝⎦.故答案为：(1,6)-；51,2⎛⎤- ⎥⎝⎦.（备注：单调增区间为51,2⎛⎫- ⎪⎝⎭也正确，答对第1个空得2分，第2个空得3分）14.【解答】因为()f x 是定义在R 上的偶函数，所以()()f x f x -=①，且(33)f x +为奇函数，(33)(33)f x f x -+=-+，所以(3)(3)f x f x -+=-+②，由①②可得()(6)f x f x =-+，即()f x 的周期为12，且(3)0f =，所以(9)(3)0f f -==，又()()f x f x ''--=，()(6)f x f x ''=-+，得(9)(96)(3)(3)1f f f f ''''-=--+=--==，所以()y f x =在点(9,(9))f --处的切线方程为：01(9)y x -=⨯+，即90x y -+=.故答案为：90x y -+=.四、解答题：本题共5小题，共77分.解答应写出必要的文字说明、证明过程或演算步骤.15.【解答】（1）由题意知9n =，在93x ⎫-⎪⎭的展开式中，令1x =.得：9(2)512-=-，因此93x ⎫-⎪⎭的展开式中，所有项的系数之和是512-（2）93x ⎫-⎪⎭展开式的通项：()9193r 1r 22199C 3C (3)(0,1,2,,9)rr rrr T x x xr ---+⎛⎫=-=-= ⎪⎝⎭令9302r-=，解得3r =，因此展开式中的常数项339C (3)2268-=-要使93329C (3)rrx--为有理项，则932rZ -∈，则1,3,5,7,9r =，故展开式中有理项有5项.16.【解答】（1）依题意男女同学人数的比例为2:1，所以1021010a +=+，故30a =，零假设0H ：选择跑步项目类别与学生性别无关，22(30101010)(30101010)15 3.75 6.635(3010)(1010)(3010)(1010)4χ+++⨯⨯-⨯===<+⨯+⨯+⨯+.根据小概率值0.01α=的独立性检验，没有充分证据推断出0H 不成立，因此可以认为0H 成立，即认为选择跑步项目类别与学生性别无关.（2）抽取8名同学中有6名男生，2名女生，则X 的所有可能取值为0，1，2，则206223C C 15(0)28C P X ===，116223C C 123(1)287C P X ====，026228C C 1(2)28C P X ===，则X 的分布列为：X 012P15283712815311()012.287282E X ∴=⨯+⨯+⨯=17.【解答】（1） 函数()21,102,0329,34x x f x x x x x x ⎧-≤<⎪⎪-≤≤⎨⎪-+<≤⎪⎩x x2(3)3233f ∴=-⨯=，(4)2491f =-⨯+=，(1)121f =-=-，1((1))(1)11f f f ∴=-==--.（2）①当0a <时，1()1f a a==，1a ∴=（舍去），②当03a ≤≤时，2()21f a a a =-=，解得1a =±又03a ≤≤，1a ∴=+，③当34a <≤时，()291f a a =-+=，4a ∴=，综上所述，a 的值为1 4.（3）函数()f x 的图象，如图：由图象可知，函数()f x 的值域为(],3-∞.18.【解答】（1）Y 的所有可能取值为3，4，5，33211(3)333P Y ⎛⎫⎛⎫==+= ⎪ ⎪⎝⎭⎝⎭，22223321212110(4)C C 33333327P Y ⎛⎫⎛⎫==⨯⨯⨯+⨯⨯⨯=⎪ ⎪⎝⎭⎝⎭，222421118(5)C 332227P Y ⎛⎫⎛⎫⎛⎫==⨯⨯⨯+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故Y 的分布列为：Y 345P131027827因为101827327>>，∴进行4局比赛的可能性最大.（2）采用三局两胜时，甲获胜概率()221322112C 133233P ⎛⎫=+-⨯⨯⨯= ⎪⎝⎭，采用五局三胜时，甲获胜概率()33223224422121120C 1C 33333227P ⎛⎫⎛⎫⎛⎫⎛⎫=+-⨯⨯+⨯⨯⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，21P P > ，∴如果我是甲队领队，采用五局三胜制.19.【解答】（1）1()1f x x '=+ ，22(2)2()(2)(2)m x mx mg x x x +-'==++，由题意可得，(0)(0)f g ''=，解得2m =；（2）证明：由（1）知，2()2xg x x =+，令2()()()ln(1)(10)2xx f x g x x x x ϕ=-=+--<≤+，则22214()01(2)(1)(2)x x x x x x ϕ'=-=≥++++，()x ϕ∴在其定义域(1,0)-内为单调递增函数，又(0)(0)(0)0f g ϕ=-=，时，()()()(0)0x f x g x ϕϕ=-≤=，即当10x -<≤时，()()f x g x ≤；（3）令1()()()ln(1)22xh x g x af x a x x =⋅-=-++，则定义域是(1,)-+∞，2222(24)(24)()1(2)(1)(2)a ax a x a h x x x x x -+-+-'=-=++++.令2(24)240ax a x a -+-+-=，4(12)a =-△（i ）当12a ≥时，0≤△，则()0h x '≤，()h x ∴在(1,)-+∞上单调递减，且(0)0h =，()h x ∴在(1,)-+∞上存在1个零点；（ii ）当102a <<时，0>△，设方程2(24)240ax a x a -+-+-=的两根分别为1x ，2x ，且12x x <，则121220x x a ⎛⎫+=->⎪⎝⎭，121220x x a ⎛⎫=-< ⎪⎝⎭，11所以()h x '有两个零点1x ，2x ，且1210x x -<<<，当()10,x x ∈时，()0h x '<，()h x 单调递减；当()12,x x x ∈时，()0h x '>，()h x 单调递增；当()2,x x ∈+∞时，()0h x '<，()h x 单调递减；故()()12(0)h x h h x <<，且(0)0h =，则()()120h x h x <<，又因为112101a a h e e --⎛⎫-=> ⎪⎝⎭+，112101a a h e e ⎛⎫--=< ⎪⎝⎭+，且111101e e αα--<-<<-，故有1112101a a e x x e --<<<<-，由零点存在性定理可知，()f x 在111,e x α-⎛⎫- ⎪⎝⎭恰有一个零点，在12,1x e α⎛⎫-⎪⎝⎭也恰有一个零点，易知0x =是()h x 的零点，所以()h x 恰有三个零点；综上所述，当12a ≥时，方程1()()02g x af x -=有1个解；当102a <<时，方程1()()02g x af x -=有3个解.。

郴州市2023-2024学年高二下学期期末教学质量监测数学（试题卷）注意事项：1.试卷分试题卷和答题卡.试卷共6页，有四大题，19小题，满分150分.考试时间120分钟.2.答卷前，考生务必将自己的姓名､准考证号填写在答题卡上，并将准者证条形码粘贴在答题卡的指定位置，3.考生作答时，选择题和非选择题均须作在答题卡上，在试题卷上作答无效考生在答题卡上按答题卡中注意事项的要求答题.4.考试结束后，将试题卷和答题卡一并交回.一､单项选择题（本大题共8小题，每小题5分，共40分，在所给的四个选项中，只有一个最佳答案，多选或不选得0分）1.设x ∈R ，则“3x >”是“2x >”的（ ）A.必要而不充分条件B.充分而不必要条件C.充要条件D.既不充分也不必要条件2.已知i 为虚数单位，若复数12,z z 在复平面内对应的点分别为()()2,1,1,2-，则复数12z z ⋅=（ ）A.5iB.5i -C.45i +D.45i-+1sin170=（ ）A.-4B.4C.-2D.24.已知P 为椭圆2222:1(0)x y C a b a b+=>>上一动点，12F F ､分别为其左右焦点，直线1PF 与C 的另一交点为2,A APF 的周长为16.若1PF 的最大值为6，则该椭圆的离心率为（ ）A.14 B.13 C.12 D.235.若n 为一组数8,2,4,9,3,10的第六十百分位数，则二项式1nx ⎫+⎪⎭的展开式的常数项是（ ）A.28B.56C.36D.406.三位老师和4名同学站一排毕业留影，要求老师们站在一起，则不同的站法有：（ ）A.360种B.540种C.720种D.900种7.已知函数()2(0,0)f x x bx c b c =-+>>的两个零点分别为12,x x ，若12,,2x x -三个数适当调整顺序后可为等差数列，也可为等比数列，则不等式0x bx c-≤-的解集为（ ）A.(](),45,∞∞-⋃+B.[]4,5C.()[),45,∞∞-⋃+D.(]4,58.设函数()f x 在R 上存在导数(),f x x '∀∈R ，有()()2f x f x x -+=，在()0,∞+上()f x x '<，若()()932262f m f m m --≥-，则实数m 的取值范围是（ ）A.1,4∞⎡⎫+⎪⎢⎣⎭B.1,2∞⎡⎫+⎪⎢⎣⎭C.[)1,∞+D.3,4∞⎡⎫+⎪⎢⎣⎭二､多项选择题（本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分）9.如图，正方体1111ABCD A B C D -的边长为2,M 为11A D 的中点，动点P 在正方形ABCD 内（包含边界）运动，且MP =.下列结论正确的是（ ）A.动点P 的轨迹长度为π；B.异面直线MP 与1BB 所成角的正切值为2；C.MP AB ⋅的最大值为2；D.三棱锥P MAD -的外接球表面积为25π4.10.已知定义域在R 上的函数()f x 满足：()1f x +是奇函数，且()()11f x f x -+=--，当[]()21,1,1x f x x ∈-=-，则下列结论正确的是（ ）A.()f x 的周期4T =B.5324f ⎛⎫=⎪⎝⎭C.()f x 在[]5,4--上单调递增D.()2f x +是偶函数11.锐角ABC 中，角,,A B C 的对边为,,a b c .且满足4,2a b c ==+.下列结论正确的是（）A.点A的轨迹的离心率e =3c <<C.ABC 的外接圆周长()4π,5πl ∈D.ABC 的面积()3,6ABC S ∈ 三､填空题（本题共3小题，每小题5分，共15分.）12.若直线:220l kx y k -+-=与曲线:C y =k 的取值范围是__________.13.已知数列{}n a 满足：()()111,11n n a na n a n n +=-+=+.若()1n nnb n a =+，则数列{}n b 的前n 项和n S =__________.14.暑假将临，大学生小明同学准备利用假期探访名胜古迹.已知某座山高䇯入人云，整体呈圆锥形，其半山腰（母线的中点）有一座古寺，与上山入口在同一条母线上，入口和古寺通过一条盘山步道相连，且当时为了节省资金，该条盘山步道是按“到达古寺的路程最短”修建的.如图，已知该座山的底面半径()2km R =，高)km h =，则盘山步道的长度为__________，其中上山（到山顶的直线距离减小）和下山（到山顶的直线距离增大）路段的长度之比为__________.（第一空2分，第二空3分）四､解答题（本大题共5小题，共77分）15.（本题满分13分）在锐角ABC 中，内角,,A B C 所对的边分别为,a b ，c ，且满足()sin cos sin 1cos c A B b C A =+.（1）证明：2A B =；（2）求ca的取值范围.16.（本题满分15分）如图，在四棱锥P ABCD -中，底面ABCD 为正方形，PA ⊥平面,2,ABCD PA AD E ==为线段PD 的中点，F 为线段PC （不含端点）上的动点.（1）证明：平面AEF ⊥平面PCD ；（2）是否存在点F ，使二面角P AF E --的大小为45 ？若存在，求出PFPC的值，若不存在，请说明理由.17.（本题满分15分）已知函数()2cos e ,xf x ax x a =+-∈R .（1）若()f x 在()0,∞+上单调递减，求实数a 的取值范围；（2）当0a =时，求证()1f x <在ππ,22x ⎛⎫∈- ⎪⎝⎭上恒成立.18.（本题满分17分）已知()2,A a 是抛物线2:2C y px =上一点，F 是抛物线的焦点，已知4AF =，（1）求抛物线的方程及a 的值；（2）当A 在第一象限时，O 为坐标原点，B 是抛物线上一点，且AOB 的面积为1，求点B 的坐标；（3）满足第（2）问的条件下的点中，设平行于OA 的两个点分别记为12,B B ，问抛物线的准线上是否存在一点P 使得，12PB PB ⊥.19.（本题满分17分）材料一：在伯努利试验中，记每次试验中事件A 发生的概率为p ，试验进行到事件A 第一次发生时停止，此时所进行的试验次数为ξ，其分布列为()()1(1)1,2,3,k P k p p k ξ-==-⋅=⋯，我们称ξ服从几何分布，记为()GE p ξ~.材料二：求无穷数列的所有项的和，如求2311111112222k k S ∞-==++++=∑ ，没有办法把所有项真的加完，可以先求数列前n 项和11112122nn k nk S -=⎛⎫==- ⎪⎝⎭∑，再求n ∞→时n S 的极限：1lim lim 2122n nn n S S →∞→∞⎛⎫==-= ⎪⎝⎭根据以上材料，我们重复抛掷一颗均匀的骰子，直到第一次出现“6点”时停止.设停止时抛掷骰子的次数为随机变量X.（1）证明：1()1k P X k∞===∑；（2）求随机变量X的数学期望()E X；（3）求随机变量X的方差()D X.郴州市2023-2024学年高二下学期期末教学质量监测数学参考答案和评分细则一､单项选择题（本大题共8小题，每小题5分，共40分，在所给的四个选项中，只有一个最佳答案，多选或不选得0分）1-5BABCA6-8CDD二､多项选择题（本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分）9.ACD 10.BC11.CD三､填空题（本题共3小题，每小题5分，共15分）12.10,2⎛⎤ ⎥⎝⎦13.1nn +14.5:2四､解答题（本大题共5小题，共77分）15.（本题满分13分）（1）由()sin cos sin 1cos c A B b C A =+，结合正弦定理得()sin sin cos sin sin 1cos ,sin 0C A B C B A C =+≠ 可得sin cos cos sin sin A B A B B -=，所以()sin sin A B B -=，所以A B B -=或()πA B B -+=（舍去），所以2A B=（2）在锐角ABC 中，02022032B A B C B ππππ⎧<<⎪⎪⎪<<<⎨⎪⎪<=-<⎪⎩，即ππ64B <<，cos B <<sin sin3sin2cos cos2sin 12cos sin sin2sin22cos c C B B B B B B a A B B B+====-.令1cos ,2,2B t y t t t ==-∈，因为122y t t =-在上单调递增，所以y y>=<=，所以ca∈.16.（1）证明： 底面ABCD为正方形，CD AD∴⊥.PA⊥平面,ABCD PA CD∴⊥.PA AD A⋂=CD∴⊥平面PAD.又AE⊂平面,PAD CD AE∴⊥.,PA PD E=为PD的中点，AE PD∴⊥.,CD PD D AE⋂=∴⊥平面PCD.AE⊂平面,AEF∴平面AEF⊥平面PCD.（2）以AB AD AP､､分别为x轴､y轴､z轴建立空间直角坐标系，()()0,0,0,2,0,0A B，()()()()2,2,0,0,2,0,0,0,2,0,1,1C D P E设(01)PF PCλλ=<<，()()2,2,22,0,1,1AF AP PF AP PC AEλλλλ=+=+=-=，设平面AEF的法向量()111,,m x y z=，则(),12,,m AEmm AFλλλ⎧⋅=⎪=--⎨⋅=⎪⎩()()2,2,0,0,0,2AC AP==，设平面APF的法向量()222,,n x y z=，则,n ACn AP⎧⋅=⎪⎨⋅=⎪⎩解得()1,1,0n=-由题意得：cos45m nm n⋅===，即13λ-=，解得23λ=.从而23PFPC=.17.（1）解：函数(),2cos e xf x ax x=+-，则()2sin e xf x a x=--'，对任意的()()0,,0x f x∞∈+'≤恒成立，所以()2e sinxa x g x≤+=，故()e cos1cos0xg x x x x=+≥++>'，所以()min 2()01a g x g ≤==，故实数a 的取值范围为1,2∞⎛⎤- ⎥⎝⎦；（2）证明：由题意知，要证在ππ,22x ⎛⎫∈-⎪⎝⎭，上，cos e 1x x -<，令()cos e xh x x =-，则()sin e xh x x =--'，显然在ππ,22x ⎛⎫∈-⎪⎝⎭上()h x '单调减，()π0,002h h ⎛⎫->< ⎪⎝⎭''，所以存在0π,02x ⎛⎫∈-⎪⎝⎭，则()000sin e 0x h x x '=--=，所以当0π,2x x ⎛⎫∈-⎪⎝⎭时，()0h x '>，则()h x 单调递增，当0π,2x x ⎛⎫∈ ⎪⎝⎭时，()0h x '<，则()h x 单调递减，所以()0max 00000π()cos ecos sin 04x h x h x x x x x ⎛⎫==-=+=+< ⎪⎝⎭，故()1f x <在ππ,22x ⎛⎫∈-⎪⎝⎭，上恒成立.18.解：（1）由题意242pAF =+=，解得4p =，因此抛物线的方程为2:8C y x =点()2,A a 在抛物线上可得216a =，故4a =±（2）设点B 的坐标为()11,,x y OA 边上的高为h ，我们知道AOB 的面积是：112S h =⨯=1h h =⇒==直线OA 的方程是2y x =，利用B 到直线OA 的距离公式可得：化简得：1121x y -=由于点B 在抛物线上，代入条件可得：22111121184y y y y ⋅-=⇒-=可以得到211440y y --=或211440y y -+=，解这个方程可以得到12y ===±12y =代入拋物线方程可以得到：1x ==或1x ==112x =综上所述，点B的坐标有三个可能的值：12312,2,,22B B B ⎛⎫+- ⎪⎝⎭（3）不存在，理由如下：由（2）知122,2B B +-则12,B B 的中点3,22M ⎛⎫⎪⎝⎭12B B ===M 到准线2x =-的距离等于37222+=因为73.52=>所以，以M 为圆心122B B 为半径的圆与准线相离，故不存在点P 满足题设条件.19.（1）证明：可知()()1151,1,2,3,666k X GE P X k k -⎛⎫⎛⎫~⋅==⋅=⋯ ⎪ ⎪⎝⎭⎝⎭012515151515115615666666666616nn nn S ⎛⎫- ⎪⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎝⎭=⋅+⋅+⋅+⋯+⋅=⨯=- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭-则15()lim lim 1 1.6n n n n k P X k S ∞→∞→∞=⎛⎫⎛⎫===-= ⎪ ⎪ ⎪⎝⎭⎝⎭∑.（2）设1()nn k T k P X k ==⋅=∑0121152535566666666n n -⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+⋯+⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭12151525155666666666n nn n n T --⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⋯+⨯+⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭两式相减，0121115151515566666666666n nn n T -⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+⋯+⨯-⨯ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭01215555555616666666n n n nn T n n -⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++⋯+-⨯=--⨯ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭则随机变量X 的数学期望55()lim lim 61666n nn n n E X T n →∞→∞⎛⎫⎛⎫⎛⎫⎛⎫==--⨯= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭；（3）1221151()(6)()lim (6)66k nn k k D X k P X k k -∞→∞==⎛⎫=-⋅==-⋅⋅⎪⎝⎭∑∑()2211111236()()(12)()36()k k k k k k P X k k P X k k P X k P X k ∞∞∞∞=====-+⋅===+-=+⋅=∑∑∑∑2211()12636()36;k k k P X k k P X k ∞∞====-⨯+==-∑∑【也可利用()()()22D XE XE X =-】而012122222151515151()123466666666n k k P X k n -∞=⎛⎫⎛⎫⎛⎫⎛⎫==+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∑ 121222215515151()12(1)6666666n k k P X k n -∞=⎛⎫⎛⎫⎛⎫⨯==+++-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑ 两式相减：012121151515151()135(21)666666666n k k P X k n -∞=⎛⎫⎛⎫⎛⎫⎛⎫==++++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∑ 112()()2()111k k k P X k P X k E X ∞∞===⋅=-==-=∑∑从而：21()66k kP X k ∞===∑.那么21()()3630k D X k P X k ∞===-=∑.。

石家庄市2023—2024学年度第一学期期末教学质量检测高二数学（本试卷满分150分，考试时间120分钟）注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上，写在本试卷上无效．3．考试结束后，将本试卷和答题卡一并交回．一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 某汽车启动阶段的位移函数为32()25s t t t =−，则汽车在2t =时的瞬时速度为（ ）A 10B. 14C. 4D. 62. 将序号分别为1，2，3，4，5的五张参观券全部分给甲，乙，丙，丁四人，每人至少1张，如果分给甲的两张参观券是连号，那么不同分法的种数是（ ） A. 6B. 24C. 60D. 1203. 设离散型随机变量X q =（ ）A.12B. 1C. 1D. 1±4. 已知一组观测值()11,x y ，()22,x y，…，(),n n x y 满足(1,2,)i i i y a bx e i n =++= ，若i e 恒为0，则2R =（ ） A. 0B. 0.5C. 0.9D. 15. (4的展开式中33x y 的系数为（ ）A. 4−B. 4C. 6−D. 66. 李老师教高二甲班和乙班两个班的数学，这两个班的人数相等．某次联考中，这两个班的数学成绩均近.似服从正态分布，其正态密度函数22()2()x f x µσ−=的图像如图所示，其中µ是正态分布的期望，σ是正态分布的标准差，且(||)0.6827P X µσ−≤=，(||2)0.9545P X µσ−≤=，(||3)0.9973P X µσ−≤=．关于这次数学考试成绩，下列结论正确的是（ ）A. 甲班的平均分比乙班的平均分高B. 相对于乙班，甲班学生的数学成绩更分散C. 甲班108分以上的人数约占该班总人数的4.55%D. 乙班112分以上的人数与甲班108分以上的人数大致相等7. 某校三位同学报名参加数理化生四科学科竞赛，每人限报且必须报两门，由于数学是该校优势科目，必须至少有两人参赛，若要求每门学科都有人报名，则不同参赛方案有（ ） A 51种B. 45种C. 48种D. 42种8. 已知函数()()31e 1xf x x kx =−−+，若对任意的()12,0,x x ∈+∞，且12x x ≠，都有()()()()11222112x f x x f x x f x x f x +>+，则实数k 的取值范围是（ ）A. e ,3∞−B. e ,3−∞C. 1,3 −∞D. 1,3−∞二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9. 下列说法中正确的是（ ）A. 对于独立性检验，2X 的值越大，说明两事件的相关程度越大B. 以模型e kx y c =去拟合一组数据时，为了求出回归方程，设ln z y =，将其变换后得到线性方程0.34z x =+，则,c k 的值分别是4e 和0.3C. 在具有线性相关关系的两个变量的统计数据所得的回归直线方程ˆˆˆy a bx =+中，ˆ2,1,3b x y ===，则ˆ1a= D. 通过回归直线ˆˆˆybx a =+及回归系数ˆb ，可以精确反映变量的取值和变化趋势 10. “杨辉三角”是中国古代数学文化的瑰宝之一，最早出现在南宋数学家杨辉于1261年所著的《详解九章的.算法》一书中．“杨辉三角”揭示了二项式系数在三角形数表中的一种几何排列规律，如图所示．下列关于“杨辉三角”的结论正确的是（ ）A. 222234511C C C C 220++++= B. 记第n 行的第i 个数为i a ，则11134n i n i i a +−==∑C. 第2023行中从左往右第1011个数与第1012个数相等D. 第30行中第12个数与第13个数之比为12∶1911. 某大学文学院有A B 、两个自习室，小王同学每天晩上都会去自习室学习.假设他第一天去自习室A 的概率为13；他第二天去自习室B 的概率为14；如果他第一天去自习室A ，则第二天去自习室B 的概率为12.下列说法正确的是（ ）A. 小王两天都去自习室A 的概率为14B. 小王两天都去自习室B 的概率为112C. 小王两天去不同自习室的概率为34D. 如果他第二天去自习室B ，则第一天去自习室A 的概率为12三、填空题：本题共3小题，每小题5分，共15分．12. 编号为1，2，3的三位学生随意入坐编号为1，2，3的三个座位，每位学生坐一个座位，设与座位编号相同的学生的个数是ξ，则()E ξ=__________．13. 在概率论中常用散度描述两个概率分布的差异.若离散型随机变量,X Y 的取值集合均为{}()*0,1,2,3,,n n ∈N，则,X Y 的散度()()()(||)ln ni P X i D X Y P X i P Y i =====∑.若X ，Y 的概率分布如下表所示，其中01p <<，则(||)D X Y 的取值范围是__________.14. 若二次函数()223f x x =+的图象与曲线C ：()e 3(0)xg x a a =+>存在公切线，则实数a 的取值范围是________.四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15. 设函数()32398f x x x x =−−+．（1）求f （x ）在1x =处的切线方程；（2）求f （x ）在[－2，4]上的最大值和最小值． 16. 已知()()23nf x x =−展开式的二项式系数和为512，且()()()()20122311nnn x a a x a x a x −=+−+++− ．（1）求2a 的值；（2）求123n a a a a ++++ 的值； （3）求12323n a a a na ++++ 的值．17. 在十余年的学习生活中，部分学生养成了上课转笔的习惯．某研究小组为研究转笔与学习成绩好差的关系，从全市若干所学校中随机抽取100名学生进行调查，其中有上课转笔习惯的有55人．经调查，得到这100名学生近期考试的分数的频率分布直方图．记分数在600分以上的为优秀，其余为合格．（1）请完成下列22×列联表．并依据小概率值0.01α=的独立性检验，分析成绩优秀与上课转笔之间是否有关联；（结果均保留到小数点后三位）上课转笔上课不转笔合计优秀合格20合计55100（2）现采取分层抽样的方法，从这100人中抽取10人，再从这10人中随机抽取5人进行进一步调查，记抽到5人中合格的人数为X ，求X 的分布列和数学期望；（3）若将频率视作概率，从全市所有在校学生中随机抽取20人进行调查，记20人中上课转笔的人数为k 的概率为()P k ，当()P k 取最大值时，求k 的值．附：22()()()()()n ad bc a b c d a c b d χ−=++++，其中n a b c d =+++．()2P k χ≥0.050 0.010 0.001 k3.8416.63510.82818. 一个调查学生记忆力的研究团队从某中学随机挑选100名学生进行记忆测试，通过讲解100个陌生单词后，相隔十分钟进行听写测试，间隔时间t （分钟）和答对人数y 的统计表格如下： 时间t （分钟） 102030405060708090100答对人数y987052363020151155lg y 1.99 1.85 1.72 1.56 1.48 1.30 1.18 1.04 0.7 07时间t 与答对人数y 和lg y 的散点图如下：附：102138500ii t==∑，101342i i y ==∑，101lg 13.52i i y ==∑，10110960i i i t y ==∑，101lg 621.7i i i t y ==∑，对于一组数据()11,u v ，()22,u v ，…，(),n n u v ，其回归直线方程ˆˆˆv u αβ=+的斜率和截距的最小二乘估计分别为：1221ˆni i i nii u v nu vunu β==−=−∑∑，ˆˆv u αβ=−．请根据表格数据回答下列问题： （1）根据散点图判断，yat b =+与lg y ct d =+哪个更适宜作为线性回归模型？（给出判断即可，不必说明理由）（2）根据（1）的判断结果，建立与t 的回归方程；（a ，b 或c ，d 的计算结果均保留到小数点后三位） （3）根据（2）请估算要想答对人数不少于75人，至多间隔多少分钟需要重新记忆一遍．（结果四舍五入保留整数）（参考数据：lg 20.3≈，lg 30.48≈）． 19. 对于正实数a ，()b a b >，我们熟知基本不等式：(,)(,)G a b A a b <，其中(,)G a b =为a ，b 几何平均数，(,)2a b A a b +=为a ，b 的算术平均数．现定义a ，b 的对数平均数：(,)ln ln abL a b a b −=−．（1）设1x >，求证：12ln x x x<−；（2）证明(,)(,)G a b L a b <；（3）若不等式(,)(,)(,)G a b A a b m L a b +>⋅对任意正实数,()a b a b >恒成立，求正实数m 的取值范围．.的。

卜人入州八九几市潮王学校HY 吴起高级二零二零—二零二壹高二数学下学期第四次质量检测〔期末考试〕试题理〔含解析〕第I 卷〔选择题一共60分〕一、单项选择题〔此题一共60分，每一小题5分，每个小题只有一个正确选项〕 1.设集合{}2|20A x xx =--≤，{}3|log 1B x x =≤，那么A B =〔〕A.[]1,2- B.(]0,1C.(]0,2D.[]1,3【答案】C 【解析】 【分析】先由二次不等式及对数不等式的解法求出集合A 、B ，然后结合集合交集的运算求A B 即可.【详解】解：解不等式220x x --≤，得12x -≤≤，即[]1,2A =-，解不等式3log 1x ≤，得03x <≤，即(]0,3B =，那么A B =(]0,2，应选：C.【点睛】此题考察了二次不等式及对数不等式的解法，重点考察了集合交集的运算，属根底题. 2.假设a 为实数，且()()12ai a i +-=，那么(a =)A.1-B.0C.1D.2【答案】C 【解析】直接利用复数代数形式的乘法运算化简得答案．【详解】解：∵a 为实数，且〔1+ai 〕〔a ﹣i 〕＝2a +〔a 2﹣1〕i ＝2， ∴2a ＝2且a 2﹣1=0，解得a ＝1． 应选C ．【点睛】此题考察了复数代数形式的乘除运算，是根底题．3.平面α，β，直线l 满足l α⊂，那么“//l β〞是“//αβ〞的〔〕A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】 【分析】利用定义法直接判断即可. 【详解】假设l α⊂，//l β不能推出//αβ，因为α与β可能相交；反过来，假设lα⊂，//αβ，那么l 与β无公一共点，根据线面平行的定义，知//l β.所以“//l β〞是“//αβ〞的必要不充分条件. 应选：B.【点睛】此题考察充分条件、必要条件的应用，在判断充分条件、必要条件时，有如下三种方法：1.定义法，2.等价法，3.集合间的包含关系法. 4.[]1,3x ∀∈-，2320x x -+≤〞的否认为〔〕 A.[]01,3x ∃∈-，200320x x -+>B.[]1,3x ∀∉-，2320x x -+> C.[]1,3x ∀∈-，2320x x -+>D.[]01,3x ∃∉-，200320x x -+>【解析】 【分析】 【详解】[]1,3x ∀∈-，2320x x -+≤〞的否认为“[]01,3x ∃∈-，20320x x -+>〞． 应选A ． 【点睛】5.假设532m mA A =，那么m 的值是() A.5 B.3 C.6 D.7【答案】A 【解析】 【分析】 根据题意，由532m m A A =，结合排列数公式可得m 〔m ﹣1〕〔m ﹣2〕〔m ﹣3〕〔m ﹣4〕=2×m〔m ﹣1〕〔m ﹣2〕，化简解可得答案． 【详解】根据题意，假设532m m A A =，那么有m 〔m ﹣1〕〔m ﹣2〕〔m ﹣3〕〔m ﹣4〕=2×m〔m ﹣1〕〔m ﹣2〕， 即〔m ﹣3〕〔m ﹣4〕=2， 解可得：m=5 故答案为A【点睛】(1)此题主要考察排列数的计算，意在考察学生对该知识的掌握程度和分析推理才能.(2)排列数公式：mnA =(1)(1)n n n m --+=()n n m -！！(n ，m ∈·N ，且m n ≤)．(1)(2)321!n n A n n n n =--⋅⋅⋅⋅⋅=(叫做n 的阶乘).6.甲、乙等5人排一排照相，要求甲、乙2人相邻但不排在两端，那么不同的排法一共有〔〕 A.36种 B.24种C.18种D.12种【答案】B 【解析】根据题意，甲、乙看做一个元素安排中间位置，一共有1222C A 4=种排法，其余3人排其它3个位置，一共有33A 6=种排法，利用乘法原理，可得不同的排法有4624⨯=种． 应选B ．点睛：此题考察的是排列组合问题.〔1〕解排列组合问题要遵循两个原那么：①按元素(或者位置)的性质进展分类；②按事情发生的过程进展分步．详细地说，解排列组合问题常以元素(或者位置)为主体，即先满足特殊元素(或者位置)，再考虑其他元素(或者位置)．〔2〕不同元素的分配问题，往往是先分组再分配．在分组时，通常有三种类型：①不均匀分组；②均匀分组；③局部均匀分组．注意各种分组类型中，不同分组方法的求解．7.=⎰〔〕A.πB.2πC.0D.4π 【答案】D 【解析】 【分析】定积分⎰的几何意义是圆221x y +=的14个圆的面积，计算可得结果.【详解】定积分0⎰的几何意义是圆221x y +=的14个圆的面积,∴101144=⨯=⎰ππ，应选D. 【点睛】此题考察定积分，利用定积分的几何意义是解决问题的关键，属根底题8.以下求导数运算正确的有()A.()sin 'cos x x =-B.211'x x⎛⎫=⎪⎝⎭ C.31log '3ln x xD.()1ln 'x x=【答案】D 【解析】 【分析】分别计算各选项的导数，判断即可.【详解】因为()sin 'cos x x =，故A 错误；因为211'x x ⎛⎫=- ⎪⎝⎭，故B 错误；因为31log 'ln 3x x ，故C 错误；D 正确. 应选：D.【点睛】此题考察根本初等函数的计算，需要熟记公式.9.函数()f x 在0x x =处的导数为()f x '，那么()()000lim x f x m x f x x∆→-∆-=∆等于〔〕A.()0mf x 'B.()0mf x '-C.()01f x m'-D.()01f x m' 【答案】B 【解析】 【分析】利用导数的定义即可求出．【详解】()()()()()0000000limlim x m x f x m x f x f x m x f x m mf x x m x∆→-∆→-∆--∆-'=-=-∆-∆应选：B ．【点睛】此题主要考察导数的定义的应用，属于根底题．10.p ：函数22y x x =-的单调递增区间是[1,)+∞q ：函数1y x x=-的单调递增区间是[1,)+∞，那么〔〕 A.p q ∧p q ∨C.p ⌝q ⌝【答案】D 【解析】 【分析】p 为真，利用增+q【详解】p ：函数22y x x =-的对称轴为1x =，且开口向上，所以在[1,)+∞p 为真；q ：函数1y x x =-的定义域为{|0}x x ≠，且y x =和1y x=-为增函数，所以函数1y x x =-的增区间为(,0)-∞和(0,)+∞q 所以q ⌝ 应选D. 【点睛】.11.甲乙丙三位老师分别在、、的三所里教授语文、数学、英语，： ①甲不在工作，乙不在工作； ②在工作的老师不教英语学科； ③在工作的老师教语文学科；④乙不教数学学科.可以判断乙工作的地方和教的学科分别是〔〕 A.，语文 B.，英语C.，数学D.，数学【答案】B 【解析】【分析】根据条件，进展合情推理，即可容易判断和选择.【详解】在工作的老师不教英语学科，故工作的老师教语文或者数学； 又在工作的老师教语文学科，故工作的老师教数学.综上，在的老师教数学，在工作的老师教语文，在工作的老师教英语； 又乙不教数学学科，故乙在或者工作；又甲不在工作，乙不在工作，故乙在工作，甲在工作，丙在工作. 综上所述：乙在教英语. 应选：B .【点睛】此题考察合情推理，注意认真审题即可，属简单题. 12.假设()fx lnx =与()2g x x ax =+两个函数的图象有一条与直线y x =平行的公一共切线，那么a =〔〕A.1B.2C.3D.3或者1-【答案】D 【解析】 【分析】 先根据和曲线()ln f x x =相切得到切线方程，再根据和二次函数相切得到参数值.【详解】设在函数()ln f x x =处的切点设为〔x,y 〕,根据导数的几何意义得到111k x x==⇒=，故切点为〔1，0〕，可求出切线方程为y=x-1,直线和()2g x x ax =+也相切，故21x ax x +=-,化简得到()2110xa x +-+=,只需要满足()21401 3.a a ∆=--=⇒=-或故答案为D.【点睛】求切线方程的方法：①求曲线在点P 处的切线，那么说明P 点是切点，只需求出函数在点P 处的导数，然后利用点斜式写出切线方程；②求曲线过点P 的切线，那么P 点不一定是切点，应先设出切点坐标，然后列出切点坐标的方程解出切点坐标，进而写出切线方程.第II 卷〔非选择题一共90分)二、填空题〔此题一共20分，每一小题5分〕 13.2,10x R x ax ∃∈-+<a 的取值范围是_______【答案】[]22-,【解析】 所以240a =-≤，解得22a -≤≤.答案为：[]2,2-.14.假设(12)nx -的展开式中，奇数项的二项式系数之和为32，那么该二项展开式的中间项为________． 【答案】3160x - 【解析】 【分析】先由奇数项的二项式系数之和为32确定n 值，从而根据二项展开式通项公式求出第4项即可. 【详解】解：(12)nx -的展开式中，奇数项的二项式系数之和为1232n -=，解得6n =，那么二项展开式一共7项，第4项为中间项，即()334636021x T C x =--=，故答案为:3160x -.【点睛】此题考察了二项式定理.此题的关键是结合条件求出n .求二项展开式有关问题的常见类型及解题策略：(1)求展开式中的特定项.可根据条件写出第r ＋1项，再由特定项的特点求出r 值即可.(2)展开式的某项，求特定项的系数.可由某项得出参数项，再由通项写出第r ＋1项，由特定项得出r 值，最后求出其参数.15.()2231x dx m -=⎰，那么()211mx x x ⎛⎫-+ ⎪⎝⎭的展开式中4x 的系数是________.【答案】20- 【解析】 【分析】计算定积分得出m 的值，再利用二项式定理求出21mx x ⎛⎫+ ⎪⎝⎭的展开式中含3x 和4x 的系数，得出答案.【详解】()()223200316m x dx x x =-=-=⎰，∴621x x ⎛⎫+ ⎪⎝⎭的通项为62361661rrrr r rT C xC xx，令363r -=得3r=，∴621x x ⎛⎫+ ⎪⎝⎭的展开式中含3x 的系数为3620C =，令364r得103r =， ∴621x x ⎛⎫+ ⎪⎝⎭的展开式中不含4x 项， ()211mx x x ⎛⎫∴-+ ⎪⎝⎭的展开式中4x 的系数为12020.故答案：20-.【点睛】此题考察的是定积分和二项式定理的运用，此题中根据定积分求出m 的值是关键，此题应注意展开式中含有4x 的式子有两种情况，属于简单题. 16.①假设复数z 满足1R z∈，那么z R ∈； ②假设复数z 满足2z ∈R ，那么z R ∈； ③假设复数12,z z 满足12z z R ∈，那么12z z =；④假设复数z R ∈，那么z R ∈． ________________. 【答案】①④ 【解析】 【分析】由复数的运算法那么，逐项判断即可.【详解】①设(),z a bi a b R =+∈，所以()()2211a bi a bi z a bi a bi a bi a b --===++-+，假设1R z∈，那么0b =，所以z a R =∈，所以①正确；②设(),za bi ab R =+∈，那么()2222z a b abi =-+，假设2z R ∈，那么0ab =，所以0a =或者0b =，因此(),z a bi a b R =+∈不一定为实数，所以②错误；③设()12,,,z a bi z c di a b c d R ，=+=+∈，那么()()()()12z z a bi c di ac bd ad bc i =++=-++，假设12z z R ∈，那么0ad bc +=；又2z c di =-，假设12z z =，那么a c =且b d =-，所以由0ad bc +=不一定能推出a c =且b d =-，因此③错误； ④设(),za bi ab R =+∈，那么z a bi =-，假设z R ∈，那么0b =，因此z R ∈，所以④正确.故答案为①④【点睛】此题主要考察复数的运算以及复数的概念，熟记概念和运算法那么即可，属于常考题型. 三、解答题(此题一共70分，17-21每一小题12分，22题10分) 17.集合(){}2|log 33A x x =+≤，{}|213B x m x m =-<≤+.〔1〕假设3m =，那么A B ；〔2〕假设A B B =，务实数m 的取值范围.【答案】〔1〕{}|36x x -<≤；〔2〕[][)1,24,-+∞【解析】 【分析】〔1〕将3m =代入可得集合B ，解对数不等式可得集合A ，由并集运算即可得解. 〔2〕由A B B =可知B 为A 的子集，即B A ⊆；当B =∅符合题意，当B 不为空集时，由不等式关系即可求得m 的取值范围. 【详解】〔1〕假设3m =，那么{}|56B x x =<≤，依题意(){}(){}222|log 33|log 3log 8A x x x x =+≤=+≤{}|35x x =-<≤，故{}|36A B x x =-<≤；〔2〕因为A B B =，故B A ⊆；假设213m m -≥+，即4m ≥时，B =∅，符合题意；假设213m m -<+，即4m <时，21335m m -≥-⎧⎨+≤⎩，解得12m -≤≤；综上所述，实数m 的取值范围为[][)1,24,-+∞.【点睛】此题考察了集合的并集运算，由集合的包含关系求参数的取值范围，注意讨论集合是否为空集的情况，属于根底题.18.现有10道题，其中6道甲类题，4道乙类题，张同学从中任取3道题解答. 〔I 〕求张同学至少取到1道乙类题的概率；〔II 〕所取的3道题中有2道甲类题，1道乙类题.设张同学答对甲类题的概率都是35，答对每道乙类题的概率都是45，且各题答对与否互相HY.用X 表示张同学答对题的个数，求X的分布列和数学期望.【答案】〔I 〕56〔II 〕见解析【解析】 【分析】〔I〕从10道试题中取出3个的所有可能结果数有310C，张同学至少取到1道乙类题的对立事件是：张同学取到的全为甲类题，代入古典概率的求解公式即可求解〔II〕先判断随机变量X的所有可能取值为0，1，2，3，根据题意求出随机变量的各个取值的概率，即可求解分布列及期望值【详解】解：()I设事件A=“张同学至少取到1道乙类题〞那么A=张同学至少取到的全为甲类题P∴〔A〕363105 1()16CP AC=-=-=()II X的所有可能取值为0，1，2，3 X的分布列为【点睛】此题主要考察了古典概型及计算公式，互斥事件、离散型随机变量的分布列及期望值的求解，考察了运用概率知识解决实际问题的才能．19.如下列图的多面体是由底面为ABCD的长方体被截面1AEC F所截面而得到的，其中14,2,3,1AB BC CC BE====〔1〕求BF的长；〔2〕求点C到平面1AEC F的间隔.【答案】〔1〕〔2〕11【解析】【分析】以D 为坐标原点，分别以DA DC DF 、、为x y z 、、轴，建立空间直角坐标系O xyz ， 〔1〕由1AEC F 为平行四边形，运用向量的模的计算方法，可得BF 的长度；〔2〕运用向量坐标运算计算点到平面的间隔．【详解】(1)建立如下列图的空间直角坐标系，那么D(0，0，0)，B(2，4，0)，A(2，0，0)，C(0，4，0)，E(2，4，1)，C 1(0，4，3)．设F(0，0，z)．∵AEC 1F 为平行四边形，∴由AEC 1F 为平行四边形，∴由=得，(-2，0，z)=(-2，0，2)，∴z=2．∴F(0，0，2)．∴=(-2，-4，2，于是||=2，即BF 的长为2；(2)设为平面AEC 1F 的法向量，显然不垂直于平面ADF ，故可设=(x ，y ，1)．⇒，即，∴又=(0，0，3)，设与的夹角为a ，那么cosα==，∴C 到平面AEC 1F 的间隔为d=||cosα=3×=．【点睛】本小题主要考察空间中的线面关系、点到面的间隔等根本知识，同时考察空间想象才能和推理、运算才能．20.某高校一共有学生15000人，其中男生10500人，女生4500人．为调查该校学生每周平均体育运动时间是的情况，采用分层抽样的方法，搜集300位学生每周平均体育运动时间是的样本数据(单位：小时)． 〔1〕应搜集多少位女生的样本数据？〔2〕根据这300个样本数据，得到学生每周平均体育运动时间是的频率分布直方图〔如下列图〕，其中样本数据的分组区间为：[0,2]，(2,4]，(4,6]，(6,8]，(8,10]，(10,12]．估计该校学生每周平均体育运动时间是超过4小时的概率；〔3〕在样本数据中，有60位女生的每周平均体育运动时间是超过4小时，请完成每周平均体育运动时间是与性别列联表，并判断能否在犯错误的概率不超过的前提下认为“该校学生的每周平均体育运动时间是与性别有关〞．附：K 2＝2()()()()()n ad bc a b c d a c b d -++++【答案】〔1〕90；〔2〕；〔3〕能在犯错误的概率不超过的前提下认为“该校学生的每周平均体育运动时间是与性别有关〞． 【解析】 【分析】〔1〕由分层抽样性质，得到45003009015000⨯=；〔2〕由频率分布直方图得()120.10.0250.75-+=；〔3〕利用2×2列联表求2K . 【详解】〔1〕由45003009015000⨯=，所以应搜集90位女生的样本数据；〔2〕由频率发布直方图得()120.10.0250.75-+=，该校学生每周平均体育运动时间是超过4小时的概率为；〔3〕由〔2〕知，300位学生中有300×0.75=225人的每周平均体育运动时间是超过4小时，75人平均体育运动时间是不超过4小时，又因为样本数据中有210份是关于男生的，90份是关于女生的，所以平均体育运动时间是与性别列联表如下： 每周平均体育运动时间是与性别列联表结合列联表可算得()22300456030165 4.762 3.8417522521090K ⨯⨯-⨯=≈>⨯⨯⨯，所以能在犯错误的概率不超过的前提下认为“该校学生的每周平均体育运动时间是与性别有关〞． 【点睛】利用频率分布直方图求众数、中位数与平均数时，易出错，应注意区分这三者，在频率分布直方图中：(1)最高的小长方形底边中点的横坐标即是众数； (2)中位数左边和右边的小长方形的面积和是相等的；(3)平均数是频率分布直方图的“重心〞，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和． 21.函数()()32f x ax x a R =+∈在43x =-处获得极值． ()1确定a 的值；()2假设()()x g x f x e =，讨论()g x 的单调性．【答案】〔1〕1.2a = 〔2〕()gx 在(),4-∞-和()1,0-内为减函数，在()4,1--和()0,+∞内为增函数．【解析】 〔1〕对()f x 求导得()232f x ax x '=+，因为()f x 在43x =-处获得极值，所以403f ⎛⎫-= ⎪⎝⎭'， 即1641683209333a a ⎛⎫⨯+⨯-=-= ⎪⎝⎭，解得12a =； 〔2〕由〔1〕得，()3212x gx x x e ⎛⎫=+⎪⎝⎭， 故()232323115222222x x x g x x x e x x e x x x e ⎛⎫⎛⎫⎛⎫=+++=++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭'()()1142x x x x e =++， 令()0g x '=，解得0,1x x ==-或者4x =-，当4x <-时，()0g x '<，故()g x 为减函数，当41x -<<-时，()0g x '>，故()g x 为增函数， 当10x -<<时，()0g x '<，故()g x 为减函数，当0x>时，()0g x '>，故()g x 为增函数，综上所知：(),4-∞-和()1,0-是函数()g x 单调减区间，()4,1--和()0,+∞是函数()g x 的单调增区间.22.曲线C 的极坐标方程为2sin cos 10ρθρθ+=，将曲线1cos :{sin x C y θθ==，〔α为参数〕，经过伸缩变换3{2x xy y='='后得到曲线2C ．〔1〕求曲线2C 的参数方程；〔2〕假设点M 的在曲线2C 上运动，试求出M 到曲线C 的间隔的最小值．【答案】〔1〕3cos {2sin x y θθ==〔θ为参数〕；〔2〕【解析】试题分析：〔1〕1cos :{sin x C y θθ==变换为2cos 3:{sin 2x C y θθ''==，即3cos {2sin x y θθ==〔θ为参数〕；〔2〕曲线C 化为直角坐标方程：2100y x +-=，利用点到直线的间隔公式，有3cos 4sin 1055d θθ+-==.试题解析：〔1〕将曲线〔α为参数〕，化为221x y +=，由伸缩变换3{2x x y y ='='化为13{12x x y y ='='， 代入圆的方程211132x y ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭''，得到()()222:194x y C +'='， 可得参数方程为3cos {2sin x y αα==；〔2〕曲线C 的极坐标方程2sin cos 10ρθρθ+=，化为直角坐标方程：2100y x +-=，点M 到C 的间隔()5sin 103cos 4sin 105555d θϕθθ--+-==≥= 点M 到C 的间隔的最小值为5考点：坐标系与参数方程．。

2021-2021学年高二数学下学期期末考试试题 理〔含解析〕制卷人：打自企； 成别使； 而都那。

审核人：众闪壹； 春壹阑； 各厅…… 日期：2022年二月八日。

一、选择题〔在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的〕 1.i 是虚数单位，那么12ii-的虚部是〔 〕 A. -2 B. -1C. i -D. 2i -【答案】B 【解析】 【分析】根据复数的除法运算把复数化为代数形式后可得其虚部．【详解】由题意得221222i i i i i i--==--，所以复数12ii-的虚部是1-． 应选B ．【点睛】此题考察复数的运算和复数的根本概念，解答此题时容易出现的错误是认为复数z a bi =+的虚部为bi ，对此要强化对根本概念的理解和掌握，属于根底题．2.用反证法证明“方程()200++=≠ax bx c a 至多有两个解〞的假设中，正确的选项是〔 〕A. 至少有两个解B. 有且只有两个解C. 至少有三个解D. 至多有一个解【答案】C 【解析】分析：把要证的结论进展否认，得到要证的结论的反面，即为所求． 详解：由于用反证法证明数学命题时，应先假设命题的否认成立，命题：“方程ax 2+bx+c=0〔a≠0〕至多有两个解〞的否认是：“至少有三个解〞， 应选：C ．点睛：此题主要考察用命题的否认，反证法证明数学命题的方法和步骤，把要证的结论进展否认，得到要证的结论的反面，是解题的打破口，属于中档题．()f x 的导函数为'()f x ，且满足2()'(2)ln f x x f x =+，那么'(2)f 的值是〔 〕A. 6B. 7C. 8D. 9【答案】C 【解析】 【分析】求出''1()2(2)f x x f x=+⋅，再把2x =代入式子，得到'(2)8f =. 【详解】因为''1()2(2)f x x f x =+⋅，所以'''1(2)4(2)(2)82f f f =+⋅⇒=.选C.【点睛】此题考察对'(2)f 的理解，它是一个常数，通过构造关于'(2)f 的方程，求得'(2)f 的值.4.甲、乙、丙、丁四位同学各自对A 、B 两变量的线性相关性做试验，并用回归分析方法分别求得相关系数r 与残差平方和m 如表：那么哪位同学的试验结果表达A 、B 两变量有更强的线性相关性〔 〕A. 甲B. 乙C. 丙D. 丁【答案】D 【解析】试题分析：由题表格；相关系数越大，那么相关性越强。

绵阳市开元中学高2013级高二（下）数学期末复习高二数学下学期期末复习检测题4（满分100分，45分钟完卷）制卷：王小凤 学生姓名一．选择题（本题共6个小题，每小题10分，共60分）1．（2012四川卷）7(1)x +的展开式中2x 的系数是（ ）A ．42B ．35C ．28D ．21 2．（2012四川卷）复数2(1)2i i-=（ ）A ．1B ．1-C ．iD ．i - 3．（2012四川卷）函数1(0,1)xy a a a a=->≠的图象可能是（ ）4．（2012四川卷）设a 、b 都是非零向量，下列条件中，使||||aba b =成立的充分条件是（ ） A ．a b =- B ．//a b C ．2a b = D ．//a b 且||||a b =5．（2012山东卷）现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张，从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张，不同取法的种数为（ ） A ．232 B ．252 C ．472 D ．4846．（2012全国卷）已知正四棱柱1111ABC D A B C D -中 ，2A B =，1CC =E 为1C C 的中点，则直线1AC 与平面BED 的距离为（ ）A ．2 B． CD ．1二、填空题：（本题共2小题，每小题5分，共10分）7．（2012四川）如图，在正方体1111ABC D A B C D -中，M 、N 分别是C D 、1C C 的中点，则异面直线1A M 与D N 所成角的大小是____________8．（2012新课标）已知向量a 、b 夹角为45︒，且1a =，2a b -= 则b =_________三、解答题（本题共3个小题，每小题15分，共30分）9．（2012四川） 某居民小区有两个相互独立的安全防范系统（简称系统）A 和B ，系统A 和B 在任意时刻发生故障的概率分别为110和p 。