湖北省钟祥市第一中学2016届高三数学5月适应性考试试题(一)文

2016届高三上学期第一次月考数学（文）试题Word版含答案2016届高三上学期第一次月考数学文试卷考试时间120分钟，满分150分一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合M ＝{x |x ≥0，x ∈R }，N ＝{x |x 2<1，x ∈R }，则M ∩N 等于( ) A ．[0,1] B ．[0,1) C ．(0,1]D ．(0,1)2．已知集合A ＝{1,2}，B ＝{1，a ，b }，则“a ＝2”是“A ?B ”的( ) A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．已知命题p ：所有有理数都是实数；命题q ：正数的对数都是负数，则下列命题中为真命题的是( ) A ．﹁p 或q B ．p 且q C ．﹁p 且﹁qD ．﹁p 或﹁q4．设函数f (x )＝x 2＋1，x ≤1，2x ，x >1，则f (f (3))等于( )A.15B ．3C.23D.1395．函数f (x )＝log 12(x 2－4)的单调递增区间是( )A ．(0，＋∞)B ．(－∞，0)C ．(2，＋∞)D ．(－∞，－2)6．已知函数f (x )为奇函数，且当x >0时，f (x )＝x 2＋1x ，则f (－1)等于( )A ．－2B ．0C ．1D ．27. 如果函数f (x )＝x 2－ax －3在区间(－∞，4]上单调递减，则实数a 满足的条件是( ) A ．a ≥8 B ．a ≤8 C ．a ≥4D ．a ≥－48. 函数f (x )＝a x －2＋1(a >0且a ≠1)的图像必经过点( ) A ．(0,1) B ．(1,1) C ．(2,0)D ．(2,2)9. 函数f (x )＝lg(|x |－1)的大致图像是( )10. 函数f (x )＝2x ＋3x 的零点所在的一个区间是( ) A ．(－2，－1) B ．(－1,0) C ．(0,1)D ．(1,2)11. 设f (x )＝x ln x ，若f ′(x 0)＝2，则x 0的值为( ) A ．e 2B ．eC.ln22D ．ln212. 函数f (x )的定义域是R ，f (0)＝2，对任意x ∈R ，f (x )＋f ′(x )>1，则不等式e x ·f (x )>e x ＋1的解集为( )．A ．{x |x >0}B ．{x |x <0}C ．{x |x <－1或x >1}D ．{x |x <－1或0<1}<="" p="">二、填空题：本大题共4小题，每题5分．13. 已知函数y ＝f (x )及其导函数y ＝f ′(x )的图像如图所示，则曲线y ＝f (x )在点P 处的切线方程是__________．14. 若函数f (x )＝x 2＋ax ＋b 的两个零点是－2和3，则不等式af (－2x )>0的解集是________． 15. 函数y ＝12x 2－ln x 的单调递减区间为________．16. 若方程4－x 2＝k (x －2)＋3有两个不等的实根，则k 的取值范围是________．三、解答题：解答应写出文字说明、证明过程或演算步骤17.(10分) 化简：(1)3131421413223b a b a ab b a -(a >0，b >0)；(2)(－278)23-＋(0.002)12-－10(5－2)－1＋(2－3)0.18．(12分)已知函数f (x )＝1a －1(a >0，x >0)，(1)求证(用单调性的定义证明)：f (x )在(0，＋∞)上是增函数； (2)若f (x )在[12，2]上的值域是[12，2]，求a 的值．19．（12分）已知定义在R 上的奇函数f (x )有最小正周期2，且当x ∈(0,1)时，f (x )＝2x4x ＋1.(1)求f (1)和f (－1)的值； (2)求f (x )在[－1,1]上的解析式．20．（12分）已知函数f (x )＝x 2＋2ax ＋3，x ∈[－4,6]． (1)当a ＝－2时，求f (x )的最值；(2)求实数a 的取值范围，使y ＝f (x )在区间[－4,6]上是单调函数；(3)当a ＝1时，求f (|x |)的单调区间． 21．（12分）已知函数f (x )＝x 3＋x －16. (1)求曲线y ＝f (x )在点(2，－6)处的切线的方程；(2)直线l 为曲线y ＝f (x )的切线，且经过原点，求直线l 的方程及切点坐标； 22．（12分）已知函数f (x )＝x 3－3ax －1，a ≠0. (1)求f (x )的单调区间；(2)若f (x )在x ＝－1处取得极值，直线y ＝m 与y ＝f (x )的图像有三个不同的交点，求m 的取值范围．2016届高三上学期第一次月考数学答题卡一、选择题（共12小题，每小题5分，共60分，每小题有一个正确答案）13、 14、15、 16、三、解答题17.(10分) 化简：(1)131421413223b a b a ab b a -(a >0，b >0)；(2)(－278)23-＋(0.002)12-－10(5－2)－1＋(2－3)0.18．(10分)已知函数f (x )＝1a －1x(a >0，x >0)，(1)求证(用单调性的定义证明)：f (x )在(0，＋∞)上是增函数； (2)若f (x )在[12，2]上的值域是[12，2]，求a 的值．19．（12分）已知定义在R 上的奇函数f (x )有最小正周期2，且当x ∈(0,1)时，f (x )＝2x4x ＋1.(1)求f (1)和f (－1)的值； (2)求f (x )在[－1,1]上的解析式．20．（12分）已知函数f(x)＝x3＋x－16.(1)求曲线y＝f(x)在点(2，－6)处的切线的方程；(2)直线l为曲线y＝f(x)的切线，且经过原点，求直线l的方程及切点坐标；21．（13分）已知函数f(x)＝x2＋2ax＋3，x∈[－4,6]．(1)当a＝－2时，求f(x)的最值；(2)求实数a的取值范围，使y＝f(x)在区间[－4,6]上是单调函数；(3)当a＝1时，求f(|x|)的单调区间．22．（13分）已知函数f(x)＝x3－3ax－1，a≠0.(1)求f(x)的单调区间；(2)若f(x)在x＝－1处取得极值，直线y＝m与y＝f(x)的图像有三个不同的交点，求m的取值范围．2016届高三上学期第一次月考数学文试卷参考答案1．B2.A3.D4.D5.D6.A7.A8.D9.B10.B11.B12.A13. x －y －2＝0 14. {x |－32<1}<="" p="">15. (0,1] 16. (512，34]17. 解 (1)原式＝121311113233211212633311233().a b a b abab ab a b+-++----==(2)原式＝(－278)23-＋(1500)12-－105－2＋1＝(－827)23＋50012－10(5＋2)＋1＝49＋105－105－20＋1＝－1679. 18. (1)证明设x 2>x 1>0，则x 2－x 1>0，x 1x 2>0，∵f (x 2)－f (x 1)＝(1a －1x 2)－(1a －1x 1)＝1x 1－1x 2＝x 2－x 1x 1x 2>0，∴f (x 2)>f (x 1)，∴f (x )在(0，＋∞)上是增函数． (2)解∵f (x )在[12，2]上的值域是[12，2]，又f (x )在[12，2]上单调递增，∴f (12)＝12，f (2)＝2.易得a ＝25.19. 解(1)∵f (x )是周期为2的奇函数，∴f (1)＝f (1－2)＝f (－1)＝－f (1)，∴f (1)＝0，f (－1)＝0. (2)由题意知，f (0)＝0. 当x ∈(－1,0)时，－x ∈(0,1)．由f (x )是奇函数，∴f (x )＝－f (－x )＝－2－x4－x ＋1＝－2x4x ＋1，综上，在[－1, 1]上，f (x )＝2x4x ＋1，x ∈(0，1)，－2x 4x＋1，x ∈(－1，0)，0，x ∈{－1，0，1}.20．解 (1)当a ＝－2时，f (x )＝x 2－4x ＋3＝(x －2)2－1，∵x ∈[－4,6]，∴f (x )在[－4,2]上单调递减，在[2,6]上单调递增，∴f (x )的最小值是f (2)＝－1，又f (－4)＝35，f (6)＝15，故f (x )的最大值是35. (2)∵函数f (x )的图像开口向上，对称轴是x ＝－a ，∴要使f (x )在[－4,6]上是单调函数，应有－a ≤－4或－a ≥6，即a ≤－6或a ≥4. (3)当a ＝1时，f (x )＝x 2＋2x ＋3，∴f (|x |)＝x 2＋2|x |＋3，此时定义域为x ∈[－6,6]，且f (x )＝?x 2＋2x ＋3，x ∈(0，6]，x 2－2x ＋3，x ∈[－6，0]，∴f (|x |)的单调递增区间是(0, 6]，单调递减区间是[－6,0]．21.解 (1)可判定点(2，－6)在曲线y ＝f (x )上．∵f ′(x )＝(x 3＋x －16)′＝3x 2＋1.∴f ′(x )在点(2，－6)处的切线的斜率为k ＝f ′(2)＝13. ∴切线的方程为y ＝13(x －2)＋(－6)，即y ＝13x －32.(2)法一设切点为(x 0，y 0)，则直线l 的斜率为f ′(x 0)＝3x 20＋1，∴直线l 的方程为y ＝(3x 20＋1)(x －x 0)＋x 30＋x 0－16，又∵直线l 过点(0,0)，∴0＝(3x 20＋1)(－x 0)＋x 30＋x 0－16，整理得，x 30＝－8，∴x 0＝－2，∴y 0＝(－2)3＋(－2)－16＝－26，k ＝3×(－2)2＋1＝13. ∴直线l 的方程为y ＝13x ，切点坐标为(－2，－26.) 法二设直线l 的方程为y ＝kx ，切点为(x 0，y 0)，则k＝y0－0x0－0＝x30＋x0－16x0又∵k＝f′(x0)＝3x20＋1，∴x30＋x0－16x0＝3x2＋1，解之得x0＝－2，∴y0＝(－2) 3＋(－2)－16＝－26，k＝3×(－2)2＋1＝13.∴直线l的方程为y＝13x，切点坐标为(－2，－26)．22.解(1)f′(x)＝3x2－3a＝3(x2－a)，当a<0时，对x∈R，有f′(x)>0，∴当a<0时，f(x)的单调增区间为(－∞，＋∞)．当a>0时，由f′(x)>0，解得x<－a或x>a.由f′(x)<0，解得－a<x<a，< p="">∴当a>0时，f(x)的单调增区间为(－∞，－a)，(a，＋∞)，单调减区间为(－a，a)．(2)∵f(x)在x＝－1处取得极值，∴f′(－1)＝3×(－1)2－3a＝0，∴a＝1.∴f(x)＝x3－3x－1，f′(x)＝3x2－3，由f′(x)＝0，解得x1＝－1，x2＝1.由(1)中f(x)的单调性可知，f(x)在x＝－1处取得极大值f(－1)＝1，在x＝1处取得极小值f(1)＝－3.∵直线y＝m与函数y＝f(x)的图像有三个不同的交点，结合如图所示f(x)的图像可知：实数m的取值范围是(－3,1)．</x<a，<>。

湖北省钟祥市第一中学2016届高三5月适应性考试（一）语文试题注意事项：1．本试题分第I卷（阅读题）和第Ⅱ卷（表达题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在试题卷和答题卷上，并将准考证号条形码粘贴在答题卡上的指定位置。

用统一提供的2B铅笔把答题卡上试卷类型（A或B）的方框涂黑。

2．选择题的作答：每小题选出答案后，用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

答在试题卷、草稿纸上无效。

3．非选择题的作答：用统一提供的签字笔直接答在答题卡上对应的答题区域内，答在试题卷、草稿纸上无效。

4．考生必须保持答题卡的整洁。

考试结束后，请将本试卷和答题卡一并上交。

第I卷（阅读题，共70分）甲必考题一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1～3题。

2015年是抗战胜利70周年，当全国人民都在纪念抗日英雄的时候，现实生活中却有一种不良的文化现象日益明显，这就是英雄叙事的扭曲问题。

比如，大量抗战“雷剧”“神剧”涌现，将严肃的抗战历史娱乐化；有人对抗战中的英雄人物进行解构乃至重构，试图颠覆或终结相关英雄的经典形象。

随着移动互联网时代的到来，以微博、微信、微视频、客户端为代表的“三微一端”全面渗透进人们的日常生活。

一些错误的英雄叙事借助新媒介，传播范围更广，受众更多，产生了更加恶劣的影响。

比如，近年来互联网上出现了不少诋毁邱少云、狼牙山五壮士的各种扭曲的“英雄叙事”。

媒体把这类叙事的“主体”命名为“凿船党”，并表达了对他们的警惕：“他们每天寻寻觅觅，看见正面的东西就上去凿几下子，而且每每有所斩获，用着放大镜在英雄身上发现了一些瑕疵，他们便极力将其放大。

慢慢地，一些英雄的形象开始坍塌。

”与此同时，一些抗战题材影视剧不顾历史本真，肆意将爱情、悬疑、性感、时尚等元素塞进来，这种做法是对英雄形象的亵渎，以至连普通观众对“手撕鬼子”之类不靠谱的剧情都忍无可忍。

湖北省钟祥市第一中学2016届高三5月适应性考试（一）文科综合能力试题★祝考试顺利★考生注意：1．答题前，考生务必将自己的姓名、班级填写在答题卡上。

2．第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

第Ⅱ卷用黑色签字笔在答题卡上书写作答，在试题卷上作答，答案无效。

3．考试结束，监考员将答题卡按序收回。

第Ⅰ卷（选择题共140分）本卷共35小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

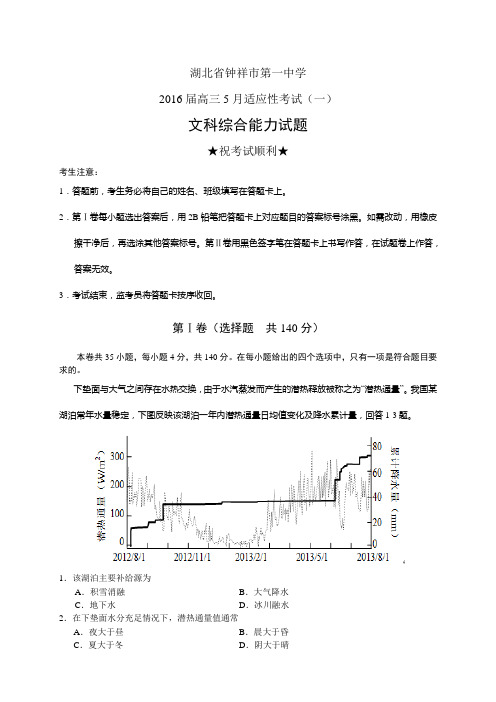
下垫面与大气之间存在水热交换，由于水汽蒸发而产生的潜热释放被称之为“潜热通量”。

我国某湖泊常年水量稳定，下图反映该湖泊一年内潜热通量日均值变化及降水累计量，回答1-3题。

1．该湖泊主要补给源为A．积雪消融B．大气降水C．地下水D．冰川融水2．在下垫面水分充足情况下，潜热通量值通常A．夜大于昼B．晨大于昏C．夏大于冬D．阴大于晴3．对该湖泊12-2月潜热通量值的表现，合理的解释是A．下渗强烈B．湖面结冰C．云量增大D．风速减小下图为我国某区域图，为适应发展需要，该区域正在增修铁路新线。

读图回答4-6题。

4．在建铁路线路选择，最主要为了A．保护铁路沿线植被B．减轻洪水对铁路破坏C．提高区域客运运能D．降低铁路修建工程量5．乙、丙两站间铁路沿线河谷地带自然植被稀疏，主要是因为A．光照不足B．水源短缺C．土壤贫瘠D．下沉气流6．有乘客某日在丙站站前广场发现自己阳光下身影朝北且与身高大致等长，则此日可能是A．5月1日B．6月22日C．10月1日D．12月1日澜沧江—湄公河发源于中国青海省唐古拉山脉，向南流至云南省南腊河口出境，在越南胡志明市以南注入太平洋。

读“该流域人口密度、人口总量与高程分布图”及“澜沧江流域居民点分布比例与坡向关系图”，完成7－9题。

7．图示信息显示A．人口密度随高度变化并不明显B．0～400米人口分布随高程增大迅速增加C．5000米以上可能有大片无人区D．流域人口分布的态势是南疏北密8．与人口密度分布关系最密切的是A．太阳辐射能B．土地利用方式C．水能资源D．年降水量9．由澜沧江流域居民点分布与坡向的关系可知A．与村相比乡镇选址更趋向采光好的方向B．坡向对居民点的影响主要表现在降水时间上C．居民点在坡向的选择上与山体走向无关D．乡镇居民点分布比例最少的是正北方向上世纪90年代以来，我国许多城市人口与就业分布时空变化明显，读下图回答10-11题。

2016届湖北省高中毕业生5月模拟考试数学（文科）试题文科数学第Ⅰ卷一、选择题（本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项 是符合题目要求的.）1.复数21ii -=-（ ） A ．322i - B ．322i + C ．322i -+ D ．322i --2.已知集合U R =，集合{}{}2|20,|1A x x x B x x =--≥=≥，则()R C A B = （ ） A ．{}|11x x -<< B ．{}|12x x ≤≤ C ．{}|11x x -≤< D ．{}|12x x ≤<3.“若222x y +>，则1x >或1y >”的否命题是（ ）A ．若222x y +≤，则1x ≤或1y ≤B ．若222x y +<，则1x <或1y < C ．若222x y +<，则1x <或1y < D ．若222x y +≤，则1x ≤或1y ≤4.已知,y x 满足约束条件5020x y x x y -+≥⎧⎪≤⎨⎪+≥⎩则2z x y =+的最小值为（ ） A ．-3 B ．52-C ．-2D ．525.下图是一个算法的程序框图，该算法所输出的结果是（ ）A ．23 B ．34 C ．45 D ．566.已知双曲线221x my +=的虚轴长是实轴长的两倍，则双曲线的离心率e =（ ） ABD ．27.已知等比数列{}n a 满足11352,14a a a a =++=，则135111a a a ++=（ ） A ．78 B ．74 C ．139 D ．13188.已知M 为ABC ∆内一点，1134AM AB AC =+，则ABM ∆和ABC ∆面积之比为（ ）A ．14B ．13C ．12D ．239.已知函数()222cos f x x x =-，下面结论中错误的是（ ）A ．函数()f x 的最小正周期为πB ．函数()f x 的图象关于3x π=对称C ．函数()f x 的图象可由()2sin 21g x x =-的图象向右平移6π个单位得到D ．函数()f x 在区间0,4π⎡⎤⎢⎥⎣⎦上是增函数 10.一个四面体的三视图如下，则此四面体的体积是（ ）AC．． 11.已知,y x 满足2213x y +=，则2432u x y x y =+-+--的取值范围为（ ）A ．[]1,12B ．[]0,6C ．[]1,12D ．[]1,1312.过双曲线22:145x y C -= 的右焦点F 的直线l 与双曲线C 交于M N 、两点，A 为双曲线的左顶点，若直线AM 与直线AN 的斜率12,k k 满足122k k +=，则直线l 的方程为（ ） A ．()23y x =- B ．()22y x =-- C ．()132y x =- D ．()132y x =-- 第Ⅱ卷二、填空题：（本大题共4小题，每小题5分，满分20分，将答案填在答题纸上）13.已知等差数列{}n a 的前n 项和2n S n =，则数列{}n a 的公差d =____________．14.已知两点()3,2A 和()1,4B -到直线10x ay ++=的距离相等，则实数a =_____________．15.已知三棱锥P ABC -中，4,6,PA AB AC BC PA ====⊥平面ABC ，则此三棱锥的外接球的半径为_____________．16.已知函数()()312,12,x x x tf x a x x t⎧->⎪=⎨-+≤⎪⎩，如果对一切实数t ，函数()f x 在R 上不单调，则实数a 的取值范围是_________________．三、解答题 （解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分12分）在ABC ∆中，角A B C 、、的对边分别为3,,,,cos 4a b c A B AD π==为BC 边上的中线，且1AD =．（1）求sin C 的值；（2）求AC 边的长． 18.（本小题满分12分）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是菱形，4,2PA AC BD ===，又E 在PC 上，且PC ⊥平面BDE ．（1）求CE 的长；（2）求点A 到平面PDC 的距离． 19.（本小题满分12分）某年级中两个班级的同学准备报名参加义务劳动，甲班有1名男同学和2名女同学报名，乙班有1名男同学和1名女同学报名．（1）若从两个班报名的同学中各选1名同学，求2名同学是异性同学的概率；（2）若从报名的5名同学中任选2名同学，求这2名同学不能同时来自同一个班的概率． 20.（本小题满分12分）（1）已知()2ln f x x ax =-，求()f x 的单调区间；（2）若()0f x ≤，对0x >恒成立，求a 的取值范围． 21.（本小题满分12分）已知抛物线()2:20C y px p =>的焦点为F ，过F 且倾斜角为4π的直线l 被抛物线C 截得的线段长为8．（1）求抛物线C 的方程；（2）已知直线y x =-和抛物线C 交于点O A 、．线段AO 的中点为Q ，在AO 的延长线上任取一点P 作抛物线C 的切线，两人切点分别为M N 、，直线MQ 交抛物线C 于另一点B ．问直线NB 的斜率0k 是否为定值？如果是，求0k 的值，否则，说明理由．请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）选修4-1：几何证明选讲如图，ABC ∆为O 的内接三角形，D E 、分别为BC AB 、的中点，直线DE 交圆O 于F G 、，且直线DE与过A 点的切线交于点P ，1,2,3DF DE PE ===．（1）求证：PEA BDE ∆∆ ； （2）求线段PA 的长．23. （本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线[)3:,0,22cos C ρθπθ=∈-，直线l 的方程为322x t y t =+⎧⎨=+⎩（t 为参数，t R ∈）． （1）求曲线C 和直线l 的普通方程；（2）设直线l 和曲线C 交于A B 、两点，求AB 的值． 24. （本小题满分10分）选修4-5：不等式选讲已知函数()()422f x x a x a R =-+++∈的图象关于点()1,0中心对称． （1）求实数a 的值； （2）解不等式()3f x ≥．参考答案一、选择题二、填空题 13. 2 14. 2或23- 15. 4 16. 1a ≤ 三、解答题17.解：（1）在ABC ∆中，cosB =sin B ==∴()sin sin sinAcosB cosAsinB C A B =+=+cosB B ===，∴sin C =6分（2）由（1）知sin :sin :sin ::A B C a b c ===令,,a b x c ===，解得2x =，∴AC 边的长为2．．．．．．．．．．．．．．．．．．．．．．．．．．．12分 18.解：（1）在P ABCD -中，PC ⊥面,DEB BD AC O = ，连接OE ，则OE PC ⊥．在Rt PAC ∆中，4,PA AC ==∴PC ==∴A 到PC 的距离1d ==，则OE =． 在Rt OEC ∆中，22233734934777CE OC OE ⨯-⨯=-=-== ．∴CE ==．．．．．．．．．．．．．．．．．．．．．．．．．4分（2）又2PC DC ==，∴PDC ∆面积S ===在四面体A PDC -中，设A 到面PDC 的距离为d ．∴1133PDC ADC d S S PA ∆∆=，∴d =∴点A 到平面PDC．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分19.解：（1）甲选男且乙选女的概率1111326P == ， 甲选女且乙选男的概率2211323P == ， ∴111632P =+=．．．．．．．．．．．．．．．．．．．．．．．4分 （2）从5名同学中任选2名共有10种方法，2名同学全来自甲班的选法有3种，2名同学全来自乙班的选法有1种，∴同时来自于同一个班的概率312105P +==． ∴不能来自于同一个班的概率23155P =-=．．．．．．．．．．．．．．．．．．．．．．．12分20.解：（1）()21122,0ax f x ax x x x-'=-=>．①若0a ≤，则()0f x '>，()f x 在()0,+∞单调递增； ②若0a >，由()0f x '=，得x =，当0x <<时，()0f x '>，()f x在⎛⎝上单调递增，当x >()0f x '<，()f x在⎫+∞⎪⎭上单调递减．．．．．．．．．．．．．．．．．．．．．．．．4分 （2）由()0f x ≤，得22ln ln 0,xx ax a x -≤≥， 记()2ln x g x x=，则()24312ln 12ln ,0x x xx x g x x x x --'==> ，当x >()()0,g x g x '<在)+∞单调递减；当0x <<时，()()0,g x g x '>在(上单调递增；∴()max 12g x ge ==，∴12a e≥．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分 21.解：（1）过F 且倾角为4π的直线:y x 2pl =-交抛物线22y px =于K 和L ，由22p y py y ⎛⎫=+⎪⎝⎭，得2220y py p --=， ∴22,K L k L y y p y y p +==- ，48p -==．∴抛物线方程为24y x =．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分 （2）联立24y xy x=-⎧⎨=⎩解得()()0,0,4,4O A -，OA 的中点()2,2Q -． 设点(),P m m -，切点()()1122,,,M x y N x y ．过M 的切线：()112y y x x =+，因为切线过(),m m -，则()()1122y m x +-=， 同理可知()()2222y m x +-=，两式相除，得到2111222222y x y y x y +==+，化简得：()()()122112122y y y y y y y y -=-+，而12y y ≠， ∴()12122y y y y =--，即12122y y y -=+． MQ 方程：()()1121122222224y y y x x y x +++=-=---，联立24y x =，得()222111122222220444y y y y y y ⎛⎫⎛⎫+---+---= ⎪ ⎪⎝⎭⎝⎭， ∴211182B y y y y -+=+，则()21111124822B y y y y y y -+-=-=++．∴()1211144124222NB B k y y y y y y ===--++-+++．∴直线NB 的斜率为定值．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分22.解：（1）∵PA 是过A 点的切线， ∴BAP BCA ∠=∠.而//DE AC ，即BCA BDE ∠=∠，又BEA PEA ∠=∠，∴PAE BDE ∆∆ ．．．．．．．．．．．．．．．．．．．．5分 （2）设,PG y GE x ==，则3x y +=，PA BD BE ===，∵PAE BDE ∆∆ ，∴EB PE BD AP == ∴1223x x y x y ⎧=⎪+⎨⎪+=⎩，解得21x y =⎧⎨=⎩或1252x y ⎧=⎪⎪⎨⎪=⎪⎩，∴PA ==PA ==．．．．．．．．．．．．．．．．．．．．．．．．10分23.解：（1）由32cos ρθ=-，得2cos 3ρρθ-=，∴()()2223cos ρρθ=+，即()()22243x yx +=+，∴()221143x y -+=． ∵322x t y t =+⎧⎨=+⎩（t 为参数），∴223y x -=-， ∴24y x =-．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．5分（2）24y x =-代入()221143x y -+=，设()()1122,,,A x y B x y ， 21970550x x -+=，12127055,1919x x x x +==，()221212124x x x x x x -=+-2222704551919704551919⨯=--⨯⨯=6019=．．．．．．．．．．．．．．．．．．．．．．．．．．．10分 24.解：（1）∵()y f x =关于点()1,0中心对称， 则有()()420f f +-=，∴660,1a a +==-， 在1a =-时，()42f x x x =--+， 而()()()22422f x x x -=----+ ()24x x f x =+--=-∴()()20f x f x +-=，故()y f x =关于()1,0对称，∴1a =-．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．5分（2）()423f x x x =--+≥，①在4x ≥时，()()423x x --+≥，不可能， ②在2x ≤-时，()()423x x -++≥，恒成立．③在24x -<<时，()42322321x x x x --+≥⎧⎪-≥⎨⎪≤-⎩，∴122x -<≤-． 综合①②③可知：12x ≤-．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分。

2016年适应性考试文科数学一、选择题:本大题共12小题,每小题5分,共60分．在每小题给出的四个选项中,只有一项是符合题目要求的．1．已知集合2{560}A x x x =-+≤，{21}x B x =>，则A B =（ ）A ．[2,3]B ．(0,)+∞C ．(0,2)(3,)+∞D ．(0,2][3,)+∞【答案】A【解析】∵[2,3]A =，(0,)B =+∞，∴[2,3]A B =．2．设复数132i z =+，21i z =-，则122z z +=（ ）A ．2B ．3C ．4D ．5 【答案】D【解析】122232i 1iz z +=++-32i (1i)43i 5=+++=+=．3．甲，乙，丙三名学生随机站成一排，则甲站在边上的概率为（ ）A ．13B ．23C ．12D ．56【答案】B【解析】甲任意站位有3种，甲站在边上的情况有2种，∴23P =．4．设,p q 是两个题，若p q ⌝∧是真命题，那么（ ）A ．p 是真命题且q 是假命题B ．p 是真命题且q 是真命题C ．p 是假命题且q 是真命题D ．p 是真命题且q 是假命题【答案】C5．已知等比数列{}n a 满足：1310a a +=，4654a a +=，则{}n a 的通项公式n a =（） A ．412n - B ．312n -C ．3142n -+D ．2162n -+【答案】A【解析】∵3461318a a q a a +==+，∴12q =．由1310a a +=，得18a =，∴1114118()22n n n n a a q ---==⨯=．。

高中数学学习材料马鸣风萧萧*整理制作试卷类型：B钟祥一中高三五月适应性考试（一）数学（理科）试题命题人： 审题人：范德宪考试时间： 15：00—17：00★祝考试顺利★注意事项：1．本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答第I 卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再涂其他答案标号．写在本试卷上无效．3．回答第II 卷时, 用0．5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内，将答案写在答题卡上，写在本试卷上无效．第I 卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．定义集合{}|A B x x A x B -=∈∉且，若集合{},2,3,4,5,M =1集合{}21,N x x k k Z ==-∈，则集合MN -的子集个数为( )A ．2B ．3C ．无数个D ． 4 2．i 为虚数单位，复数2016i 的共轭复数为( )A ．iB ．1C ．－1D ．－i3．某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩(满分100分)的茎叶图如图，其中甲班学生成绩的中位数是83，乙班学生成绩的平均数是86，则x ＋y 的值为( )A ．168B ．9C ．8D ．1694．命题:,sin()cos p R απαα∃∈-=；命题:"04"q a <<是”关于x的不等式210ax ax ++>的解集是实数集"R 的充分必要条件，则下面结论正确的是（ ）A ． ""p q ∧是假命题B ． q 是真命题C ．p 是假命题D ． ""p q ∨是假命题5．执行右边的程序框图，当2,n n N *≥∈ 时，()n f x 表示1()n f x -的导函数，若输入函数1()sin cos f x x x =-，则输出的函数()n f x 可化为（ ）A ．2sin 4x π⎛⎫+ ⎪⎝⎭B ．2sin 4x π⎛⎫- ⎪⎝⎭C ． 2sin 4x π⎛⎫-+⎪⎝⎭D ． 2sin 4x π⎛⎫--⎪⎝⎭6．在明朝程大位《算法统宗》中有这样的一首歌谣：“ 远看巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯”。

湖北省2016届高三数学5月模拟试卷（文含答案）湖北省2016届高中毕业班五月模拟考试文科数学第Ⅰ卷一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1、复数A．B．C．D．2、已知全集，集合，则A．B．C．D．3、“若”，则“”的否命题是A．若则且B．若则且C．若则或D．若则或4、已知满足约束条件，则的最小值为A．-3B．C．-2D．5、右图是一个算法的程序框图，该算法所输出的结果是A．B．C．D．6、已知双曲线的虚轴长是实轴长的两倍，则双曲线的离心率A．B．C．D．27、已知等比数列满足，则A．B．C．D．8、已知M为内一点，，则和的面积之比为A．B．C．D．9、已知函数，下面结论中错误的是A．函数的最小正周期为B．函数的图象关于对称C．函数的图象可由的图象向右平移个单位得到D．函数在区间上是增函数10、一个四面体的三视图如下，则此四面体的体积是A．B．C．D．11、已知满足，则的取值范围为A．B．C．D．12、过双曲线的右焦点F的直线与双曲线C交于C交于两点，A为双曲线的左焦点，若直线AM与直线AN的斜率满足，则直线的方程是A．B．C．D．第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上。

.13、已知等差数列的前n项和，则数列的公差14、已知两点和到直线的距离相等，则实数15、已知三棱锥中，平面，则此三棱锥的外接球的半径为16、已知函数，如果对一切实数，函数在上不单调，则实数的取值范围是三、解答题：本大题共6小题，满分70分，解答应写出文字说明、证明过程或演算步骤17、（本小题满分12分）在中，角的对边分别为为边上的中线，且.（1）求的值；（2）求的面积。

18、（本小题满分12分）如图，在四棱锥中，平面，底面是菱形，，，又点在侧棱上，且平面.（1）求线段的长；（2）求点A到平面的距离。

19、（本小题满分12分）某年级中两个班级的同学准备报名参加义务劳动，甲班有1名男同学和2名女同学报名，乙班有1名男同学和1名女同学报名。

高中化学学习材料鼎尚图文收集整理湖北省钟祥市第一中学2016届高三5月适应性考试（一）理科综合试题化学试题命题人：赵威关平黄大军审题人：邓家茂向荣锋黄诚考试时间：2016年5月11日上午9：00—11：30★祝考试顺利★可能用到的相对原子质量：H：1 C：12 N：14 O：16 Na：23 Cl：35.5 Cu：64 Zn：657. 化学与生产、生活密切相关，背景材料：①北大研制的石墨烯弹性气凝胶（又名碳海棉）入选2013年度世界最轻固体材料；② 2014年11月上旬北京APEC峰会期间，政府重拳整治雾霾，蓝天重现；③用铂丝或无锈铁丝可用来进行钠、钾、铜、钡、锶等的焰色反应④瑞典皇家理工学院（KTH）的研究人员已经成功地构建出了一种能使水快速分解的分子催化剂。

下列说法不正确的是A．石墨烯弹性气凝胶可用作处理海上原油泄漏的吸油材料B．压减燃煤、严格控车、调整产业是治理雾霾有效措施C．绚丽缤纷彩色的烟花中添加了含钾、钠、铁、铜等金属化合物D．使用该分子催化剂可将一次能源太阳能直接转化成二次能源，例如电能、氢能8．能正确表示下列反应的离子方程式是A．向次氯酸钠溶液中通入足量SO2气体：ClO-＋SO2＋H2O==HClO＋HSO3-B．0.1mol/LNH4Al(SO4)2溶液与0.2mol/LBa(OH)2溶液等体积混合：Al3+＋2SO42-＋2Ba2+＋4OH- ＝2BaSO4↓＋AlO2-＋2H2OC．用浓盐酸酸化的KMnO4溶液与H2O2反应，证明H2O2具有还原性：+ 6H+ + 5H2O2＝2Mn2+ + 5O2↑ + 8H2O2MnO4D．Fe2O3溶于过量氢碘酸溶液中：Fe2O3＋6H+ ＋2I-=2Fe2+＋I2 ＋3H2O9．设N A为阿伏加德罗常数，下列叙述正确的是①lmolCH3CH2C(CH3)3所含甲基个数为4N A②2.8g乙烯和2.8g聚乙烯中含碳原子数均为0.2N A③1.0L1.0mol/LCH3COOH溶液中，CH3COOH分子数为N A④8.8g乙酸乙酯中含共用电子对数为1.4N A⑤标准状况下，22.4L乙醇完全燃烧后生成CO2的分子数为2N A ⑥常温常压下，17g甲基（—14CH3）所含的中子数为9N A ⑦标准状况下，11.2L氯仿中含有C—Cl键的数目为1.5N A ⑧lmolC15H32分子中含碳碳键数目为14N AA．①③⑤⑦B．①②④⑧C．②③⑥⑧D．①②⑥⑧10．室温下向10 mL 0.1 mol·L－1NaOH溶液中加入0.1 mol·L－1的一元酸HA，溶液pH的变化曲线如图所示。

钟祥一中高三五月适应性考试（一）理科数学本试卷共6页，23题。

全卷满分150分。

考试用时120分钟。

★祝考试顺利★本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第22～23题为选考题，其它题为必考题。

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。

2．选择题答案使用2B 铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。

3．考生必须按照题号在答题卡各题号相对应的答题区域内(黑色线框)作答,写在草稿纸上、超出答题区域或非题号对应的答题区域的答案一律无效。

4．保持卡面清洁，不折叠，不破损。

5．做选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。

第I 卷一、选择题：本题共12小题，每小题5分，在每小题给出的四个答案中，只有一项是符合题目要求的。

1．设集合{}12,2,|2M N x x ⎧⎫=-=<⎨⎬⎩⎭，则下列结论正确的是（ ） A. N M ⊆B. M N ⊆C. {}2N M =D. N M R =2．若复数z 满足()121i z i +=-，则复数z 的虚部为（ ） A.35B. 35-C. 35iD.35i -3．已知命题():,0,23x x p x ∀∈-∞>；命题:0,,sin 2q x x x π⎛⎫∃∈> ⎪⎝⎭，则下列命题为真命题的是（ ）A.p q ∧B. ()p q ⌝∨C. ()p q ⌝∧D. ()p q ∧⌝4．已知向量,a b满足()1,2,3,2a b a b ==-=，则2a b +=（ ）A. 22B. 17C.15D.255．已知函数f (x )＝⎩⎪⎨⎪⎧x 2，0≤x <1，1x，1≤x ≤e (e 为自然对数的底数)的图象与直线x ＝e 、x 轴围成的区域为E ，直线x ＝e 、y ＝1与x 轴、y 轴围成的区域为F ，在区域F 内任取一点，则该点落在区域E 内的概率为（ ）A. 2eB. 23eC. 23D. 43e6．一个侧棱与底面垂直的棱柱被一个平面截去一部分所剩几何体的三视图如图所示，则该几何体的体积为（ ） A ．9 B ．10C ．11D ．2327．“绿水青山就是金山银山”，为优化山林，某林场计划更新树种，增栽 桂花树、香樟树各x 、y （单位：百棵），整数,x y 满足2527x y x y x ->⎧⎪-<⎨⎪<⎩，则栽种这两种树的总数最多为( )百棵（ ） A. 12B. 13C.14D.158．已知数列{}n a 为等比数列，则,6,5117144=⋅=+a a a a =1020a a （ ）A ．2332或B ．23-32-或 C ．32D ．23 9．已知双曲线C:191622=-y x 与直线L:05=--k y kx 交于A ，B 两点，若8=AB ，则直线L 有（ ）条 （ ） A ．1B ．2C ．3D ．410．习总书记在十九大报告中指出：坚定文化自信，推动社会主义文化繁荣兴盛．如图，“大衍数列”：0,2,4,8,12来源于《乾坤谱》中对《易传》“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和．下图是求大衍数列前项和的程序框图．执行该程序框图，输入，则输出的（ ）A ．44B ．68C ．100D ．14011．将函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移12π个单位，再向上平移1个单位，得到函数()g x 的图象，若()()129g x g x =，且[]12,2,2x x ππ∈-，则122x x -的最大值为（ ）A.4912πB.356π C. 256π D.174π12．已知：()2ln 3ln 12ln 3ln ln -+-=a ，()3ln 13ln ln +=b ，()2ln 212ln 2ln ln ++=c ，则c b a ,,的大小关系为（ ）A.a b c <<B. a c b <<C. c a b <<D.c b a <<二、填空题：本大题共4小题，每小题5分，共20分. 13．()20cos a x dx π=-⎰，则912ax ax⎛⎫+ ⎪⎝⎭展开式中，3x 项的系数为 14．已知椭圆22221(0)x y a b a b +=>>的顶点分别为A 、B 、C 、D ，且左右的焦点为12,F F ，且以12F F 为直径的圆内切于四边形ABCD ，则椭圆的离心率为e 为15．在数列{}n a 及{}n b 中，221n n n n n a a b a b +=+++，221n n n n n b a b a b +=+-+，11a =，11b =．设nn n b a c 11+=，则数列{}n c 的前2018项和为 16．两个半径都是()1>r r 的球O 1和球O 2相切，且均与直二面角α﹣l ﹣β的两个半平面都相切，另有一个半径为1的小球O 与这二面角的两个半平面也都相切，同时与球O 1和球O 2都外切，则r 的值为 ． 三、解答题：解答应写出文字说明、证明过程或演算步骤。

试卷类型：A 钟祥一中2016届高三五月适应性考试（一）语文试题命题人：周琴审题人：苏辉李统元考试时间：2016年5月10日9：00—11：30本试卷共10页，六大题，23小题。

全卷满分150分，考试用时150分钟。

★祝考试顺利★注意事项：1．本试题分第I卷（阅读题）和第Ⅱ卷（表达题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在试题卷和答题卷上，并将准考证号条形码粘贴在答题卡上的指定位置。

用统一提供的2B铅笔把答题卡上试卷类型（A或B）的方框涂黑。

2．选择题的作答：每小题选出答案后，用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

答在试题卷、草稿纸上无效。

3．非选择题的作答：用统一提供的签字笔直接答在答题卡上对应的答题区域内，答在试题卷、草稿纸上无效。

4．考生必须保持答题卡的整洁。

考试结束后，请将本试卷和答题卡一并上交。

第I卷（阅读题，共70分）甲必考题一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1～3题。

2015年是抗战胜利70周年，当全国人民都在纪念抗日英雄的时候，现实生活中却有一种不良的文化现象日益明显，这就是英雄叙事的扭曲问题。

比如，大量抗战“雷剧”“神剧”涌现，将严肃的抗战历史娱乐化；有人对抗战中的英雄人物进行解构乃至重构，试图颠覆或终结相关英雄的经典形象。

随着移动互联网时代的到来，以微博、微信、微视频、客户端为代表的“三微一端”全面渗透进人们的日常生活。

一些错误的英雄叙事借助新媒介，传播范围更广，受众更多，产生了更加恶劣的影响。

比如，近年来互联网上出现了不少诋毁邱少云、狼牙山五壮士的各种扭曲的“英雄叙事”。

媒体把这类叙事的“主体”命名为“凿船党”，并表达了对他们的警惕：“他们每天寻寻觅觅，看见正面的东西就上去凿几下子，而且每每有所斩获，用着放大镜在英雄身上发现了一些瑕疵，他们便极力将其放大。

慢慢地，一些英雄的形象开始坍塌。