第三节刚度矩阵
- 格式:doc
- 大小:507.00 KB
- 文档页数:14

rur r u r =-+=πππεθ22)(2由于各点在圆周方向上无位移,因而剪应变θr v 和r v θ均为零。
将应变写成向量的形式,则{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∂∂+∂∂∂∂∂∂=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=r w z u z w r u r u rz z r γεεεεθ根据上式,可推导出几何方程{}[]{})(e B ϕε=其中几何矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∆=ij jikiikjkkj ji ik kj k j i ijkjjkz r z r z rr r r r z r N r z r N r z r N z z z B 0000),(0),(0),(00021 3.弹性方程和弹性矩阵[D]依照广义虎克定律,同样可以写出在轴对称中应力和应变之间的弹性方程,其形式为[])(1θσσσε+-=z r r u E [])(1z r u E σσσεθθ+-=[])(1θσσσε+-=r z z u Erz rz Er τμ)1(2+=所以弹性方程为{}[]{}εσD = 式中应力矩阵{}{}T rz z r τσσσσθ=弹性矩阵[]⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-----+=221000010101)21)(1(μμμμμμμμμμμμED 4.单元刚度矩阵[])(e k与平面问题相同,仍用虚功原理来建立单元刚度矩阵,其积分式为[][][][]dV B D B k VT e ⎰=)(在柱面坐标系中,drdz dV π2=将drdz dV π2=代入[][][][]dV B D B k VT e ⎰=)(,则[][][][]rdrdz B D B k T e ⎰⎰=π2)(即为轴对称问题求单元刚度矩阵的积分式。
与弹性力学平面问题的三角形单元不同,在轴对称问题中,几何矩阵[B]有的元素(如rz r N i ),(等)是坐标r 、z 的函数,不是常量。

各单元的单元刚度矩阵一)杆件单元刚度矩阵局部坐标系中:整体坐标系中:αμαλsin ;cos ==二、)梁单元刚度矩阵剪弯梁局部坐标系下:坐标转换矩阵为:⎥⎦⎤⎢⎣⎡--=1111][l EA ke ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------=l EI l EI l EI l EI l EI l EI l EI l EI l EI l EI l EI l EI l EI l EI l EI l EI k z z z z z z z z z z z z z z z z e 46612266122661246612][223223223223[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=ααααααααcos sin 00sin cos 0000cos sin 00sin cos T轴剪弯梁局部坐标系下:坐标转化矩阵为:三、)平面三节点三角形单元刚度矩阵{}[]{}e N δδ=⎥⎥⎦⎤⎢⎢⎣⎡=m j i m j i N N N N N N N 000000][ )(21y c x b a AN i i i i ++=; ),,(m j i i = j m m j i y x y x a -=,m j i y y b -=,j m i x x c -=。
单元为等腰直角三角形,直角边长为1。
泊松比为0,弹性模量为1。
(单元节点编号为逆时针i ,j ,m ;直角顶点为m )[]⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------=l EI l EI l EI l EI l EI l EI l EI l EI l EA l EA l EI l EI l EI l EI l EI l EI l EI l EI l EA l EA K e 460260612061200000260460612061200000222322222223[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--=1000000sin cos 0000sin cos 0000001000000cos sin 0000sin cos ααααααααT⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------=23211212102302121110002*********][E k e 1)集中力:}{][}{P N R T e =⎭⎬⎫⎩⎨⎧⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧y x y x m m j j i i m m j j i i P P N N N N N N Y X Y X Y X p p ),(000000 2)体力:⎰⎰=tdxdy p N R T e }{][}{3)分布面力:⎰=s T e tds P N R }{][}{例题3:在均质、等厚的三角形单元ijm 的ij 边上作用有沿x 方向按三角形分布的载荷,求移置后的结点载荷。
![[工学]第4章 平面问题的有限元法-3刚度矩阵](https://img.taocdn.com/s1/m/25867d5d31b765ce050814be.png)


matlab计算三节点杆的刚度矩阵
三节点杆的刚度矩阵可以通过以下步骤计算:
1. 定义杆的长度和弹性模量:
L = 杆的长度
E = 弹性模量
2. 定义每个节点的自由度:
例如,节点1有x1和y1两个自由度,节点2有x2和y2两个自由度,节点3有x3和y3两个自由度。
3. 创建刚度矩阵的零矩阵:
K = zeros(6, 6);
4. 计算局部刚度矩阵:
对于每个杆段,计算其局部刚度矩阵:
kl = (E * A / L) * [1 0 0 -1 0 0;
0 0 0 0 0 0;
0 0 0 0 0 0;
-1 0 0 1 0 0;
0 0 0 0 0 0;
0 0 0 0 0 0];
这里,A是杆截面的面积。
5. 计算全局刚度矩阵:
对于每个杆段,将局部刚度矩阵贡献到全局刚度矩阵中: K([2*i-1 2*i 2*i+1],[2*i-1 2*i 2*i+1]) = K([2*i-1 2*i
2*i+1],[2*i-1 2*i 2*i+1]) + kl;
这里,i表示第i个杆段。
完成以上步骤后,K就是所求的三节点杆的刚度矩阵。
注意:根据具体情况,可能需要对杆进行编号或者使用其他方式来确定节点的自由度和局部刚度矩阵的位置。
此外,刚度矩阵的尺寸也可以根据实际情况进行调整。
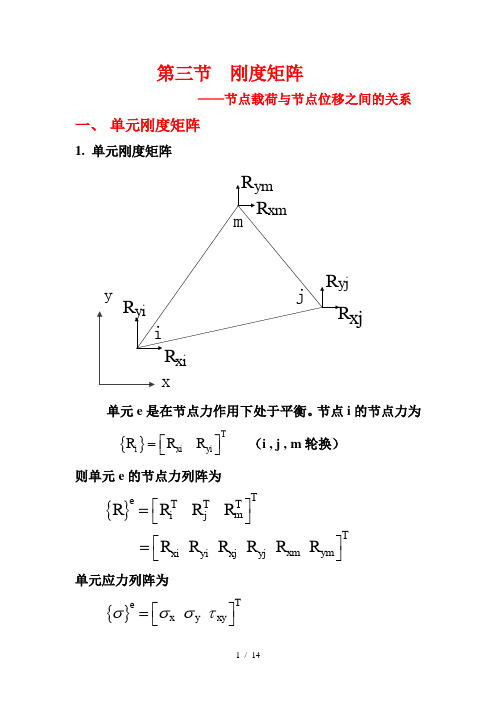
第三节 刚度矩阵——节点载荷与节点位移之间的关系一、 单元刚度矩阵1. 单元刚度矩阵xj单元e 是在节点力作用下处于平衡。
节点i 的节点力为{}Ti xiyi R R R ⎡⎤=⎣⎦ (i , j , m 轮换)则单元e 的节点力列阵为{}TeTT T mi jTxm ym xi yi xj yj R R R R R R R R R R ⎡⎤⎣⎦⎡⎤⎣⎦==单元应力列阵为{}Tex y xy σσστ⎡⎤⎣⎦=假定弹性体的所有节点都产生一虚位移,单元e 的三个节点的虚位移为{}*******eT mm i i j ju v u v u v δ⎡⎤⎣⎦= 单元虚应变列阵为{}****Tx y xy εεεγ⎡⎤⎢⎥⎣⎦=参照式(3-7),则单元虚应变为{}{}**eeB εδ⎡⎤⎣⎦=作用在弹性体上的外力在虚位移上所做的功为:{}{}*eTe R δ⎛⎫ ⎪⎝⎭单元内的应力在虚应变上所做的功为:{}{}*Te tdxdy εσ∆⎛⎫ ⎪⎝⎭⎰⎰根据虚位移原理,可得单元的虚功方程{}{}{}{}**eTTe e R tdxdy δεσ∆⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=⎰⎰或{}{}{}{}**eTTTe e B R tdxdy δδσ∆⎛⎫⎛⎫⎡⎤ ⎪⎪⎣⎦⎝⎭⎝⎭=⎰⎰故有{}{}eTB R tdxdy σ∆⎡⎤⎣⎦=⎰⎰将式(3-10)代入,的{}{}{}eeeTTD B D B R B B tdxdytdxdy δδ∆∆⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦==⎰⎰⎰⎰(3-27)简记为{}{}ee ek R δ⎡⎤⎣⎦= (3-29)--------上式表征单元节点力与节点位移之间的关系,称为单元刚度方程(单元平衡方程) 其中TeD B B k tdxdy ∆⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦=⎰⎰(3-28) ek ⎡⎤⎣⎦称之为单元刚度矩阵(简称为单刚),是66⨯矩阵。
如果单元的材料是均质的,矩阵D ⎡⎤⎣⎦中的元素也是常量,且在三角形常应变的情况下,矩阵B ⎡⎤⎣⎦中的元素也是常数,当单元的厚度也是常数时,注意到dxdy ∆=∆⎰⎰,于是单元刚度矩阵可简化为TeB D B t k ⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦∆= (3-30)将单元刚度矩阵按节点号写成分块矩阵形式:66eii ij imji jj jm mm mimj kk k k k k k k k k ⨯⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦= (3-31)其中任一子块[]rs k (r ,s=i ,j ,m )是一个2×2子矩阵,为[][][][]Trsrs k B D B t =∆ (r ,s=i ,j ,m )(1)对于平面应力问题将[]B 和平面应力问题的弹性矩阵[]D 代入,得Trs r s k B D B t ⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦=∆ ()21122114122r s r s r s r s r s r s r s r s b b c c b c c b Et c b b cc c b b μμμμμμμ--⎡⎤++⎢⎥=⎢⎥---∆⎢⎥++⎢⎥⎣⎦(r ,s=i ,j ,m ) (3-32)(2)对于平面应变问题将[]B 和平面应变问题的弹性矩阵[]D 代入,得()()()()()()()1212211211121212121e rs k b b c c b c c b r s r s r s r s E t c b b c c c b b r s r s r s r sμμμμμμμμμμμμμμμ⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦--++----=--++--- (r,s=i ,j ,m ) (3-33)(注:是将式(3-32)中的,E μ分别换成21E μ- 和1μμ-)2. 单元刚度矩阵的性质 (1)ek ⎡⎤⎣⎦的物理意义式(3-29)可完整写为131415161112212223242526333435363132434445464142555152535456616263646i i jjmmeU k k k k k k V k k k k k k k k k k U k k k k k k k k V k k k k k k U k k k k k V⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=⎧⎫⎪⎪⎪⎪⎪⎪⎨⎬⎪⎪⎪⎪⎪⎪⎩⎭566ii j j m m eu v u v u k v ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎢⎥⎥⎣⎣⎦⎦⎧⎫⎪⎪⎪⎪⎪⎪⎨⎬⎪⎪⎪⎪⎪⎪⎩⎭可见每个节点在x 和y 方向上有二个平衡方程,3个节点共有六个平衡方程。
刚度矩阵存在负值-回复刚度矩阵存在负值是一个非常重要且复杂的问题,它涉及到结构力学的基本原理以及数学建模的技术。
本文将一步一步回答关于刚度矩阵存在负值的问题,并进行详细的解释和分析。
第一步:了解刚度矩阵在开始深入讨论之前,我们先简要了解一下什么是刚度矩阵。
刚度矩阵是一个将结构系统的各个节点之间的位移和力的关系表示为线性方程组的矩阵。
它描述了结构系统的刚度(即抵抗形变的能力)和连接节点之间的刚性关系。
第二步:定位问题当我们得知刚度矩阵存在负值时,首先需要定位到具体的结构体系,例如梁、桁架、柱等等。
不同的结构体系存在不同的刚度矩阵表示方法和计算方式。
因此,我们需要将问题具体化,以便更好地分析和解决。
第三步:检查模型质量一种导致刚度矩阵存在负值的原因是模型质量不好。
这可能涉及到建模过程中的误差或近似、边界条件的设定问题以及模型的不完全性。
在这一步,我们应该检查模型是否准确地反映了实际情况,是否符合结构体系的特性和行为。
第四步:检查力学条件是否满足在解析方法中,刚度矩阵是通过结构体系的位移和力的平衡方程推导得到的。
因此,一种导致刚度矩阵存在负值的可能原因是力学条件不满足。
我们需要检查刚度矩阵的推导是否依据正确的平衡方程,力的边界条件是否正确应用,以及其他与力的计算相关的因素。
第五步:分析材料性质材料的性质直接影响刚度矩阵的计算结果。
一种导致刚度矩阵存在负值的原因是材料的非线性特性未考虑或错误地考虑。
例如,在弹性力学中,应力和应变之间的关系是线性的;然而,在非线性材料中,这种关系可能是非线性的。
因此,我们需要检查材料的特性和模型是否一致,并采取适当的计算模型来获得正确的刚度矩阵。
第六步:重新计算刚度矩阵在排除其他可能性后,如果刚度矩阵仍然存在负值,则需要重新计算刚度矩阵。
这可能涉及到使用更精确的数值计算方法、改进模型的准确性以及检查和校正输入数据的准确性。
总结:刚度矩阵存在负值是一个复杂而关键的问题。
在解决这个问题的过程中,我们需要依次检查模型质量、力学条件的满足性和材料的性质,并采取相应的纠正措施。
悬置中系统的刚度矩阵-回复系统的刚度矩阵是结构动力学中的一个重要概念。
它用于描述系统辨识度的能力,并且在许多工程问题的分析和求解中起着关键作用。
在本文中,我将一步一步地回答以下问题:什么是系统的刚度矩阵?如何推导系统的刚度矩阵?系统的刚度矩阵有什么应用?一、什么是系统的刚度矩阵?在结构动力学中,系统的刚度矩阵是一个方阵,它描述了系统对外部力的响应。
刚度矩阵的每个元素表示系统中某两个节点之间的刚度关系。
系统中的节点可以是结构的某些特定位置,比如梁的两个端点或支座的位置。
刚度矩阵中的元素通常是实数,表示两节点之间的刚度。
刚度矩阵的大小由系统中节点的数量决定。
对于一个具有n个节点的系统,刚度矩阵的大小将是n×n。
如果系统的每个节点都可以在某个方向上移动,那么刚度矩阵将是一个全阵。
如果某个节点不能在某个方向上移动,那么刚度矩阵的对应元素将为零。
二、如何推导系统的刚度矩阵?在推导系统的刚度矩阵时,我们需要考虑结构的材料特性、几何形状以及边界条件等因素。
下面是一般情况下推导系统刚度矩阵的步骤:1. 确定系统中的节点和每个节点之间的连接关系。
节点可以是结构的某些特定位置,如梁的两个端点或支座的位置。
连接关系包括节点之间的几何连接和约束条件。
2. 根据材料性质和结构几何形状,计算每个单元的刚度矩阵。
在结构中,通常将结构划分为若干个离散的单元。
每个单元的刚度矩阵由其材料性质、几何形状和约束条件等决定。
3. 将每个单元的刚度矩阵组合成整个系统的刚度矩阵。
这可以通过对单元刚度矩阵进行组装和连接操作来实现。
组装过程中要考虑每个单元在整个系统中的位置和连接关系。
4. 根据边界条件和外部力的施加情况,对刚度矩阵进行修正。
边界条件包括固定节点和受力节点等。
修正后的刚度矩阵将更准确地描述系统对外部力的响应。
三、系统的刚度矩阵有什么应用?系统的刚度矩阵在工程问题的分析和求解中有广泛的应用。
以下是一些常见的应用场景:1. 结构分析:刚度矩阵可用于分析结构的稳定性和振动特性。
第三节 刚度矩阵——节点载荷与节点位移之间的关系一、 单元刚度矩阵1. 单元刚度矩阵xj单元e 是在节点力作用下处于平衡。
节点i 的节点力为{}Ti xiyi R R R ⎡⎤=⎣⎦ (i , j , m 轮换)则单元e 的节点力列阵为{}TeTT T mi jTxm ym xi yi xj yj R R R R R R R R R R ⎡⎤⎣⎦⎡⎤⎣⎦==单元应力列阵为{}Tex y xy σσστ⎡⎤⎣⎦=假定弹性体的所有节点都产生一虚位移,单元e 的三个节点的虚位移为{}*******eT mm i i j ju v u v u v δ⎡⎤⎣⎦= 单元虚应变列阵为{}****Tx y xy εεεγ⎡⎤⎢⎥⎣⎦=参照式(3-7),则单元虚应变为{}{}**eeB εδ⎡⎤⎣⎦=作用在弹性体上的外力在虚位移上所做的功为:{}{}*eTe R δ⎛⎫ ⎪⎝⎭单元内的应力在虚应变上所做的功为:{}{}*Te tdxdy εσ∆⎛⎫ ⎪⎝⎭⎰⎰根据虚位移原理,可得单元的虚功方程{}{}{}{}**eTTe e R tdxdy δεσ∆⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=⎰⎰或{}{}{}{}**eTTTe e B R tdxdy δδσ∆⎛⎫⎛⎫⎡⎤ ⎪ ⎪⎣⎦⎝⎭⎝⎭=⎰⎰故有{}{}eTB R tdxdy σ∆⎡⎤⎣⎦=⎰⎰将式(3-10)代入,的{}{}{}eeeTTD B D B R B B tdxdytdxdy δδ∆∆⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦==⎰⎰⎰⎰(3-27)简记为{}{}ee ek R δ⎡⎤⎣⎦= (3-29)--------上式表征单元节点力与节点位移之间的关系,称为单元刚度方程(单元平衡方程) 其中TeD B B k tdxdy ∆⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦=⎰⎰(3-28) ek ⎡⎤⎣⎦称之为单元刚度矩阵(简称为单刚),是66⨯矩阵。
如果单元的材料是均质的,矩阵D ⎡⎤⎣⎦中的元素也是常量,且在三角形常应变的情况下,矩阵B ⎡⎤⎣⎦中的元素也是常数,当单元的厚度也是常数时,注意到dxdy ∆=∆⎰⎰,于是单元刚度矩阵可简化为TeB D B t k ⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦∆= (3-30) 将单元刚度矩阵按节点号写成分块矩阵形式:66eii ij imji jj jm mm mimj kk k k k k k k k k ⨯⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦= (3-31)其中任一子块[]rs k (r ,s=i ,j ,m )是一个2×2子矩阵,为[][][][]Trsrs k B D B t =∆ (r ,s=i ,j ,m )(1)对于平面应力问题将[]B 和平面应力问题的弹性矩阵[]D 代入,得Trs r s k B D B t ⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦=∆ ()21122114122r s r s r s r s r s r s r s r s b b c c b c c b Et c b b cc c b b μμμμμμμ--⎡⎤++⎢⎥=⎢⎥---∆⎢⎥++⎢⎥⎣⎦(r ,s=i ,j ,m ) (3-32)(2)对于平面应变问题将[]B 和平面应变问题的弹性矩阵[]D 代入,得()()()()()()()12122112114112121212121e rs k b b c c b c c b r s r s r s r s E t c b b c c c b b r s r s r s r sμμμμμμμμμμμμμμμ⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦--++----=+-∆--++--- (r,s=i ,j ,m ) (3-33)(注:是将式(3-32)中的,E μ分别换成21E μ- 和1μμ-)2. 单元刚度矩阵的性质 (1)ek ⎡⎤⎣⎦的物理意义式(3-29)可完整写为131415161112212223242526333435363132434445464142555152535456616263646i i jjmmeU k k k k k k V k k k k k k k k k k U k k k k k k k k V k k k k k k U k k k k k V⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=⎧⎫⎪⎪⎪⎪⎪⎪⎨⎬⎪⎪⎪⎪⎪⎪⎩⎭566ii j j m m eu v u v u k v ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎢⎥⎥⎣⎣⎦⎦⎧⎫⎪⎪⎪⎪⎪⎪⎨⎬⎪⎪⎪⎪⎪⎪⎩⎭可见每个节点在x 和y 方向上有二个平衡方程,3个节点共有六个平衡方程。
单元刚度矩阵[]ek 中的任一元素称为刚度系数,其物理意义为:ij k -----当单元的第j 个节点有单位位移,而其它节点位移为零时,需在单元第i 个节点位移方向上施加的节点力的大小。
例如, 23k 表示是第3个节点有水平(x )方向单位位移(即31u =)时,而其它节点位移分量均为零时,在第2个节点所引起的铅垂(y )方向的节点力。
(2)单元刚度矩阵只取决于单元形状,大小,方向和弹性常数,而与单元的位置无关。
即ek ⎡⎤⎣⎦不随单元坐标平移而改变,这叫单元刚度的平移原理。
235例如图示结构,有 [][](1)(3)k k = 另外,可以证明 [][](1)(2)B B=-则有 [][](1)(2)k k =即单元旋转180︒后,单元刚度矩阵相等。
这是单元刚度旋转原理。
(3) 单元刚度矩阵是对称矩阵。
因为 [][][]Tek B D B t ⎡⎤⎣⎦=∆所以有[]()[][][]()TTeTt k B D B =∆[][][]TTTTB D B t =∆⎡⎤⎣⎦[][][]TB D B t=∆e k ⎡⎤⎣⎦= (4)单元刚度矩阵是奇异矩阵。
即 0ek ⎡⎤⎣⎦=因为 {}[]{}ee e R k δ=当节点位移已知时,节点力是唯一确定的,而{}eR 已知时,{}e δ不能唯一确定,因为单元没有支承,可以产生任意的刚体位移。
根据上述性质:对于上图结构,在节点力为零时,单元仍可产生刚体位移,即0111213141516U k u k v k u k v k u k v i i i j j m m==+++++此时 0u u uu i j m=== ,0v v v v i j m === ,单元产生刚体位移0u ,0v 为任意的。
故有()()011131501214160k k k u k k k v +++++=由于,0u v 的任意性,则0111315k k k ++= , 0121416k k k ++=从而得0111315121416k k k k k k +++++= 同理可得:单元刚度矩阵任意一行(列)元素之和为零。
(5)单元刚度矩阵主对角线上的元素恒为正。
即 0(1,2,,6)ii k i >=二、 整体分析假设弹性体被分成m 个单元和n 个节点,对每一个单元进行前面的运算,则得到m 组型如{}{}e ee k R δ⎡⎤⎣⎦=的方程。
把这些方程集合起来,便可得到表征整体弹性体平衡的刚度方程:{}{}212122n n n n k R δ⨯⨯⨯⎡⎤⎢⎥⎣⎦= (3-37) 式中 1. {}21n δ⨯-------整体结构的节点位移列阵,是由各节点位移按节点号码从小到大顺序排列组成的,即{}12T T T T n δδδδ⎡⎤⎣⎦=其中 {}Ti ii u v δ⎡⎤⎣⎦= (i=1, 2,…,n )P 3P例如图示结构有{}123411223344TT T T T Tu v u v u v u v δδδδδ⎡⎤⎢⎥⎣⎦⎡⎤⎣⎦==2.{}21n R ⨯-------整体结构的节点载荷列阵, 是由各节点载荷按节点号码从小到大顺序排列组成的,即{}12T T TT n R R R R ⎡⎤⎣⎦=其中{}Ti ix iy R R R ⎡⎤⎢⎥⎣⎦= (i=1, 2,…,n )例如图示结构有{}11443124032T x y x y TT T T P P R R P R R R R R R R ⎡⎤⎣⎦⎡⎤=⎢⎥⎣⎦=--2. 22n nk ⨯⎡⎤⎢⎥⎣⎦-------整体结构的刚度矩阵(总刚)(1)22n nk ⨯⎡⎤⎣⎦的组集(“对号入座”法)22me n nek k ⨯⎡⎤⎡⎤⎢⎥⎣⎦⎣⎦=∑例图示结构有 单元1222421(1)424441121411ii ij imji jj jm mm mi mj k k k k k k k kk k k k k k k k k k k ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦==单元2444243(2)242223343233ii ij imji jj jm mm mi mj k k k k k k k kk k k k k k k k k k k ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦==注:在单元刚度矩阵中,各子块的下标表示该子块在总刚中的位置。
则总刚为(1)(1)(1)111214(1)(1)(2)(2)(1)(2)212222232424(2)(2)(2)323334(1)(1)(2)(2)(1)(2)4142424344448800k k k k k k k k k k k k k k k k k k k ⎡⎤⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦⨯++=++(2)总刚的性质 ⅰ. 整体刚度矩阵的物理意义[]K 中每一列元素的物理意义为:欲使弹性体的某一个节点在坐标轴方向发生单位位移,而其它节点都保持为零状态,在各节点上所需要加施加的节点力。
由式可以看出,令节点1在坐标轴x 方向有单位位移,即11u =,而其余的节点位移为零时,即v 1=u 2=v 2=u 3=v 3=······= u 2n =v 2n =0,这样就可得到节点载荷列阵等于总刚[]k 的第一列元素组成的列阵,即…………112211213141(21)1(2)1Tnxny x y x y Tn n R R R R R R K K K K K K ⎡⎤⎢⎥⎢⎥⎣⎦-⎡⎤⎣⎦=ⅱ. 总刚k ⎡⎤⎣⎦是对称矩阵 ⅲ. 总刚k ⎡⎤⎣⎦是奇异矩阵ⅳ. 总刚k ⎡⎤⎣⎦主对角线上的元素恒为正,即 0(1,2,,2)ii k i n >=ⅴ. 总刚[]k 是一个稀疏矩阵。
若遵守一定的节点编号规则,则非零元素集中在主对角线附近呈带状分布。