川师大学物理期末必考课后习题总结

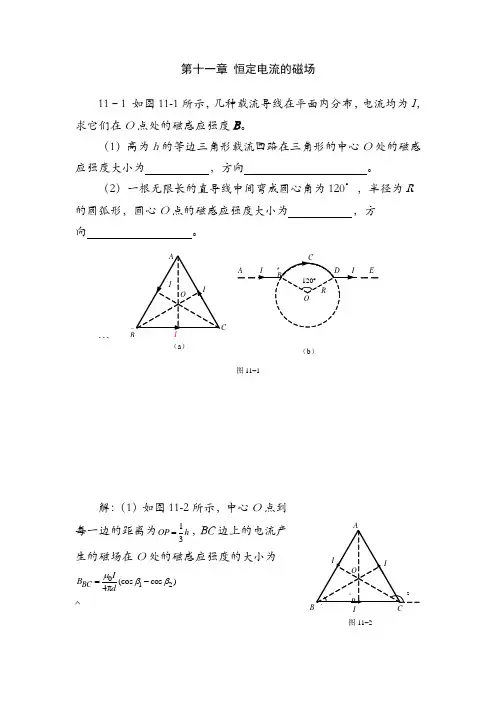
第十一章 恒定电流的磁场11–1 如图11-1所示，几种载流导线在平面内分布，电流均为I ，求它们在O 点处的磁感应强度B 。

（1）高为h 的等边三角形载流回路在三角形的中心O 处的磁感应强度大小为 ，方向 。

（2）一根无限长的直导线中间弯成圆心角为120°，半径为R 的圆弧形，圆心O 点的磁感应强度大小为 ，方向 。

…解：（1）如图11-2所示，中心O 点到每一边的距离为13OP h =，BC 边上的电流产生的磁场在O 处的磁感应强度的大小为012(cos cos )4πBC I B dμββ=-^IB21图11–2图11–1…B（a ）AE（b ）0(cos30cos150)4π/3Ih μ︒︒=-=方向垂直于纸面向外。

另外两条边上的电流的磁场在O 处的磁感应强度的大小和方向都与BC B 相同。

因此O 处的磁感应强度是三边电流产生的同向磁场的叠加，即3BC B B ===方向垂直于纸面向外。

（2）图11-1（b ）中点O 的磁感强度是由ab ，bcd ，de 三段载流导线在O 点产生的磁感强度B 1，B 2和B 3的矢量叠加。

由载流直导线的磁感强度一般公式012(cos cos )4πIB dμββ=- 可得载流直线段ab ，de 在圆心O 处产生的磁感强度B 1，B 3的大小分别为01(cos0cos30)4cos60)IB R μ︒=︒-︒π(0(12πI R μ=-031(cos150cos180)4πcos60IB B R μ︒==︒-︒0(12πI R μ=-】方向垂直纸面向里。

半径为R ，圆心角α的载流圆弧在圆心处产生的磁感强度的大小为04πI B Rμα=圆弧bcd 占圆的13，所以它在圆心O 处产生的磁感强度B 2的大小为00022π34π4π6II I B R R Rμμαμ===方向垂直纸面向里。

因此整个导线在O 处产生的总磁感强度大小为000012333(1)(1)0.212π22π26I I I I B B B B R R R Rμμμμ=++=-+-+=方向垂直纸面向里。

第一章质点运动学1、(习题1.1)：一质点在xOy 平面内运动，运动函数为2x =2t,y =4t 8-。

（1）求质点的轨道方程；（2）求t =1 s t =2 s 和时质点的位置、速度和加速度。

解：（1）由x=2t 得，y=4t 2-8可得：y=x 2-8即轨道曲线 （2）质点的位置：22(48)r ti t j =+- 由d /d vr t =则速度：28v i tj =+由d /d a v t =则加速度：8a j =则当t=1s 时，有24,28,8r i j v i j a j =-=+= 当t=2s 时，有48,216,8ri j v i j a j =+=+=2、（习题1.2）：质点沿x 在轴正向运动，加速度kv a -=，k 为常数．设从原点出发时速度为0v ，求运动方程)(t x x =.解：kv dtdv-=⎰⎰-=t v v kdt dv v 001t k e v v -=03、一质点沿x 轴运动，其加速度为a ?4t (SI)，已知t ?0时，质点位于x ??10m 处，初速度v ???0．试求其位置和时间的关系式．解：=a d v /d t 4=t d v 4=t d t ⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t2t t x txx d 2d 020⎰⎰=x 2=t 3/3+10(SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出，求：（1）小球的运动方程；（2）小球在落地之前的轨迹方程； （3d r ，d v ，解：（1）t v x 0=式（1）2gt 21h y -=式（2）201()(h -)2r t v t i gt j =+（2）联立式（1）、式（2）得22v 2gx h y -=（30d -gt rv i j =而落地所用时间gh 2t =0d -2gh r v i j =d v g j=-2202y2x)gt (v v v v -+=+=2120212202)2(2])([gh v gh g gt v tg dt dv +=+= 5、已知质点位矢随时间变化的函数形式为22r t i tj =+，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。

习 题 二2-1 质量为m 的子弹以速率0v 水平射入沙土中，设子弹所受阻力与速度反向，大小与速度成正比，比例系数为k ，忽略子弹的重力，求：(1)子弹射入沙土后，速度大小随时间的变化关系； (2)子弹射入沙土的最大深度。

[解] 设任意时刻子弹的速度为v ，子弹进入沙土的最大深度为s ，由题意知，子弹所受的阻力 f = - kv(1) 由牛顿第二定律 t v mma f d d == 即 tvm kv d d ==-所以 t m kv v d d -=对等式两边积分 ⎰⎰-=tv v t m k v v 0d d 0得 t mkv v -=0ln因此 t m kev v -=0(2) 由牛顿第二定律 x vmv t x x v m t v m ma f d d d d d d d d ==== 即 x vmv kv d d =-所以 v x mkd d =-对上式两边积分 ⎰⎰=-000d d v sv x m k得到 0v s mk-=-即 kmv s 0=2-2 质量为m 的小球，在水中受到的浮力为F ，当它从静止开始沉降时，受到水的粘滞阻力为f ＝kv (k 为常数)。

若从沉降开始计时，试证明小球在水中竖直沉降的速率v 与时间的关系为[证明] 任意时刻t 小球的受力如图所示，取向下为y 轴的正方向，开始沉降处为坐标原点。

由牛顿第二定律得即 tvm ma kv F mg d d ==--整理得mtkv F mg v d d =-- 对上式两边积分⎰⎰=--t vmt kv F mg v00d d得 mktF mg kv F mg -=---ln即 ⎪⎪⎭⎫ ⎝⎛--=-m kte kFmg v 1 2-3 跳伞运动员与装备的质量共为m ，从伞塔上跳出后立即张伞，受空气的阻力与速率的平方成正比，即2kv F =。

求跳伞员的运动速率v 随时间t 变化的规律和极限速率T v 。

[解] 设运动员在任一时刻的速率为v ，极限速率为T v ，当运动员受的空气阻力等于运动员及装备的重力时，速率达到极限。

液面下降的速度，即
，根据流量守恒
,
（2）当
（3）当
时，
时，
−
,整理可得：
可得
，即
,
图1-34所示为输液的装置。设吊瓶的截面积为1 ，针孔的截面积为2 ，且1 ≫ 2 ，开始时( = 0)，吊瓶内上下
液面距针孔的高度分别为ℎ1 和ℎ2 ，求吊瓶内药液全部输完时需要的时间。
，则针孔的流量为
液体总体积为
Ԧ =


= 2Ԧ − 2 Ԧ = −2Ԧ


1s末和2s末质点的速度为： 1 = 2Ԧ − 2Ԧ（m ∙ s−1 ），2 = 2Ԧ − 4Ԧ（m ∙ s −1 ）；
1s末和2s末质点的加速度相等：Ԧ = −2Ԧ （m ∙ s−2 ）
已知一质点做直线运动，其加速度Ԧ = 4 + 3 m ∙ s−2 , 开始运动时，0 = 5 m,



= 0.06（m）
（2）设弹簧最大压缩量为∆′ , 与碰撞粘在一起的速度为 ′，0 = ( +
) ′，代入已知条件可得 ′ = 4Τ11， + 压缩弹簧的过程中，机械能守恒，则
1
(
2
1
+ ) 2 = 2 ∆′2 ，得∆′ =
+


≈ 0.04（m）
(1)角加速度 =
由 =


∆
∆
=
0−2×1500÷60
50
由 =


=
2×1500
60
= 50 (rad ∙ s −1 )
= − (rad ∙ s−2 )
= −，得 = −，两边进行积分
得到 − 50 = − − 0,

某点的弧长 v0 ， b 都是常量，求：(1) t 时刻质点的加速度；(2) t 为何值时，加速度在数
值上等于 b 。
解：（1）
v
ds dt
v0
bt
a
dv dt
b
an
v2 R
(v0
bt)2 R
则
a
a2 an2
b2 (v0 bt)4 R2
加速度与半径的夹角为
(2)由题意应有
arctan a an
(6) 一质点沿半径为 R 的圆周作匀速率运动，每 t 秒转一圈，在 2t 时间间隔中，其
平均速度大小和平均速率大小分别为（答案：B）
(A) 2R , 2R tt
(B) 0, 2R t
(C) 0,0
(D) 2R ,0 t
1.2 填空题
(1) 一质点，以 m / s 的匀速率作半径为 5m 的圆周运动，则该质点在 5s 内，位
(4) 质点作变速曲线运动时，其切向加速度、法向加速度及加速度均不为零。
1.6 r 与 r 有无不同? dr 和 dr 有无不同? dv 和 dv 有无不同?其不同在哪
dt dt
dt dt
里?试举例说明。
解：（1） r
是位移的模， r 是位矢的模的增量，即 r
r2 r1
， r
r2
r1
；
（2） dr 是速度的模，即 dr v ds .
dt
dt
dt
dr 只是速度在径向上的分量. dt ∵有 r r rˆ （式中 rˆ 叫做单位矢），则 dr d r rˆ r drˆ
dt dt dt 式中 dr 就是速度在径向上的分量，
dt
∴ dr 与 d r 不同如题 1.6 图所示. dt dt

详细描述
通过解析力学习题，学生可以加深对力的理解，掌握力的 合成与分解的方法，以及运用牛顿运动定律解决实际问题。
举例
一质量为m的物体在几个共点力作用下处于平衡状态，若 撤去一个向东的恒力F，物体将产生向西的加速度，大小 为a。要求出其他所有力的合力大小及方向。
电磁学习题解析
总结词
理解电场、磁场的基本性质，掌 握电磁感应定律等。
详细描述
掌握牛顿运动定律的基本概念，理解力和加速度的关系，能够应用牛顿运动定律解决直线运动和曲线 运动的问题。了解动量守恒定律和角动量守恒定律，掌握它们在碰撞、抛体运动等场景中的应用。
力学基础
总结词
理解万有引力定律和天体运动的基本规 律。
VS
详细描述
掌握万有引力定律的基本概念，理解天体 之间的相互作用力，能够应用万有引力定 律解决天体运动的问题。了解开普勒三定 律，掌握行星、卫星等天体的运动规律。
注重解题方法
在解题时，要掌握多种解题方法，学会灵活运用。同时， 要注意解题的规范性和准确性，培养良好的解题习惯。
持续学习与提高
大学物理是一门不断发展的学科，新的理论和技术不断涌 现。要保持持续学习的态度，关注学科前沿动态，不断提 升自己的学术水平和综合素质。
THANKS FOR WATCHING
感谢您的观看
阻器、电容器、电感器等基本元件的特性和应用。
光学基础
总结词
理解光的干涉、衍射和偏振现象及其在现代光学 技术中的应用。
总结词
理解光电效应和光的量子性在光学技术中的应用 。
详细描述
掌握光的干涉、衍射和偏振的基本原理，理解干 涉条纹的形成和分布，能够应用这些原理解决光 学问题。了解光学仪器的基本原理和应用，如透 镜、棱镜等。

第一章 质点运动学1-1 一质点沿x 轴运动的规律是m t t x 542+-=，求前3s 它的位移和路程。

解：由042=-==t dt dxv 0/22>==s m dtdv a得质点做匀加速运动，在s t p 2=时运动方向改变。

0=t 时，()m x 50=s t 2=时，()m x 15842=+-=〔如图习题1-1解答图〕， s t 3=时，()m x 251293=+-=。

那么时间s 2~0质点的位移为()()m x x x 451021-=-=-=∆时间s 3~2质点的位移为()()m x x x 112232=-=-=∆前3s 它的路程m x x S 51421=+=∆+∆=前3s 它的位移m x x x 31421-=+-=∆+∆=∆习题1-1解答图a11-3 一质点的运动方程为m j t i t r 32+=。

求s t 1=时的速度、s 3~1的平均速度和平均加速度。

解：质点的速度矢量为s m j t i dtr d v /62+==s t 1=时的速度为s m j i j t i v s t s t /66121 +=+===。

s 3~1的平均速度为()()s m j i j i j i j i r r v st s t /262522225431313+=+=+-+=--===s 3~1的平均加速度为()()213/24265413sm j j i j i vv a s t s t=+-+=--===1-7 一质点沿半径为m 1的圆周运动，运动方程为rad t 332+=θ。

求s t 2=时，质点的切向角速度和法向加速度。

解：质点的角速度为29t dtd ==θω 质点的速度为R t R v 29==ω那么质点的切向加速度为tR dtdva t 18==质点的法向加速度为R t R a n 4281==ω故，s t 2=时，质点的切向加速度为222/36121818s m tR a s t st t=⨯⨯====法向加速度为24242/1296128181s m R t a s t st n=⨯⨯====第二章 牛顿运动定律2-1 质量为kg m 25.0=的质点，受力N i t F =的作用，0=t 时该质点以s m j v /2=的速度通过坐标原点。

习 题 十 三13-1 求各图中点P 处磁感应强度的大小和方向。

[解] (a) 因为长直导线对空间任一点产生的磁感应强度为：()210cos cos 4θθπμ-=aIB 对于导线1：01=θ，22πθ=，因此aI B πμ401=对于导线2：πθθ==21，因此02=BaIB B B πμ4021p =+= 方向垂直纸面向外。

(b) 因为长直导线对空间任一点产生的磁感应强度为：()210cos cos 4θθπμ-=aIB 对于导线1：01=θ，22πθ=，因此r I a I B πμπμ44001==，方向垂直纸面向内。

对于导线2：21πθ=，πθ=2，因此rI a I B πμπμ44002==，方向垂直纸面向内。

半圆形导线在P 点产生的磁场方向也是垂直纸面向内，大小为半径相同、电流相同的圆形导线在圆心处产生的磁感应强度的一半，即rIr I B 4221003μμ==，方向垂直纸面向内。

所以，rIr I r I r I r I B B B B 4244400000321p μπμμπμπμ+=++=++=(c) P 点到三角形每条边的距离都是a d 63=o 301=θ，o 1502=θ每条边上的电流在P 点产生的磁感应强度的方向都是垂直纸面向内，大小都是()aI d IB πμπμ23150cos 30cos 400000=-=故P 点总的磁感应强度大小为aIB B πμ29300== 方向垂直纸面向内。

13-2 有一螺线管长L ＝20cm ，半径r =2.0cm ，导线中通有强度为I =5.0A 的电流，若在螺线管轴线中点处产生的磁感应强度B ＝310166-⨯.T 的磁场，问该螺线管每单位长度应多少匝?[解] 已知载流螺线管轴线上场强公式为()120cos cos 2θθμ-=nIB由图知： 10410cos 2=θ，10410cos 1-=θ，所以，⎪⎪⎭⎫ ⎝⎛⨯=10410220nI B μ， 所以，匝＝1000101040IBn μ=13-3 若输电线在地面上空25m 处，通以电流31081⨯.A 。

大学物理课后答案详解第一章：力学1.1 牛顿定律的三种形式第一种形式：惯性定律牛顿的第一定律，也被称为惯性定律。

它的表述为：一个物体如果没有外力作用，将保持静止或匀速直线运动的状态。

这意味着在没有外力作用时，物体的加速度为零，速度保持不变。

这个定律的重要性在于它说明了运动的惯性特性。

举个例子，当我们在车上紧急刹车时，我们的身体会有向前的惯性，因为车突然减速，而我们的身体仍保持原来的运动状态。

第二种形式：动量定律牛顿的第二定律，也被称为动量定律。

它的表述为：一个物体的加速度正比于作用在它上面的合外力，反比于物体的质量。

通过数学表达式可以得到 F = ma，其中 F表示物体所受合外力的大小，m表示物体的质量，a表示加速度。

这个定律说明了力是一种导致物体加速度变化的物理量。

第三种形式：作用与反作用定律牛顿的第三定律，也被称为作用与反作用定律。

它的表述为：如果物体A对物体B施加了一个力，那么物体B对物体A也会施加一个大小相等、方向相反的力。

这一个定律解释了为什么当我们敲击桌子时，手感到疼痛，因为我们的手会受到桌子的反作用力。

同样地，当我们踢足球时，脚球会受到我们脚的力的影响而向前踢出。

1.2 动力学动力学是力学的一个重要分支，它研究的是物体在受力作用下的运动规律。

其中最常见的运动学参数有位移、速度和加速度。

1.2.1 位移位移是一个矢量量，它表示物体从初始位置到最终位置的改变。

位移的大小等于物体在运动过程中实际移动的距离。

位移的方向由初始位置和最终位置的连线所决定。

1.2.2 速度速度是一个矢量量，它表示物体单位时间内移动的位移。

速度的大小等于单位时间内移动的位移，而速度的方向由位移的方向和时间的方向所决定。

1.2.3 加速度加速度是一个矢量量，它表示单位时间内速度的变化量。

加速度的大小等于单位时间内速度的改变量，而加速度的方向由速度的方向和时间的方向所决定。

1.3 弹力和重力1.3.1 弹力弹力是一种垂直于两个物体接触面的力，它是由于两个物体之间的接触而产生的。

《大学物理学》课后习题参考答案习题11-1. 已知质点位矢随时间变化函数形式为)ωｔsin ωｔ(cos j i R r其中为常量．求：（1）质点轨道；(2)速度和速率。

解：1）由)ωｔsin ωｔ(cos j i R r知t cos R x ωtsin R yω消去t 可得轨道方程222Ryx2）jr vt Rcos sin ωωt ωR ωdtd iRωt ωR ωt ωR ωv2122])cos ()sin [(1-2. 已知质点位矢随时间变化的函数形式为j ir )t 23(t 42，式中r 的单位为m ，t 的单位为s .求：（1）质点的轨道；（2）从0t到1t 秒的位移；（3）0t 和1t 秒两时刻的速度。

解：1）由j ir)t 23(t 42可知2t 4x t23y消去t 得轨道方程为：2)3y(x2）jir v 2t 8dtd jij i v r 24)dt2t 8(dt101Δ3）jv 2(0)jiv 28(1)1-3. 已知质点位矢随时间变化的函数形式为j ir t t 22，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。

解：1）ji r v2t 2dtd iv a2dtd 2）212212)1t(2]4)t 2[(v1tt 2dtdv a 2t22221nta aat 1-4. 一升降机以加速度a 上升，在上升过程中有一螺钉从天花板上松落，升降机的天花板与底板相距为d ，求螺钉从天花板落到底板上所需的时间。

解：以地面为参照系，坐标如图，升降机与螺丝的运动方程分别为20121att v y （1）图 1-420221gttv h y （2）21y y （3）解之2d tg a 1-5. 一质量为m 的小球在高度h 处以初速度0v 水平抛出，求：（1）小球的运动方程；（2）小球在落地之前的轨迹方程；（3）落地前瞬时小球的td dr ，td dv ，tv d d .解：（1）t v x 0式（1）2gt21hy 式（2）jir )gt 21-h (t v (t)20（2）联立式（1）、式（2）得22v 2gx hy （3）ji r gt -v td d 0而落地所用时间gh 2t所以j i r 2gh -v t d d 0jv g td d 2202y2x)gt (vvvv 211222222[()](2)g ghg t dv dtvgt vgh 1-6. 路灯距地面的高度为1h ，一身高为2h 的人在路灯下以匀速1v 沿直线行走。

a gj 解：v v0 i gtj 方法1：速率 v v 2 ( gt ) 2 0
dv a dt
g 2t
2 v0 ( gt ) 2
v 方法2：切向单位矢量 v
切向加速度大小 a a gj
将
v0 30m s
v0 i gtj
2 v0 ( gt ) 2

V
0
L 1 V dV g sin xdx a L
g V sin ( L2 a 2 ) 积分得 L
2
V
g sin ( L2 a 2 ) L
12.质量为 m的物体最初位于 x0处，在力 F k / x 2 作用下由 静止开始沿直线运动，试证它在x处的速度为
1 x 2 ( y gt 2 ) (v0 t ) ,与 可得到 2
1 2 y v0 t sin 2 gt 2
角无关，任一时刻，它
1 2 们都在半径为 v0 t ,圆心为（0，- gt ）的圆周上。 2
v b R 的圆周按规律 S v0t bt 2 运动， 0， 都 6.一质点沿半径为
dx v0 dt
dl v dt
橇的速率
人的速率 x v0t
对（1）式求导 2l dl 2 x dx ,

v
2 v0 t 2
dt
dt
dl x v v0 dt l
(v0 t ) ( H h)
2
,雪橇运动方向与
x正方向相同
3.一球以30ms -1的速率水平抛出，求5s 后的切向加速度和法向 加速度。
V
2K 1 1 2K 1 1 2K 1 1 V ( ) ( )；V0 ( ) m x0 x m x x0 m x x0

大学物理期末重点回顾与总结近来，大学物理期末考试即将到来，本文将对整个学期的课程内容进行回顾与总结。

旨在帮助同学们回顾所学知识，巩固基本概念，并对重点难点进行强化学习，以期在考试中取得良好成绩。

下面将分为四个部分进行回顾与总结：力学、热学、光学和电磁学。

一、力学1.运动学与动力学运动学研究物体的运动规律，动力学则研究物体运动的原因。

本学期我们学习了位移、速度、加速度等运动学概念，并学习了牛顿定律和力的合成等动力学知识。

2.牛顿定律与力的合成牛顿第一定律指出物体在不受力的作用下，将保持静止状态或匀速直线运动。

牛顿第二定律是一个重要的动力学公式，表示物体的加速度与作用于其上的合外力成正比，与物体的质量成反比。

力的合成则指多个力合成一个力的过程，可以通过矢量的几何方法或合力分解的方法来求解。

3.重要概念与公式回顾在力学部分，同学们需要重点回顾质点的受力分析、动能和势能的转化、质点的圆周运动和万有引力等重要概念与公式。

二、热学1.温度与热量热学是研究物体的热现象和热力学定律的科学。

本学期我们学习了温度、热量和内能的概念，并了解了热传导、热辐射和热对流等热传递方式。

2.理想气体与状态方程理想气体是指具有非常小的分子体积和相互间无相互作用力的气体。

我们学习了理想气体的状态方程，即气体的温度、压力和体积之间的关系。

同时，还需要掌握理想气体的其他重要性质，如压强、摩尔质量和宏观系统中理想气体的内能等。

3.热力学第一和第二定律热力学第一定律是能量守恒定律的热学表达形式，指出能量可以互相转化，但总能量守恒。

热力学第二定律则是描述热现象方向性的定律，指出自然界中热量只能从热量高的物体传递到热量低的物体。

三、光学1.光的性质和光学仪器本学期我们学习了光的直线传播、折射、反射和干涉等基本性质，并了解了光的波粒二象性。

同时，还学习了光学仪器的工作原理，如凸透镜和凹透镜。

2.光的衍射和偏振衍射是指光通过透过孔径或障碍物时的传播现象，偏振则指光只在某个特定平面上振动。

大学物理期末课后习题参考答案第一章1.9 质点沿x 轴运动，其加速度和位置的关系为 a ＝2+62x ，a 的单位为2s m -⋅，x 的单位为 m. 质点在x ＝0处，速度为101s m -⋅,试求质点在任何坐标处的速度值． 解： ∵ xv v t x x v t v a d d d d d d d d ===分离变量： 2d (26)d v v adx x x ==+ 两边积分得c x x v ++=322221 由题知，0=x 时，100=v ,∴50=c∴ 13s m 252-⋅++=x x v1.10 已知一质点作直线运动，其加速度为 a ＝4+3t 2s m -⋅，开始运动时，x ＝5 m ，v =0，求该质点在t ＝10s 时的速度和位置． 解：∵ t tva 34d d +==分离变量，得 t t v d )34(d += 积分，得 12234c t t v ++= 由题知，0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量， t t t x d )234(d 2+=积分得 232212c t t x ++=由题知 0=t ,50=x ,∴52=c 故 521232++=t t x所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1.11 一质点沿半径为1 m 的圆周运动，运动方程为 θ=2+33t ，式中θ以弧度计，t 以秒计，求：(1) t ＝2 s 时，质点的切向和法向加速度；(2)当加速度的方向和半径成45°角时，其角位移是多少?解： t tt t 18d d ,9d d 2====ωβθω (1)s 2=t 时， 2s m 362181-⋅=⨯⨯==βτR a2222s m 1296)29(1-⋅=⨯⨯==ωR a n(2)当加速度方向与半径成ο45角时，有145tan ==︒na a τ即 βωR R =2亦即 t t 18)9(22= 则解得 923=t 于是角位移为322323 2.67rad 9t θ=+=+⨯=第二章2.9 质量为16 kg 的质点在xOy 平面内运动，受一恒力作用，力的分量为x f ＝6 N ，y f ＝-7 N ，当t ＝0时，==y x 0，x v ＝-2 m ·s -1，y v ＝0．求当t ＝2 s 时质点的(1)位矢；(2)速度．解： 2s m 83166-⋅===m f a x x2s m 167-⋅-==mf a y y (1)21021035'22m s 8477'2m s 168x x x y y y v v a dt v v a dt --=+=-+⨯=-⋅-=+=⨯=-⋅⎰⎰于是质点在s 2时的速度1s m 8745-⋅--=ji v(2)2211()221317(224)()428216137m48x x y r v t a t i a t ji j i j =++-=-⨯+⨯⨯+⨯=--2.18 以铁锤将一铁钉击入木板，设木板对铁钉的阻力与铁钉进入木板内的深度成正比，在铁锤击第一次时，能将小钉击入木板内1 cm ，问击第二次时能击入多深，假定铁锤两次打击铁钉时的速度相同．题2.18图解: 以木板上界面为坐标原点，向内为y 坐标正向，如题2.18图，则铁钉所受阻力为ky f -=第一锤外力的功为1A⎰⎰⎰==-='=ssky ky y f y f A 112d d d ① 式中f '是铁锤作用于钉上的力，f 是木板作用于钉上的力，在0d →t 时，f 'f -=． 设第二锤外力的功为2A ，则同理，有⎰-==21222221d y kky y ky A ② 由题意，有2)21(212kmv A A =∆== ③即 222122kk ky =-所以， 22=y于是钉子第二次能进入的深度为cm 414.01212=-=-=∆y y y2.22 如题2.22图所示，一物体质量为2kg ，以初速度0v ＝3m ·s -1从斜面A 点处下滑，它与斜面的摩擦力为8N ，到达B 点后压缩弹簧20cm 后停止，然后又被弹回，求弹簧的劲度系数和物体最后能回到的高度．题2.22图解: 取木块压缩弹簧至最短处的位置为重力势能零点，弹簧原长处为弹性势能零点。

B . 2n 2e -仁 2n 11入射光n 1反射光2第十三章光的干涉13-在双缝干涉实验中，两缝分别被折射率为n i 和n 2的透明薄膜遮盖，二者的厚度均为 e ,波长为入的平行单色光垂直照射到双缝上，在屏中央处，两束相干光的位相差 __________________ 。

解：加入透明薄膜后，两束相干光的光程差为n i e -2e ，则位相差为2 2(n 〔e ^e) (n 〔 n 2)e13-2如图13-1所示，波长为入的平行单色光垂直照射到两个劈尖上，两劈尖角分别为1和 2，折射率分别为 n 1和n 2，若二者分别形成的干涉条纹的明条纹间距相等，则1, 2，n 1和n 2之间的关系是 _______________ 。

解：劈尖薄膜干涉明条纹间距为L（ 很小）2nsin 2n两劈尖干涉明条纹间距相等，所以2门1 1 2n 2 2n1 1 n2 2 或 1 2 n 2 山13-3用一定波长的单色光进行双缝干涉实验时，欲使屏上的干涉条纹间距变大，可采用的方法解：因为干涉条纹的间距与两缝间距成反比，与屏与双缝之间的距离成正比。

故填“使两缝间距 变小；使屏与双缝之间的距离变大。

13-4用波长为 入的单色光垂直照射如图 13-2示的劈尖膜(n 1 > n 2 > n 3)，观察反射光干涉，从 劈尖顶开始算起，第 2条明条纹中心所对应的膜厚度 e = _______ 。

解：劈尖干涉(n 1> n 2> n 3)从n 1射向n 2时无半波损失， 产生明条纹的条件为2n 2e = k ， k = 0,1,2,3 … 在e = 0时，两相干光相差为 0,形成明纹。

第2条明条纹中心所对应的膜厚度为k = 1,即2n 2e =，则e ——2n 20.620mm 的过程中，观察到干涉条纹移动了 2300e ，对应于可动反射镜的移动， 干涉条纹每移动一条，厚度变化 —，现移动2300条，厚度变化e 2300 — 0.620mm ，则 =。

根据匀加速直线运动的速度公 式$v = v_0 + at$，代入已知的 $v_0 = 2m/s$和$a = 3m/s^2$，以及时间$t = 3s$， 计算得到$v = 2m/s + 3 times 3m/s^2 = 11m/s$。
一物体做匀减速直线运动，初 速度为10m/s，加速度为2m/s^2，则该物体在速度减为 零时的位移是多少？
04
答案解析
根据公式$v = lambda f$，频率$f = frac{v}{lambda} = frac{3 times 10^{8}}{500 times 10^{-9}}Hz = 6 times 10^{14}Hz$；根据公式 $E = hnu$，能量$E = h times f = 6.626 times 10^{-34} times 6 times
题目
答案解析
计算氢原子光谱线波长与频 率的关系。
根据巴尔末公式，氢原子光 谱线波长与频率的关系可以
表示为λ=R*(1/n1^2 1/n2^2)，其中λ是光谱线波 长，R是里德伯常数，n1和 n2分别是两个能级的主量子
数。
பைடு நூலகம்
题目
一束光照射到某金属表面， 求光电子的最大初动能。
答案解析
根据爱因斯坦光电效应方程，光 电子的最大初动能Ekm=hν-W， 其中h是普朗克常数，ν是入射光 的频率，W是金属的逸出功。因 此，通过测量入射光的频率和金 属的逸出功，可以计算出光电子
题目
一定质量的理想气体，在等容升温过 程中，不吸热也不放热，则内能如何 变化？
答案解析
根据热力学第一定律，等容升温过程 中，气体不吸热也不放热，则内能增 加。
热传递习题及答案解析
题目

第五章 机械振动5–1 在两个相同的弹簧下各悬一物体，两物体的质量比为4:1，则二者作简谐振动的周期之比为_________。

解：由弹簧振子的周期公式kmT π2=可得，二者的周期之比为2:1。

5–2 某星球质量是地球质量的P 倍，半径是地球半径的q 倍，一只在地球上周期为T 的单摆在该星球上的振动周期为 。

解：因e s pM M =，e s qR R =，所以星球上的重力加速度为g qp R q pM GR M Gg 22s2e2sss ===星球上该单摆的振动周期为T Pq g l T ==s s π2 5–3 一汽车载有四人，他们的质量共为250kg ，上车后把汽车的弹簧压下5×10-2m 。

若该汽车弹簧共负载1000kg 的质量，则汽车的固有频率为 。

解：由题意可得弹簧的劲度系数为42109.41058.9250⨯=⨯⨯==-x mg k N/m 负载M =1000kg 的质量时，汽车的固有频率为π271000109.4π21π21π24=⨯===M k ωνHz 5–4 一弹簧振子，当t =0时，物体处在平衡位置且向x 正方向运动，则它的振动的初相位为 。

解：将0=t 时，0=x ，代入振动方程)(cos ϕω+=t A x ，得ϕcos 0A =，故2π-=ϕ或2π 又由于0=t 时，物体向x 正方向运动，即0>v ，即需0sin >-=ϕωA x ，故初相位为2π-=ϕ5–5 一简谐振动方程为)3cos(ϕ+=t A x ，已知t = 0时的初位移为0.04m ，初速度为0.09 m/s ，则振幅A =________，初相ϕ =_____________。

解：振幅223222202010509.004.0-⨯=+=+=ωv x A m初相)43arctan()04.0309.0arctan()arctan(00-=⨯-=-=x ωϕv 5–6 一简谐振动的旋转矢量图如图5-1所示，振幅矢量长2cm ，则该简谐振动的初相为______。