线路中桩坐标计算

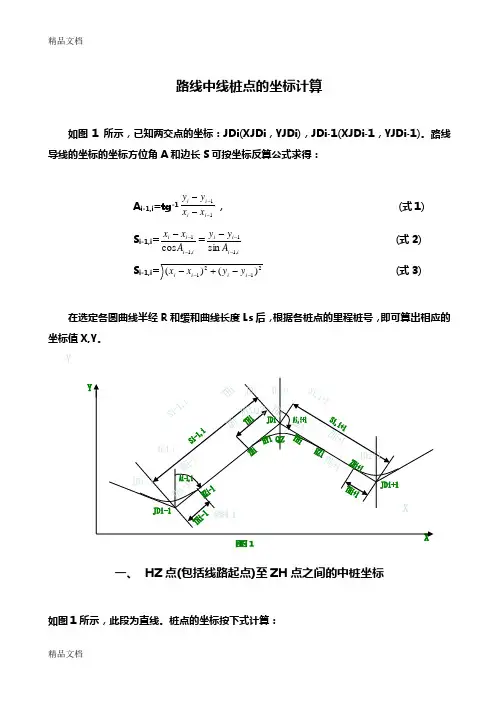
线路中桩坐标计算ZX点L i=T+（JSLCZ-HZLC）X i=X JD+Li*COS﹫JD-HZY i=Y JD+Li*SIN﹫JD-HZZH点X ZH=X JD+T*COS﹫JD-ZHY ZH=Y JD+T*SIN﹫JD-ZHHZ点X HZ=X JD+T*COS﹫JD-HZY HZ= Y JD+T*SIN﹫JD-HZZH------HY HZ------YH 点切线点x i=L-L^5/40C^2y i=L^3/6CC=RL0统一点第一缓和曲线﹫ZH-i=﹫ZH-JD±arcTAN(y/x)D=(x^2+y^2)^1/2X i=X ZH+D*COS﹫ZiY i=Y ZH+D*SIN﹫Zi第二缓和曲线﹫HZ-i=﹫HZ-JD±arcTAN(y/x) +180°D=(x^2+y^2)^1/2X i=X HZ+D*COS﹫HiY i=Y HZ+D*SIN﹫HiHY------YH点切线点x i=R*SIN﹫+My i=R*（1-COS﹫C）+P﹫C=(180°*（L-L0）/3.1415926*R)+B0 B0=180°*L0/2×3.1415926*R统一点﹫Zi=﹫ZH-JD±arcTAN(y/x)D=(x^2+y^2)^1/2X i=X ZH+D*COS﹫ZiY i=Y ZH+D*SIN﹫Zi线路边桩坐标计算ZX点﹫左=﹫JD-HZ-90°﹫右=﹫JD-HZ-90°X 左=X JSLCZ+D左*COS﹫左Y左=Y JSLCZ+D左*SIN﹫左X右=X JSLCZ+D右*COS﹫右Y 右=Y JSLCZ+D右*SIN﹫右ZH------HY HZ------YH 点第一缓和曲线B P=((L^2)/2*R*L0)*(180°/3.1415926)﹫左=﹫ZH-JD-B P-90°﹫右=﹫ZH-JD-B P+90°X 左=X JSLCZ+D左*COS﹫左Y左=Y JSLCZ+D左*SIN﹫左X右=X JSLCZ+D右*COS﹫右Y 右=Y JSLCZ+D右*SIN﹫右第二缓和曲线B P=((L^2)/2*R*L0)*(180°/3.1415926)﹫左=﹫HZ-JD-B P-90°﹫右=﹫HZ-JD-B P+90°X 左=X JSLCZ+D左*COS﹫左Y左=Y JSLCZ+D左*SIN﹫左X右=X JSLCZ+D右*COS﹫右Y 右=Y JSLCZ+D右*SIN﹫右HY------YH点圆心坐标﹫JD-O=﹫JD-ZH+(180°-﹫)/2XO=X JD+(R+E)COS﹫JD-OYO=Y JD+(R+E)SIN﹫JD-O圆弧点坐标﹫左=﹫JD-O﹫右=﹫O-JD=﹫JD-O+180°X 左=X JSLCZ+D左*COS﹫左Y左=Y JSLCZ+D左*SIN﹫左X右=X JSLCZ+D右*COS﹫右Y 右=Y JSLCZ+D右*SIN﹫右线路各点方位角计算β0= (L0/(2*R))*(180/3.1415926)βi =(L i^2/2/R/L0)*(180/3.1415926)φi=(L i/R)*(180/3.1415926) ( 圆曲线)ZH-------HY点αi=αZH-JD+βi (右“+”左“-”)YH-------HZ点αi=αJD-HZ-βi () (右“-”左“+”)HY-------QZ 点αi=αZH-JD+βi +φi () (右“+”左“+”)QZ-------YH点αi=αJD-HZ-βi -φi () (右“-”左“-”)。

高等级公路中桩边桩坐标计算方法一、平面坐标系间的坐标转换公式如图 9 .设有平面坐标系 xoy 和 x'o'y' （左手系—— x 、 x' 轴正向顺时针旋转90°为 y 、 y' 轴正向）； x 轴与 x' 轴间的夹角为θ（ x 轴正向顺时针旋转至 x' 轴正向.θ范围：0° —360°）。

设 o' 点在 xoy 坐标系中的坐标为（ xo',yo' ）.则任一点 P 在 xoy 坐标系中的坐标（ x,y ）与其在 x'o'y' 坐标系中的坐标（ x',y' ）的关系式为：二、公路中桩边桩统一坐标的计算（一）引言传统的公路中桩测设.常以设计的交点（ JD ）为线路控制.用转点延长法放样直线段.用切线支距法或偏角法放样曲线段；边桩测设则是根据横断面图上左、右边桩距中桩的距离（、）.在实地沿横断面方向进行丈量。

随着高等级公路特别是高速公路建设的兴起.公路施工精度要求的提高以及全站仪、 GPS 等先进仪器的出现.这种传统方法由于存在放样精度低、自动化程度低、现场测设不灵活（出现虚交.处理麻烦）等缺点.已越来越不能满足现代公路建设的需要.遵照《测绘法》的有关规定.大中型建设工程项目的坐标系统应与国家坐标系统一致或与国家坐标系统相联系.故公路工程一般用光电导线或 GPS 测量方法建立线路统一坐标系.根据控制点坐标和中边桩坐标.用“极坐标法”测设出各中边桩。

如何根据设计的线路交点（ JD ）的坐标和曲线元素.计算出各中边桩在统一坐标系中的坐标.是本文要探讨的问题。

（二）中桩坐标计算任何复杂的公路平面线形都是由直线、缓和曲线、圆曲线几个基本线形单元组成的。

一般情况下在线路拐弯时多采用“完整对称曲线”.所谓“完整”指第一缓和曲线和第二缓和曲线的起点（ ZH 或 HZ ）处的半径为∞ ；所谓“对称”指第一缓和曲线长和第二缓和曲线长相等。

线路逐桩坐标计算原理高等级公路、铁路的测设通常要用全站仪应用极坐标法测设中线，利用极坐标法测设中线就必须知道线路中线的点位坐标。

下面就有关计算原理进行说明。

直线段逐桩坐标计算原理直线是线路中最基本的线形。

直线以最短的距离连接两目的地，具有线路短捷，汽车行车方向明确，驾驶操作简单，视距良好等特点，同时直线线形简单也容易计算。

其计算方法和导线类似，知道一个已知点坐标，直线的方位角和距离（即历程差）就能计算未知点里程桩坐标。

如图2-1，例如已知直线A 点坐标和直线方位角AB α以及直线AB 之间的距离AB d 推算B 点坐标：图2-1直线线路⎭⎬⎫+=+=AB AB A B AB AB A B d Y Y d X X ααsin cos （2-1）圆曲线逐桩坐标计算原理铁路与公路线路的平面通常由直线和曲线构成，这是因为在线路的定线中，由于受地形、地物或其他因素限制,需要改变方向。

在改变方向处，相邻两直线间要求用曲线连结起来,以保证行车顺畅安全。

这种曲线称平面曲线。

由于受地形等条件限制，路线总是不断从一个方向转到另一个方向。

这时为了工程能 安全运营，必须用曲线来连接。

其中，圆曲线是最基本线路曲线之一，它是有一定曲率的圆弧。

下面介绍圆曲线的理论计算。

如图2-2所示，直线与圆曲线的连接点称为直圆点（ZY ）；圆曲线的中点称为曲线中点（QZ ）；圆曲线与直线的连接点称为圆直点（YZ ）。

圆曲线要素有线路转向角α，圆曲线半径R ，圆曲线长L ，外矢距E 及切曲差q 。

其中转向角α（单位：度、分、秒）和半径R 是已知数据，其余要素如切线长T ，曲线长L, 外矢距E, 切曲差q 可以按下列关系式计算得出：图2-2圆曲线⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫-=-⨯=⨯=⨯=LT q R E R L R T 2)12(sec1802tanαπαα （2-2） 1)曲线要素计算由交点里程、切线长T 和曲线长L 计算曲线主点里程：ZY 里程 = JD 里程 - 切线长TQZ 里程 = ZH 里程 + L/2YZ 里程 = ZY 里程 + 曲线长L2) ZY 点与YZ 点坐标计算由已知条件和计算出的曲线要素L T 、用极坐标法求出ZY 和YZ 点坐标。

路线中桩坐标的计算公式在道路建设和维护中，桩号是一个非常重要的概念。

它用来表示道路上的位置，帮助工程师和施工人员准确地定位和测量。

桩号通常是以公里为单位，每隔一定距离就会设置一个桩号，以便对道路进行定位和管理。

在本文中，我们将讨论路线中桩坐标的计算公式，以及如何使用这些公式进行实际测量和定位工作。

路线中桩坐标的计算公式通常涉及到道路的曲线和坡度等因素。

在实际测量中，通常会使用全站仪或者GPS等设备来测量各个桩号的坐标，然后根据这些坐标来计算出路线中桩的坐标。

下面我们将介绍几种常见的计算公式。

1. 直线路段的桩坐标计算公式。

在直线路段上，桩号和坐标的计算比较简单。

假设起点的坐标为(x1, y1)，终点的坐标为(x2, y2)，起点的桩号为P1，终点的桩号为P2。

那么在直线路段上任意一个桩号P的坐标可以通过如下公式计算得出：x = x1 + (x2 x1) (P P1) / (P2 P1)。

y = y1 + (y2 y1) (P P1) / (P2 P1)。

其中，x和y分别表示桩号为P时的坐标，P为需要计算坐标的桩号。

2. 曲线路段的桩坐标计算公式。

在曲线路段上，桩坐标的计算会更加复杂一些，需要考虑曲线的半径、圆心、圆心角等因素。

在实际测量中，通常会使用曲线表来进行计算。

曲线表是根据设计参数和曲线类型制定的一张表格，其中包含了各个桩号对应的曲线半径、圆心角等信息。

通过曲线表，可以根据桩号和曲线类型来计算出相应的曲线参数，进而得出桩坐标。

3. 坡度路段的桩坐标计算公式。

在坡度路段上，桩坐标的计算也需要考虑坡度的影响。

假设起点的坐标为(x1,y1)，终点的坐标为(x2, y2)，起点的桩号为P1，终点的桩号为P2，坡度为S。

那么在坡度路段上任意一个桩号P的坐标可以通过如下公式计算得出：x = x1 + (x2 x1) (P P1) / (P2 P1)。

y = y1 + (y2 y1) (P P1) / (P2 P1) + S (P P1)。

中桩坐标的计算一、测量坐标系统（一）大地坐标系统在大地坐标系中，地面点在地球表面上的投影位置用大地经度和大地纬度来表示，地面点的大地坐标是根据大地测量数据由大地坐标原点推算而得，我国大地坐标原点位于陕西泾阳县永乐镇境内，在西安市以北约40Km 处。

（二）高斯3°平面直角坐标系统我国从1952年开始采用高斯投影系统，以高斯投影的方法建立了高斯直角坐标系统。

地面点的高斯平面坐标与大地坐标可以相互转换。

高速公路的勘测设计和施工放样都采用高斯平面直角坐标系统进行的。

（三）平面直角坐标系统在测量范围较小、三级和三级以下公路、独立桥梁隧道及其它构造物，可以把该测区的球面当作平面看待进行直接投影，采用平面直角坐标系统。

二、中桩坐标计算（一）计算导线点的坐标1．方位角的确定：tg β=XY ∆∆ 方位角 : Ai =β （第一象限）Ai =180 °－β （第二象限）Ai =180° + β （第三象限）Ai =360° －β （第四象限）图 2—18 路线的方位角计算2．坐标计算：X i+1 = X i + D CosAiY i+1 = Yi + D SinAi (D ：两导线点间的水平距离)（二）计算中桩坐标１.未设缓和曲线的单圆曲线坐标计算（1）圆曲线起、终点坐标计算JDi 的坐标为（X JDi 、Y JDi ），交点前后直线边的方位角分别为A i -1、A i ，圆曲线的半径为R ，平曲线切线长为T i .,曲线起、终点的坐标可用下式计算：圆曲线起点的坐标： X ZYi = X JDi －T i CosA i -1 Y ZYi = Y JDi －T i SinA i -1圆曲线终点的坐标： X YZi = X Jdi + T i CosA i Y YZi = Y Jdi + T i SinA i图 2—19 中桩坐标计算示意图（2）圆曲线任意点坐标计算ZY ～ QZ 段（YZ ～QZ 段）的坐标计算以曲线起点ZY （曲线终点YZ 点）为坐标原点，切线为X ′轴，法线为Y ′轴，建立直角坐标系:X ′= R Sin(π180'R l ) Y ′= R －R Cos (π180'R l ) 式中： l ′———圆曲线上任意点至 ZY （YZ ）点的弧长；ZY ～QZ 段的各点的坐标：利用上述公式计算出以ZY 为坐标原点圆曲线段内各加桩X ′、Y ′ 的值，则ZY ～QZ 段的各点的坐标和方位角为：X = X ZYi - X ′ CosA i -1 – ζY ′sin A i -1Y = Y ZYi + X ′ SinA i -1 +ζY ′cos A i -1YZ ～QZ 段的各点的坐标：利用上述公式计算出以YZ 为坐标原点圆曲线段内各加桩X ′、Y ′ 的值，则ZY ～QZ 段的各点的坐标为：X= X YZi - X ′ CosA i –ζY ′Sin A iY= Y YZi - X ′ SinA i +ζY ′Cos A i式中：ζ — 路线转向，右转角时ζ=1，左转角时ζ= -1，以下各式同。

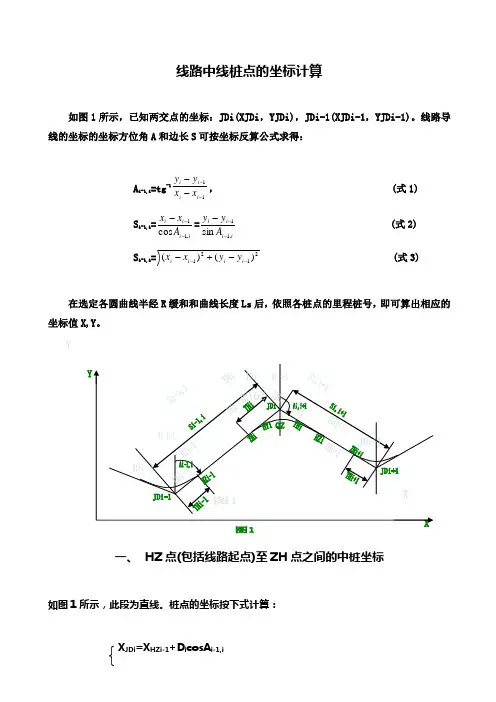
线路中线桩点的坐标计算如图1所示，已知两交点的坐标：JDi(XJDi ，YJDi)，JDi-1(XJDi-1，YJDi-1)。

线路导线的坐标的坐标方位角A 和边长S 可按坐标反算公式求得：A i-1,i =tg -111----i i i i x x y y ， (式1)S i-1,i =i i i i A x x ,11cos ---=ii i i A y y ,11sin --- (式2)S i-1,i =2121)()(---+-i i i i y y x x (式3)在选定各圆曲线半经R 缓和和曲线长度Ls 后，依照各桩点的里程桩号，即可算出相应的坐标值X,Y 。

一、 HZ 点(包括线路起点)至ZH 点之间的中桩坐标如图1所示，此段为直线。

桩点的坐标按下式计算：X JDi =X HZi-1+D i cosA i-1,iY JDi =Y HZi-1+D i sinA i-1,I (式4)式中A i-1,i 为线路导线JDi-1到JDi 的坐标方位角；Di 为桩点到HZi-1的距离(Si-1,i –THi-1)，即桩点里程与HZi-1点里程之差；X HZi-1、Y HZi-1为HZi-1点的坐标，由下式计算：XHZi-1=X JDi-1+T Hi-1cosA i-1,iY HZi-1=X JDi-1+T Hi-1sinA i-1,i (式5) 同理计算出直线终点ZHi 点的坐标 X ZHi =X JDi-1+(Si-1,i –THi)cosA i-1,iY ZHi =X JDi-1+(Si-1,i –THi)sinA i-1-I (式6)二、 ZH 点至YH 点之间的中桩坐标如图1所示,此段包括第一缓和曲线及圆曲线,先计算桩点的切线支距法坐标x 、y ：1、缓和曲线上桩点的切线支距法坐标x 、y ：X=()L -22540SL R L Y=SRL L 63(式7)L 为桩点(测点)到缓和曲线起点ZH 的曲线长，即测长；R 为圆曲线半径；L S 为缓和曲线总长2、圆曲线上桩点的切线支距法坐标x 、y ：以ZH 为起点：(带有缓和曲线的圆曲线，)X=Rsin ϕ+q=Rsin )2(1800S L L R +π+2S L –23240RL SY=R(1－cos ϕ)+p=R 〔1–cos )2(1800S L L R +π〕+RL S 242 (式8) ○1L 为桩点到HY(缓圆点,既圆曲线的起点)的曲线长，仅为圆曲线部份的长度，那么：式中ϕ=α+βo =RL π180⨯+βo =R L π0180⨯+πR L S 21800⨯=)2(1800S L L R +π， ○2假设L 为桩点到ZH(直缓点)的曲线长，那么：式中ϕ=α-βo =RL π180⨯-βo =R L π0180⨯-πR L S 21800⨯=)2(1800S L L R -π。

线路中边桩坐标计算通用公式
在进行线路中、边桩坐标计算时，可以使用以下通用公式：
1.线路中桩号计算公式：
桩号=起点桩号+距离
这个公式可以用来确定线路上其中一点的桩号，其中起点桩号是线路的开始处的桩号，距离是该点距离起点的距离。

2.边桩坐标计算公式：
(X,Y)=(X0+DX,Y0+DY)
在这个公式中，(X0,Y0)是线路上其中一起点边桩的坐标，DX和DY 分别是该边桩在水平和垂直方向上的偏移量。

通过这个公式，可以计算线路上任意一个边桩的坐标。

3.边桩水平距离计算公式：
D=√(DX^2+DY^2)
这个公式可以计算线路上两个边桩之间的水平距离，其中DX和DY是两个边桩在水平和垂直方向上的偏移量。

4.边桩偏角计算公式：
α = arctan(DY / DX)
在这个公式中，α表示边桩与起点边桩之间的偏角，DX和DY是两个边桩在水平和垂直方向上的偏移量。

这些公式可以在线路设计、测量、施工等方面使用，用于计算线路中其中一点的桩号、边桩的坐标、边桩之间的距离等。

通过这些计算，可以提高线路建设的精度和效率。

高等级公路中桩边桩坐标计算方法一、平面坐标系间的坐标转换公式如图 9 ，设有平面坐标系 xoy 和 x'o'y' （左手系—— x 、 x' 轴正向顺时针旋转90°为 y 、 y' 轴正向）； x 轴与 x' 轴间的夹角为θ（ x 轴正向顺时针旋转至 x' 轴正向，θ范围：0° —360°）。

设 o' 点在 xoy 坐标系中的坐标为（ xo',yo' ），则任一点 P 在 xoy 坐标系中的坐标（ x,y ）与其在x'o'y' 坐标系中的坐标（ x',y' ）的关系式为：二、公路中桩边桩统一坐标的计算（一）引言传统的公路中桩测设，常以设计的交点（ JD ）为线路控制，用转点延长法放样直线段，用切线支距法或偏角法放样曲线段；边桩测设则是根据横断面图上左、右边桩距中桩的距离（、），在实地沿横断面方向进行丈量。

随着高等级公路特别是高速公路建设的兴起，公路施工精度要求的提高以及全站仪、 GPS 等先进仪器的出现，这种传统方法由于存在放样精度低、自动化程度低、现场测设不灵活（出现虚交，处理麻烦）等缺点，已越来越不能满足现代公路建设的需要，遵照《测绘法》的有关规定，大中型建设工程项目的坐标系统应与国家坐标系统一致或与国家坐标系统相联系，故公路工程一般用光电导线或 GPS 测量方法建立线路统一坐标系，根据控制点坐标和中边桩坐标，用“极坐标法”测设出各中边桩。

如何根据设计的线路交点（ JD ）的坐标和曲线元素，计算出各中边桩在统一坐标系中的坐标，是本文要探讨的问题。

（二）中桩坐标计算任何复杂的公路平面线形都是由直线、缓和曲线、圆曲线几个基本线形单元组成的。

一般情况下在线路拐弯时多采用“完整对称曲线”，所谓“完整”指第一缓和曲线和第二缓和曲线的起点（ ZH 或 HZ ）处的半径为∞ ；所谓“对称”指第一缓和曲线长和第二缓和曲线长相等。

1. 直线上中桩坐标计算设交点坐标为JD （XJ,YJ ）,交点前后相邻直线的方位角分别为A 1、A 2，则ZH （或ZY ）点坐标：)180cos(1++=A T XJ X ZH)180s i n (1++=A T YJ Y ZH （1） HZ （或YZ ）点坐标：2cos A T XJ X HZ +=2s i n A T YJ Y HZ += （2） 设直线上加桩里程为L ，ZH 、HZ 表示曲线起、终点里程，则前直线上任意点坐标（L ≤ZH ）：)180cos()(1+⋅-++=A L ZH T XJ X)180sin()(1+⋅-++=A L ZH T YJ Y后直线上任意点坐标（L ＞ZH ）2cos )(A HZ L T XJ X ⋅-++=2sin )(A HZ L T YJ Y ⋅-++=2. 单曲线内中桩坐标计算（1）不设缓和曲线的单曲线由（1）、（2）计算，设曲线起、终点坐标分别为ZY （X zy ，Y zy ）、YZ （X zy ，Y yz ），则圆曲线上坐标为：)90cos()90sin(21Rl A R l R X X zy πξπ+⋅+= )90sin()90sin(21Rl A R l R Y Y zy πξπ+⋅+= 式中，l ------圆曲线内任意点至ZY 点的曲线长；R------圆曲线半径；ξ-----转角符号，右转为“+”、左转为“-”，以下公式中相同。

（2）设缓和曲线的单曲线缓和曲线上任意点的切线横距⋅⋅⋅⋅⋅⋅+-+-=6613449225599040345640S s s L R l L R l L R l l x式中：l ------缓和曲线上任意点至ZH （或HZ ）点的曲线长；L s ------缓和曲线长度；1） 第一缓和曲线（ZH —HY ）任意点坐标)30cos()30cos(/212ss ZH RL l A RL l x X X πξπ+⋅+= )30sin()30cos(/212s s ZHRL l A RL l x Y Y πξπ+⋅+= 2） 圆曲线内任意点坐标①由HY ---YH 时⎥⎦⎤⎢⎣⎡++⋅+=R L l A R l R X X s HY πξπ)(90cos )90sin(21 ⎥⎦⎤⎢⎣⎡++⋅+=R L l A R l R Y Y s HY πξπ)(90sin )90sin(21 l ------圆曲线内任意点至HY 点的曲线长； ②由YH---HZ 时⎥⎦⎤⎢⎣⎡+-+⋅+=R L l A R l R X X s H Y πξπ)(90180cos )90sin(22 ⎥⎦⎤⎢⎣⎡+-+⋅+=R L l A R l R Y Y s H Y πξπ)(90180sin )90sin(22 l ------圆曲线内任意点至YH 点的曲线长；3） 第二缓和曲线（HZ---YH ）内任意点坐标)30180cos()30cos(/222ss Z H RL l A RL l x X X πξπ-+⋅+= )30180sin()30cos(/222s s ZH RL l A RL l x Y Y πξπ-+⋅+= l ------第二缓和曲线内任意点至HZ 点的曲线长；。