路线中桩坐标计算

公路施工放线中边桩坐标计算1.确定边坡起点和终点坐标边坡起点是指边坡开始的位置，一般是公路平面路面的外边缘。

边坡终点是指边坡结束的位置，一般是边坡与平面路面的交接点。

边坡起点和终点的坐标可以通过实地测量或根据设计图纸确定。

2.计算边坡的坡度坡度是指边坡的斜率，一般用百分比表示。

计算边坡坡度的方法有以下两种：方法一：直接计算斜率值地面上两点的高差除以两点之间的水平距离，再乘以100，即可得到边坡的坡度。

例如，地面上两点的高差为5米，水平距离为100米，则边坡的坡度为5/100*100=5%。

方法二：利用正切值计算斜率值边坡的坡度可以通过测量边坡的倾斜角度来计算。

根据正切函数的性质，tan(坡度角度)=高差/水平距离。

通过测量边坡起点和终点的高差和水平距离，可以计算出边坡的坡度角度，然后再转化为百分比表示。

3.计算边坡的坡高坡高是指边坡的垂直高度，即边坡起点点位的高程和终点点位的高程之差。

坡高的计算可以直接通过实地测量得到，也可以根据设计图纸上标注的高程数值进行计算。

4.确定边坡的放线点位边坡的放线点位是根据边坡起点和终点的坐标、坡度和坡高进行计算得出的。

根据边坡起点的坐标、坡度和坡高，可以计算出边坡上每个放线点位的坐标和高程。

具体计算方法如下：(1)确定边坡起点的坐标和高程。

(2)根据边坡的坡度和坡高，计算出边坡上每个等分点的高程。

(3)根据边坡起点的坐标和高程，以及等分点的高程，计算出边坡上每个等分点的坐标。

5.检查边坡放线的准确性在计算边坡坐标后，需要进行准确性检查。

可以通过对边坡上的放线点进行测量，然后与计算得出的坐标进行比对，如果两者相差较大，说明计算有误，需要重新计算。

总之，公路施工放线中边坡坐标的计算是一项复杂而重要的任务，需要根据设计要求和实际情况进行准确计算。

通过正确计算边坡的坐标和坡度，可以确保公路施工的质量和安全。

高等级公路中桩边桩坐标计算方法一、平面坐标系间的坐标转换公式如图 9 .设有平面坐标系 xoy 和 x'o'y' （左手系—— x 、 x' 轴正向顺时针旋转90°为 y 、 y' 轴正向）； x 轴与 x' 轴间的夹角为θ（ x 轴正向顺时针旋转至 x' 轴正向.θ范围：0° —360°）。

设 o' 点在 xoy 坐标系中的坐标为（ xo',yo' ）.则任一点 P 在 xoy 坐标系中的坐标（ x,y ）与其在 x'o'y' 坐标系中的坐标（ x',y' ）的关系式为：二、公路中桩边桩统一坐标的计算（一）引言传统的公路中桩测设.常以设计的交点（ JD ）为线路控制.用转点延长法放样直线段.用切线支距法或偏角法放样曲线段；边桩测设则是根据横断面图上左、右边桩距中桩的距离（、）.在实地沿横断面方向进行丈量。

随着高等级公路特别是高速公路建设的兴起.公路施工精度要求的提高以及全站仪、 GPS 等先进仪器的出现.这种传统方法由于存在放样精度低、自动化程度低、现场测设不灵活（出现虚交.处理麻烦）等缺点.已越来越不能满足现代公路建设的需要.遵照《测绘法》的有关规定.大中型建设工程项目的坐标系统应与国家坐标系统一致或与国家坐标系统相联系.故公路工程一般用光电导线或 GPS 测量方法建立线路统一坐标系.根据控制点坐标和中边桩坐标.用“极坐标法”测设出各中边桩。

如何根据设计的线路交点（ JD ）的坐标和曲线元素.计算出各中边桩在统一坐标系中的坐标.是本文要探讨的问题。

（二）中桩坐标计算任何复杂的公路平面线形都是由直线、缓和曲线、圆曲线几个基本线形单元组成的。

一般情况下在线路拐弯时多采用“完整对称曲线”.所谓“完整”指第一缓和曲线和第二缓和曲线的起点（ ZH 或 HZ ）处的半径为∞ ；所谓“对称”指第一缓和曲线长和第二缓和曲线长相等。

线路逐桩坐标计算原理高等级公路、铁路的测设通常要用全站仪应用极坐标法测设中线，利用极坐标法测设中线就必须知道线路中线的点位坐标。

下面就有关计算原理进行说明。

直线段逐桩坐标计算原理直线是线路中最基本的线形。

直线以最短的距离连接两目的地，具有线路短捷，汽车行车方向明确，驾驶操作简单，视距良好等特点，同时直线线形简单也容易计算。

其计算方法和导线类似，知道一个已知点坐标，直线的方位角和距离（即历程差）就能计算未知点里程桩坐标。

如图2-1，例如已知直线A 点坐标和直线方位角AB α以及直线AB 之间的距离AB d 推算B 点坐标：图2-1直线线路⎭⎬⎫+=+=AB AB A B AB AB A B d Y Y d X X ααsin cos （2-1）圆曲线逐桩坐标计算原理铁路与公路线路的平面通常由直线和曲线构成，这是因为在线路的定线中，由于受地形、地物或其他因素限制,需要改变方向。

在改变方向处，相邻两直线间要求用曲线连结起来,以保证行车顺畅安全。

这种曲线称平面曲线。

由于受地形等条件限制，路线总是不断从一个方向转到另一个方向。

这时为了工程能 安全运营，必须用曲线来连接。

其中，圆曲线是最基本线路曲线之一，它是有一定曲率的圆弧。

下面介绍圆曲线的理论计算。

如图2-2所示，直线与圆曲线的连接点称为直圆点（ZY ）；圆曲线的中点称为曲线中点（QZ ）；圆曲线与直线的连接点称为圆直点（YZ ）。

圆曲线要素有线路转向角α，圆曲线半径R ，圆曲线长L ，外矢距E 及切曲差q 。

其中转向角α（单位：度、分、秒）和半径R 是已知数据，其余要素如切线长T ，曲线长L, 外矢距E, 切曲差q 可以按下列关系式计算得出：图2-2圆曲线⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫-=-⨯=⨯=⨯=LT q R E R L R T 2)12(sec1802tanαπαα （2-2） 1)曲线要素计算由交点里程、切线长T 和曲线长L 计算曲线主点里程：ZY 里程 = JD 里程 - 切线长TQZ 里程 = ZH 里程 + L/2YZ 里程 = ZY 里程 + 曲线长L2) ZY 点与YZ 点坐标计算由已知条件和计算出的曲线要素L T 、用极坐标法求出ZY 和YZ 点坐标。

路线中桩坐标的计算公式在道路建设和维护中，桩号是一个非常重要的概念。

它用来表示道路上的位置，帮助工程师和施工人员准确地定位和测量。

桩号通常是以公里为单位，每隔一定距离就会设置一个桩号，以便对道路进行定位和管理。

在本文中，我们将讨论路线中桩坐标的计算公式，以及如何使用这些公式进行实际测量和定位工作。

路线中桩坐标的计算公式通常涉及到道路的曲线和坡度等因素。

在实际测量中，通常会使用全站仪或者GPS等设备来测量各个桩号的坐标，然后根据这些坐标来计算出路线中桩的坐标。

下面我们将介绍几种常见的计算公式。

1. 直线路段的桩坐标计算公式。

在直线路段上，桩号和坐标的计算比较简单。

假设起点的坐标为(x1, y1)，终点的坐标为(x2, y2)，起点的桩号为P1，终点的桩号为P2。

那么在直线路段上任意一个桩号P的坐标可以通过如下公式计算得出：x = x1 + (x2 x1) (P P1) / (P2 P1)。

y = y1 + (y2 y1) (P P1) / (P2 P1)。

其中，x和y分别表示桩号为P时的坐标，P为需要计算坐标的桩号。

2. 曲线路段的桩坐标计算公式。

在曲线路段上，桩坐标的计算会更加复杂一些，需要考虑曲线的半径、圆心、圆心角等因素。

在实际测量中，通常会使用曲线表来进行计算。

曲线表是根据设计参数和曲线类型制定的一张表格，其中包含了各个桩号对应的曲线半径、圆心角等信息。

通过曲线表，可以根据桩号和曲线类型来计算出相应的曲线参数，进而得出桩坐标。

3. 坡度路段的桩坐标计算公式。

在坡度路段上，桩坐标的计算也需要考虑坡度的影响。

假设起点的坐标为(x1,y1)，终点的坐标为(x2, y2)，起点的桩号为P1，终点的桩号为P2，坡度为S。

那么在坡度路段上任意一个桩号P的坐标可以通过如下公式计算得出：x = x1 + (x2 x1) (P P1) / (P2 P1)。

y = y1 + (y2 y1) (P P1) / (P2 P1) + S (P P1)。

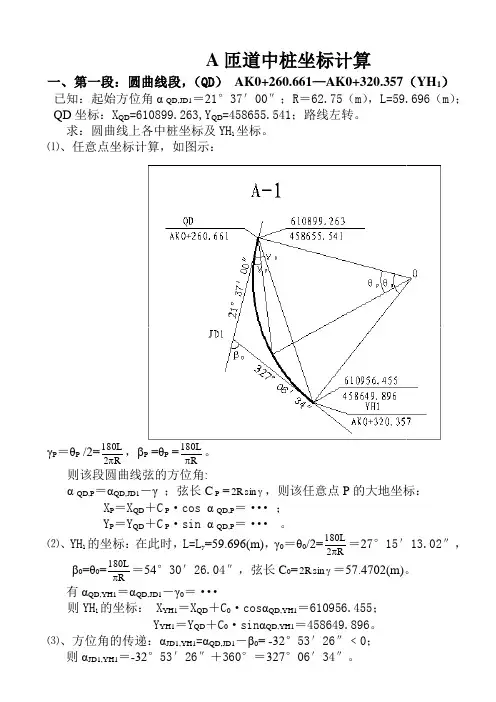
A 匝道中桩坐标计算一、第一段：圆曲线段，（QD ） AK0+260.661—AK0+320.357（YH 1） 已知：起始方位角α QD,JD1＝21°37′00″；R ＝62.75（m ），L=59.696（m ）； QD 坐标：X QD =610899.263,Y QD =458655.541；路线左转。

求：圆曲线上各中桩坐标及YH 1坐标。

⑴、任意点坐标计算，如图示：γP ＝θP /2=R 2L 180π，βP =θP =RL 180π。

则该段圆曲线弦的方位角:α QD,P ＝αQD,JD1－γ ；弦长C P =γsin R 2，则该任意点P 的大地坐标：X P ＝X QD ＋C P ·cos α QD,P ＝··· ；Y P ＝Y QD ＋C P ·sin α QD,P ＝··· 。

⑵、YH 1的坐标：在此时，L=L y =59.696(m)，γ0＝θ0/2=R 2L 180π＝27°15′13.02″，β0=θ0=R L 180π＝54°30′26.04″，弦长C 0=γsin R 2＝57.4702(m)。

有αQD,YH1＝αQD,JD1－γ0＝···则YH 1的坐标： X YH1＝X QD ＋C 0·cos αQD,YH1＝610956.455； Y YH1＝Y QD ＋C 0·sin αQD,YH1＝458649.896。

⑶、方位角的传递：αJD1,YH1=αQD,JD1－β0= -32°53′26″﹤0； 则αJD1,YH1＝-32°53′26″＋360°＝327°06′34″。

二、第二段：缓和曲线段，（YH 1） AK0+320.357—AK0+398.444（HZ 1）已知：起始方位角αYH1,JD2=327°06′34″；R ＝62.75（m ），Ls=59.696（m ）, A=70; YH 1坐标：X YH1=610956.455, Y YH1=458649.896；路线左转。

现阶段我国公路工程中已普遍使用大地坐标进行线型的控制及测设，在施工中经常要对中线坐标进行复核、加密，才能满足公路工程施工的需要。

本文是结合公路工程的实际需要，用于由直线、圆曲线、缓和曲线组成的一般公路线型中桩、边桩等计算的公式。

一、采用公式1 直线段1.1 中桩坐标计算公式1.2 边桩坐标计算公式2 缓和曲线段2.1 中桩坐标计算公式：以ZH点为原点，当曲线左转是Y=(-Y)Xp= X1+X*COSαA→B - Y*SINαA→B，Yp= Y1+X*SINαA→B + Y*COSαA→B以HZ点为原点，当曲线右转是Y=(-Y)Xp= X1-X*COSαB→A + Y*SINαB→A，Yp= Y1-X*SINαB→A - Y*COSαB→A（X=L-L5/40/R2/L s2， Y=L3/6/R/L s）2.2 边桩坐标计算公式：以ZH点为原点以HZ点为原点边桩坐标计算公式：以ZH点为原点坐标中的中桩左侧的“-90°”改为“+90°”，中桩右侧的“+90°”改为“-90°”就OK了。

3 圆曲线段3.1 中桩坐标计算公式当E点位于顺时针方向时取“+”,当E点位于逆时针方向时取“-”。

3.2 边桩坐标计算公式XP、YP——未知点P的坐标X1、Y1——各线型起点的坐标（第二曲线段为终点）XA、YA、XB、YB——P点边桩A点、B点的坐标（A为左侧、B为右侧）α1→2——直线段起点的方位角αA→B——各线形起点的切线方位角（第二曲线段为终点）L——P点距各线形起点的长度LS——缓和曲线段缓和曲线长R——各曲线段的半径β——P点的切线角（曲线左转时取“-”、曲线右转时取“+”）T1、T2——P点至边桩A、B的距离（A为T1、B为T2）边桩与路线切线方向的夹角设定为90°，实际应用中可根据需要进行修改。

中桩坐标的计算一、测量坐标系统（一）大地坐标系统在大地坐标系中，地面点在地球表面上的投影位置用大地经度和大地纬度来表示，地面点的大地坐标是根据大地测量数据由大地坐标原点推算而得，我国大地坐标原点位于陕西泾阳县永乐镇境内，在西安市以北约40Km 处。

（二）高斯3°平面直角坐标系统我国从1952年开始采用高斯投影系统，以高斯投影的方法建立了高斯直角坐标系统。

地面点的高斯平面坐标与大地坐标可以相互转换。

高速公路的勘测设计和施工放样都采用高斯平面直角坐标系统进行的。

（三）平面直角坐标系统在测量范围较小、三级和三级以下公路、独立桥梁隧道及其它构造物，可以把该测区的球面当作平面看待进行直接投影，采用平面直角坐标系统。

二、中桩坐标计算（一）计算导线点的坐标1．方位角的确定：tg β=XY ∆∆ 方位角 : Ai =β （第一象限）Ai =180 °－β （第二象限）Ai =180° + β （第三象限）Ai =360° －β （第四象限）图 2—18 路线的方位角计算2．坐标计算：X i+1 = X i + D CosAiY i+1 = Yi + D SinAi (D ：两导线点间的水平距离)（二）计算中桩坐标１.未设缓和曲线的单圆曲线坐标计算（1）圆曲线起、终点坐标计算JDi 的坐标为（X JDi 、Y JDi ），交点前后直线边的方位角分别为A i -1、A i ，圆曲线的半径为R ，平曲线切线长为T i .,曲线起、终点的坐标可用下式计算：圆曲线起点的坐标： X ZYi = X JDi －T i CosA i -1 Y ZYi = Y JDi －T i SinA i -1圆曲线终点的坐标： X YZi = X Jdi + T i CosA i Y YZi = Y Jdi + T i SinA i图 2—19 中桩坐标计算示意图（2）圆曲线任意点坐标计算ZY ～ QZ 段（YZ ～QZ 段）的坐标计算以曲线起点ZY （曲线终点YZ 点）为坐标原点，切线为X ′轴，法线为Y ′轴，建立直角坐标系:X ′= R Sin(π180'R l ) Y ′= R －R Cos (π180'R l ) 式中： l ′———圆曲线上任意点至 ZY （YZ ）点的弧长；ZY ～QZ 段的各点的坐标：利用上述公式计算出以ZY 为坐标原点圆曲线段内各加桩X ′、Y ′ 的值，则ZY ～QZ 段的各点的坐标和方位角为：X = X ZYi - X ′ CosA i -1 – ζY ′sin A i -1Y = Y ZYi + X ′ SinA i -1 +ζY ′cos A i -1YZ ～QZ 段的各点的坐标：利用上述公式计算出以YZ 为坐标原点圆曲线段内各加桩X ′、Y ′ 的值，则ZY ～QZ 段的各点的坐标为：X= X YZi - X ′ CosA i –ζY ′Sin A iY= Y YZi - X ′ SinA i +ζY ′Cos A i式中：ζ — 路线转向，右转角时ζ=1，左转角时ζ= -1，以下各式同。

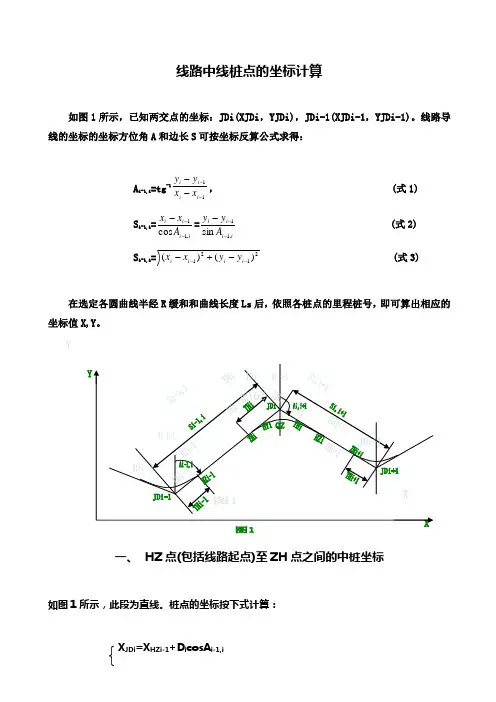
线路中线桩点的坐标计算如图1所示，已知两交点的坐标：JDi(XJDi ，YJDi)，JDi-1(XJDi-1，YJDi-1)。

线路导线的坐标的坐标方位角A 和边长S 可按坐标反算公式求得：A i-1,i =tg -111----i i i i x x y y ， (式1)S i-1,i =i i i i A x x ,11cos ---=ii i i A y y ,11sin --- (式2)S i-1,i =2121)()(---+-i i i i y y x x (式3)在选定各圆曲线半经R 缓和和曲线长度Ls 后，依照各桩点的里程桩号，即可算出相应的坐标值X,Y 。

一、 HZ 点(包括线路起点)至ZH 点之间的中桩坐标如图1所示，此段为直线。

桩点的坐标按下式计算：X JDi =X HZi-1+D i cosA i-1,iY JDi =Y HZi-1+D i sinA i-1,I (式4)式中A i-1,i 为线路导线JDi-1到JDi 的坐标方位角；Di 为桩点到HZi-1的距离(Si-1,i –THi-1)，即桩点里程与HZi-1点里程之差；X HZi-1、Y HZi-1为HZi-1点的坐标，由下式计算：XHZi-1=X JDi-1+T Hi-1cosA i-1,iY HZi-1=X JDi-1+T Hi-1sinA i-1,i (式5) 同理计算出直线终点ZHi 点的坐标 X ZHi =X JDi-1+(Si-1,i –THi)cosA i-1,iY ZHi =X JDi-1+(Si-1,i –THi)sinA i-1-I (式6)二、 ZH 点至YH 点之间的中桩坐标如图1所示,此段包括第一缓和曲线及圆曲线,先计算桩点的切线支距法坐标x 、y ：1、缓和曲线上桩点的切线支距法坐标x 、y ：X=()L -22540SL R L Y=SRL L 63(式7)L 为桩点(测点)到缓和曲线起点ZH 的曲线长，即测长；R 为圆曲线半径；L S 为缓和曲线总长2、圆曲线上桩点的切线支距法坐标x 、y ：以ZH 为起点：(带有缓和曲线的圆曲线，)X=Rsin ϕ+q=Rsin )2(1800S L L R +π+2S L –23240RL SY=R(1－cos ϕ)+p=R 〔1–cos )2(1800S L L R +π〕+RL S 242 (式8) ○1L 为桩点到HY(缓圆点,既圆曲线的起点)的曲线长，仅为圆曲线部份的长度，那么：式中ϕ=α+βo =RL π180⨯+βo =R L π0180⨯+πR L S 21800⨯=)2(1800S L L R +π， ○2假设L 为桩点到ZH(直缓点)的曲线长，那么：式中ϕ=α-βo =RL π180⨯-βo =R L π0180⨯-πR L S 21800⨯=)2(1800S L L R -π。

路线逐桩坐标计算高等级公路路线设计中，必须计算各点位的逐桩坐标，以作为路线施工放样的依据，也是公路交工和峻工验收时检测中线偏位的依据，故坐标计算能力，已是道路桥梁工程技术专业学生的必备技能。

1、路线交点偏角、交点间距、曲线要素及主点桩计算如图所示，设路线起点坐标JD0(XJ0,YJ0), 任一交点i的坐标为JD i(XJ i,YJ i),i =1,2,3, .n,贝肪目邻两交点之间的AX iJM =XJD j - XJD j」坐标增量：£ 丄=YJD -YJD」路线交点坐标计算：X JD=X JDL+AX j丄YJD=YJDj+AY』i交点间距：S i C ：X i J,i ）' （”Y i」,i）象限角耳出=arctan------------ -A x-象限角与方位角A之间关系0,时，耳斗位于第一象限， A -J,iX i J 「：：OCYj,i•0,时，耳屮位于第二象限， A 4, i = 180 i4,iX i, 「：：0,弓沖以0,时,位于第三象限，A i 4i = 180 jX i, 「OU ：：:0,时,q_u位于第四象限，A斗i =360—= i斗,“ ...A f“I .rH■- "J ¥arL...X路线偏角i等于后方位角减前方位角：〉=二2 -片般情况下，:-i为正时，曲线右偏；:-i为负时，曲线左偏。

2、直线段上中桩坐标计算图中，设交点i的坐标为Jdi（Xji,YJi），交点i前后相邻直线的方位角分别为A/,i和A i,i+i. 贝UX ZHi =XJD j +壬8$律_|」+180)ZH（或ZY）点的坐标：Y zHi =YJD i +T i S in (A」i +180)HZ（或YZ）点的坐标：XHZi= XJDiTi COSA,i 1 YHZi =YJD +工sin A,r设直线上加桩里程为L , ZHi、Hzi表示曲线i的起、终点里程，则交点i前直线上任意点坐标（L空ZH i ）。

高等级公路中桩边桩坐标计算方法一、平面坐标系间的坐标转换公式如图9 ，设有平面坐标系xoy 和x'o'y' （左手系—— x 、x' 轴正向顺时针旋转90°为y 、y' 轴正向）；x 轴与x' 轴间的夹角为θ（x 轴正向顺时针旋转至x' 轴正向，θ范围：0°— 360°）。

设o' 点在xoy 坐标系中的坐标为（xo',yo' ），则任一点P 在xoy 坐标系中的坐标（x,y ）与其在x'o'y' 坐标系中的坐标（x',y' ）的关系式为：二、公路中桩边桩统一坐标的计算（一）引言传统的公路中桩测设，常以设计的交点（JD ）为线路控制，用转点延长法放样直线段，用切线支距法或偏角法放样曲线段；边桩测设则是根据横断面图上左、右边桩距中桩的距离（、），在实地沿横断面方向进行丈量。

随着高等级公路特别是高速公路建设的兴起，公路施工精度要求的提高以及全站仪、GPS 等先进仪器的出现，这种传统方法由于存在放样精度低、自动化程度低、现场测设不灵活（出现虚交，处理麻烦）等缺点，已越来越不能满足现代公路建设的需要，遵照《测绘法》的有关规定，大中型建设工程项目的坐标系统应与国家坐标系统一致或与国家坐标系统相联系，故公路工程一般用光电导线或GPS 测量方法建立线路统一坐标系，根据控制点坐标和中边桩坐标，用“极坐标法”测设出各中边桩。

如何根据设计的线路交点（JD ）的坐标和曲线元素，计算出各中边桩在统一坐标系中的坐标，是本文要探讨的问题。

（二）中桩坐标计算任何复杂的公路平面线形都是由直线、缓和曲线、圆曲线几个基本线形单元组成的。

一般情况下在线路拐弯时多采用“完整对称曲线”，所谓“完整”指第一缓和曲线和第二缓和曲线的起点（ZH 或HZ ）处的半径为∞ ；所谓“对称”指第一缓和曲线长和第二缓和曲线长相等。