下载文档原格式
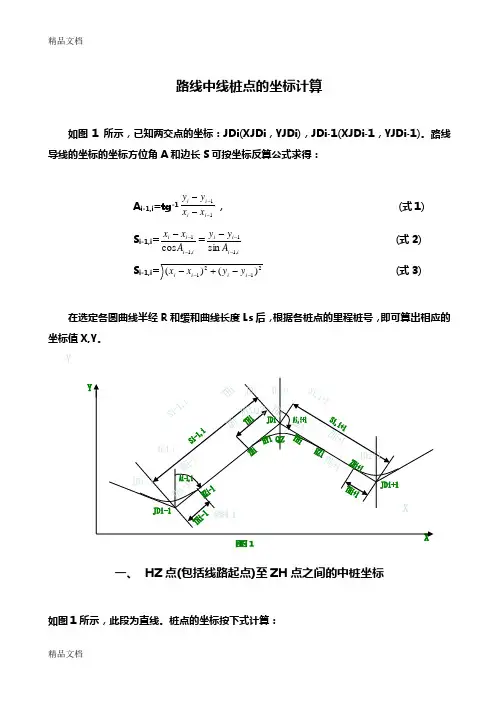
路线逐桩坐标计算高等级公路路线设计中，必须计算各点位的逐桩坐标，以作为路线施工放样的依据，也是公路交工和峻工验收时检测中线偏位的依据，故坐标计算能力，已是道路桥梁工程技术专业学生的必备技能。
1、 路线交点偏角、交点间距、曲线要素及主点桩计算如图所示，设路线起点坐标),,(000YJ XJ JD 任一交点i 的坐标为,,...3,2,1),,(n i YJ XJ JD i i i =则相邻两交点之间的坐标增量：1,11,1-----=∆-=∆i i i i i i i i YJD YJD Y XJD XJD X路线交点坐标计算：ii i i i i i i Y Y J D Y J D X X J D X J D ,11,11----∆+=∆+=交点间距：2,12,1,1)()(i i i i i i Y X S ---∆+∆=象限角i,1i i ,1i ,1X Y arctan---∆∆=i i θ象限角与方位角A 之间关系i i i i i i i i i i A Y X ,1,1,1,1,1,0,0-----=>∆>∆θθ位于第一象限，时，i i i i i i i i i i A Y X ,1,1,1,1,1180,0,0-----=>∆<∆θθ－位于第二象限，时， i i i i i i i i i i A Y X ,1,1,1,1,1180,0,0-----+=<∆<∆θθ 位于第三象限，时， i i i i i i i i i i A Y X ,1,1,1,1,1360,0,0-----=<∆>∆θθ－位于第四象限，时，路线偏角i α 等于后方位角减前方位角： 12θθα-=一般情况下，i α为正时，曲线右偏；i α为负时，曲线左偏。
2、 直线段上中桩坐标计算图中，设交点i 的坐标为Jdi(Xji,YJi)，交点i 前后相邻直线的方位角分别为A i-1,i 和A i,i+1.则ZH(或ZY)点的坐标: )180sin()180cos(,1,1++=++=--i i i i ZHi i i i i ZHi A T YJD Y A T XJD XHZ(或YZ)点的坐标:1,1,sin cos +++=+=i i i i HZi i i i i HZi A T YJD Y A T XJD X设直线上加桩里程为L ，ZHi 、Hzi 表示曲线i 的起、终点里程，则交点i 前直线上任意点坐标（i ZH L ≤）。
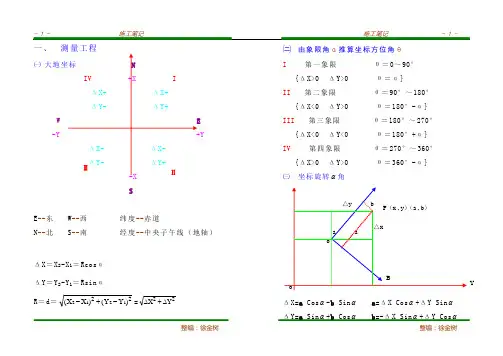
一、㈠ 大地W -Y SE --东 W --西 纬度--赤道N --北 S --南 经度--中央子午线（地轴）ΔX ＝X 2-X 1＝Rcos α ΔY ＝Y 2-Y 1＝Rsin αR ＝d ＝22)()(1212Y -Y +X -X =22∆Y +∆X㈡ 由象限角α推算坐标方位角θI 第一象限 θ＝0～90°{ΔX>0 ΔY>0 θ＝α}II 第二象限 θ＝90°～180°{ΔX<0 ΔY>0 θ＝180°-α} III 第三象限 θ＝180°～270°{ΔX<0 ΔY<0 θ＝180°+α} IV 第四象限 θ＝270°～360°{ΔX>0 ΔY>0 θ＝360°-α} ㈢ 坐标旋转α角 ΔX=a Cos α-b Sin α a =ΔX Cos α+ΔY Sin α ΔY=a Sin α+b Cos α b =-ΔX Sin α+ΔY Cos α㈣ 极坐标M （Ρ.θ）与直角坐标变换 X ＝ΡSin θ Y ＝ΡCos θΡ²＝X ²+Y ²tg θ＝YX㈤ 测绘公式★经纬仪测距远离及公式D ＝ct D--平距 t--读数 c--100 D ＝c ·Cos δ·t δ---竖直角 h ＝21c ·t ·Sin2δ h---高差 ★光电测距仪的测量原理D ＝21·c ·t t--时间 c--光速c ＝2997925 km/秒 ★ 等高线插分d x ＝hd ∆·h x d---图纸平距 Δh---高程差Δh ＝h 2-h 1 h x ---分部高程★全站仪测量高程改正值ff ＝0.43·RD 2R―地球半径 R ＝6371km D---两点间距离已知导线点D 5（X 5,Y 5）为测站点，D 4（X 4,Y 4）为后 视点； Kn ＋100（X 1,Y 1）α54=tg-1（5454X X Y Y --） α51=tg -1（5151X X Y Y --）β1=α51－α54 S 1=（（X 5-X 1）2＋（Y 5-Y 1）2）㈦园曲线、缓圆曲线要素★要素名称ZY---曲线起点（直圆点）QZ---曲线中点YZ---曲线终点（圆直点）JD--转角点即两切线交点α---外偏角，即路线转向角αz(左) αy（右）R---圆曲线半径L---曲线全长T---切线长，即从转向角点至曲线终点的距离c---曲线弦长h---弓形高E---曲线外矢距，即JD至QZ的距离D---整弧（一般为20m或50m）所对中心角α---分弧（小于整弧数）所对中心角ZH---曲线起点（直圆点）HZ---曲线终点（缓直点）HY---缓圆点YH---圆缓点C---缓和曲线弦长L---缓和曲线长度m---自曲线起点或曲线终点垂直线终点的距离p---圆曲线自切线向内移动的距离ß---缓和曲线中心角x---缓和曲线与圆曲线连接点的横距y---缓和曲线与圆曲线连接点的纵距δ-曲线起点共和国共和国或曲线终点HZ至HY或YH偏角值N²δ---曲线起点至缓和曲线任意点的偏角值A---缓和曲线参数 Q---公切点（GQ）q---地曲差（矫正值或J、Dn）★缓和曲线公式ß＝R l 20 ρ＝R l 20·π180＝l R l .22·π180＝28.6479Rl(°) δ＝3β＝R l 6 x 0＝L ―2340R l y 0＝R l 62―34336R lm ＝x 0―R ·S inß＝2l ＝2l―23240R l p ＝y 0―R ·v ersß＝y 0―R(1-C osß)＝R l 242―342688R l＝51.0416·R1―558.268·31R ＝R l 62T ＝(R+p)tg 2a+mE ＝(R+p)exsec 2a +p ＝(R+p)Sec 2a―Rsec 2a＝21a CosL ―2L 0＝(α-2ß)ρR ＝ 180π·R(α-2ß)C 0＝2020Y +X ＝x 0·sec δ＝L 0―23090Rlq ＝2T-LA ＝0L R •3R≤A ≤R 100m ≤R ≤300m m ＝x 0―Rsinß ß＝π90·Rlx 0＝L 0―23040R LC 0＝x 0·sec δT ＝x 0―y 0ctg ß y 0＝RL 620―34336R L p ＝y 0―R(1-cosß)★圆曲线公式 T ＝R tg2a L ＝ 180..R a π L ＝”.ρRa ρ″＝206264″.81 ”3600180π⨯＝206264″.81E ＝R exsec2a ＝R(sec 2a―1)＝2a Cos R ―RSec2a =21aCos C ＝2R Sin 2aq ＝2T ―LD ＝R LP ρ″ (L p ＝20m 或50m)d i=R li ρ″ （｜i ＜｜p ）2R ＝h+h C 42 h ＝R C 82＝R(1―Cos 2a)★ 偏角法2a ＝RBA -·πο90＝(A ―B) ·R π 90弦长＝2R ·Sin R L 2·π180 (2a---弦切角 A---前桩号 B---后桩号、ZY 或YZ)★缓和曲线支距法X ＝L x ―202540L R L X ßx＝0290RL L XπY ＝036RL LX ―337336X X L R L θx ＝θ+ ßx★曲线部分 X ＝Rsin(α′+ß)+m Y ＝R{1―cos(α′+ß)}+pX---缓和曲线（或主曲线）上任一点的横距 Y---缓和曲线（或主曲线）上任一点的纵距L x ---缓和曲线起点至缓和曲线上任一点的曲线长α′缓和曲线终点至主曲线上任一点曲线相对应的中心角㈧ 坐标、水准计算闭合方位角闭合f B ＝ f x ＝ f y ＝ f B 允＝10n 坐标相对闭合差＝Dy f x f 22..+导线复测，角度闭合差（″）为±n 16 n 是测点数 坐标相对闭合差为±100001横断面每20m 一段，填挖分清水准闭合差△h 应达到 f 允 ≤±20L ㎜ ≤±4n ㎜ 或 ≤±61+n ㎜L---为水准路线长度，以km 计 n —为测站数（单程）㈨ 计算曲线要素、元素和主点里程内移值 P ＝R Ls 242 切线角 ß0＝R Ls 2·π︒180切线增长值 q ＝2Ls―23240R Ls Ls 缓和曲线长度缓和曲线终点的直角坐标：X h ＝L s ―2340R Ls 切线长 T h＝(R+p)·tg(2a)+q Y h ＝R Ls 62 圆曲线长 L y ＝R(α-2ß)︒180π切曲差D h ＝2T h ―L h 曲线长L y ＝(α-2ß)︒180.Rπ +2L S交点 JD 里程 直缓点里程）⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯-ZH Th缓圆点里程）⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯+HY Ls圆缓点里程）⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯+YH Ly缓直点里程）⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯+HZ Ls曲中点里程）⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯-QZ Lh2 交点里程）⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯+JD Dh2 （校核）㈩坐标推导（理论）已知：两点的坐C 标分别为A（Xa,Ya），B（Xb,Yb）b a 求：点C的坐标C（Xc,Yc）A cB 解：算出A、B两点的坐标差，△X=Xb-Xa，△Y=Yb-Yac=（△X2＋△Y2），再利用两点坐标公式（或程序）求出A→B的方位角θa和B→A的方位角θb，再利用正弦定理公式Aasin=Bbsin=Ccsin实测：①♀A→B 得θab ♀A→C 得θac 算出内角A②♀B→A 得θba ♀B→C 得θbc 算出内角B③内角C=180-A-B，同时算出边a和b的值④根据♀A→C中b值和θac值求出△X1和△Y1，可求出点C的坐标（Xc1,Yc1）⑤根据♀B→C中a值和θbc值求出△X2和△Y2可求出点C的坐标（Xc2,Yc2）⑥比较Xc1,Yc1和Xc2,Yc2最终求出点C正确的坐标﹙＋－﹚三角函数关系式：Cb aαA c D BSinα＝catgα＝baSecα＝acCosα＝cbctgα＝abCoseα＝bctgα＝aCosaSin..ctgα＝aSinaCos..c²＝a²+b²ASina.＝BSinb.＝CSinc.＝2Ra²＝b²+c²-2bc CosA a＝b CosC+c CosBb²＝a²+c²-2ac CosB b＝c CosA+a CosCc²＝a²+b²-2ab CosC c＝a CosB+b CosASin a·Cos a=1 Sin a·Sec a=1Cos a·Cose a=1 tg a·ctg a=1Sin2a+Cos2a=1 Sec2a+tg2a=1Cose2a+ctg2a=1﹙＋二﹚两点间距离 X ＝λλ++121X X Y ＝λλ++121Y Y斜率k ＝tg α＝1212X X Y Y --＝-BA定比分点λ＝21..P P P PAX+BY+C ＝0 Y ＝Kx+bY-Y 1＝k （X-X 1） 121Y Y Y Y --＝121X X X X --两条直线所成角α（θ为方位角） tg α＝1212..θθθθtg tg H tg tg -＝｜2112.1K K K K +-｜点到直线距离 d ＝2200BA CBY AX +++交点坐标： X ＝12211221....B A B A C B C B -- Y ＝12211221....B A B A A C A C --（十二）二次方程：ax ²+bx+c ＝0x ＝aac b b 242-±- (△=b ²-4ac ≥0)（十三）变更时曲线测设计算R —新曲线半径 R ′—旧曲线半径α.（α′）—新（旧）切线转角（外角） e —变更距离 、m 、n —新旧切线间的距离 1.在旧曲线中央变动一定距离 R ＝R ′-12sec-αe （两切点相应变动）2.移动旧曲线使与平行于旧切线的新切线连接 m=n ＝α.sin e＝m.cos α＝e.ctg α 3.变动旧曲线与新切线连接（起点不动）R ＝R ′－α.cos 1－e n ＝e.ctg 2α4. 变动旧曲线与新切线连接（终点不向前进） R ＝R ′－1.sec －αen ＝（R ′－R ）tg α5.在曲线起点（或终点）变更切线方向改设曲线 R ＝ααcos 1)'.cos 1.'－－（R n ＝R.sin α－R ′.sin α′6.在交点处（P ）变更切线方向 R ＝R ′tg 2.'α.ctg2α7.依既定切线位置使曲线通过一定点—交点P 到定点Q 的距离β—PQ 与PO 夾角 γ—OQ 与OP 夾角 α′—为∠PQO θ—为切线与定点的外角 Sin α′＝2cos2αθα）＋（ β＝90°－2α－θγ＝180°－α′－β R ＝γβ.sin .sin .二、求积公式：1、棱台公式计算： V ＝31D(A 1+A 2+21A ⨯A ) V ＝21D(A 1+A 2) A 1 A 2为两断面面积，D 为间距 2、球体体积： V 球＝3∆πR ³3、不规则多边形积 ★梯形积分法：A=（211++n L L +∑=ni 2·L i ）·h=h ·∑=ni 1·L中iL中i是（i=1、2……h ）定每个梯形中位线长度★方格网法：总格数=完整格数+21（不完整格数） 图形积=每小格的面积×总格数三、强夯技术参数： E=Gh H=k h G .E---夯能（500～3000KJ/m 2） G---夯锤重（t ） k---系数、一般0.4～0.7 h---落距（m ） H----加固影响深度（m ）四、锚杆锚固：Le ≥］d ［Nek τπ.1=KD Ne k τπ...2 Le--有效锚杆长度（㎝）Ne--锚杆承受的拉力（KN ） K2--安全系数.取2～3 ［τ］--砂浆与锚杆之间的抗剪强度或砂浆与岩石之间的抗剪强度（N/cm 2） d--锚杆直径（cm ） K 1—安全系数.取 1.5～2.0 D--锚孔直径（cm ）τk ---锚固段砂浆与土层接触面间的抗剪强度或孔壁土层的抗剪强度、取两者间较小值（N/cm 2） 板桩配锚支撑法，钢筋砼板墙厚20㎝五、单位数据 钢材材积计算公式1、无缝钢管：每米重量＝外径－壁厚×壁厚×0.02466 2、钢管：每米重量＝0.02466×壁厚（外壁－壁厚） 3、钢板、扁钢、钢带： 每米重量＝0.00785×寛×厚4、方钢：每米重量＝0.00785×边长×边长 5、圆钢、线材、钢丝： 每米重量＝0.00617×直径×直径 6、六角钢：每米重量＝0.0068×对边距离×对边距离 7、八角钢：每米重量＝0.0065×对边距离×对边距离 8、等边角钢：每米重量＝0.00785×边厚（2边寛－边厚） 9、不等边角钢：每米重量＝0.00785×边厚（长边寛＋短边寛－边厚） 每米重量＝0.00785×[短边寛（长边寛＋短边寛－边厚）＋0.215(内弧半径×内弧半径－2端弧半径×端弧半径) ]10、工字钢：每米重量＝0.00785×[高＋f（腿寛－腰寛）]每米重量＝0.00785×[高×腰厚＋2平均腿厚（腿长－腰厚）＋0.615（内弧半径×内弧半径－端弧半径×端弧半径) ] 11、槽钢：每米重量＝0.00785×[高＋e（腿寛－腰寛）]每米重量＝0.00785×[高×腰厚＋2平均腿厚（腿长－腰厚）＋0.349（内弧半径×内弧半径－端弧半径×端弧半径) ]附注：①角钢、工字钢和槽钢的准确计算公式很繁，表列简式用于计算近似值。
公路逐桩坐标计算程序(可以计算对称、不对称缓和曲线)Lb1 0Z=？V=？W=V+2：Fixm｛K｝Lb1 1K>Z[W+5Z+4]=>W=W+1:Goto 1⊿(判断桩号在哪个交点范围，就是该交点曲线起点至下一交点曲线起点) S=K-Z[W+5Z+3] （计算该桩号与曲线起点的距离）R=Z[W+2Z+2]：L=Z[W+3Z+2]:E=Z[W+4Z+2] （读取该交点曲线要素R、Ls1 、Ls2）Pol（Z[W]-Z[W-1],Z[W+Z+2]-Z[W+Z+1]）（计算该交点与下一交点直线方位角）J<0=>J=J+360⊿A=JPol（Z[W-1]-Z[W-2],Z[W+Z+1]-Z[W+Z]）（计算该交点与上一交点直线方位角）J<0=>J=J+360⊿C=A-J:A=J （计算偏角）W=V+2=>Goto2⊿（如果桩号在起点与第一交点曲线起点之间，则转Lb1 2 ）I=Abs（tan（c÷2））M=L÷2-L^3÷240R^2:N=E÷2-E^3÷240R^2P=L^2÷6R-L^4÷336R^3-R（1-cos（90L÷πR））Q=E^2÷6R-E^4÷336R^3-R（1-cos（90E÷πR））D=（P-Q）I÷2 : F=（P+Q+2R）I÷2M=F+M-D:Q=F+N+DN=πRAbsC÷180+（L+E）÷2X=Z[W-1]-McosAY=Z[W+Z+1]-MsinAM=Z[W-1]+Qcos（A+C）V=Z[W+Z+1]+Qsin（A+C）Q=AbsC÷CS≤L=>P=0:Goto3⊿（如果桩号在第一缓和曲线内，则转Lb1 3）S≤N-E=>S=S-L:Goto4⊿（如果桩号在圆曲线内，则转Lb1 4）S≤N=>S=N-SQ=-Q:A=A+C-180:X=M:Y=V:L=E：P=180:Goto3 ⊿（如果桩号在第二缓和曲线内，则转Lb1 3）P=A+C:S=S-N:D=M+ScosP:F=V+SsinPGoto6 （如果桩号在直线内，则转Lb1 6）Lb1 2P=A+CD=Z[W-1]+ScosPF=Z[W+Z+1]+SsinP:Goto6Lb1 3I=S-S^5÷40R^2÷L^2+S^9÷3456R^4÷L^4J=Q（S^3÷6RL-S^7÷336R^3÷L^3）P=P+A+90Q S^2÷πRL:Goto5Lb1 4M=90（2S+L）÷πRI=RsinM+L÷2-L^3÷240R^2J=Q（L^2÷24R+R（1-cosM））P=A+QMLb1 5D=X+IcosA-jsinA:F=Y+JcosA+IsinALb1 6D″X=″◢（结果显示X坐标）F″Y=″◢（结果显示Y坐标）P″AT=″◢（结果显示该桩号方位角）{BO}：B″S″O″⊿″ （输入边桩距离，交角）P=P+OL″XB″=D+BcosP◢（结果显示边桩X坐标）M″YB″=F+Bs inP◢（结果显示边桩Y坐标）以上是坐标计算程序，括号内是程序计算的大致原理及说明，中间部分为直线、圆曲线、缓和曲线计算的各种公式，大家也知道，书上也有。
公路施工放线中边桩坐标计算1.确定边坡起点和终点坐标边坡起点是指边坡开始的位置，一般是公路平面路面的外边缘。
边坡终点是指边坡结束的位置，一般是边坡与平面路面的交接点。
边坡起点和终点的坐标可以通过实地测量或根据设计图纸确定。
2.计算边坡的坡度坡度是指边坡的斜率，一般用百分比表示。
计算边坡坡度的方法有以下两种：方法一：直接计算斜率值地面上两点的高差除以两点之间的水平距离，再乘以100，即可得到边坡的坡度。
例如，地面上两点的高差为5米，水平距离为100米，则边坡的坡度为5/100*100=5%。
方法二：利用正切值计算斜率值边坡的坡度可以通过测量边坡的倾斜角度来计算。
根据正切函数的性质，tan(坡度角度)=高差/水平距离。
通过测量边坡起点和终点的高差和水平距离，可以计算出边坡的坡度角度，然后再转化为百分比表示。
3.计算边坡的坡高坡高是指边坡的垂直高度，即边坡起点点位的高程和终点点位的高程之差。
坡高的计算可以直接通过实地测量得到，也可以根据设计图纸上标注的高程数值进行计算。
4.确定边坡的放线点位边坡的放线点位是根据边坡起点和终点的坐标、坡度和坡高进行计算得出的。
根据边坡起点的坐标、坡度和坡高，可以计算出边坡上每个放线点位的坐标和高程。
具体计算方法如下：(1)确定边坡起点的坐标和高程。
(2)根据边坡的坡度和坡高，计算出边坡上每个等分点的高程。
(3)根据边坡起点的坐标和高程，以及等分点的高程，计算出边坡上每个等分点的坐标。
5.检查边坡放线的准确性在计算边坡坐标后，需要进行准确性检查。
可以通过对边坡上的放线点进行测量，然后与计算得出的坐标进行比对，如果两者相差较大，说明计算有误，需要重新计算。
总之，公路施工放线中边坡坐标的计算是一项复杂而重要的任务，需要根据设计要求和实际情况进行准确计算。
通过正确计算边坡的坐标和坡度，可以确保公路施工的质量和安全。
高等级公路中桩边桩坐标计算方法一、平面坐标系间的坐标转换公式如图 9 .设有平面坐标系 xoy 和 x'o'y' （左手系—— x 、 x' 轴正向顺时针旋转90°为 y 、 y' 轴正向）； x 轴与 x' 轴间的夹角为θ（ x 轴正向顺时针旋转至 x' 轴正向.θ范围：0° —360°）。
设 o' 点在 xoy 坐标系中的坐标为（ xo',yo' ）.则任一点 P 在 xoy 坐标系中的坐标（ x,y ）与其在 x'o'y' 坐标系中的坐标（ x',y' ）的关系式为：二、公路中桩边桩统一坐标的计算（一）引言传统的公路中桩测设.常以设计的交点（ JD ）为线路控制.用转点延长法放样直线段.用切线支距法或偏角法放样曲线段；边桩测设则是根据横断面图上左、右边桩距中桩的距离（、）.在实地沿横断面方向进行丈量。
随着高等级公路特别是高速公路建设的兴起.公路施工精度要求的提高以及全站仪、 GPS 等先进仪器的出现.这种传统方法由于存在放样精度低、自动化程度低、现场测设不灵活（出现虚交.处理麻烦）等缺点.已越来越不能满足现代公路建设的需要.遵照《测绘法》的有关规定.大中型建设工程项目的坐标系统应与国家坐标系统一致或与国家坐标系统相联系.故公路工程一般用光电导线或 GPS 测量方法建立线路统一坐标系.根据控制点坐标和中边桩坐标.用“极坐标法”测设出各中边桩。
如何根据设计的线路交点（ JD ）的坐标和曲线元素.计算出各中边桩在统一坐标系中的坐标.是本文要探讨的问题。
（二）中桩坐标计算任何复杂的公路平面线形都是由直线、缓和曲线、圆曲线几个基本线形单元组成的。
一般情况下在线路拐弯时多采用“完整对称曲线”.所谓“完整”指第一缓和曲线和第二缓和曲线的起点（ ZH 或 HZ ）处的半径为∞ ；所谓“对称”指第一缓和曲线长和第二缓和曲线长相等。
