材料力学第二版范钦珊高教版答案 第八章
- 格式:doc
- 大小:145.00 KB
- 文档页数:3


材料力学习题集第1章引论1-1图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M。
关于固定端处横截面A -A上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
A-A在(b-1)(a-1) (b-1)(a-2) (b-2)(c) (d)(c-2) (d-2)(e) (f)(e-1) (f-1)(e-2) (a) (b)(c) (d)(a-1)(c-1) (d-1)(f-2)(b )0=∑A M ,022R 2=⋅+⋅+⋅--l F l ql lql ql B , ql F B 41R =(↑) 0=∑y F ,ql F A 41R =(↓), 2R 4141ql l ql l F M B C =⋅=⋅=(+) 2ql M A =(c )0=∑y F ,ql F A =R (↑) 0=∑A M ,2ql M A =0=∑D M ,022=-⋅-⋅+D M lql l ql ql(d )0=∑B Mql F A 45R =(↑) 0=∑y F ,ql F B 43R =(↑)0=∑B M ,22l qM B =0=∑D M ,23225ql M D = (e )0=∑y F ,F R C = 00=∑C M ,0223=+⋅+⋅-C M lql l ql0=∑B M ,221ql M B =0=∑y F ,ql F B =Q2max ||ql M =(f )0=∑A M ,ql F B 21R =(↑)0=∑y F ,ql F A 21R =(↓)0=∑y F ,021Q =-+-B F ql ql0=∑D M ,042221=+⋅-⋅D M ll q l ql281ql M E =∴ ql F 21||max Q =2-5 试作图示刚架的弯矩图,并确定max ||M 。
解: 图(a ):0=∑A M ,02P P R =⋅-⋅-⋅l F l F l F B P R F F B =(↑)0=∑y F ,P F F Ay =(↓) 0=∑x F ,P F F Ax =(←)弯距图如图(a-1),其中l F M P max 2||=,位于刚节点C 截面。


第一章绪论一、选择题1.根据均匀性假设,可认为构件的(C)在各处相同。
A.应力B.应变C.材料的弹性系数D.位移2.构件的强度是指(C),刚度是指(A),稳定性是指(B)。
A.在外力作用下构件抵抗变形的能力B.在外力作用下构件保持原有平衡状态的能力C.在外力作用下构件抵抗强度破坏的能力3.单元体变形后的形状如下图虚线所示,则A点剪应变依次为图(a) (A),图(b) (C),图(c) (B)。
A.0B.r2C.r D.1.5r4.下列结论中( C )是正确的。
A.内力是应力的代数和;B.应力是内力的平均值;C.应力是内力的集度;D.内力必大于应力;5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力,它们的应力是否相等(B)。
A.不相等;B.相等;C.不能确定;6.为把变形固体抽象为力学模型,材料力学课程对变形固体作出一些假设,其中均匀性假设是指(C)。
A. 认为组成固体的物质不留空隙地充满了固体的体积;B. 认为沿任何方向固体的力学性能都是相同的;C. 认为在固体内到处都有相同的力学性能;D. 认为固体内到处的应力都是相同的。
二、填空题1.材料力学对变形固体的基本假设是连续性假设,均匀性假设,各向同性假设。
2.材料力学的任务是满足强度,刚度,稳定性的要求下,为设计经济安全的构件提供必要的理论基础和计算方法。
3.外力按其作用的方式可以分为 表面力 和 体积力 ,按载荷随时间的变化情况可以分为 静载荷 和 动载荷 。
4.度量一点处变形程度的两个基本量是 (正)应变ε 和 切应变γ。
三、判断题1.因为构件是变形固体,在研究构件平衡时,应按变形后的尺寸进行计算。
( × ) 2.外力就是构件所承受的载荷。
( × ) 3.用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
( √ ) 4.应力是横截面上的平均内力。
( × ) 5.杆件的基本变形只是拉(压)、剪、扭和弯四种,如果还有另一种变形,必定是这四种变形的某种组合。
比较:图(a-1)与图(b-1)不同,因两者之1 - 3试画出图示各物体的受力图。
1 - 1图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方 F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
解:(a),图(c ):分力: 投影:=90 ° 时, (d ): F cos i 1 FX 1F y1 F sin F y1 F sinj l讨论:(b ),图F X 1 F cos投影与分力的模相等;分力是矢量, X 2投影是代数量。
F sinsin分力: j2BD(b)D(b-1)(a-3)投影: 工90°时, F X 2 F cos , 投影与分量的模不等。
讨论:1 -2试画出图a 、b 两情形下各物体的受力图,并进行比较。
F y2 F cos(F X 2 (F cos F sin tan )i 2 F y2(a)l F AyF A X1F RD 值大小也不同。
a5A■dFBFF CABB(a-1)(b-1)BC DBCBCWDAy或(b-2)(c-1)(d-1)DCABCDFt D或(d-2)(e-2)(e-1)CO iOyBFA(f-3)(e-3)IV2[fW(f-1)(c)习题1—3图F BF BF AxF AF DB FF cW(f-2)AOAF A力 F i 作用在,并加以讨论。
----------------- :B 铰上。
杆AB 不计自重,杆BD 杆自重为 W 。
试画出图1 —4图a 所示为三角架结构 b 、c 、d 所示的隔离体的受力图 A zz ” X Xzr 'i/A1rC[------------DF AxAB虾F 或(a_2)1 — 6图示刚性构件 ABC 由销钉A 和拉杆GH 支撑,在构件的点C 作用有一水平力F 。
试问如果将力 F 沿其作用线移至点 D 或点E (如图示),是否会改变销钉 A 的受力状况。


eBook工程力学习题详细解答教师用书(第8章)2011-10-1范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan ,s Education & Teaching Studio习题8-1 习题8-2 习题8-3 习题8-4 习题8-5 习题8-6 习题8-7 习题8-8 习题8-9 习题8-10 习题8-9 习题8-10习题8-11 习题8-12 习题8-13 习题8-14 习题8-15 习题8-16 习题8-17 习题8-18 习题8-19 习题8-20习题8-21工程力学习题详细解答之八第8章 弯曲强度问题8-1 直径为d 的圆截面梁,两端在对称面内承受力偶矩为M 的力偶作用,如图所示。
若已知变形后中性层的曲率半径为ρ;材料的弹性模量为E 。
根据d 、ρ、E 可以求得梁所承受的力偶矩M 。
现在有4种答案,请判断哪一种是正确的。
(A) ρ64π4d E M =(B) 4π64d E M ρ=(C) ρ32π3d E M =(D) 3π32dE M ρ=正确答案是 A 。
8-2 矩形截面梁在截面B 处铅垂对称轴和水平对称轴方向上分别作用有F P1和F P2,且F P1=F P2,如图所示。
关于最大拉应力和最大压应力发生在危险截面A 的哪些点上,有4种答案,请判断哪一种是正确的。
(A) +max σ发生在a 点,−max σ发生在b 点M习题8-1图A Ba b cd P2z固定端习题8-2图(B) +max σ发生在c 点,−max σ发生在d 点 (C) +max σ发生在b 点,−max σ发生在a 点 (D) +max σ发生在d 点,−max σ发生在b 点正确答案是 D 。
8-3 关于平面弯曲正应力公式的应用条件,有以下4种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载;(B) 弹性范围内加载、载荷加在对称面或主轴平面内;(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;(D) 细长梁、载荷加在对称面或主轴平面内。
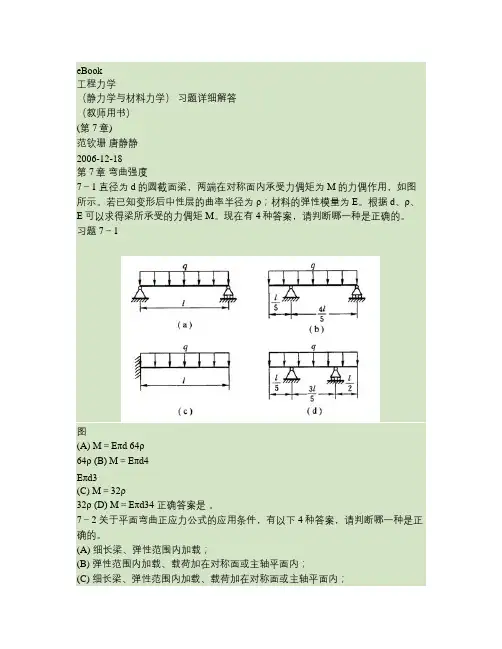
eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7-1 直径为d的圆截面梁,两端在对称面内承受力偶矩为M的力偶作用,如图所示。
若已知变形后中性层的曲率半径为ρ;材料的弹性模量为E。
根据d、ρ、E可以求得梁所承受的力偶矩M。
现在有4种答案,请判断哪一种是正确的。
习题7-1图(A) M=Eπd 64ρ64ρ (B) M=Eπd4Eπd3(C) M=32ρ32ρ (D) M=Eπd34 正确答案是。
7-2 关于平面弯曲正应力公式的应用条件,有以下4种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载;(B) 弹性范围内加载、载荷加在对称面或主轴平面内;(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7-3 长度相同、承受同样的均布载荷q作用的梁,有图中所示的4种支承方式,如果从梁的强度考虑,请判断哪一种支承方式最合理。
l 5习题7-3图正确答案是7-4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm。
求:梁的1-1截面上A、 2B两点的正应力。
习题7-4图解:1. 计算梁的1-1截面上的弯矩:M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1-1截面上A、B两点的正应力:A点:⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点:⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127-5 简支梁如图所示。
![工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩[1]](https://uimg.taocdn.com/5939f6a70029bd64783e2cf5.webp)

材料力学课后答案范钦珊第一篇:材料力学课后答案范钦珊材料力学课后答案范钦珊普通高等院校基础力学系列教材包括“理论力学”、“材料力学”、“结构力学”、“工程力学静力学材料力学”以及“工程流体力学”。
目前出版的是前面的3种“工程力学静力学材料力学”将在以后出版。
这套教材是根据我国高等教育改革的形势和教学第一线的实际需求由清华大学出版社组织编写的。
从2002年秋季学期开始全国普通高等学校新一轮培养计划进入实施阶段新一轮培养计划的特点是加强素质教育、培养创新精神。
根据新一轮培养计划课程的教学总学时数大幅度减少为学生自主学习留出了较大的空间。
相应地课程的教学时数都要压缩基础力学课程也不例外。
怎样在有限的教学时数内使学生既能掌握力学的基本知识又能了解一些力学的最新进展既能培养学生的力学素质又能加强工程概念。
这是很多力学教育工作者所共同关心的问题。
现有的基础教材大部分都是根据在比较多的学时内进行教学而编写的因而篇幅都比较大。
教学第一线迫切需要适用于学时压缩后教学要求的小篇幅的教材。
根据“有所为、有所不为”的原则这套教材更注重基本概念而不追求冗长的理论推导与繁琐的数字运算。
这样做不仅可以满足一些专业对于力学基础知识的要求而且可以切实保证教育部颁布的基础力学课程教学基本要求的教学质量。
为了让学生更快地掌握最基本的知识本套教材在概念、原理的叙述方面作了一些改进。
一方面从提出问题、分析问题和解决问题等方面作了比较详尽的论述与讨论另一方面通过较多的例题分析特别是新增加了关于一些重要概念的例题分析著者相信这将有助于读者加深对于基本内容的了解和掌握。
此外为了帮助学生学习和加深理解以及方便教师备课和授课与每门课材料力学教师用书lⅣ程主教材配套出版了学习指导、教师用书习题详细解答和供课堂教学使用的电子教案。
本套教材内容的选取以教育部颁布的相关课程的“教学基本要求”为依据同时根据各院校的具体情况作了灵活的安排绝大部分为必修内容少部分为选修内容。
习题9-38图 1-6 CABBBC9-38 加固后的吊车主梁如图所示。
梁的跨度l = 8m ,许用应力][σ= 100MPa 。
试分析当小车行走到什么位置时,梁内弯矩最大,并计算许可载荷(小车对梁的作用可视为集中力)。
解:1.小车行至梁中间时,梁内弯矩最大。
P P 1242F FM =⨯=82381103467.1)16367512675(21010755.1⨯=⨯⨯+⨯+⨯=z I mm 4 4351110113.8mm 10113.8166-⨯=⨯==z z I W m 3 ][11σ≤z W M ,即64P 1010010113.82⨯≤⨯-F 56.40P ≤F kN(1)2.小车行至离两端1.4 m 处P P2155.14.18)4.18(F F M =⨯-= 4110922.6-⨯=z W m 3][22σ≤z W M ,即64P 1010010922.6155.1+-⨯≤⨯F 9.59P ≤F kN (2)比较(1)、(2),得 [F P ] = 40.56 kN9-42 简支梁受力如图所示。
采用普通热轧工字型钢,且已知][σ= 160MPa 。
试确定工字型钢型号,并按最大切应力准则对梁的强度作全面校核。
解:1.F R A = F R B = 180kN (↑)75.885.010215.01802=⨯⨯-⨯==D C M M kN ·m100210215.116021802max =⨯⨯-⨯-⨯==M M E kN ·m175105.0180Q =⨯-=C F kN ][maxmax σσ≤=WM 463max 1025.61016010100][-⨯=⨯⨯=≥σM W m 3查型钢表,选工字钢No.32a :W = 692.2 cm 2,I z = 11075.5 cm 446.27=z z S IcmE 截面: 5.144maxmax ==WM σMPa 180175)kN (Q F AC1515BD175E ACEDB88.7588.75100M m-kN(a)习题9-43图5.144313r =-=σσσMPa ][σ<2. A +、B -截面:691026.27105.910180233Q max =⨯⨯⨯⨯==--z z dI S F τMPa13824max 2max 3r ===ττσMPa ][σ<3.C -、D +截面: 2.1161010755.1101451075.88833=⨯⨯⨯⨯=--x σMPaMPa46.491010755.1105.9105.15215130101758393*=⨯⨯⨯⨯⨯⨯⨯⨯=⋅=τ---zzC xy dI S F Q6.1524223r =+=xy x τσσMPa ][σ<∴ 选No.32a 工字钢安全。
高教范钦珊材料力学习题集有答案HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】习题1-2图习题1-4图材料力学习题集第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
B 处固定。
关于其两端的约束力有四种答案。
试分析等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
习题2-1图第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A ))(d d Q x q x F =;Q d d F xM=; (B ))(d d Q x q x F -=,Q d d F xM-=; (C ))(d d Q x q x F -=,Q d d F xM=; (D ))(d d Q x q xF =,Q d d F xM-=。
正确答案是 B 。
2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中哪几种是正确的。
习题2-3图习题2-4图 (a-1) (b-1)(a-2) (b-2)2-3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ,如图所示。
AyF FBCAAxF 'F CCDCF FAxF DR F FACBDAyFFDR F A CBD Ax F Ay F(a-1)第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 sin cos j i F ααF F +=分力:11 cos i F αF x = , 11 sin j F αF y =投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b 两种情形下各物体的受力图,并进行比较。
习题1-2图1y F x1F 1yF α1x F yF (c ) 2x F 2y F 2y 2x 2x F 2y F F(d )比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
1-3 试画出图示各物体的受力图。
习题1-3图F AxF AyF D C B A B F或(a-2)FF AF DCA(a-1)BF AxF AAyF C(b-1)W F BD C AyF F(c-1)F F CB B F A或(b-2) αDAF ABCBFAx F AAyFDF DC αF1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图C F CAAF (e-1) BF FCDBOOx F OyF W1O F A(f-1)FF DCABBF(e-3)'F AOOxF OyF AW(f-2)AF 1F A1O(f-3)F AF BF AAF xB 2F'yB 2F'1(c-1)F A B1B F(b-1)Dy F DDx F yB F C2(b-2)xB 2F'1F 1F'yB 2F'B(b-3)B WDxF DCyB F'(c-2)AF A D GF CH F H (a)1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
材料力学第二版课后答案1. 弹性力学。
1.1. 什么是材料的弹性?材料的弹性是指材料在受力后能够恢复原状的性质。
当外力作用于材料上时,材料会发生形变,但在去除外力后,材料会恢复到原来的形状和尺寸。
1.2. 什么是胡克定律?胡克定律是描述弹性体在弹性变形时,应力和应变之间的关系。
它可以用数学公式表示为,σ = Eε,其中σ表示应力,E表示弹性模量,ε表示应变。
1.3. 什么是杨氏模量?杨氏模量是描述材料抗拉伸性能的指标,它表示单位面积内的拉应力增加一个单位的长度时,材料的伸长量。
杨氏模量的计算公式为,E = σ/ε。
2. 塑性力学。
2.1. 什么是材料的塑性?材料的塑性是指材料在受力后会发生永久性变形的性质。
当外力作用于材料上时,材料会发生塑性变形,去除外力后,材料无法完全恢复原状。
2.2. 什么是屈服点?屈服点是材料在受力过程中,应力-应变曲线上的一个特殊点,表示材料从弹性变形进入塑性变形的临界点。
在屈服点之后,材料会发生永久性变形。
2.3. 什么是材料的硬度?材料的硬度是指材料抵抗外力压入的能力。
硬度测试可以用来评价材料的耐磨性、耐压性等性能,常用的硬度测试方法包括洛氏硬度、巴氏硬度等。
3. 断裂力学。
3.1. 什么是断裂韧性?断裂韧性是材料抵抗断裂的能力。
它是指材料在受到外力作用时,能够吸收大量的能量而不发生断裂的能力。
3.2. 什么是脆性断裂?脆性断裂是材料在受力过程中,发生迅速、不可逆的断裂现象。
脆性断裂的特点是断裂前往往不伴随明显的塑性变形。
3.3. 什么是韧性断裂?韧性断裂是材料在受力过程中,发生缓慢、可逆的断裂现象。
韧性断裂的特点是断裂前伴随明显的塑性变形,能够吸收大量的能量。
4. 疲劳力学。
4.1. 什么是疲劳寿命?疲劳寿命是指材料在受到交变应力作用下,经过一定次数的循环载荷后发生疲劳断裂的次数。
4.2. 什么是疲劳强度?疲劳强度是指材料在受到交变应力作用下,能够承受的最大应力水平,也可以理解为材料的抗疲劳能力。
习题9-38图 1-6 CABBBC
9-38 加固后的吊车主梁如图所示。
梁的跨度l = 8m ,许用应力][σ= 100MPa 。
试分析当小车行走到什么位置时,梁内弯矩最大,并计算许可载荷(小车对梁的作用可视为集中力)。
解:1.小车行至梁中间时,梁内弯矩最大。
P P 1242F F
M =⨯=
823
81103467.1)16367512
675(21010755.1⨯=⨯⨯+⨯+⨯=z I mm 4 4351
110113.8mm 10113.8166
-⨯=⨯==
z z I W m 3 ][11σ≤z W M ,即
6
4
P 1010010113.82⨯≤⨯-F 56.40P ≤F kN
(1)
2.小车行至离两端1.4 m 处
P P
2155.14.18)
4.18(F F M =⨯-= 4110922.6-⨯=z W m 3
][22
σ≤z W M ,即64
P 1010010
922.6155.1+-⨯≤⨯F 9.59P ≤F kN (2)
比较(1)、(2),得 [F P ] = 40.56 kN
9-42 简支梁受力如图所示。
采用普通热轧工字型钢,且已知][σ= 160MPa 。
试确定工字型钢型号,并按最大切应力准则对梁的强度作全面校核。
解:1.F R A = F R B = 180kN (↑)
75.885.0102
1
5.01802=⨯⨯-⨯==D C M M kN ·m
1002102
1
5.116021802max =⨯⨯-⨯-⨯==M M E kN ·m
175105.0180Q =⨯-=C F kN ][max
max σσ≤=
W
M 46
3max 10
25.61016010100][-⨯=⨯⨯=≥σM W m 3
查型钢表,选工字钢No.32a :
W = 692.2 cm 2,I z = 11075.5 cm 4
46.27=z z S I
cm
E 截面: 5.144max
max ==
W
M σMPa 180
175)
kN (Q F A
C
15
15
B
D
175E A
C
E
D
B
88.7588.75
100
M m
-kN
(a)
习题9-43图
5.144313r =-=σσσMPa ][σ<
2. A +
、B -
截面:
691026.27105.9101802
33
Q max =⨯⨯⨯⨯==--z z dI S F τMPa
13824max 2
max 3r ===ττσMPa ][σ<
3.C -、D +
截面: 2.1161010755.1101451075.888
3
3=⨯⨯⨯⨯=
--x σMPa
MPa
46.4910
10755.1105.9105.15215130101758
3
9
3*
=⨯⨯⨯⨯⨯⨯⨯⨯=
⋅=
τ---z
z
C xy dI S F Q
6.15242
23r =+=xy x τσσMPa ][σ<
∴ 选No.32a 工字钢安全。
9-70 传动轴受力如图示。
若已知材料的][σ= 120MPa ,试设计该轴的直径。
解:T = F P r
5000P ==r
T
F N
受力图(a )
25002
1
P ===F F F Cy Ay N
危险面B :
M x = 500N ·m
37515.0=⨯=Cy z F M N ·m 不计剪力影响 ][223r σσ≤+=W M M x
z
63
2
210120π50037532⨯≤+d
037575.0≥d m
取 d = 37.6mm
9-73 直杆AB 与直径d = 40mm 的圆柱焊成一体,结构受力如图所示。
试确定点a 和点b
的应力状态,
习题9-70图
A
B
C
y
T
T
D
P
F Cy F Ay
F z
(a)
A
A
B
B
C
A
x
M z
M D
m
375N ⋅m 500N ⋅
(a)
F R A
F R B
习题9-74图
并计算4r σ。
解:1.5N -=x F kN ,400-=ay F N 60150.0)6001000(=⨯-=x M N ·m 110275.0)6001000(-=⨯--=z M N ·m
2. 53.131032
40
π110
10440π10593623N =⨯⨯+⨯⨯⨯-=+=
--z z x a W M A F σMPa 7746.4P
==W M
x a τMPa
86.157746.4353.133222
24r =⨯+=+=a a τσσMPa
a 点应力状态如图(a )。
3. 979.3104
40π1056
23
N -=⨯⨯⨯-==-A F x b σMPa 252.5104
40π400
23101640π60236
293
P =⨯⨯⋅+⨯⨯=+=--A F W M ay x b τMPa 93.932
24r =+=b b τσσMPa
b 点应力状态如图(b )。
习题9-73图
a σa
τb
σb
τ
(a) (b)。