材料力学习题详解(范钦珊)第12章
- 格式:pdf
- 大小:1.04 MB
- 文档页数:17
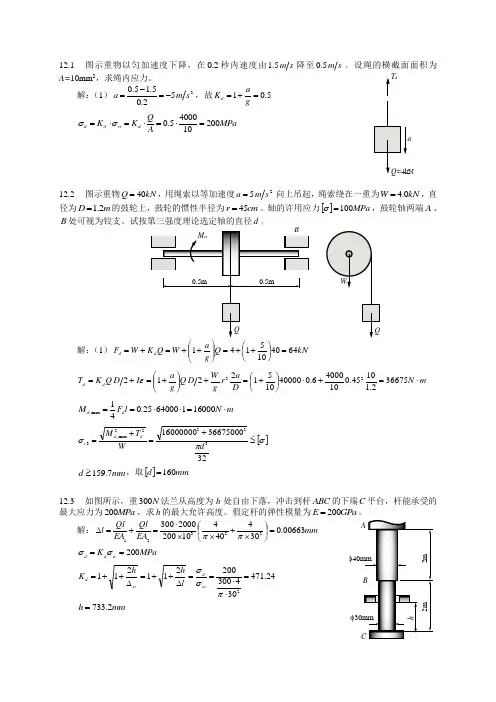
12.1 图示重物以匀加速度下降,在2.0秒内速度由s m 5.1降至s m 5.0。
设绳的横截面面积为A=10mm 2,求绳内应力。
解:(1)252.05.15.0s m a -=-=,故5.01=+=g a K dMPa A Q K K d st d d 2001040005.0=⋅=⋅=⋅=σσ12.2 图示重物kN Q 40=,用绳索以等加速度25s m a =向上吊起,绳索绕在一重为kN W 0.4=,直径为m D 2.1=的鼓轮上,鼓轮的惯性半径为cm r 45=。
轴的许用应力[]MPa 100=σ,鼓轮轴两端A 、B解:(1)kN Q g a W Q K W F d d 6440105141=⎪⎭⎫ ⎝⎛++=⎪⎪⎭⎫ ⎝⎛++=+= m N D a r g W D Q g a I D Q K T d d ⋅=+⋅⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫ ⎝⎛+=+=366752.11045.01040006.0400001051221222ε m N l F M d d ⋅=⋅⋅==1600016400025.041max , []σπσ≤+=+=32366750001600000032222max ,3d WT M d d rmm d 7.159≥,取[]mm d 160=12.3 如图所示,重N 300法兰从高度为h 处自由下落,冲击到杆ABC 的下端C 平台,杆能承受的最大应力为MPa 200,求h 的最大允许高度。
假定杆的弹性模量为E 200=解:mm EA Ql EA Ql l 00663.030440410200200030022321=⎪⎭⎫ ⎝⎛⨯+⨯⨯⋅=+=∆ππ MPa K st d d 200==σσ24.4713043002002112112=⋅⋅==∆++=∆++=πσσst d st d l h h K mm h 2.733=12.4 如图所示,重N 100物体从mm h 500=位置自由下落到铝制梁AB 上的C 点,求截面C 的位移和梁上的最大应力。


材料力学范钦珊答案1. 弹性力学1.1 弹性模量弹性模量是描述材料抵抗力学变形的能力的一个重要参数。
弹性模量E可以表示为材料的应力和应变之间的比例关系,计算公式如下:E = (σ / ε)其中,E是弹性模量,σ是应力,ε是应变。
在弹性力学中,当材料受到力的作用时,会发生弹性变形,即材料在去除力后能够回复原状。
弹性模量越大,材料的刚性越高,抵抗变形的能力越强。
1.2 剪切模量剪切模量描述了材料在受到剪切应力时抵抗剪切变形的能力。
剪切模量G可以表示为剪切应力和剪切应变之间的比例关系,计算公式如下:G = (τ / γ)其中,G是剪切模量,τ是剪切应力,γ是剪切应变。
剪切模量越大,材料的抗剪切能力越强。
1.3 泊松比泊松比描述了材料在受到应力时,沿着应力方向的变形与垂直于应力方向的变形之间的比例关系。
泊松比ν可以表示为侧向应变和纵向应变之间的比例关系,计算公式如下:ν = (-ε横/ ε纵)其中,ν是泊松比,ε横是侧向应变,ε纵是纵向应变。
泊松比的取值范围在0和0.5之间,材料越接近0.5,其纵向应变和侧向应变之间的耦合效应越强。
2. 拉伸性能材料的拉伸性能指的是材料在受到拉伸应力时的响应能力。
常见的拉伸性能参数包括杨氏模量、屈服强度、抗拉强度和伸长率。
2.1 杨氏模量杨氏模量描述了材料在拉伸应力作用下的线弹性变形能力。
杨氏模量可以表示为应力和应变之间的比例关系,计算公式如下:E = (σ / ε)其中,E是杨氏模量,σ是应力,ε是应变。
杨氏模量越大,材料的刚性越高,抵抗变形的能力越强。
2.2 屈服强度材料的屈服强度是指材料在拉伸过程中开始出现塑性变形的应力值。
在应力达到屈服强度之后,材料会发生塑性变形,即无法完全恢复原状。
屈服强度通常用σy表示。
2.3 抗拉强度材料的抗拉强度是指材料在拉伸过程中能够承受的最大应力值。
抗拉强度通常用σmax表示。
2.4 伸长率伸长率描述了材料在拉伸过程中发生塑性变形后的延展性能。


材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
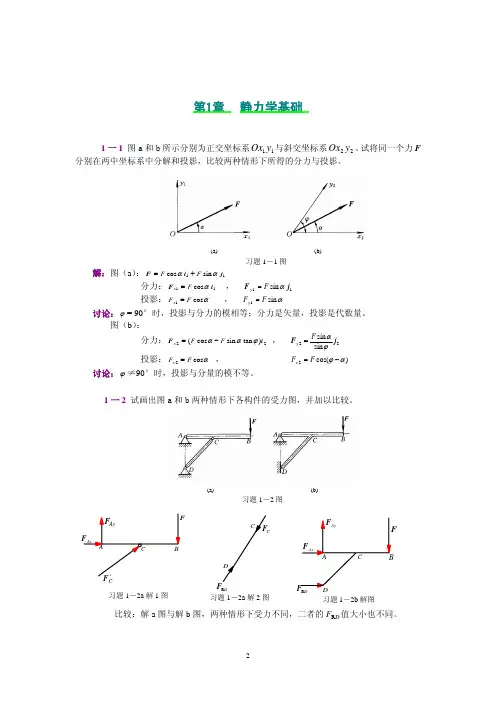
(a) (b) 习题1-1图第1章 静力学基础1一1 图a 和b 所示分别为正交坐标系11y Ox 与斜交坐标系22y Ox 。
试将同一个力F 分别在两中坐标系中分解和投影,比较两种情形下所得的分力与投影。
解:图(a ):11 sin cos j i F ααF F +=分力:11 cos i F αF x = , 11 sin j F αF y = 投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
图(b ): 分力:22)tan sin cos (i F ϕααF F x −= , 22sin sin j F ϕαF y =投影:αcos 2F F x = , )cos(2αϕ−=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1一2 试画出图a 和b 两种情形下各构件的受力图,并加以比较。
比较:解a 图与解b 图,两种情形下受力不同,二者的F R D 值大小也不同。
DR习题1-2b 解图DR习题1-2a 解2图C习题1-2a 解1图(a) (b)习题1-2图1一3 试画出图示各构件的受力图。
习题1-3图B F 习题1-3a 解2图 B习题1-3a 解1图习题1-3b 解1图F Ay Ax 习题1-3c 解图 A习题1-3b 解2图习题1-3d 解1图习题1-3e 解1图习题1-3e 解2图1-4 图a 所示为三角架结构。
荷载F 1作用在B 铰上。
AB 杆不计自重,BD 杆自重为W ,作用在杆的中点。
试画出图b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1习题1-3f 解1图F习题1-3e 解3图'A习题1-3f 解2图1O 习题1-3f 解3图F F'F 1习题1-4d 解2图F y B 21习题1-4c 解1图 AA B 1B FDx y2B 习题1-4b 解2图 1习题1-4b 解3图 F y B 2习题1-4c 解2图 F A B1B FAxF'习题1-5b 解3图E D(a-3)E B F习题1-5b 解2图习题1-5b 解1图'AxFF B习题1-5c 解图1一5 试画出图示结构中各杆的受力图。

56 第十二章 动载荷第十二章 动载荷第十二章答案12.1 吊索以匀加速度a = 4.9m/s 2提升重F = 20kN 的重物,吊索的许用应力〔σ〕= 80MPa ,试求吊索的最小横截面面积。
N F F ma -=, 4.92020309.8N F =+⨯=kN []NF Aσσ=≤ 3463010 3.75108010A -⨯≥=⨯⨯m 2.12.2 用两根平行钢索,以匀加速度a =9.8m/s 2提升图示工字钢梁(型号:32c ),试求梁的最大动应力。
由惯性力引起的载荷密度:q 2=ma /l=62.765la lq =62.765g +62.765a 666262.7659.81090.9081.210M W σ--⨯⨯⨯==⨯=⨯MPa.12.3 直径d 1=30cm ,长l =6m 弹性模量E 1 = 10GPa 的二相同木杆。
重W =5kN 的重锤从杆的上部H =1m 高度处自由落下,其中杆b 顶端放一直径d =15cm ,厚h =20mm ,弹性模量E 2 = 8 MPa 的橡皮垫。
试求二杆的应力。
(1) 3592510644.2441010100.3st Pl EA π-⨯⨯⨯∆===⨯⨯⨯⨯m 1511093.0d F P ⎛⎛=== ⎝⎝kN 36210931041015.460.3d d F A σπ-⨯⨯==⨯=⨯MPa. (2) 橡皮垫的静位移:342625100.0247.0736108100.15st π-⨯⨯⨯∆==⨯⨯⨯⨯m 总的静位移:5444.244107.0736107.49810st ---∆=⨯+⨯=⨯maF( a )( b )第十二章 动载荷 5751260d F ⎛== ⎝kN 362260.710410 3.690.3d σπ-⨯⨯=⨯=⨯MPa. 12.4 图示装置,直径d = 4cm ,长l = 4m 的钢杆,上端固定,下端有一托盘,钢杆的弹性模量 E = 200GPa,许用应力〔σ〕=120MPa,弹簧刚度k =160kN/cm,自由落体重P = 20kN,试求容许高度h 为多少。
C(a-2)DR(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 s i n c o s j i F ααF F +=分力:11 cos i F αF x = , 11 s i n j F αF y =投影:αcos 1F F x = , αs i n 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b习题1-2图比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
(c )2x(d )1-3 试画出图示各物体的受力图。
习题1-3图B或(a-2)(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D ,则A 端受力改变,因为HG 与ABC 为不同的刚体。
1(f-1)'A(f-2)1(f-3)F F'F 1(d-2)AF yB 21(c-1)F A B1FDx y(b-2)1(b-3)F yB 2 F A B1B F习题1-5图AxF'(b-3)E D(a-3)B(b-2)(b-1)F 'CDDF EFBC(c)AxF1-6 试画出图示连续梁中的AC 和CD 梁的受力图。
eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7-1 直径为d的圆截面梁,两端在对称面内承受力偶矩为M的力偶作用,如图所示。
若已知变形后中性层的曲率半径为ρ;材料的弹性模量为E。
根据d、ρ、E可以求得梁所承受的力偶矩M。
现在有4种答案,请判断哪一种是正确的。
习题7-1图(A) M=Eπd 64ρ64ρ (B) M=Eπd4Eπd3(C) M=32ρ32ρ (D) M=Eπd34 正确答案是。
7-2 关于平面弯曲正应力公式的应用条件,有以下4种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载;(B) 弹性范围内加载、载荷加在对称面或主轴平面内;(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7-3 长度相同、承受同样的均布载荷q作用的梁,有图中所示的4种支承方式,如果从梁的强度考虑,请判断哪一种支承方式最合理。
l 5习题7-3图正确答案是7-4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm。
求:梁的1-1截面上A、 2B两点的正应力。
习题7-4图解:1. 计算梁的1-1截面上的弯矩:M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1-1截面上A、B两点的正应力:A点:⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点:⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127-5 简支梁如图所示。
高教范钦珊材料力学习题集有答案HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】习题1-2图习题1-4图材料力学习题集第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
B 处固定。
关于其两端的约束力有四种答案。
试分析等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
习题2-1图第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A ))(d d Q x q x F =;Q d d F xM=; (B ))(d d Q x q x F -=,Q d d F xM-=; (C ))(d d Q x q x F -=,Q d d F xM=; (D ))(d d Q x q xF =,Q d d F xM-=。
正确答案是 B 。
2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中哪几种是正确的。
习题2-3图习题2-4图 (a-1) (b-1)(a-2) (b-2)2-3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ,如图所示。