小学六年级---比和比例

《比和比例》具体内容及教学建议编写意图（1）教材首先以小精灵提问的方式，引导学生复习比和比例的基础知识，比较它们的联系与区别。

通过例1，借助表格梳理，引导学生重温比和比例的意义、各部分名称和基本性质，体现让学生自主归纳的思想。

（2）例2，仍然借助表格的方式，梳理比和分数、除法的关系，把学生分散的知识点进行整合，学会整体地、一般性地把握知识，使知识融会贯通，体会变中有不变的思想。

（3）例3，让学生回顾比的基本性质、分数的基本性质、商不变的规律之间的联系，揭示三者之间的密切联系和内在一致性。

（4）例4，让学生复习正比例关系、反比例关系的概念，并通过生活中的实例说明两种量成正、反比例的判断方法，培养学生的函数思想。

教学建议（l）引导学生进行自主复习。

本节内容几乎涵盖了比和比例的全部知识点，教师可要求学生在课前对本节内容进行自主归纳与整理，形成知识体系。

例如，让学生梳理比、比例、正（反）比例的前后承接关系，了解概念的逐步发展。

通过课上交流，把自己整理过程中不够完备的地方进行补充、完善。

（2）引导学生发现概念之间的联系与区别，形成知识网络。

除了让学生理清前面所述的比、比例、正（反）比例的概念之间的关系以外，还要像例2、例3那样，把相关的概念、性质放在一起进行整理，使学生看到不同形式背后的一致性。

如例2，除了让学生交流展示自己整理的结果，还可追问：能用一个式子来表示三者之间的关系吗？即ab＝a÷b＝a：b（b≠0），并由此引出例3的问题，将表面上看似不同的三个知识整合为本质相同的“一个知识”。

（3）加强函数思想的教学。

例4，通过实例理解、描述正、反比例的概念时，要注意强调“前提”，即在什么前提下，哪两个量成正比例关系？在什么前提下，哪两个量成反比例关系？。

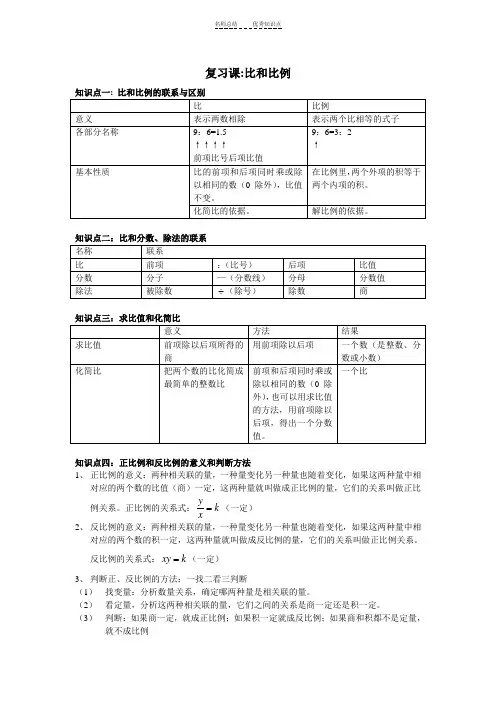
复习课:比和比例知识点三：求比值和化简比 知识点四：正比例和反比例的意义和判断方法1、 正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

正比例的关系式：k xy=（一定） 2、 反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。

反比例的关系式：k xy =（一定）3、 判断正、反比例的方法：一找二看三判断（1） 找变量：分析数量关系，确定哪两种量是相关联的量。

（2） 看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。

（3） 判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量，就不成比例知识点五：用比例知识解决问题1、按比例分配问题（1）按比例分配应用题：把一个量按照一定的比分配成几部分，求每个部分数量各是多少的应用题叫做按比例分配应用题。

（2）解题方法一般方法：把比转化成为分数，用分数方法解答，即先求出总分数，然后求出各部分量占总量的几分之几，最后按照求一个数的几分之几多少的解题方法，分别求出各部分的量是多少归一法：把比看做分得的分数，先求出各部分的总分数，然后再用“总量÷总份数=平均每份的量（归一）”，再用“一份的量⨯各部分量所对应的份数”，求出各部分的量。

用比例知识解答：首先设未知量为。

再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式，再解比例求出x。

2、用正、反比例知识解答应用题的步骤（1）分析数量关系。

判断成什么比例。

（２）找等量关系。

如果成正比例，则按等比找等量关系式；如果成反比例，则按等积找等量关系式。

（３）解比例式。

设未知数为x，并代入等量关系式，得正比例式或反比例式。

（４）解比例。

（５）检验并写出答语。

小学六年级--比和比例知识点梳理复习课:比和比例知识点一: 比和比例的联系与区别知识点二：比和分数、除法的联系知识点三：求比值和化简比知识点四：正比例和反比例的意义和判断方法1、正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

正比例的关系式：k xy=（一定）2、反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。

反比例的关系式：kxy=（一定）3、判断正、反比例的方法：一找二看三判断（1）找变量：分析数量关系，确定哪两种量是相关联的量。

（2）看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。

（3）判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量，就不成比例4、正比例、反比例的区别与联系知识点五：用比例知识解决问题1、按比例分配问题（1）按比例分配应用题：把一个量按照一定的比分配成几部分，求每个部分数量各是多少的应用题叫做按比例分配应用题。

（2）解题方法一般方法：把比转化成为分数，用分数方法解答，即先求出总分数，然后求出各部分量占总量的几分之几，最后按照求一个数的几分之几多少的解题方法，分别求出各部分的量是多少归一法：把比看做分得的分数，先求出各部分的总分数，然后再用“总量÷总份数=平均每份的量（归一）”，再用“一份的量⨯各部分量所对应的份数”，求出各部分的量。

用比例知识解答：首先设未知量为。

再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x 的比例式，再解比例求出x 。

2、用正、反比例知识解答应用题的步骤（1）分析数量关系。

判断成什么比例。

（２）找等量关系。

如果成正比例，则按等比找等量关系式；如果成反比例，则按等积找等量关系式。

六年级数学《比和比例》知识点一、比的意义和性质1、比的意义两个数相除又叫做两个数的比。

2、比的性质比的前项和后项同时乘上或者除以相同的数（0除外），比值不变。

3、比的应用通过比可以应用一些问题。

二、比例的意义和性质1、比例的意义表示两个比相等的式子叫做比例。

2、比例的性质在一个比例中，组成比例的两个数，叫做比例的项。

在一比例里，两外项的积等于两内项的积。

这叫做比例的基本性质。

3、解比例根据比例的基本性质，如果已知比例中的任何三项，就可以求出这个比例中的另外一个未知项。

这个求未知项的过程，叫做解比例。

三、正比例和反比例1、成正比例的量如果两种量是相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值一定，这两种量就叫做成正比例的量。

2、成反比例的量如果两种量是相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量。

3、正比例和反比例的判断方法判断两种量是否成正比例或反比例的方法：一是看这两种相关联的量中相对应的两个数的比值是否一定；二是看这两种量中相对应的两个数的积是否一定。

比的意义：两个量的关系可以用比来表示，我们通常称之为“比”。

定义：在两个量的比中，我们把数量放在前面，单位“1”放在后面，我们称之为前项，后项。

比与除法、分数的关系：比的前项相当于被除数或分子，后项相当于除数或分母，比值相当于商或分数值。

比的性质：比的前项和后项同时乘上或者除以相同的数(0除外)，比值不变。

比例的意义：表示两个比相等的式子叫做比例。

组成比例的四个数叫做比例的项。

两外两项叫做内项，中间两项叫做外项。

如果中间的两项是两个相同的数，这样的比例叫做对称比例。

比例尺的意义：我们把图上距离和实际距离的比叫做比例尺。

我们把比例尺分为放大比例尺和缩小比例尺两种。

缩小比例尺的计算方法：已知实际距离求图上距离，根据公式计算即可；已知图上距离求实际距离根据公式计算即可。

1、比的意义和性质
（1）比的意义：两个数相除又叫做两个数的比。

“：”是比号，读作“比”。

比号前面的数叫做比的前项，比号后面的
数叫做比的后项。

比的前项除以后项所得的商，叫做比值。

同除法比较，比的前项相当于被除数，后项相当于除数，比值相当于商。

比值通常用分数表示，也可以用小数表示，有时也可能是整数。

比的后项不能是零。

根据分数与除法的关系，可知比的前项相当于分子，后项相当于分母，比值相当于分数值。

（2）比的性质
比的前项和后项同时乘上或者除以相同的数（0 除外），比值不变，这叫做比的基本性质。

（3）求比值和化简比
求比值的方法：用比的前项除以后项，它的结果是一个数值可以
是整数，也可以是小数或分数。

根据比的基本性质可以把比化成最简单的整数比。

它的结果必须是一个最简比，
2、比例的意义和性质
（1）比例的意义表示两个比相等的式子叫做比例。

组成比例的四个数，叫
做比例的项。

两端的两项叫做外项，中间的两项叫做内项。

（2）比例的基本性质
在比例里，两个外项的积等于两个两个内向的积。

（3）解比例
根据比例的基本性质，如果已知比例中的任何三项，就可以求出这个
数比例中的另外一个未知项。

求比例中的未知项，叫做解比例。

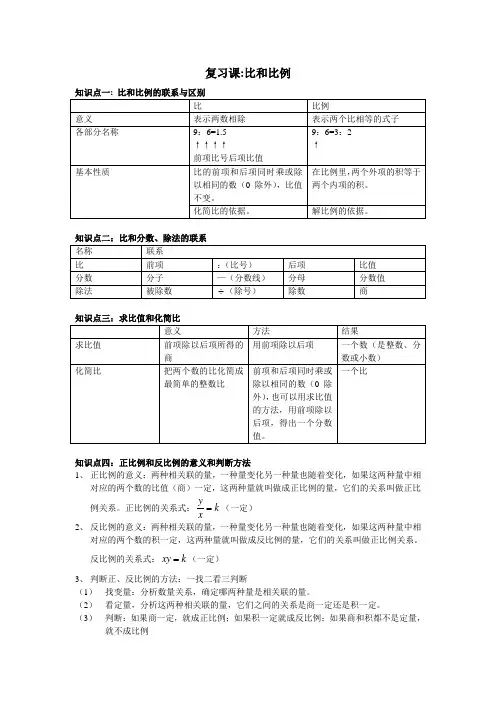
复习课:比和比例知识点三：求比值和化简比 知识点四：正比例和反比例的意义和判断方法1、 正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

正比例的关系式：k xy=（一定） 2、 反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。

反比例的关系式：k xy =（一定）3、 判断正、反比例的方法：一找二看三判断（1） 找变量：分析数量关系，确定哪两种量是相关联的量。

（2） 看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。

（3） 判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量，就不成比例知识点五：用比例知识解决问题1、按比例分配问题（1）按比例分配应用题：把一个量按照一定的比分配成几部分，求每个部分数量各是多少的应用题叫做按比例分配应用题。

（2）解题方法一般方法：把比转化成为分数，用分数方法解答，即先求出总分数，然后求出各部分量占总量的几分之几，最后按照求一个数的几分之几多少的解题方法，分别求出各部分的量是多少归一法：把比看做分得的分数，先求出各部分的总分数，然后再用“总量÷总份数=平均每份的量（归一）”，再用“一份的量⨯各部分量所对应的份数”，求出各部分的量。

用比例知识解答：首先设未知量为。

再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式，再解比例求出x。

2、用正、反比例知识解答应用题的步骤（1）分析数量关系。

判断成什么比例。

（２）找等量关系。

如果成正比例，则按等比找等量关系式；如果成反比例，则按等积找等量关系式。

（３）解比例式。

设未知数为x，并代入等量关系式，得正比例式或反比例式。

（４）解比例。

（５）检验并写出答语。

比和比例（1）
2、某校合唱队与舞蹈队人数之比为3 ：2，如果将合唱队的队员调10名到舞蹈队，
那么这时的人数比为7 ：8，原合唱队有人
3、甲、乙、丙三人外出参观。

午餐时，甲带有4包点心，乙带有3包点心，丙带有
7元钱却没有买到食物，他们决定把甲、乙二人的点心平均分成三份食用，由丙把7元钱还给甲和乙，那么，甲应分得元
@
4、三个容积相同的瓶子装满酒精溶液，酒精与水的比分别是3 ：2, 3 ：1, 4 ：1,
当把三瓶酒精溶液混合时，酒精与水的比是
5、有甲、乙、丙三个长方体，它们的长之比是2 ：2 ：3，宽之比是3 ：5 ：6，高之比是6 ：2 ：5，如果丙的体积是90立方厘米，那么甲、乙两个长方体的体积之和是
立方厘米。

比和比例（2）
3．4．
5．6．
比和比例（3）
比和比例（4）。

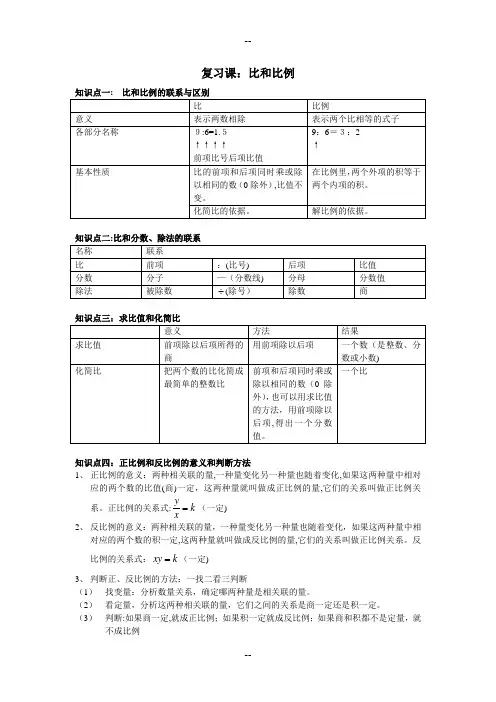
复习课：比和比例知识点三：求比值和化简比 知识点四：正比例和反比例的意义和判断方法1、 正比例的意义：两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定，这两种量就叫做成正比例的量,它们的关系叫做正比例关系。

正比例的关系式:k xy=（一定) 2、 反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。

反比例的关系式：k xy =（一定)3、 判断正、反比例的方法：一找二看三判断（1） 找变量：分析数量关系，确定哪两种量是相关联的量。

（2） 看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。

（3） 判断:如果商一定,就成正比例；如果积一定就成反比例；如果商和积都不是定量，就不成比例知识点五：用比例知识解决问题1、按比例分配问题（1）按比例分配应用题:把一个量按照一定的比分配成几部分，求每个部分数量各是多少的应用题叫做按比例分配应用题。

（2）解题方法一般方法:把比转化成为分数,用分数方法解答，即先求出总分数，然后求出各部分量占总量的几分之几,最后按照求一个数的几分之几多少的解题方法，分别求出各部分的量是多少归一法：把比看做分得的分数,先求出各部分的总分数,然后再用“总量÷总份数＝平均每份的量（归一)”,再用“一份的量⨯各部分量所对应的份数”,求出各部分的量。

用比例知识解答:首先设未知量为。

再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有ｘ的比例式，再解比例求出x。

2、用正、反比例知识解答应用题的步骤（1）分析数量关系。

判断成什么比例。

（2)找等量关系。

如果成正比例，则按等比找等量关系式；如果成反比例,则按等积找等量关系式。

（３）解比例式。

设未知数为x，并代入等量关系式,得正比例式或反比例式。

(4）解比例。

（5)检验并写出答语。

小学六年级--比和比例知识点梳理work Information Technology Company.2020YEAR复习课:比和比例知识点二：比和分数、除法的联系 知识点三：求比值和化简比知识点四：正比例和反比例的意义和判断方法1、正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

正比例的关系式：k xy=（一定）2、反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。

反比例的关系式：kxy=（一定）3、判断正、反比例的方法：一找二看三判断（1）找变量：分析数量关系，确定哪两种量是相关联的量。

（2）看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。

（3）判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量，就不成比例4、正比例、反比例的区别与联系知识点五：用比例知识解决问题1、按比例分配问题（1）按比例分配应用题：把一个量按照一定的比分配成几部分，求每个部分数量各是多少的应用题叫做按比例分配应用题。

（2）解题方法一般方法：把比转化成为分数，用分数方法解答，即先求出总分数，然后求出各部分量占总量的几分之几，最后按照求一个数的几分之几多少的解题方法，分别求出各部分的量是多少归一法：把比看做分得的分数，先求出各部分的总分数，然后再用“总量÷总份数=平均每份的量（归一）”，再用“一份的量⨯各部分量所对应的份数”，求出各部分的量。

用比例知识解答：首先设未知量为。

再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x 的比例式，再解比例求出x 。

2、用正、反比例知识解答应用题的步骤（1）分析数量关系。

判断成什么比例。

（２）找等量关系。

如果成正比例，则按等比找等量关系式；如果成反比例，则按等积找等量关系式。

复习课：比和比例知识点一：比和比例的联系与区别知识点四：正比例和反比例的意义和判断方法1、正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

正比例的关系式：上k （一定）x2、反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。

反比例的关系式：xy k （一定）3、判断正、反比例的方法：一找二看三判断（1）找变量：分析数量关系，确定哪两种量是相关联的量。

（2）看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。

（3）判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量, 就不成比例知识点五：用比例知识解决问题1、按比例分配问题（1）按比例分配应用题：把一个量按照一定的比分配成几部分，求每个部分数量各是多少的应用题叫做按比例分配应用题。

（2）解题方法一般方法：把比转化成为分数，用分数方法解答，即先求出总分数，然后求出各部分量占总量的几分之几，最后按照求一个数的几分之几多少的解题方法，分别求出各部分的量是多少归一法：把比看做分得的分数，先求出各部分的总分数，然后再用“总量总份数=平均每份的量（归一）”，再用“一份的量各部分量所对应的份数”，求出各部分的量。

用比例知识解答：首先设未知量为。

再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式，再解比例求出X。

2、用正、反比例知识解答应用题的步骤（1 ）分析数量关系。

判断成什么比例。

（2）找等量关系。

如果成正比例，则按等比找（3）解比例式。

设未知数为X, 等量关系式；如果成反比例，则按等积找等量关系式。

并代入等量关系式，得正比例式或反比例式。

（4）解比例。

（5）检验并写出答语。

精讲典型题例题1（1）一项工程，甲单独做要4 天，乙单独做要5 天完成，甲和乙的工作效率比是（）（）（2）把2 米：4 厘米化成最简单的整数比是（），比值是（）。

《比和比例整理与复习》说课稿龙台小学李慧勤各位老师：大家好！今天我说课的内容是西师版小学六年级下册第五单元总复习中的《比和比例》。

我将分以下五个部分进行说课：一、对本课教材的理解和思考二、学情分析三、对教学目标和重难点的把握四、对教学设计的思考五、对教法、学法的理解六、说教学过程首先说说教材，《比和比例》这部分内容主要是复习比和比例的意义与性质，比和分数、除法的关系，正反比例的应用及判断，以及比和比例的一些应用。

比例尺及其应用，在后面的“空间与图形”中进行复习。

但本班学生的基础不是很好，正反比例的应用及判断，以及比和比例的一些应用”这部分知识放在第二课时进行。

毕业班的复习课注重帮助学生把分散在各年级、各章节中有关的数学知识上下串联，左右沟通起来。

理清知识体系要充分调动学生的主动性和积极性，要让学生自己动手动脑，教师的作用主要是引导、帮助、点拨和补充二、学情分析：数学的复习过程，其实就是学生的知识不断重组，并形成良好的认知结构的过程。

在此过程中，学生的自主整理和构建知识网络的能力就显得特别重要。

因为是整理复习课，所以课堂教学中就应尽量让学生自己动手、动脑对学习的知识内容进行搜集、整理、归纳，通过开展讨论交流、分析比较等学习形式，感受到不同知识之间的内在联系以及异同，体会数学知识在不同实际问题中的应用，使学生在实践、思考教学目标等自主学习的过程中巩固知识、培养能力、形成技能。

本节课学生对比和比例、比的基本性质和比例的基本性质、化简比和求比值等知识点容易混淆，灵活运用知识能力欠缺。

三、教学目标、教学重难点。

【教学目标】：1、加强对比和比例这节知识间的联系，整理形成知识框架，使之系统化。

2、在具体的实际问题情境中，复习比和比例的含义及性质，会正确的化简比和求比值，解比例。

3、培养复习总结的好习惯，渗透事物间相互联系的辩证唯物主义观点。

【教学重点】：理解比和比例的意义、性质，掌握关于比和比例的一些实际运用和计算。

复习(fùxí)课:比和比例知识(zhī shi)点一: 比和比例(bǐlì)的联系与区别比比例意义表示两数相除表示两个比相等的式子各部分名称9：6=1.5↑↑↑↑前项比号后项比值9：6=3：2↑基本性质比的前项和后项同时乘或除以相同的数（0除外），比值不变。

在比例里，两个外项的积等于两个内项的积。

化简比的依据。

解比例的依据。

知识点二：比和分数(fēnshù)、除法的联系名称联系比前项：（比号）后项比值分数分子—（分数线）分母分数值除法被除数（除号）除数商知识点三：求比值(bǐzhí)和化简比意义方法结果求比值前项除以后项所得的商用前项除以后项一个数（是整数、分数或小数）化简比把两个数的比化简成最简单的整数比前项和后项同时乘或除以相同的数（0除外），也可以用求比值的方法，用前项除以后项，得出一个分数值。

一个比知识点四：正比例和反比例的意义和判断方法1、正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

正比例的关系式：（一定）2、反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。

反比例的关系式：（一定）3、判断正、反比例的方法：一找二看三判断（1）找变量：分析数量关系，确定哪两种量是相关联的量。

（2）看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。

（3）判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量，就不成比例4、正比例、反比例的区别与联系名称不同点相同点意义不相同变化方向不相同关系式不同正比例两种量中相对应的两个数的比值，也就是商一定一种量扩大（或缩小），另一种量也随之扩大（或缩小）。

kxy=（一定）两种相关联的量，一种量变化另一种量也随着变化反比例两种量中相对应的两个数的积一定一种量扩大（或缩小），另一种量也随之缩小（或扩大）。

知识点一：认识比1、两个数相除又叫两个数的比,任何两个相关数量的比都可以抽象为两个数的比。

知识点二：比、除法、分数的关系2、比、除法、分数之间的联系：知识点三：比值的计算方法3、计算方法：求两个数的比的比值,就是用比的前项除以后项。

4、比和比值的区别：（1）比表示的是两个数的一种关系；比值是一个数值； （2）比可以写成bab a 或:的形式；比值可以是分数、小数或整数。

知识点四：比的基本性质5、比的前项、后项同时乘或除以相同的数（0除外）,比值不变。

这叫做比的基本性质。

知识点五：化简比6、如果比的前项和后项都是整数,化简时可直接把比的前项和后项同时除以它们的最大公因数。

比 前项 比号 后项 比值 除法 被除数 除号 除数 商 分数 分子分数线分母分数值比和比例知识归纳提示：在以后解决问题或计算时,求两个数或几个数的比,如果没有特殊要求,一般要求出最简单的整数比。

知识点六：比例的意义7、比例的意义：表示两个比相等的式子叫做比例。

比例中有两个内项和两个外项。

拓展：比和比例的联系：比例是由比组成的。

比和比例的区别：（1）意义不同,比表示两个数相除的关系；比例表示两个比相等的关系 （2）形式不同,比由两项组成,比例由四项组成。

知识点七：比例的基本性质8、在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。

如果用字母表示比例的四个项,d c b a ::=,那么比例的基本性质可以表示成c b d a ⨯=⨯。

拓展：（1）根据比例的基本性质,可以判断两个比能否组成比例。

（2）组成比例的4个数最多可以组成8个不同的比例。

（3）根据比例的基本性质,已知比例中的任意三项,就可以求出第四项。

知识点八：解比例9、根据比例的基本性质,把两个外项和两个内项分别相乘,将比例式改写成c b d a ⨯=⨯的形式,再解方程求出x 的值。

【例1】 比的意义：一辆汽车3小时行驶了150千米,这辆汽车行驶的路程和时间的比是多少？比值是多少？比值表示什么？【练习】甲3小时走15千米,乙4小时走24千米。

复习课:比和比例知识点四=正比例和反比例的意义和判断方袪1.正比例的意义I两种相关联的量，一种量变化另一种量也随着变化.如果这两种量中相对应的两偉的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

正比例的关系式：^=k（一定）x2.反比例的意义，两种相关联的:t・一种宣变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定.这两种量就叫做成反比例的量.它们的关系叫做正比例关系。

反比例的关系式：工丁 =去〔一定）氛判断正、反比例的方法：一找二看三判断（1）找变量：分析数量关系.确定哪两种量是相关联的量，（H 看定量，分析这两种相关联的量，它们之间的关系是商一定还是和一定。

⑶ 判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量, 就不成比例和识点五,用比例知识解决问題1、按比例分配间题C1）按比例分配应用题；把一个量按昭一宦的比分配成几部分.求每个部分数量各是多少的应用题叫做按比例分配应用题。

（2）解题方法—般方注.把比转化成为分数、用分数方法解答，即先求岀总分数，然后求出各部分量占总量的几分之几，最后按照求一个数的几分之几多少的解題方法，分别求出各部分的量是多少归一法士把比看做分得的分数，先求岀各部分的总分数，然后再用“总量十总饴数讦均每份的量（归一）3再用“一份的量技各部分量所对应的份数X求出各部分的量。

用比例知识解答：苜先设未知量为。

再根据题中“已知比等于相对应的量的比■"作为等量关系式列岀含有x的比例式，再解比例求出“菽用正、反比例知识|军答应用题的步骤（I）分析数量关系*判断成什么比例。

找等量关系.如果成正比例，则按等比找等量关系式；如果成反比例，则按等积找等量关系式。

2）解比例式。

设未知数为* 并代入等量关系式，得正比例式或反比例式。

〔4）解比例。

（5 ）检验并写岀答语。

笫二讲比和比例在应用题的各种类型中，有一类与数量之间的〔正、反）比例关系有关. 在解答这类应用题时，我们需要对题中各个量之间的关系作岀正确的判断.成正比或反比的量中都有两种相关联的量.一种量〔记作Q变化时另一种量C记作y）也随着变化.与这两个量联系着.有一个不变的量（记为k）. 在判断变量E与涯否成正.反比例时，我们要紧紧抓住这个不变量b如果不变量k■是变量y与梵的商*即在梵变化时y与艺的商不变I —= k s那么y与梵成正比例J如果k是y与垃的积，即在X变化时，y与x的积匚浹：xy = k J那么y乐成反比例.如果这两个关系式都不成立，那么y与x不成〔正和反）比例.下面我们从最基本的判断两种量是否成比例的例题开始.例1下列各题中的两种量是否成比例？成什么比例？①速度一定，路程与时间.②路程一定，速度与时间.③路程一定，已走的路程与未走的路程.④总时间一定，要制造的零件总数和制造每个零件所用的时间.⑤总产量一定，亩产量和播种面积.⑥整除情况下被除数一定，除数和商.⑦同时同地，竿高和影长.⑧半径一定，圆心角的度数和扇形面积.⑨两个齿轮啮合转动时转速和齿数-⑪圆的半径和面积-（11）长方体体积一定，底面积和高.（12）正方形的边长和它的面积.(13)乘公共汽车的站数和票价•(1Q房间面积一定.每块地板砖的面积与用持的块数.(15)汽车行驶时每公里的耗油量一定，所行驶的距离和耗油总量.分析以上每题都是两种相关联的量，一种量变化，另一种量也随着变化，那么怎样来确定这两种量成哪神比例或不成比例呢？关键是能否把两个相关的变量濱萝用艺二k或用罗来表示，其中k是定量.如果不能写出这两X种形式，或只能写岀加减法关系，那么这两种量就不成比例例如① 講二速度，速度一定’路程与吋间成正比例*④制造每个零件用的时间X聽銘型走蠢豔篦勰鶴觀造蠶斜解’成正匕頃］的有：①、⑦、⑧、(15)成反比例的有’②、©.⑤、⑥、(11). (14)不成比例的有’③、⑪、(12). (13)，例2 -条路全长60千米.分成上坡、平路、下坡三段，各段路程长的比依次是X 2；3,某人走各段路程所用时间之比依次是4 ：5： 6.已知他上坡的速度是每小时汗氷，问此人建完全程埔了多少时间？分祈要求此人走完全程埔了多少时间，必须根据己知条件先求出此人走上坡路用了多少时间，必须知道走上坡路的速度〔题中每小时行3千米)和上坡路的路程，已知全程60千氷又知道上坡、平路、下坡三段路程比是「2 : 3,就可以求出上坡路的路程.解’上坡路的路程：60X匸吕轩=10 (千米)・走上坡路用的时间：10^3 = 3^ （小时）.上坡路所用时间与全程所用时间比;走完全程所用时间:^ = 12^ （小时）.答：此人走完全程共用12+小时.例3 —块合金内铜和锌的比是2： 3,现在再加入6克锌，共得新合金36 克，求新合金内铜和锌的比？分析要求新合金内铜和锌的比，必须分别求出新合金内铜和锌各自的重量.应该注意到铜和锌的比是2：3时，合金的重量不是盹克，而是（36-6）克.铜馬重量始终没崔变*解；铜和锌的比是2：对，合金重量’36-6 = 30 （克）.铜的重量：230 X2^3 = 12〔克）・新台金中锌的重量；36-12=24 （克）.新合金内铜和锌的比：12 : 24=1 : 2.答’新合金内铜和锌的比是1 : 2.例4师徒两人共加工零件1昭个.师博抑工一个零件用5分钟，徒弟加工一个零件用9分钟，完成任务时，两人各加工零件多少个？1分祈师博加工一个零件用盼钟，每分钟可加工扌个零件，徒弟加工一个零件用9分钟，每分钟可加工零件;个，师徒两人数率的比是二1& 59T作星由于两人的工作时间是一定的，根据口；專二工作吋间（一定），工作量与工作效率成正比例.解法h设师博加工x个，徒弟加工（163-.）个.1_ 5168-x 上9x 9168-x =55X=168X9-9K,14x = 168X9,x = 108.168-x=168-108^60 （个）*笥师傅加工10区个，徒弟加工60个.解法么由于师、徒两人工作效率的比是、右那么他们工作量的比也是、p因此师傅工作量是徒弟工作量的咼（倍），徒弟的工作量为1倍量”16旷（卜討1）= 168^ 2—5=60 （个），（徒弟）.60X y） = 108（个），（师傅）・解法*师傅每分钟抑工？个.徒弟每分钟加工扌个，用相遇问题思考方法可求岀两人各用了多少分钟.然后用师、徒每分钟各自的效率，分别乘以540就是各自加工零件的个数.1 1 141用+（三+ §）=16区+亦匸刃°〔分钟）.|x 540= 108 （个）、（师傅）|x 540= 60 C^）,（徒弟）.例5洗衣机厂计划20天生产洗衣机16Q0台，生产5天后由于改进技术，效率提高25%,完成计划还要多少天？分析这是一道比例应用题.工效和工时是变量，不变量是计划生产5天后剩下的台数.从工效看，有原来的数率1600-20=80台/天，又有提高后的效率80X〔1 + 25%） =10。

最新冀教版六年级数学上册第2单元比和比例教学设计及教学反思最新冀教版六年级数学上册第2单元比和比例教学设计及教学反思-第二单元比率和比例■教材分析本单元以学生学习除法的含义、分数的含义以及分数与除法之间的关系为基础。

主要内容包括：理解比率和比率的基本性质，求比率和简化比率，理解比率和比率的基本性质，解决按比例分配问题。

最后，本单元安排了一个综合应用——“测量旗杆高度”。

比和比例的知识是“数与代数”领域“正比例、反比例”的部分内容，具体标准内容有四条：1．在实际情境中理解什么是按比例分配，并能解决简单的问题。

2．通过具体问题认识正比例、反比例的量。

3．能根据给出的正比例关系的数据在有坐标系的方格纸上画图，并根据一个量的值来估计另一个量的值。

4.能够找出生活中正比例和负比例的例子。

“比率”表示两个数的除法之间的关系，即比率的前后项之间的关系足以表示除数和除数之间的关系。

任何两个相关数字之间的关系都可以抽象为两个数字的比率。

比例分配是指按一定比例分配数量。

它是比较知识在生产和生活中的具体应用。

本单元教材在编写思路、内容安排、教学方法等方面发生了很大变化，主要体现在以下几个方面：一、让学生在具体情境中学习数学，理解数学概念。

本单元要认识的数学概念有比、比例、按比例分配等，学生对这些概念实际意义的理解，是学生能否应用比的知识解决问题的关键。

所以，教材淡化概念“形式化”叙述，通过选取学生熟悉的、鲜活的事例，让学生在具体情境中理解比和比例及按比例分配的实际意义。

二、让学生体验知识的发生和发展，自主建构数学知识。

本文着重研究数学知识之间的联系，从学生已有的知识和经验出发，使学生会在利用已有知识独立运作的过程中，能够积极主动地构建知识体系。

三、注重解决实际问题，培养学生的应用意识。

本单元选取了大量的、真实的工农业生产和现实生活中的典型事例，并给学生自主解决问题的空间。

让学生在自主解决这些问题的实际问题中，体会比和比例知识在现实生活中应用的广泛性，培养学生应用数学知识解决实际问题的意识和能力，增强学好数学的自信心。