热学竞赛题(附解题过程)

高中物理竞赛——热学一．分子动理论1、物质是由大量分子组成的（注意分子体积和分子所占据空间的区别）对于分子（单原子分子）间距的计算，气体和液体可直接用3分子占据的空间，对固体，则与分子的空间排列（晶体的点阵）有关。

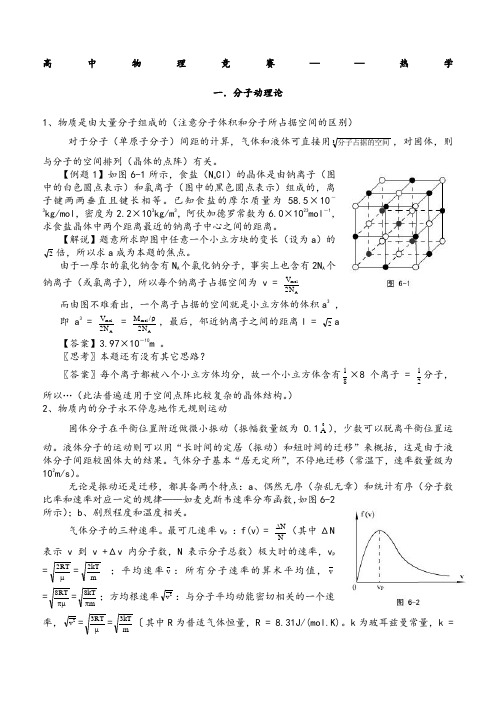
【例题1】如图6-1所示，食盐（N a Cl ）的晶体是由钠离子（图中的白色圆点表示）和氯离子（图中的黑色圆点表示）组成的，离子键两两垂直且键长相等。

已知食盐的摩尔质量为58.5×10－3kg/mol ，密度为2.2×103kg/m 3，阿伏加德罗常数为6.0×1023mol －1，求食盐晶体中两个距离最近的钠离子中心之间的距离。

【解说】题意所求即图中任意一个小立方块的变长（设为a ）的2倍，所以求a 成为本题的焦点。

由于一摩尔的氯化钠含有N A 个氯化钠分子，事实上也含有2N A 个钠离子（或氯离子），所以每个钠离子占据空间为 v =Am olN 2V而由图不难看出，一个离子占据的空间就是小立方体的体积a 3 ， 即 a 3 =Am ol N 2V = Am ol N 2/M ρ，最后，邻近钠离子之间的距离l =2a【答案】3.97×10－10m 。

〖思考〗本题还有没有其它思路？〖答案〗每个离子都被八个小立方体均分，故一个小立方体含有81×8个离子 = 21分子，所以…（此法普遍适用于空间点阵比较复杂的晶体结构。

） 2、物质内的分子永不停息地作无规则运动固体分子在平衡位置附近做微小振动（振幅数量级为0.1A 0），少数可以脱离平衡位置运动。

液体分子的运动则可以用“长时间的定居（振动）和短时间的迁移”来概括，这是由于液体分子间距较固体大的结果。

气体分子基本“居无定所”，不停地迁移（常温下，速率数量级为102m/s ）。

无论是振动还是迁移，都具备两个特点：a 、偶然无序（杂乱无章）和统计有序（分子数比率和速率对应一定的规律——如麦克斯韦速率分布函数，如图6-2所示）；b 、剧烈程度和温度相关。

高中物理竞赛——热学一．分子动理论1、物质是由大量分子组成的（注意分子体积和分子所占据空间的区别）对于分子（单原子分子）间距的计算，气体和液体可直接用3分子占据的空间，对固体，则与分子的空间排列（晶体的点阵）有关。

【例题1】如图6-1所示，食盐（N a Cl ）的晶体是由钠离子（图中的白色圆点表示）和氯离子（图中的黑色圆点表示）组成的，离子键两两垂直且键长相等。

已知食盐的摩尔质量为58.5×10－3kg/mol ，密度为2.2×103kg/m 3，阿伏加德罗常数为6.0×1023mol －1，求食盐晶体中两个距离最近的钠离子中心之间的距离。

【解说】题意所求即图中任意一个小立方块的变长（设为a ）的2倍，所以求a 成为本题的焦点。

由于一摩尔的氯化钠含有N A 个氯化钠分子，事实上也含有2N A 个钠离子（或氯离子），所以每个钠离子占据空间为 v =Am ol N 2V而由图不难看出，一个离子占据的空间就是小立方体的体积a 3 ， 即 a 3 =Am ol N 2V = Am ol N 2/M ρ，最后，邻近钠离子之间的距离l =2a【答案】3.97×10－10m 。

〖思考〗本题还有没有其它思路？〖答案〗每个离子都被八个小立方体均分，故一个小立方体含有81×8个离子 =21分子，所以…（此法普遍适用于空间点阵比较复杂的晶体结构。

）2、物质内的分子永不停息地作无规则运动固体分子在平衡位置附近做微小振动（振幅数量级为0.1A 0），少数可以脱离平衡位置运动。

液体分子的运动则可以用“长时间的定居（振动）和短时间的迁移”来概括，这是由于液体分子间距较固体大的结果。

气体分子基本“居无定所”，不停地迁移（常温下，速率数量级为102m/s ）。

无论是振动还是迁移，都具备两个特点：a 、偶然无序（杂乱无章）和统计有序（分子数比率和速率对应一定的规律——如麦克斯韦速率分布函数，如图6-2所示）；b 、剧烈程度和温度相关。

13、15、 CJT L ：初中科学竞赛经典测试2《热学》 评分标准、参考答案与思路解析一、选择题（每小题2分，共40分。

请选出各题中一个符合题意的选项）难题思路解析：9、A 、实验中，沙子吸热升温较快，说明沙子的比热容小，吸热能力弱，故A 错误.B 、 在本实验中，物体吸热多少是由加热时间决定的.故13错误.C 、 将沙子和水加热到相同温度时，据Q=cmAt,水吸收的热量多.故C 错误.D 、 加热相同的时间，吸收的热量相等，据Q=cmAt,末温低的物质比热容大，吸热能力强.故 D 正确. —具尸体半天时间大约的散热量:Q-=CmAt=4. 2X107/ （kg 弋）X60kgX （37匸-25匕） =3.024X107；正常人一天内的散热量:Q ；二Q ：十60%X 2=3.024X 10s J4-0.6X2=1.008X10 J m=ft/g=1.008X 10J/L.6X 10'j^0.63kg=630g.设热水和冷水的温度差为t ，•・•质量为恥的一小杯热水倒入盛有质量为m 的冷水的保温容器 中，使得冷水温度升高了 10C, ・・・QkQ 钦,、从而可知，cm ：（七-10匸）=cmX10*C, --------------------- ①a 又向保温容器中倒入一小杯同质量为m ：同温度的热水，水温又上升了 6T3,Q/=Q 农，从而可知'cm ： （） =c （m+in ：） X6X3, ----------------- ② 则①-②得：6*0 X cmplOf X cm-6*C X cm-6*C X emc ， 整理得：12*C X cmc=4*C X cm, 解得：m=3jn ：; 3 代入①式可得，“假设我们将全部热水一次性注入，则由热平衡方程可知: （40匸-/^七）=jncAt, m=3jnc ；卩联立两式解得：At=20*C> I 稽一则注入后3杯水后，水温还会上升：20lC-10r-6TC=4，C ・因为温度与时间不是线性关系，而八体现的是温度与时间是线性关系，故A 错误.在热传递 过程中两物体温度差越大热传递进行的越快，髙温物体温度下降的快，低温物体温度升漓的 越快•而B 选项中没体现这一点，故B 错误.C 选项中体现了温度高时热传递进行的慢，温 度低时进行的快，即温度高时温度变化的慢，温度低时温度变化的快.故C 错误.选项D 体 现出了在热传递过程中两物体温度差越大热传递进行的越快，高温物体温度下降的快，低温 物体温度升高的越快.两物体温度差越小热传递进行的越慢，高温物体温度下降的慢，低温即:C甲20匸C水m水801C- t0同理则有:C乙葺20匸C水m水601C- t0物体温度升高的也慢.最终温度在50°C左右.所以D正确.17、设发热功率均为P,贝9：A： k (AtA-AtB)二P,即A的散热功率等于发热功率.B： k (AtB-AtC)二P+k (AtA-AtB),即B的散热功率等于自身的发热功率与A的散热功率之和.C： k (AtC) =P+k (AtB-AtC),即C的散热功率等于自身的发热功率与13的散热功率之和. 整理得：AtA=2A tC3AtB=5AtC即得：AtA： AtB： AtC=6： 5： 318、设热水原来的溟度热水和质量JTI冰水混合后的盘度为t；＞且3・・•不计热量损失，纟己垄. '汀汀月I / /^ “/.Q y=Q 毁，"/ 3则第一次，质量为m、温度为Of的雪与质量为M的热水混合后，d cM (=cm (t；-0) 3即：Mt=mt；一① I / {If A第二次质量为2m、温度为OC的雪与质量为(畑)的热水混合后ac (M+m) t=cX 2m[ (t；-t) P]即：Mt+3]Rt=2mt2 ---------- ②由①②解得：M=3m A ・即m： M=l： 3. —• CfJ | f19、中年人漫步行走时，每秒钟体內产生的热量为35焦，即其总功率是P=W/t=35j/lS=35W故此时出汗的散热功率为W：=35W-33W=2W；故该人在行走lh时汗的散热量为W=Pt=2WX36OOs=72OOJ,由于每蒸发18克汗水所需要的能量为4300焦，故此时人所需的出汗壘是m=7200j/4300J X 18g^30g20、设冷水的温度为to,甲投入冷水后放热Q放二C甲m (100°C - 20°C - to),水吸H攵的热量为Q吸二C水m水20°C, 21世纪教育网版权所有•・•不考虑热传递过程热量的损失，则有Q沪Q毁，・・・C 甲m (100°C - 20°C - to)二C 水m 水20°C,乙投入冷水后放热Q放'=C乙m (100°C・20°C・20°C・to), 水吸收的热量仍为Q吸二C水m水20°C,第二种方式：设乙投入冷水热平衡后，水温为t|,甲投入冷水热平衡后的水温为t2,则有:C 乙m (100°C - ti)二C 水m 水(ti - to),T 质量为JTL ：的一小杯热水倒入2有质量为m 的冷水的保温容器中，使得冷水温度升高了 5C,职語蕊先 -----C 甲 m ( 100 C - t2)二C 水 m 水(t2 - t 】)， • c 水ID 水 ioo1C- t 2综合①②③④式，解得t 2 - to=4O°C 二、简答题(每空2分，共52分) 21、 (1)材料 1(2) 20°0(3)第 35 分钟 T1 中的 5022、 (1)空气热胀冷缩 (2)降低 下端 (3)受大气压变化的影响 23、 (1)乙 乙(2) 2. 4X103 24、 小于大于25、 小红的想法更合理。

重点高中物理竞赛热学高中物理竞赛——热学一．分子动理论1、物质是由大量分子组成的（注意分子体积和分子所占据空间的区别）对于分子（单原子分子）间距的计算，气体和液体可直接用3分子占据的空间，对固体，则与分子的空间排列（晶体的点阵）有关。

【例题1】如图6-1所示，食盐（N a Cl ）的晶体是由钠离子（图中的白色圆点表示）和氯离子（图中的黑色圆点表示）组成的，离子键两两垂直且键长相等。

已知食盐的摩尔质量为58.5×10－3 kg/mol ，密度为 2.2×103kg/m 3，阿伏加德罗常数为6.0×1023mol －1，求食盐晶体中两个距离最近的钠离子中心之间的距离。

【解说】题意所求即图中任意一个小立方块的变长（设为a ）的2倍，所以求a 成为本题的焦点。

由于一摩尔的氯化钠含有N A 个氯化钠分子，事实上也含有2N A 个钠离子（或氯离子），所以每个钠离子占据空间为v=Am olN 2V而由图不难看出，一个离子占据的空间就是小立方体的体积a 3，即a 3=Am ol N 2V =Am ol N 2/M ρ，最后，邻近钠离子之间的距离l=2a【答案】3.97×10－10m 。

〖思考〗本题还有没有其它思路？〖答案〗每个离子都被八个小立方体均分，故一个小立方体含有8 1×8个离子=21分子，所以…（此法普遍适用于空间点阵比较复杂的晶体结构。

） 2、物质内的分子永不停息地作无规则运动固体分子在平衡位置附近做微小振动（振幅数量级为0.1A 0），少数可以脱离平衡位置运动。

液体分子的运动则可以用“长时间的定居（振动）和短时间的迁移”来概括，这是由于液体分子间距较固体大的结果。

气体分子基本“居无定所”，不停地迁移（常温下，速率数量级为102m/s ）。

无论是振动还是迁移，都具备两个特点：a 、偶然无序（杂乱无章）和统计有序（分子数比率和速率对应一定的规律——如麦克斯韦速率分布函数，如图6-2气体分子的三种速率。

全国中学生物理竞赛集锦（热学）第21届预赛2004.9.5 一、（15分）填空e ．在标准状态下，1cm 3 气体中的分子数约为____________。

（阿伏加德罗常量 N A ＝6.02×1023 mol －1） 第21届复赛一、(20分)薄膜材料气密性能的优劣常用其透气系数来加以评判．对于均匀薄膜材料，在一定温度下，某种气体通过薄膜渗透过的气体分子数，其中t 为渗透持续时间，S 为薄膜的面积，d 为薄膜的厚度，为薄膜两侧气体的压强差．k 称为该薄膜材料在该温度下对该气体的透气系数．透气系数愈小，材料的气密性能愈好．图为测定薄膜材料对空气的透气系数的一种实验装置示意图．EFGI 为渗透室，U 形管左管上端与渗透室相通，右管上端封闭；U 形管内横截面积A ＝0.150cm 2．实验中，首先测得薄膜的厚度d =0.66mm ，再将薄膜固定于图中处，从而把渗透室分为上下两部分，上面部分的容积，下面部分连同U 形管左管水面以上部分的总容积为V 1，薄膜能够透气的面积S =1.00cm 2．打开开关K 1、K 2与大气相通，大气的压强P 1＝1.00atm ，此时U 形管右管中气柱长度，．关闭K1、K 2后，打开开关K 3，对渗透室上部分迅速充气至气体压强，关闭K 3并开始计时．两小时后， U 形管左管中的水面高度下降了．实验过程中，始终保持温度为．求该薄膜材料在时对空气的透气系数．（本实验中由于薄膜两侧的压强差在实验过程中不能保持恒定，在压强差变化不太大的情况下，可用计时开始时的压强差和计时结束时的压强差的平均值来代替公式中的．普适气体常量R = 8.31Jmol-1K-1，1.00atm = 1.013×105Pa）．第20届预赛三、(20分)在野外施工中，需要使质量 m＝4.20 kg的铝合金构件升温。

除了保温瓶中尚存有温度t＝90.0℃的1.200 kg的热水外，无其他热源．试提出一个操作方案，能利用这些热水使构件从温度 t0=10℃升温到66.0℃以上（含66.0℃），并通过计算验证你的方案．已知铝合金的比热容 c＝0.880×l03J·(Kg·℃)-1，水的比热容c0=4.20×103J·(Kg·℃)-1，不计向周围环境散失的热量。

[题1]一大杯冷水的温度为t1，一小杯热水的温度为t2，将它们混合后的温度为t，下列四个关系式中，正确的是()A、B、C、D、特殊值法解：根据题意，可令冰水质量m1=3千克，温度t1=2℃，热水质量m2=1千克，t2=10℃，根据Q吸=Q放，cm1(t-t1)=cm2(t2-t)，代入数据解得：t=4℃，=6℃，所以t＜，选C。

评析：特殊值法是一种重要的解题方法，有一些比较物理量大小类习题，根据题意取特殊值可把复杂的代数运算变为简洁的数字运算，从而能够迅速得出答案。

[题2] 两个质量相同的铜球温度都为t1，把它们分别放入质量相同初温都为t2的水和酒精中，已知t1＞t2，忽然热量损失，则达到热平衡后，的末温高。

极限法解：根据C水＞C酒，C水大些，就让C水趋于无穷大，根据比热大的物体难冷难热，铜球放入后，水的温度基本不变，末温为t2；C酒小些，就让C酒趋于无穷小，根据比热小的物体易冷易热，铜放入后，酒精的温度由t2变为t1，根据t1＞t2，酒精的末温高些。

评析：极限法实质也是特殊值法，比较物理量大小类习题，让大的个量取无穷大，(或某个临界值)，小的个量取无穷小(或某个临界值)，则更能迅速得出答案，使解题更具创意。

[例3] 甲、乙两个杯子装有质量相同，温度不同的同种液体。

取甲杯中的一半液体倒入乙杯，达到热平衡后再取乙杯中的一半液体倒入甲杯，已知甲杯液体初温为20℃，最后温度为30℃，求乙杯中液体的初温是多少？(在倒的过程中没有与外界发生热交换) 作法法解：将甲杯液体一半倒入乙杯后如图1,将乙杯液体一半倒入甲杯后如图2，以图2甲杯内液体为研究对象，杯中有的甲液体，有的乙液体，根据Q甲吸=Q乙放，得：cm甲(30℃-20℃)=cm乙(t0乙-30℃)解得t0乙=45℃。

评析：同学们通过审题在头脑中形成的物理图景是模糊的，闪烁不定的，通过作图，物理图景变得清晰稳定，如本题通过作图就清晰的展示了甲杯中原来的液体是多少，乙杯又向甲杯倒入原来的液体是多少，从而解决了问题。

高中物理竞赛——热学一．分子动理论1、物质是由大量分子组成的注意分子体积和分子所占据空间的区别对于分子单原子分子间距的计算;气体和液体可直接用3分子占据的空间;对固体;则与分子的空间排列晶体的点阵有关..例题1如图6-1所示;食盐N a Cl 的晶体是由钠离子图中的白色圆点表示和氯离子图中的黑色圆点表示组成的;离子键两两垂直且键长相等..已知食盐的摩尔质量为58.5×10－3kg/mol;密度为 2.2×103kg/m 3;阿伏加德罗常数为 6.0×1023mol －1;求食盐晶体中两个距离最近的钠离子中心之间的距离..解说题意所求即图中任意一个小立方块的变长设为a 的2倍;所以求a 成为本题的焦点..由于一摩尔的氯化钠含有N A 个氯化钠分子;事实上也含有2N A 个钠离子或氯离子;所以每个钠离子占据空间为 v =Am ol N 2V而由图不难看出;一个离子占据的空间就是小立方体的体积a 3 ; 即 a 3 =Am ol N 2V = Am ol N 2/M ρ;最后;邻近钠离子之间的距离l =2a答案3.97×10－10m ..〖思考〗本题还有没有其它思路〖答案〗每个离子都被八个小立方体均分;故一个小立方体含有81×8个离子 = 21分子;所以…此法普遍适用于空间点阵比较复杂的晶体结构.. 2、物质内的分子永不停息地作无规则运动固体分子在平衡位置附近做微小振动振幅数量级为0.1A 0;少数可以脱离平衡位置运动..液体分子的运动则可以用“长时间的定居振动和短时间的迁移”来概括;这是由于液体分子间距较固体大的结果..气体分子基本“居无定所”;不停地迁移常温下;速率数量级为102m/s..无论是振动还是迁移;都具备两个特点：a 、偶然无序杂乱无章和统计有序分子数比率和速率对应一定的规律——如麦克斯韦速率分布函数;如图6-2所示；b 、剧烈程度和温度相关..气体分子的三种速率..最可几速率v P ：fv = NN ∆其中ΔN 表示v 到v +Δv 内分子数;N 表示分子总数极大时的速率;v P =μRT 2=m kT 2 ；平均速率v ：所有分子速率的算术平均值;v=πμRT 8=m kT 8π；方均根速率2v ：与分子平均动能密切相关的一个速率;2v =μRT 3=mkT 3〔其中R 为普适气体恒量;R = 8.31J/mol.K..k 为玻耳兹曼常量;k = AN R =1.38×10－23J/K 〕例题2证明理想气体的压强P = 32n K ε;其中n 为分子数密度;K ε为气体分子平均动能..证明气体的压强即单位面积容器壁所承受的分子的撞击力;这里可以设理想气体被封闭在一个边长为a 的立方体容器中;如图6-3所示..考查yoz 平面的一个容器壁;P =2a F ①设想在Δt 时间内;有N x 个分子设质量为m 沿x 方向以恒定的速率v x 碰撞该容器壁;且碰后原速率弹回;则根据动量定理;容器壁承受的压力F =tp ∆∆=tmv 2N x x ∆• ②在气体的实际状况中;如何寻求N x 和v x 呢考查某一个分子的运动;设它的速度为v ;它沿x 、y 、z 三个方向分解后;满足 v 2 = 2x v + 2y v + 2z v分子运动虽然是杂乱无章的;但仍具有“偶然无序和统计有序”的规律;即2v = 2xv + 2y v + 2z v = 32x v ③这就解决了v x 的问题..另外;从速度的分解不难理解;每一个分子都有机会均等的碰撞3个容器壁的可能..设Δt =xv a;则N x = 61·3N 总 = 21na 3 ④注意;这里的61是指有6个容器壁需要碰撞;而它们被碰的几率是均等的..结合①②③④式不难证明题设结论.. 〖思考〗此题有没有更简便的处理方法〖答案〗有..“命令”所有分子以相同的速率v 沿+x 、 x 、+y 、 y 、+z 、 z 这6个方向运动这样造成的宏观效果和“杂乱无章”地运动时是一样的;则 N x =61N 总 = 61na 3 ；而且v x = v所以;P =2a F = 2xx at mv 2N •∆•=2xx 3a v amv 2na 61••=31nm 2x v = 32n K ε3、分子间存在相互作用力注意分子斥力和气体分子碰撞作用力的区别;而且引力和斥力同时存在;宏观上感受到的是其合效果..分子力是保守力;分子间距改变时;分子力做的功可以用分子势能的变化表示;分子势能E P 随分子间距的变化关系如图6-4所示..分子势能和动能的总和称为物体的内能.. 二、内能1．物体的内能1自由度i ：即确定一个物体的位置所需要的独立坐标系数..如自由运动的质点;需要用三个独立坐标来描述其运动;故它有三个自由度.. 2物体的势能3物体中所有分子热运动的动能和分子势能的总和称为物体的内能.. 2．理想气体的内能P OVBA D C 理想气体的分子之间没有相互作用;不存在分子势能..因此理想气体的内能是气体所有分子热运动动能的总和;它只跟气体的分子数和温度有关;与体积无关.. 分子热运动的平均动能：理想气体的内能可以表达为：注意：N/NA=m/M=n;R=NAk ；对于单原子分子气体i=3;对于双原子分子气体i=5.. 一定质量的理想气体的内能改变量：二、改变内能的两种方式 1．做功和传热2．功的计算1机械功 2流体体积变化所做的功 气体对外界所作的元功：ΔW｜=pSΔx=pΔV ..外界活塞对气体做元功：ΔW=-ΔW ｜=-pΔV ；总功W=∑ΔWi=-∑piΔVi ..当气体膨胀时ΔV＞0;外界对气体做功W ＜0；气体压缩时ΔV＜0;外界对气体做功W ＞0..准静态过程可用p-V 图上一条曲线来表示;功值W 为p-V 图中过程曲线下的面积;当气体被压缩时W ＞0;反之W ＜0.. 3.热传递内能从一个物体转移到另一个物体;或者从物体的一部分转移到同一物体的邻近部分的过程叫热传递..热传递的方式有三种：对流、传导和辐射 1对流 2热传导※如果导热体各点温度不随时间变化;这种导热过程称为稳定导热;在这种情况下;考虑长度为l;横截面积为S 的柱体;两端截面处的温度为T1;T2且T1>T2;则热量沿着柱体长度方向传递;在△t 时间内通过横截面S 所传递的热量为：式中K 为物质的导热系数..固体、液体和气体都可以热传导;其中金属的导热性最好;液体除水银和熔化的金属外;导热性不好;气体的导热性比液体更差..石棉的热传导性能极差;因此常作为绝热材料.. 3热辐射一切物体都发射并吸收电磁波..物体发射电磁波又称热辐射;发射出的是不同波长的电磁波..温度越高;辐射的能量越多;辐射中短波成份比例越大..一定时间内物体辐射能量的多少以及辐射能量按波长的分布都与物体的温度有关;这种与温度有关的辐射称为热辐射.. 热辐射在真空环境中也能进行；热辐射与周围物体的温度高低是无关的.. 三、热力学第一定律 1．热力学第一定律 2．热量的计算 热容质量为m 、比热为c 的系统在一个热力学过程中;升高或降低温度为△T;则该系统吸收或放出的热量为：定义热容：n c cm C n ==;式中cn 为摩尔热容;n 为摩尔数.. 结合热力学第一定律;可得： ※3．气体的自由膨胀四、热力学第一定律对理想气体热力学过程的应用 1．理想气体的等容过程恒量=T p; 0=∆=V p -W ..式中：R 2i T E T Q C V ⋅=∆∆=⎪⎭⎫⎝⎛∆=定容条件;又称之为定容摩尔热容.. 2．理想气体的等压过程恒量=T V;T -nR V p -W ∆=∆=;Q=nCp ΔT;定压摩尔热容量Cp 与定容摩尔热容量Cv 的关系有Cp=Cv+R=R i 22+..3．理想气体的等温过程pV=恒量;△E=0;Q=-W..在等温膨胀过程中;体积从V1变为V2;吸热为：12V Vln nRT = Q在等温压缩过程中;体积从V1变为V2;放热为：21V Vln nRT = Q4．理想气体的绝热过程气体始终不与外界交换热量的过程称之为绝热过程;即Q=0..恒量=T pV..绝热过程的状态方程是：γγ2211V p V p =或1-221-11V T V T γγ=其中：i i R i R i C C V p 2222+=+==γ 5．其他过程气态方程： nRT pV =热力学第一定律： △E=W+Q=nCV △T功：p-V 图中过程曲线下面积;要注意功的正负..过程方程：由过程曲线的几何关系找出过程的p ～V 关系式.. ※五、热力第二定律 1．循环过程 热机物质系统由某一状态出发;经历一系列的变化过程又回到初始状态;这样的周而复始的变化过程为循环过程;简称循环..在p-V 图上;物质系统的循环过程用一个闭合的曲线表示..经历一个循环;回到初始状态时;内能不变;因此△E=0..利用物质系统称为工作物质持续不断地把热转换为功的装置叫做热机..热机循环过程在P-V 图上是一根顺时针绕向的闭合曲线热机效率表示吸收来的热量有多少转化为有用的功;是热机性能的重要标志之一;效率的定义为：＜11121Q Q -Q W /==η获得低温装置的致冷机也是利用工作物质的循环过程来工作的;不过它的运行方向与热机中工作物的循环过程相反.. 2．卡诺循环卡诺循环是在两个温度恒定的热源之间工作的循环过程.. 卡诺热机的效率为：致冷机的功效常用从低温热源中吸热Q2和所消耗的外功W 的比值来量度;称为致冷系数;即：..3．热力学第二定律违背热力学第一定律的过程都不可能发生;不违背热力学第一定律的过程不一定都可以发生.. 自然过程是按一定方向进行的..表述1：不可能制成一种循环动作的热机;只从一个热源吸取热量;使之全部变为有用的功;而其他物体不发生任何变化..表述2：不可能将热量从低温物体传到高温物体而不引起其它变化即热量不会自动地从低温物体传到高温物体在表述1中;我们要特别注意“循环动作”几个字;如果工作物进行的不是循环过程;如气体作等温膨胀;那么气体只使一个热源冷却作功而不放出热量便是可能的.. 表述1与表述2具有等价性;是相互依存的.. 4．卡诺定理卡诺循环中每个过程都是平衡过程;所以卡诺循环是理想的可逆循环.. 卡诺定理指出：1在同样高温温度为T1和低温温度为T2之间工作的一切可逆机;不论用什么工作物;效率都等于）（12T T -1.. 2在同样高低温度热源之间工作的一切不可逆机的效率;不可能高于可逆机;即：）（12T T -1≤η..5．热力学第二定律的统计意义 内能、热力学定律典型例题例1 一箱理想气体;由N 个分子组成;用mi 表示第i 个分子的质量;vi 表示第i 个分子的相对箱子无规则运动的速度;i=1;2;…;N ．若整箱气体又以恒定的速度u 运动;求此箱气体的总动能和内能．例2质量为m1的圆筒水平地放置在真空中;质量为m2、厚度可忽略的活塞将圆筒分为体积相同的两部分;如图所示..圆筒的封闭部分充有n 摩尔的单原子理想气体氦;气体的摩尔质量为M;温度为T0;突然放开活塞;气体逸出..试问圆筒的最后速度是多少 设摩擦力、圆筒和活塞的热交换以及气体重心的运动均忽略不计..T0=273K;m1=0.6kg;m2=0.3kg;n=25mol;氦的摩尔质量为M ＝4×10-3kg/mol;cV=12.6J/mol ·K;γ=5/3例3横截面积为S 和αSα＞1;长度相同的两圆柱形“对接”的容器内盛有理想气体;每个圆筒中间位置有一个用硬杆相连的活Ⅰ Ⅱ Ⅲ塞;如图所示..这时舱Ⅰ内气体压强为p1;舱Ⅲ内气体压强为βp1;活塞处于平衡;整个系统吸收热量Q;温度上升;使各舱温度相同..试求舱Ⅰ内压强的变化..1mol 气体内能为CTC 是气体摩尔热容量;圆筒和活塞的热容量很小;摩擦不计..例4将1mol 温度为27℃的氦气;以100m/s 的定向速度注入体积为15L 的真空容器中;容器四周绝热..求平衡后的气体压强..例5绝热容器A 经一阀门与另一容积比A 的容积大得多的绝热容器B 相连..开始时阀门关闭;两容器中盛有同种理想气体;温度均为30℃;B 中气体的压强是A 中的两倍..现将阀门缓慢打开;直至压强相等时关闭..问此时容器A 中气体的温度为多少 假设在打开到关闭阀门的过程中处在A 中的气体与处在B 中的气体之间无热交换..已知每摩尔该气体的内能为E=2.5RT..例6一根长为76cm 的玻璃管;上端封闭;插入水银中..水银充满管子的一部分..封闭体积内有空气1.0×10-3mol;如图所示;大气压为76cmHg..空气的定容摩尔热容量CV=20.5J ·mol-1·K-1;当玻璃管温度降低10℃时;求封闭管内空气损失的热量..例7一台四冲程内燃机的压缩比r=9.5;热机抽出的空气和气体燃料的温度为27℃;在latm=105Pa 压强下的体积为9.5V0;如图所示;从1→2是绝热压缩过程；2→3混合气体燃爆;压强加倍；从3→4活塞外推;气体绝热膨胀至体积9.5V0;这时排气阀门打开;压强回到初始值latm 压缩比是气缸最大与最小体积比;γ是比热容比..求：1确定状态1、2、3、4的压强和温度；2求此循环的热机效率.. 例8有一卡诺致冷机;从温度为-10℃的冷藏室吸取热量;而向温度为20℃的物体放出热量..设该致冷机所耗功率为15kW;问每分钟从冷藏室吸取的热量是多少例9某空调器按可逆卡诺循环运转;其中的作功装置连续工作时所提供的功率P0..1夏天室外温度恒为T1;启动空调器连续工作;最后可将室温降至恒定的T2..室外通过热传导在单位时间内向室内传输的热量正比于T1-T2牛顿冷却定律;比例系数A..试用T1;P0和A 来表示T22当室外温度为30℃时;若这台空调只有30%的时间处于工作状态;室温可维持在20℃..试问室外温度最高为多少时;用此空调器仍可使室温维持在20℃..3冬天;可将空调器吸热、放热反向..试问室外温度最低为多少时;用此空调器可使室温维持在20℃..00。

1. 理想气体的压强，温度的微观解释2. 理想气体的内能3. 热力学第一定律知识点拨一．理想气体的微观模型先来作个估算：在标准状态下，1mol 气体体积1330104.22--⨯=moI m V ，分子数1231002.6-⨯=moI N A ，若分子直径m d 10100.2-⨯=，则分子间的平均间距m N V L A 93/101034.3)/(-⨯==，相邻分子间的平均间距与分子直径相比17/≈d L 。

由此可知：气体分子间的距离比较大，在处理某些问题时，可以把气体分子视为没有大小的质点；同时可以认为气体分子除了相互碰撞或者跟器壁碰撞之外，分子力也忽略不计，分子在空间自由移动，也没有分子势能。

因此理想气体是指分子间没有相互作用和分子可以看作质点的气体。

这一微观模型与气体愈稀薄愈接近于理想气体的宏观概念是一致的。

1．理想气体的压强宏观上测量的气体施给容器壁的压强，是大量气体分子对器壁不断碰撞的结果。

在通常情况下，气体每秒碰撞21cm 的器壁的分子数可达2310。

在数值上，气体的压强等于单位时间内大量分子施给单位面积器壁的平均冲量。

可以用动量定理推导，其表达式为K n P ε32=设气体分子都以平均速率v 运动，因沿上下、左右、前后各向运动的机会均等，所以各占总数的16．若分子的数密度（即单位体积内气体的分子数）为n ，则单位时间内碰撞单位面积器壁的分子数应为1(1)6n v ×．每个分子每次与器壁碰撞时将施于器壁2mv 的冲量，所以压强211(1)263p n v mv nmv ==××，假设每个分子的速率相同．每个分子的平均平动动能2k 1ε2mv =，所以2k 12ε33p nmv n ==．，式中n 是单位体积内分子个数，221υεm K=是分子的平均平动动能，n 和K ε增大，意味着单位时间内碰撞单位面积器壁的分子数增多，分子碰撞器壁一次给予器壁的平均冲量增大，因而气体的压强增加。