截面法求内力

浅探内力分析之截面法摘要: 材料力学离不开内力分析，截面法更是求内力的一般方法，在展开工程设计时，如果建筑的受力分析准确性得不到保障，那么建筑的安全性和耐久性等就会出现问题。

本文从截面法对不同种内力的具体应用进行初步研究寻找其计算方法。

关键词: 材料力学；内力；截面法引言在工程设计过程中会运用许多的理论力学知识，截面法便是其中至关重要的一种，且短时间内难以被取代，因此截面法受到广泛运用。

本文即从截面法对不同种内力的具体应用题展开计算分析。

1 截面法1.1 截面法的定义截面法：用截面假想地把构件分成两部分，以此来分析明确内力大小，并以平衡条件确定其合力的方法。

1.2 截面法的研究对象内力：物体在受到外力作用而变形时,其内部各质点间的相对位置将发生变化。

相应地,各质点间的相互作用力也将发生改变。

这种由外力作用而引起的质点间相互作用力的改变量,即为材料力学中所研究的内力。

1.3 截面法的步骤主要分以下三个步骤：1、截开：在需要求内力的截面处，假想地将杆分为两部分；2、代替：将两部分中的任意一部分留下，把弃去部分对留下部分的作用，以作用在截面上的内力（力或力偶）代替；3、平衡：对留下部分建立平衡方程，根据上面的已知外力来计算杆件在截开面上的未知内力。

注意，截开面上的内力对留下部分而言已属外力。

图 12 轴力与杆件轴线相重合的内力，称为轴力，用符号FN表示。

轴力的正负规定: 当轴力的指向离开截面时,杆受拉,规定轴力为正;反之,当轴力指向截面时,杆受压,规定轴力为负。

即拉为正,压为负。

2.1 轴力分析计算已知F1=4OKN，F2=-30KN，求AB杆的内力。

应用截面法求杆件横截面上的内力，如图2所示。

截开：用假想平面m-m将构件切开分为两部分。

代替：取出其中任一部分如I部分为研究对象,画出I部分的受力图平衡：列出Ⅰ部分的平衡方程式:由∑Fx=0，得Fx-F=0，得FN=F1=4OKN（背离横截面,拉力为正）求BC杆的内力。

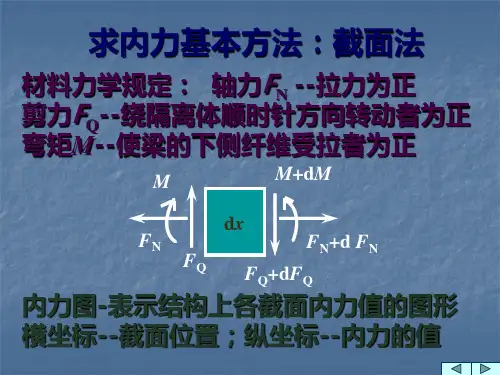
截面法‹1截面法可以快速求出某一内力，通常取结构 的一部分为隔离体，其上力系为平面一般力系。

每个隔离体上有3个独立平衡方程。

一般表示 为： ∑ FX = 0 投影法 ∑ FY = 0 力矩法 ∑M = 0 计算要点： 尽量使一个方程解一个未知数，避免求解 联立方程。

一. 力矩法例：求图示桁架1、2、3杆的轴力。

2VAVB解：由整体平衡条件求得支座反力 VA=VB HA=0作Ⅰ--Ⅰ截面,截开1、2、3杆的轴力 取截面以左为隔离体。

Ⅰ3Ⅰ（1）求1杆轴力N1K14选取未知力N2和N3 延长线的交点K1作 为取矩点。

N1 对K1点取矩，由 ∑MK1 = 0 从而求出所求未知 力N1。

VA（2）求2杆轴力N2N2 K2 VAY252X2由∑MK2 = 0 ,比例关系从而求出所求未知力Y2。

2杆轴力N2（3）求3杆轴力N3Y3 N3 X3K3 VA6由 ∑MK3 = 0比例关系从而求出所求未知力X3。

3杆轴力N3力矩法要点：„7„„欲求某指定杆内力，则作一截面，截开待求 杆； 隔离体上除所求未知力外，其余未知力的延 长线均交于某一点K。

对K点取矩，从而求出所求未知力 。

（1）选择其余未知力延长线的交点K作为取矩 点，从而用∑MK=0，求出指定杆内力。

（2）将斜杆的内力放在某一个合适的点上分 解，使其一个分力通过取矩点K。

例1. 求图示桁架杆件a、b、c的轴力890kN30kN作Ⅰ—Ⅰ截面Ⅰ9Ⅰ求NaNa 求Na时，对另 外两个未知力的 交点C取矩，10C由 ΣMc＝0，得 Na×4＋30×8＝030kN解得： Na =－ 60kN求NbD Xb E Yb Nb30kN11求Nb时，对点D取矩。

将Nb 其在E点处分解 为水平和竖向分量。

由ΣMD＝0，得 Yb×12＋40×4 － 30×12＝0 解得 Yb＝16.67 kN由比例关系得到：N b = 2Yb = 2 × 16.67 = 23.57kN求NcYc XcD Nc12求Nc时，对点E取矩。

简述截面法求内力的过程
截面法是一种静力学方法，用于计算和分析结构中各个截面的内力。

其具体求解过程如下：
（1）根据结构的载荷情况和几何形状，选取一个截面。

（2）将该截面割开，同时保留截面两侧的支反力和弯矩。

（3）根据平衡条件和材料力学原理，分别求解在两侧支反力和弯矩的作用下，该截面两侧的内力分布。

（4）将所求的内力分布和所割开的截面形状结合起来，得到该截面中各点的内力大小和方向。

（5）重复上述过程，依次计算得到结构中各个截面的内力分布。

通过截面法求得的内力可以用于评估结构的受力性能、确定结构设计的可行性，以及优化结构的设计方案。

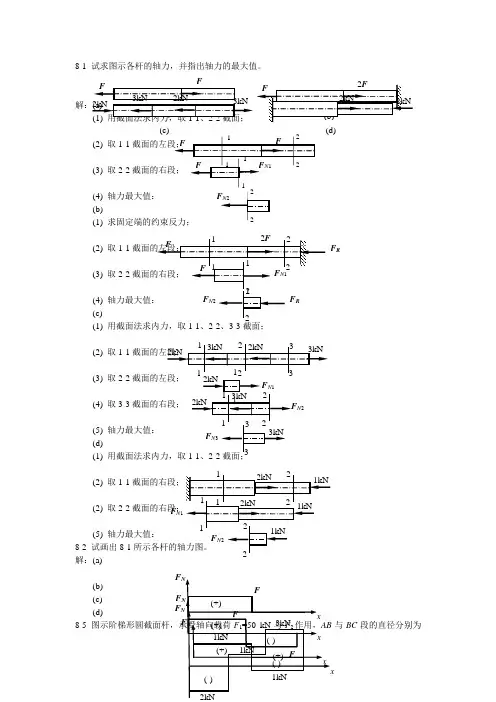
8-1 试求图示各杆的轴力，并指出轴力的最大值。

(2) 取1-1(3) 取2-2(4) 轴力最大值： (b)(1) 求固定端的约束反力； (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段；(5) 轴力最大值： (d)(1) 用截面法求内力，取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值： 8-2 试画出8-1解：(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。

解：(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求BC 段的直径。

解：(1)用截面法求出1-1、2-2截面的轴力；(2) 求1-1、2-2截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷F =10 kN 作用，杆的横截面面积A =1000 mm 2，粘接面的方位角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。

解：(1) (2) 8-14 2=20 mm ，两杆F =80 kN 作用，试校核桁架的强度。

解：(1) 对节点A(2) 列平衡方程 解得： (2) 8-15 图示桁架，杆1A 处承受铅直方向的载荷F 作用，F =50 kN ，钢的许用应力[σS ] =160 MPa ，木的许用应力[σW ] =10 MPa 。

解：(1) 对节点A (2) 84 mm 。

8-16 题8-14解：(1) 由8-14得到的关系；(2) 取[F ]=97.1 kN 。

8-18 图示阶梯形杆A 2=100 mm 2，E =200GPa ，试计算杆AC 的轴向变形 解：(1) (2) AC 8-22 图示桁架，杆1与杆2的横截面面积与材料均相同，在节点A 处承受载荷F 作用。

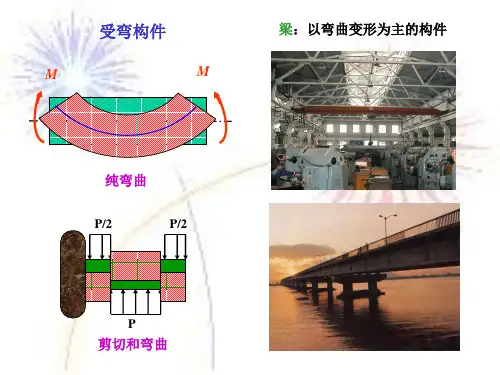
求杆件内力的基本方法
在工程学中，杆件内力是指作用在杆件内部的力，它是杆件受力状态的重要参数。

求解杆件内力是工程设计和结构分析的基本任务之一。

下面将介绍几种常用的求解杆件内力的基本方法。

1. 静力平衡法：静力平衡法是最基本的求解杆件内力的方法。

根据静力平衡条件，可以通过分析杆件受力平衡的方程来求解杆件内力。

静力平衡法适用于简单的静力系统，可以方便地得到杆件内力分布。

2. 截面法：截面法是一种基于截面平衡原理的求解杆件内力的方法。

根据杆件的几何形状和材料特性，可以通过分析截面上的受力平衡条件来求解杆件内力。

截面法适用于复杂的杆件结构，可以有效地得到杆件内力分布。

3. 外力法：外力法是一种基于外力作用的求解杆件内力的方法。

通过将外力作用在杆件上，可以根据受力平衡条件和变形关系求解杆件内力。

外力法适用于存在复杂荷载和约束条件的杆件结构，可以比较准确地得到杆件内力分布。

4. 能量方法：能量方法是一种基于能量原理的求解杆件内力的方法。

通过构建杆件的势能和应变能的表达式，可以利用最小势能原理或最小应变能原理求解杆件内力。

能量方法适用于需要考虑材料非线性和大变形的杆件结构，可以较为精确地得到杆件内力分布。

需要注意的是，不同的方法适用于不同的杆件结构和受力条件。

在实际应用中，应根据具体情况选择合适的方法来求解杆件内力，并结合实际工程要求进行验证和修正。

此外，随着计算机技术的不断发展，有限元分析等数值方法也成为求解杆件内力的重要工具之一。