基于分形几何的分形图绘制与分析
- 格式:doc
- 大小:26.50 KB
- 文档页数:6

分形几何学和分形分析的基础原理分形几何学是对自然界和人类活动中普遍存在的复杂结构进行研究的一门学科。
分形几何学的基础原理是分形性质的存在和分形维度的概念。
分形性质指的是在尺度变化下具有自相似性,即物体的部分结构与整体结构相似。
而分形维度则是用来描述分形物体复杂度的度量。
分形几何学的基本概念是由波尔曼德布罗特于20世纪70年代提出的。
他通过研究自然界中的山脉、云彩等不规则结构发现,这些结构在不同尺度下都具有相似的形态,即它们是自相似的。
波尔曼德布罗特认为,真实世界中的许多物体与几何学假设中的理想物体并不相符,而是存在着分形结构。
这一发现引发了对于自然界中不规则结构的深入研究,并为分形几何学的发展提供了基础。
分形几何学的另一个重要概念是分形维度。
传统几何学中的维度概念只适用于整数维空间中的几何体,如一维线段、二维平面和三维立体等。
然而,分形物体的形态复杂,无法用传统几何学中的维度来描述。
因此,分形几何学引入了分形维度的概念。
分形维度可以用于衡量分形物体的复杂程度,即其填充空间的能力。
分形维度的计算方法有多种,其中最常用的是盒维度和信息维度。
除了分形几何学,分形分析也是对分形性质的研究和应用。
分形分析是对数据序列或图像进行分形测度和特征提取的一种方法。
分形分析可以应用于多个领域,如信号处理、图像压缩、金融市场预测等。
分形分析的基础原理是将数据序列或图像看作是分形物体,利用分形维度等数学工具来描述和分析数据的局部和整体特征。
分形分析的一个重要应用是在信号处理领域中。
信号通常是由连续或离散的数据点组成的。
传统的信号处理方法往往采用统计建模和频域分析等方法,但是这些方法在处理复杂非线性信号时效果不佳。
分形分析的引入提供了一种新的思路。
通过计算信号的分形维度,并结合自相似性和分形原理,可以对信号进行特征提取和分类。
分形分析在信号处理中的应用不仅提高了信号处理的效果,还提供了更多的信息用于信号分析和识别。
总之,分形几何学和分形分析是一种对复杂结构进行研究和分析的数学工具和方法。

1引言图像分析是对图像中感兴趣的目标进行检测和测量,以获得它们的客观信息,从而建立对图像的描述,分割和特征提取把原来以像素描述的图像转变成比较简捷的非图形式的描述,是从图像到数据的过程。
这些数据是对目标特征测量的结果,或是基于测量的符号表示,描述了图像中目标的特点和性质。
图像中的目标物体一般分为人工物体和自然物体两大类。
对人为设计的三维物体进行描述的有力工具是欧几里德几何学,以及解析几何、射形几何、微分几何等。
但随着发展,人们逐渐感觉用传统几何并不能包罗万象地描述大自然中的所有对象,如海岸线、山形、河川、岩石、断裂、树木、森林、云团、闪电等等,这些不规则的对象是不能用传统的欧几里德几何学来描述的。
Benoit B.Mandelbrot 于1975年创立的分形几何学改变了这一状况,它用分形一词来表述那些没有特征长度,具有无限精细结构的图形、构造及现象。
用欧氏几何描述的对象具有一定的特征长度和标度,且成规则形状,而分形则无特征长度与标度,分形几何图形具有自相似性和递归性,易于计算机迭代,擅长描述自然界存在的景物。
2分形基础分形理论把维数视为分数,这类维数是物理学家在研究混沌吸引子等理论时需要引入的重要概念。
为了定量地描述客观事物的“非规则”程度,1919年,数学家从测度的角度引入了维数概念,将维数从整数扩大到分数,从而突破了一般拓扑集维数为整数的界限。
Mandelbrot曾经为分形下过两个定义:,称为分形集,其中,为集合部分与整体以某种形式相似的形,称为分形。
然而经过理论和应用的检验,人们发现这两个定义很难包括分形如此丰富的内容。
实际上,对于什么是分形,到目前为止还不能给出一个确切的定义,人们通常是列出分形的一系列特性来加以说明。
分形特性有:(1)分形集都具有任意小尺度下的比例细节,或者说它具有精细的结构。
分形集不能用传统的几何语言来描述,它既不是满足某些条件的点的轨迹,也不是某些简单方程的解集,是不规则的。

摘要分形是最近二三十年来才发展起来的一门新的学科,分形理论进一步可分为规则和不规则分形,不规则分形主要是描述简单的几何对象的性质和非线性系统中不光滑的和不规则的几何形式,作为一个可以用来描述很多科学现象的有效工具,它已经被广泛应用于计算机科学等许多领域,并且在各自的领域内都有了很好的理论上的发展,并且在实践性的艺术性上也有了很好的发展,大大拓宽了人们的视野,加深了人们对科学及艺术的理解。
本次毕业设计,目的是创建一个基于MATLAB的平台,简单,易于用户操作分形图软件,它应该符合经典分形图系统,具有一般分形图的功能,满足一定的图像处理、信息管理等功能。
允许用户在不理解的复杂科学理论的同时通过简单的计算机操作,改变一些参数和进行颜色调整来生成分形图形,并且进行相关图形的存储以及其他功能。
关键词:分形理论;分形艺术;分形算法;Julia集;MandelbrotAbstractFractal is developed in recent two hundred and thirty years before a new science,fractal theory can be further divided into rules and irregular fractal,irregular fractal mainly describe simple geometric objects and the properties of nonlinear system is not smooth and irregular geometrical form,as an effective tool can be used to describe a lot of scientific phenomena,it has been widely used in many fields such as computer science,and there were very good in their respective areas the development of the theory,and on the practice of artistic also have very good development,greatly widened people's horizons,deepen people's understanding of science and art.The graduation design,the purpose is to create a platform based on MATLAB,simple,easy to user operation fractal graph software,it should conform to the classic fractal graph system,has the function of general fractal figure meet certain image processing,information management,etc. Allows the user to do not understand the complex science theory at the same time,through a simple computer operation,color changing some parameters and adjust the afterlife composition form graphics,and related graphics storage,and other functions.Key words: Fractal theory; Fractal art; Fractal algorithm; Julia set; Mandelbrot目录1. 绪论 (4)1.1 研究背景 (4)1.2 研究目的和意义 (4)1.3 国内外相关课题的研究现状 (5)1.4 相关技术介绍 (6)1.4.1 MATLAB平台的选取 (6)1.4.2 关于MATLAB的GUI (6)1.5 论文组织结构 (7)2. 系统可行性分析 (8)2.1 经济可行性 (8)2.2 技术可行性 (8)2.3 社会实践可行性 (8)3. 系统需求分析 (10)3.1 系统功能结构分析 (10)3.2 分形算法原理介绍 (10)4. 系统设计 (12)4.1 系统运行界面设计 (12)4.2 软件运行环境及功能的具体设计 (12)5.系统实现 (15)5.1 分形图绘制算法的实现 (15)5.2 系统功能模块的实现 (16)5.2.1界面功能介绍 (16)5.2.2 算法功能实现 (17)5.3 系统交互模式的实现 (21)6.系统测试 (23)6.1 系统测试的目的和说明 (23)6.2 系统测试结果及不足 (27)7.总结 (28)参考文献: (29)致谢.............................................................................................. 错误!未定义书签。

fractals指标Fractals指标是基于“分形几何”理论的技术分析指标。
所谓分形,是指在任何比例上的自相似性,即某个结构中的一部分在其它层次的结构中也有出现,而且出现的方式和规律相同。
Fractals指标利用这种分形特征,通过寻找市场重要的高低点,来提供交易指示。
举个例子,我们可以看一看日图中的全球最大资本管理公司:贝莱德,分形指示的效果。
从图中可以看出分形指标的效果非常不错,几乎在每个市场波动中,都有明显的高低点形成。
(图1:贝莱德点差日线图)图中显示的圆圈就表示了分形点,当市场走势突破分形点时,就会有较大的概率进一步走向相反的方向。
因此,分形指标可以被看作是一种密实的支撑和阻力水平的交叉确认技术,可以帮助交易者确认市场的趋势和方向,从而更好地制定交易策略并做出决策。
Fractals指标通过寻找市场中的“波峰”和“波谷”来确定价格的发展方向。
在图表中,每个波峰和波谷都被认为是一个分形点。
分形点有两种形式:上行的分形点(表示市场中的“波峰”)和下行的分形点(表示市场中的“波谷”)。
在一个典型的分形指标中,至少需要四个连续的价格点才能形成一个波峰或波谷。
在分形指标中,波峰通常表示最高价,并伴随着分形点的出现。
波谷则表示最低价,通常也会有分形点的存在。
通过寻找这些分形点,分形指标可以提供有关价格的重要信息:市场的高低点和未来价格的方向。
在计算分形指标时,我们需要寻找这里所说的“运行最高价”和“运行最低价”。
在确定“运行最高价”时,我们需要首先找到当前价格周期中的最高价。
然后,我们需要观察此价格点左侧的两个价格点。
如果当前最高价比这两个价格点都高,那么我们就找到了一个波峰点,表示当前市场的高点。
反之,如果当前最高价并不比这两个价格点都高,那么我们将跳过这个点,继续寻找下一个点。
相应地,当我们确定“运行最低价”时,我们需要找到当前价格周期中的最低价。
然后,我们需要观察此价格点左侧的两个价格点。
如果当前最低价比这两个价格点都低,那么我们就找到了一个波谷点,表示当前市场的低点。
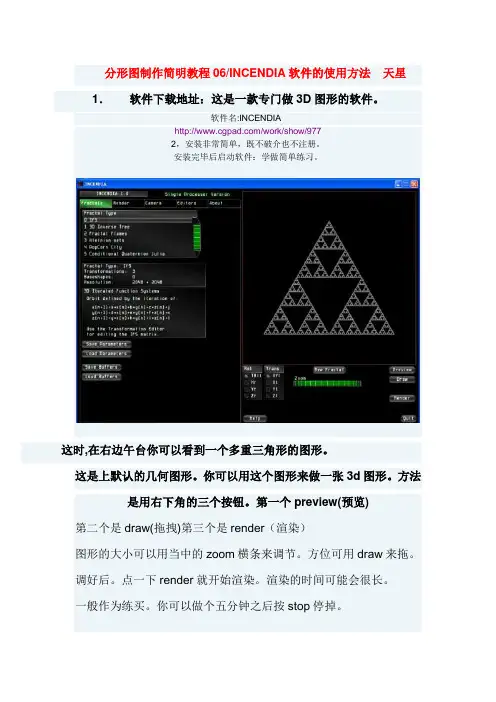
分形图制作简明教程06/INCENDIA软件的使用方法天星1.软件下载地址:这是一款专门做3D图形的软件。
软件名:INCENDIA/work/show/9772,安装非常简单,既不破介也不注册。
安装完毕后启动软件:学做简单练习。
这时,在右边午台你可以看到一个多重三角形的图形。
这是上默认的几何图形。
你可以用这个图形来做一张3d图形。
方法是用右下角的三个按钮。
第一个preview(预览)第二个是draw(拖拽)第三个是render(渲染)图形的大小可以用当中的zoom横条来调节。
方位可用draw来拖。
调好后。
点一下render就开始渲染。
渲染的时间可能会很长。
一般作为练买。
你可以做个五分钟之后按stop停掉。
3.对刚才渲染的3D图形作彩色处理。
打开render的界面。
在中间有二个园形图案。
点击它可以定义图形和背景的彩色。
在彩色表中选中彩色。
点一下ok.彩色就会调整。
4.最后点左上角的saveBitmap即可以存出图片(bmp格式)存出来的图片格式是bmp。
而且尺寸较大。
你可以缩小转换为jpg格式。
体积会小很多。
好了最简单的3d作品做好了。
是不是很简单。
分形图制作简明教程07/INCENDIA软件的使用方法之二天星把incendia软件比喻为一个具有亿万图片的图库并不过份。
而且也并非确切。
其一用它做出的图片是无限数的。
其二用它做出的图片是没有重复的。
即便你选用相同的参数图形也不一致。
因为其中含有随机参数。
当然要取出这些无穷无尽的图片,确实需要一定的练习。
下面我们共同的演练一下。
1.打开软件。
午台上总是出现那张生硬的三角形图形。
不用着急。
这跟电脑的《开始》键相似。
一切从这里出发!2.再打开编辑器<editors>,在左上角勾选一下edit,午台显出虚线的图片。
再点一下菜单new.在左面板上就出现了48种效果图.我们先选用一个最简单的《园球效果》来试试(用鼠标点击它)这时《效果》就跳进右边的午台上。

学习分形形了解分形形的特点和构造方法学习分形:了解分形的特点和构造方法分形(fractal)一词由波兰数学家曼德尔布罗特(Benoit Mandelbrot)于1975年引入,用于描述一类自相似的几何图形或物体。
分形具有许多独特的特点,如无穷细节、复杂性、自相似性等。
本文将介绍分形的特点和构造方法。
一、分形的特点1. 无穷细节:分形具有无穷多的细节和复杂性,无论放大或缩小图像,都能够发现新的细节。
这使得分形在数学、自然科学和艺术等领域具有广泛应用。
2. 自相似性:分形是自相似的,即整体的结构与其局部结构相似。
无论是整体还是局部的形状都能够在较小或较大的尺度上找到相似的结构。
这种自相似性是分形的重要特征。
3. 复杂性:分形的复杂性指的是其结构和形态的复杂程度。
相比于传统的几何图形,分形形状更为复杂,无法用简单的几何形状或方程式描述。
4. 维度非整:分形的维度通常是非整数维的,例如,柯赛雪垫(Koch曲线)的维度介于1和2之间。
这种非整数维度是分形与传统几何学的重要区别之一。
5. 噪声与规则性:分形能够通过噪声与规则性的结合来表现出不规则的形态。
分形结构的噪声性质使得其在模拟自然界中的山脉、云朵等不规则物体时非常逼真。
二、分形的构造方法1. 迭代函数系统(IFS):迭代函数系统是构造分形图形的一种常用方法。
它通过对函数的重复应用来生成自相似结构。
柯赛雪垫和谢尔宾斯基地毯(Sierpinski carpet)都是通过迭代函数系统构造的。
2. 分形树:分形树是用于模拟植物的分枝结构的一种方法。
通过对树干进行重复分支并在每个分支的末端再次生成分支,可以构造出栩栩如生的分形树形结构。
3. 噪声函数:噪声函数是基于随机数生成的分形图形构造方法之一。
通过使用不同频率和振幅的噪声函数叠加,可以产生具有细节丰富的分形图像。
4. 分形几何的数学公式:柯赛雪垫、曼德尔布罗特集合等分形图形可以使用数学公式进行描述和生成。



基于分形几何的分形图绘制与分析摘要:基于分形几何的分形图绘制方法源于L系统、迭代函数系统IFS、复动力系统等。
在运用分形原理及算法编程绘制多种分形图的基础上,重点对IFS参数进行实验分析,IFS吸引集实现了对原图形的几何变换。
分形图的演变具有渐变性。
关键词:分形几何迭代函数系统分形图绘制渐变1 分形几何学现代数学的一个新的分支——它是由美籍法国数学家曼德勃罗(B.B.Mandelbrot)1973年在法兰西学院讲课时,首次提出了分形几何的设想。
分形(Fractal)一词,是曼德勃罗创造出来的,其原意具有不规则、支离破碎等意义,分形几何学是一门以非规则几何形态为研究对象的几何学。
由于不规则现象在自然界是普遍存在的,因此分形几何又称为描述大自然的几何学。
分形几何的诞生无论是在理论上还是在实践上都具有重要价值。
2 分形的定义目前分形还没有最终的科学定义,曼德勃罗曾经为分形下过两个定义。
4.2 基于IFS迭代函数系统的分形图绘制迭代函数系统(Iteration Function System,简称IFS)是分形几何学的重要分支,它也是分形图像中最富生命力并具有广阔应用前景的领域之一。
IFS是M.F.Barnsley于1985年发展的一个分形构形系统。
IFS 的理论包括以下几方面的内容:压缩映射、度量空间、不变紧缩集的存在以及测度理论等。
迭代函数系统在一大类物体的建模问题中具有很大的优势,特别是对自然景物的计算机模拟生成优势更为明显。
实际上,只需给出几个仿射变换的系数,就可基本确定一个物体的迭代函数系统。
正因为如此,IFS在图形学中有着广泛的应用。
其中,可视化技术的研究由2D分形对象拓广到3DFractal;由IFS研究的自相似的分形图扩大了其应用范围,IFS变换不必仅限于仿射变换;在用IFS建摸的研究中,实现了对原图形的几何变换,将IFS中的线形变换推广到非线形变换;对自然景物计算机生成问题的探讨,其建摸方法亦由二维推广到三维。

分形几何有许多典型的范例,以下是其中一些:
1. 谢尔宾斯基三角形:这是一种自相似的分形图形,通过不断将三角形划分为更小的三角形,最终得到具有无限复杂性的图形。
2. 谢尔宾斯基垫片:这是由谢尔宾斯基三角形进一步演化而来的一种分形图形,由三角形内部的三角形构成,整体呈现出一个自相似的模式。
3. 科赫曲线:又称为科赫雪花或科赫蛇,是一种分形曲线。
通过不断将一段线段分割成等长的两段,然后将每一段线段的中间部分弯曲成等边三角形,最终得到具有无限复杂性的图形。
4. 曼德布罗集:这是由数学家本华·曼德布罗提出的分形图形,通过不断将单位正方形进行切割和填充,最终得到的图形是一个具有无限复杂性的集合。
5. 皮亚诺曲线:这是一种由意大利数学家皮亚诺提出的分形图形,它是一种在平面上的连续曲线,通过不断将线段进行延长和弯曲,最终得到的图形具有无限复杂性和自相似性。
这些只是分形几何中的一些典型范例,实际上还有许多其他的分形图形和结构,如朱利亚集、费根堡姆曲线等。
这些分形图形的特点是具有无限的复杂性和自相似性,并且在许多领域中得到了应用。

分形初步认识分形和制作简单的分形形分形:初步认识分形和制作简单的分形形分形(fractal)是指一种具有自相似性质的几何图形或数学模型。
在这些图形或模型中,无论放大多少次,都能够看到与整体形状相似的部分。
分形的研究起源于上世纪60年代,由波尔兹曼首次提出,并由Mandelbrot在上世纪70年代进一步发展和推广。
分形在数学、物理、生物、艺术等领域都有广泛的应用。
一、分形的基本概念和特征分形的核心特征包括自相似性、无穷细节和分形维度。
自相似性指的是一个物体的一部分与整体之间存在相似的结构,而无穷细节则是指分形的结构可以不断被放大,仍然能够展示出更多的细节。
分形维度是描述分形形状复杂程度的重要参数,它可以是非整数维度。
二、常见的分形图形和模型1. 科赫曲线(Kochcurve):科赫曲线是一种无限细分的闭合曲线,它由无数个相似的小线段组成,每个小线段都与整体曲线形状相似。
制作科赫曲线的方法很简单,首先取一条线段,然后将线段等分为三段,再在中间段上构建一个等边三角形,最后去掉中间那段线段,将剩余的线段作为新的整体,重复以上操作。
2. 曼德勃罗集合(Mandelbrot Set):曼德勃罗集合是由复变函数产生的一类分形,它可以在复平面上绘制出具有自相似性的图形。
曼德勃罗集合的生成过程非常复杂,一般需要通过计算机程序来绘制。
三、制作简单的分形形状1. 制作分形树:分形树是一种常见的分形图形,它模拟了自然界中的树木形状。
制作分形树的方法很简单,首先绘制一条竖直线段作为树干,然后在树干的两侧分别绘制两条较短的线段,形成树干的两个分支。
再对每个分支递归地应用相同的绘制规则,直到达到预设的层数。
2. 制作谢尔宾斯基三角形(Sierpinski Triangle):谢尔宾斯基三角形是一种经典的分形形状,它由无数个自相似的小三角形组成。
制作谢尔宾斯基三角形的方法很简单,首先绘制一个大三角形,然后将它分割为四个相似的小三角形,接着去掉中间那个小三角形,再对每个剩余的小三角形递归地应用相同的操作,直到达到预设的层数。
CAD模型的分形处理方法
CAD模型的分形处理方法是指通过分形几何理论,将CAD模型进行细节处理,从而实现模型更加真实和自然的效果。
下面我们来介绍一些常见的CAD模型分形处理方法。
一、分形结构生成法
分形结构生成法是构建分形CAD模型的基本方法之一,它通
过分形算法生成一些基本的几何形状,然后通过复制、旋转和缩放等操作,不断生成更加细致和复杂的结构。
例如,我们可以选用分形算法中的分形树算法和分形蕨算法来构建植物的CAD模型。
首先,我们选择一个基本的草木纹样,然后通过递归地生成更加细致的草木纹样,最终构建出真实的植物CAD模型。
二、分形纹理生成法
分形纹理生成法是利用分形算法生成纹理来建立CAD模型的
方法之一,它可以实现一些复杂纹理效果,如云彩、火焰、水波、石头表面等等。
例如,在CAD模型中,我们可以用分形算法生成一个石头表
面的纹理,然后将该纹理映射到CAD模型表面上。
这样,我
们就能得到一个真实的石头模型,同时还能保留石头的细节和自然特性。
三、分形噪声生成法
分形噪声生成法是一种为CAD模型添加噪声的方法,它通过
分形算法创建纹理噪声,从而为CAD模型增加了更多的细节。
例如,在建立一个人物CAD模型时,我们可以使用分形噪声
算法来生成肌肉、皮肤和头发的纹理。
这样,我们就能得到一个更加真实和自然的人物模型。
总之,分形处理在CAD模型中的应用范围十分广泛,通过合
理使用分形算法,我们可以构建出更加真实、自然和细致的CAD模型。
-060-2020年第17期(总第217期)摘 要:在分形几何融入中学数学的教学中,几何画板利用其强大的迭代功能创设新的教学情境,为中学数学课堂中分形几何的教学提供了便利。
文章以几何画板生成勾股树为例,简要分析分形几何在中学数学中的美学价值以及教育价值,目的在于促进分形几何与中学数学的融合,让学生在学习分形几何的过程中,感受数学之美,提高学习兴趣,发展数学核心素养。
关键词:勾股树;分形几何;美学价值;教育价值中图分类号:G633.6文章编号:2095-624X(2020)17-0060-03一、迭代与分形概述1.迭代迭代是几何画板中一个基本且重要的功能,主要有两种形式:一般迭代和深度迭代。
一般迭代类似于函数的映射,是指按一定的迭代规则,从原像到像的反复映射过程,是一种重复反馈过程的活动,需要通过改变迭代的次数来改变迭代深度;深度迭代是在一般迭代基础上的一种带参数的迭代,可以直接通过改变参数的值而改变迭代深度。
2.分形几何分形最初是指不规则的、分数的且具有自相似性的图形或现象,后来,数学家曼德布罗特在定义分形图形时,给出了分形的定义:分形即意味着其维数不是整数而是分数,并且这些分量在某种程度上与整体相似;分形几何就是研究无限复杂但具有一定意义的自相似图形和结构的几何学。
二、勾股树及其生成在中学几何中,勾股定理具有不可替代的地位,描绘了直角三角形三条边之间特定的关系。
古希腊数学家毕达哥拉斯在勾股定理的基础上,按照满足勾股定理的直角三角形的三边画出来一个可以无限次重复的图形,因屡次反复之后所生成的图形的外观像一棵树,因此称作勾股树,如图1。
由于勾股树生成结构与图形的重复性,因此可以利用几何画板的迭代功能来制作。
本文中勾股树的制作是在中文版几何画板5.0的基础上完成的[1]。
观察图1,勾股树可以看作是在其“树干”的基础上进行多次迭代而形成的,具体来看:先作一条线段,并以这条线段为边作正方形,以其对边作为直角三角形的斜边,并在斜边基础上作出其他两条直角边,然后以这两条直角边为新的边,作出两个小的正方形,得到如图2所示的图形,称为勾股图,又称为一代勾股树;然后在此基础上,不断地重复这一过程,当重复次数足够多时,得基于几何画板浅谈分形几何的价值翟玉秀(扬州大学数学科学学院,江苏 扬州 225000)文献标识码:A——以勾股树为例到一个树状的结构,即为勾股树。
Wobble分形算法简介Wobble分形算法是一种基于几何变换的分形生成方法,它通过迭代不同尺度的抖动变换来生成具有自相似性的分形图形。
Wobble分形算法源自于数学家Michael Barnsley在1988年提出的分形理论。
通过对图形进行随机的微小扰动,Wobble分形能够生成富有变化和细节的分形图案,具有极高的艺术美感和视觉冲击力。
基本原理Wobble分形算法的基本原理是通过对一幅原始图形进行多次几何变换,每次变换时都对图形进行随机的抖动。
具体步骤如下:1.绘制初始图形:首先绘制一个基本形状的图形,可以是简单的几何图形如矩形、三角形,也可以是复杂的曲线图形。
2.随机抖动:对初始图形进行随机的微小扰动,使每个点的坐标发生细微的变化。
这种扰动可以是平移、旋转、缩放等任意变换,也可以结合多种变换方式。
3.迭代变换:对抖动后的图形再次进行几何变换,重复步骤2,得到一组新的图形。
4.终止条件:迭代变换的次数根据需要设定,在达到指定次数后停止变换,得到最终的分形图案。
算法流程下面是Wobble分形算法的基本流程:1.初始化:选择初始图形和设定迭代次数。
2.迭代变换:1.对初始图形进行随机抖动,得到一组新的图形。
2.对新的图形进行进一步的变换,重复步骤2.1。
3.记录每次变换后的图形,存储为一组分形图案。
4.如果迭代次数达到指定次数,转到步骤3;否则转到步骤2.1。
3.输出分形图案。
算法优化Wobble分形算法可以进行多种优化,以提高生成的分形图案质量和效率。
以下是一些常见的优化技巧:1.随机性控制:通过控制抖动时的随机性,可以调整生成的分形图案的复杂度和形态。
可以使用特定的随机数生成方法,如分布均匀的伪随机数生成器。
2.变换参数控制:调整几何变换的参数,如平移、旋转、缩放的幅度和比例,可以改变生成的分形图案的形态。
通过细致调整变换参数,可以得到更加丰富多样的分形图案。
3.增量绘制:在生成分形图案时,可以采用增量绘制的方式,即每次变换只绘制部分图形,避免重复绘制已经生成的图形。
一、实验目的1. 理解分形的基本概念及其在自然界和科学中的应用。
2. 掌握分形图形的生成方法,包括迭代和递归。
3. 通过计算机实现Koch曲线、Sierpinski三角形和Cantor集等经典分形图形。
4. 分析分形图形的几何特性,如自相似性、无限细节和分形维数。
二、实验原理分形是一种具有无限复杂性和自相似性的几何形状。
它可以通过迭代和递归的方法生成,具有以下特点:1. 自相似性:分形图形的任何部分都与整体具有相似的结构。
2. 无限细节:分形图形在放大后仍然具有复杂的结构。
3. 分形维数:分形维数介于传统几何维数(如一维、二维、三维)之间,可以用来描述分形图形的复杂程度。
三、实验内容1. Koch曲线实验目的:生成Koch曲线,观察其自相似性和无限细节。
实验步骤:- 选择一条初始线段。
- 将线段等分为三部分,删除中间部分,并在两侧各添加一个等长的线段,形成60度角。
- 对新形成的四个线段重复上述步骤。
实验结果:通过迭代,Koch曲线逐渐呈现出复杂的结构,表现出自相似性和无限细节。
2. Sierpinski三角形实验目的:生成Sierpinski三角形,观察其自相似性和无限细节。
实验步骤:- 选择一个等边三角形作为初始图形。
- 在每个等边三角形的每个顶点处,向下作等边三角形的高,将其等分为三个小三角形。
- 保留中间的小三角形,删除其余部分。
实验结果:通过迭代,Sierpinski三角形逐渐呈现出复杂的结构,表现出自相似性和无限细节。
3. Cantor集实验目的:生成Cantor集,观察其分形维数和无限细节。
实验步骤:- 选择一个线段作为初始图形。
- 将线段等分为三部分,删除中间部分。
- 对新形成的两个线段重复上述步骤。
实验结果:通过迭代,Cantor集逐渐呈现出复杂的结构,具有无限细节。
其分形维数为ln(2)/ln(3) ≈ 0.6309,介于一维和二维之间。
四、实验结果与分析1. 通过实验,我们成功生成了Koch曲线、Sierpinski三角形和Cantor集等经典分形图形,验证了分形的基本概念和特性。
分形图形生成原理探究随着计算机技术的不断发展,分形图形在数字艺术、自然科学和工程领域中得到广泛应用。
分形是一种具有自相似性质的数学对象,其生成原理深受人们的关注。
本文将探究分形图形的生成原理,介绍分形的基本概念,以及常用的分形生成算法。
一、分形的基本概念分形是一种具有自相似性质的几何图形。
即整体结构和局部细节之间存在某种相似关系,不论放大还是缩小,都可以看到相同的图形。
分形的自相似性质使得它们具有无限的细节和复杂度。
二、分形图形的生成原理1. 迭代运算迭代运算是生成分形图形的常用方法之一。
这种方法通过重复应用某种变换或映射规则,不断生成新的图形。
具体步骤如下:- 首先选定一个初始图形,例如一个简单的线段或几何形状。
- 然后根据一定的规则进行变换或映射操作,生成下一级的图形。
- 重复上述步骤,直到达到期望的分形效果。
迭代运算可以产生各种各样的分形图形,如科赫曲线、谢尔宾斯基三角形等。
2. 噪声函数噪声函数是通过随机性来生成分形图形的一种方法。
噪声函数可以产生随机性纹理或图案,并通过适当的参数调节,实现分形效果。
生成分形图形的基本步骤如下:- 首先定义一个噪声函数,它可以是简单的随机数生成器或更复杂的数学函数。
- 然后使用噪声函数来计算每个像素的数值或颜色,从而生成图像。
噪声函数可以用于生成山脉、云彩等具有分形特征的自然图像。
三、常用的分形生成算法1. 递归细分递归细分是一种通过使用分形规则进行逐级细分的方法。
它基于拆分和替代的原则,不断将图形细分为更小的部分,然后用更小的部分替代原有的部分。
递归细分可以生成多种复杂的分形图形,如分形树、雪花等。
2. 碎形图像编码碎形图像编码是一种基于碎形压缩理论的分形生成方法。
它通过找到一组变换规则和关联函数,将整个图像分割成小的区域,然后用适当的变换规则对每个区域进行编码。
这种方法可以生成高质量的分形图像,并用较小的存储空间保存。
3. 分形几何建模分形几何建模是一种通过将分形规则应用于三维空间中的几何体来生成分形图形的方法。
基于分形几何的分形图绘制与分析
摘要:基于分形几何的分形图绘制方法源于l系统、迭代函数系统ifs、复动力系统等。
在运用分形原理及算法编程绘制多种分形图的基础上,重点对ifs参数进行实验分析,ifs吸引集实现了对原图形的几何变换。
分形图的演变具有渐变性。
关键词:分形几何迭代函数系统分形图绘制渐变
1 分形几何学
现代数学的一个新的分支——,它是由美籍法国数学家曼德勃罗(b.b.mandelbrot)1973年在法兰西学院讲课时,首次提出了分形几何的设想。
分形(fractal)一词,是曼德勃罗创造出来的,其原意具有不规则、支离破碎等意义,分形几何学是一门以非规则几何形态为研究对象的几何学。
由于不规则现象在自然界是普遍存在的,因此分形几何又称为描述大自然的几何学。
分形几何的诞生无论是在理论上还是在实践上都具有重要价值。
2 分形的定义
目前分形还没有最终的科学定义,曼德勃罗曾经为分形下过两个定义:
(1)分形是hausdorff-besicovitch维数严格大于拓扑维数的集合。
因为它把许多hausdorff维数是整数的分形集合排除在外,例如,经典分形集合peano曲线分形维数
(2)局部与整体以某种方式自相似的形,称为分形。
然而,经过理论和应用的检验,人们发现这两个定义很难包括分形
如此丰富的内容。
实际上,对于什么是分形,到目前为止还不能给出一个确切的定义,正如生物学中对“生命”也没有严格明确的定义一样,人们通常是列出生命体的一系列特征来加以说明。
对分形的定义也可同样的处理。
(ⅰ) 分形集合在任意小尺度下,它总有复杂的细节,或者说它具有精细的结构。
(ⅱ) 分形集合是非常不规则的,用传统的几何语言无法来描述它的局部和整体,它既不是满足某些条件的点的轨迹,也不是某些简单方程的解集。
(ⅲ) 分形集具有某种自相似形式,可能是近似的自相似或者统计的自相似。
(ⅳ) 以某种方式定义的分形集合的“分形维数”,严格大于它相应的拓扑维数。
(ⅴ) 在大多数令人感兴趣的情形下,分形集合是以非常简单的递归的方法产生的。
3 分形研究的对象
几何学的研究对象是物体的形状,在自然界中,许多物体的形状是极不规则的,例如:弯弯曲曲的海岸线,起伏不平的山脉,变化无偿的浮云,以及令人眼花缭乱的满天繁星,等等。
这些物体的形状有着共同的特点,就是极不规则,极不光滑。
但是,所有的经典几何学都是以规则而光滑的形状为其研究对象的,例如:初等平面几何的主要研究对象是直线与圆;平面解析几何的主要研究对象是一
次曲线与二次曲线;微分几何的研究对象是光滑的曲线与曲面;代数几何的研究对象则是复空间中的代数曲线,等等。
把凹凸不平的地球表面看成是绝对光滑的球面或椭球面。
虽然在许多情况下,这样做并不妨碍我们得到非常符合实际的结论,但是,随着人类对客观世界的认识的逐步深入以及科学技术的不断进步,这种把不规则的物体形状加以规则化,然后进行处理的做法已经不另人满意了。
在70年代中期,一门新型的几何学脱颖而出——分形几何学,就是用来深刻地描述大自然本身的几何学,它能深刻地刻划大千世界充满奇异而神秘的各种极不规则极不光滑的对象,这是数学发展史上的一个新世界。
事实上,可以把分形看作是自然形态的几何抽象。
4 分形图绘制与分析
4.1 基于l系统的分形图绘制
l系统是生物学家lindenmayer于1968年从植物形态学角度提出的一套用以描述植物树木的方法,开始时只着重于植物的拓扑结构,即植物组件之间的相邻关系,后来才把几何解释加进描述过程,形成后来的l系统。
这个系统的高度简洁性和多级结构,为描述植物树木生长和繁殖过程的形态和结构特征,提供了行之有效的理论和方法。
l系统不但能描述植物,而且其构图方法也可用来绘制各类有规则分形曲线及其它形状。
l系统是基于符号重写系统。
即用一个重写规则逐次地置换初始对象的各个部分来确定一个复杂的对象。
分形l系统可以模拟各种植
物的形状。
根据不同的改写规则,可以画出不同的植物形,用于模拟自然景观可达到形象、逼真的效果。
如图1所示。
4.2 基于ifs迭代函数系统的分形图绘制
迭代函数系统(iteration function system,简称ifs)是分形几何学的重要分支,它也是分形图像中最富生命力并具有广阔应用前景的领域之一。
ifs是m.f.barnsley于1985年发展的一个分形构形系统。
ifs的理论包括以下几方面的内容:压缩映射、度量空间、不变紧缩集的存在以及测度理论等。
迭代函数系统在一大类物体的建模问题中具有很大的优势,特别是对自然景物的计算机模拟生成优势更为明显。
实际上,只需给出几个仿射变换的系数,就可基本确定一个物体的迭代函数系统。
正因为如此,ifs在图形学中有着广泛的应用。
其中,可视化技术的研究由2d分形对象拓广到3dfractal];由ifs研究的自相似的分形图扩大了其应用范围,ifs 变换不必仅限于仿射变换];在用ifs建摸的研究中,实现了对原图形的几何变换],将ifs中的线形变换推广到非线形变换];对自然景物计算机生成问题的探讨,其建摸方法亦由二维推广到三维。
如图2基于ifs迭代函数系统所绘制的三维树叶分形图。
另外,由于ifs代码可以描述形态各异的对象,这就意味着可以用极少量的数据,就可描述复杂的图像图形,因而ifs具有很强的图形数据压缩能力。
4.3 基于ifs迭代参数渐变的分形图绘制与分析
用ifs(interated function systerm)产生分形图:
以表1中的参数为迭代码可以产生sirpinski三角形,见图3(a)所示。
(a)按表1参数绘制的sirpinki 三角形 (b) d4=0.3 时情况 (c) 按表1参数绘制的树叶
只改动参数d4=0.3,则可以生成图3(b)示sirpinski三角形。
以表2中的参数为迭代码可以产生一个树叶,如图3(c)所示。
把树叶迭代码与sirpinski三角形迭代码之间缩小差距,缩小比例为0.25、0.75,可以看到逐渐向三角形过渡,如图4所示。
4.4 基于复动力系统的分形图绘制
复动力系统的分形集合主要包括mandelbrot集和julia集。
mandelbrot集是分形中最著名的分形集合,它是分形创始人mandelbrot在非线性领域中作出的杰出贡献。
julia集是在本世纪初法国数学家g.julia和p.fatou分别研究过的一种多项式和有理函数的迭代,当时由于缺乏相应的图形工具而使研究中断,直到计算机图形学的出现才使其重获生机。
mandelbrot集和julia集都是通过在复平面中g(z)=z2+c的反复迭代而得到的点的序列,其中c 和z均为复数。
由julia集与mandelbrot集呈现在人们面前的美妙图象令艺术家们叹为观止,将这种艺术图形用于纺织印染、广告印刷、工业设计、邮票制作、服装设计及计算机教学等方面,其经济效益和社会效益均具有广阔的应用前景。
5结语
分形几何学是一门以非规则几何形态为研究对象的几何学。
分形图
形绘制的方法有l系统、迭代函数系统ifs、复动力系统等。
ifs 吸引集实现了对原图形的几何变换。
分形图的演变具有渐变性。
参考文献
[2] 刘甲.ifs交互式参数控制算法研究与应用[j].信息技术与信息化.2011
[3] 李常.一种基于广义m —j集的安全底纹设计方法[j].计算机应用与软件.201。