角平分线等腰三角形
- 格式:doc
- 大小:65.50 KB
- 文档页数:2

三角形中的特殊模型-平分平行(射影)构等腰、角平分线第二定理模型角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,,本专题就角平分线的非全等类模型作相应的总结,需学生反复掌握。
平分平行(射影)构等腰模型、角平行线第二定理模型(内角平分线定理和外角平分线定理模型)平分平行(射影)构等腰1)角平分线加平行线必出等腰三角形.模型分析:由平行线得到内错角相等,由角平分线得到相等的角,等量代换进行解题.平行线、角平分线及等腰,任意由其中两个条件都可以得出第三个。
(简称:“知二求一”,在以后还会遇到很多类似总结)。
平行四边形中的翻折问题就常出现该类模型。
图1图2图3条件:如图1,OO'平分∠MON,过OO'的一点P作PQ⎳ON. 结论:△OPQ是等腰三角形。
条件:如图2,△ABC中,BD是∠ABC的角平分线,DE∥BC。
结论:△BDE是等腰三角形。
条件:如图3,在△ABC中,BO平分∠ABC,CO平分∠ACB,过点O作BC的平行线与AB,AC分别相交于点M,N.结论:△BOM、△CON都是等腰三角形。
2)角平分线加射影模型必出等腰三角形.→图4条件:如图4,BE平分∠CBA,∠ACB=∠CDA=90°. 结论:三角形CEF是等腰三角形。
1(2023·浙江·八年级假期作业)如图,已知∠AOB,以点O为圆心,以任意长为半径画弧,与OA、OB分别于点C、D,再分别以点C、D为圆心,以大于12CD为半径画弧,两弧相交于点E,过OE上一点M作MN∥OA,与OB相交于点N,∠MOB=50°,则∠AOM=.【答案】25度/25°【分析】通过两直线平行,同位角相等,再利用角平分线定义求解即可.【详解】∵MN∥OA,∴∠AOB=∠MNB=50°,由题意可知:OM平分∠AOB,∠AOB=25°.故答案为:25°.∴∠AOM=∠MOB=12【点睛】本题考查了基本作图,作已知角的角平分线及其定义和平行线的性质,解此题的关键是熟练掌握基本作图和平行线的性质及角平分线定义的应用.2(2023·浙江·八年级期中)如图,已知△ABC的两边AB=5,AC=8,BO、CO分别平分∠ABC、∠ACB,过点O作DE∥BC,则△ADE的周长等于.【答案】13【分析】根据BO平分∠CBA,CO平分∠ACB,且ED∥BC,可得出OD=OB,OE=OC,所以三角形ADE的周长是AB+AC.【详解】解:∵BO平分∠CBA,CO平分∠ACB,∴∠DBO=∠OBC,∠OCE=∠OCB,由∵DE∥BC,∴∠DOB=∠OBC,∠EOC=∠OCB,∴∠DBO=∠DOB,∠EOC=∠ECO,∴DO=DB,EO=EC,·又∵AB=5,AC=8,∴ADE的周长=AD+DE+AE=AB+AC=13【点睛】本题主要考查了角平分线的定义、平行线的性质以及等腰三角形的判定,其中运用角平分线的定义和平行线的性质创造等腰三角形的条件是关键.3(2023·广东·八年级期末)如图,▱ABCD中,AB=3cm,BC=5cm,BE平分∠ABC交AD于E点,CF 平分∠BCD交AD于F点,则EF的长为cm.【答案】1【分析】根据角平分线的概念、平行线的性质及等腰三角形的性质,可分别推出AE=AB,DF=DC,进而推出EF=AE+DF-AD.【详解】∵四边形ABCD是平行四边形,∴∠AEB=∠EBC,AD=BC=5cm,∵BE平分∠ABC,∴∠ABE=∠EBC,则∠ABE=∠AEB,∴AB=AE=3cm,同理可证:DF=DC=AB=3cm,则EF=AE+FD-AD=3+3-5=1cm.故答案为:1.【点睛】本题考查了平行四边形的性质,关键是运用角平分线的概念和平行线的性质,由等角推出等边.4(2023.江苏八年级期中)如图,已知:在△ABC中,∠BAC=90°,AD⊥BC于D,∠BCA的角平分线交AD与F,交AB于E,FG⎳BC交AB于G.AE=4cm,AB=12cm,则BG=,GE=.【答案】4cm;4cm.【详解】过E作EH垂直BC交BC于H点,易证△AEC≌△EHC;由角度分析易知∠AEF=∠AFE,即AE=AF,则有EH=EA=AF;又可证△AGF≌△BHE,则AG=EB=12-4=8,则BG=8-4=4,GE=4.【点睛】这道题主要讲解角平分线加射影模型必出等腰三角形的模型.角平行线第二定理(内角平分线定理和外角平分线定理)模型1)内角平分线定理图1图2图3条件:如图1,在△ABC中,若AD是∠BAC的平分线。
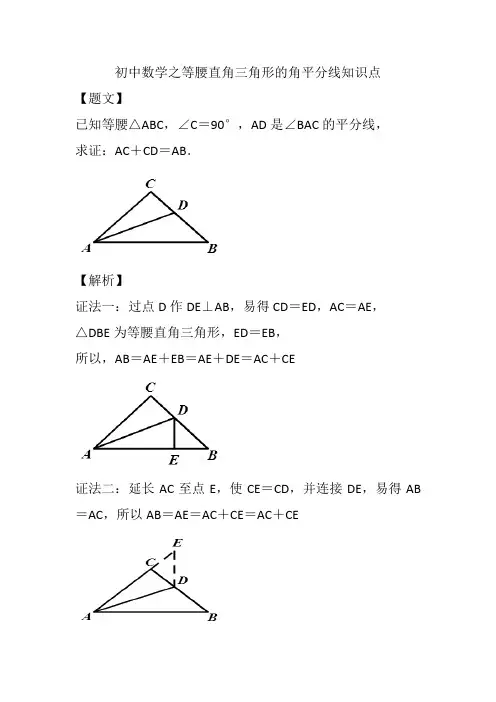
初中数学之等腰直角三角形的角平分线知识点
【题文】
已知等腰△ABC,∠C=90°,AD是∠BAC的平分线,
求证:AC+CD=AB.
【解析】
证法一:过点D作DE⊥AB,易得CD=ED,AC=AE,
△DBE为等腰直角三角形,ED=EB,
所以,AB=AE+EB=AE+DE=AC+CE
证法二:延长AC至点E,使CE=CD,并连接DE,易得AB =AC,所以AB=AE=AC+CE=AC+CE
证法三:延长BC至点E,使CE=BC,连接AE,
则AE=AB(垂直平分线的性质),
易得∠EAD=∠EDA=22.5°+45°=67.5°,
则AB=AE=ED,
所以AB=ED=EC+CD=BC+CD=AC+CD
证法四:过点C作CG⊥AB,垂足为点F,交AD于点E,使得CF=GF,并连接AG,
易得AF=GF=BF=CF,AB=CG,AG=BC=AC,
又得∠CED=∠CDE=∠AEG=∠EAG=67.5°,
所以CE=CD,AG=EG,
所以AB=CG=EG+CE=AC+CD
证法五:延长AC至点E使得CE=CD,并连接BE,易得△ACD≌△BCE,∠E=∠ADC=∠ABE=67.5°,则AE=AB,
所以AB=AC+CE=AC+CD
证法六:易得S△ACD:S△ADB=CD:DB=AC:AB,设AC=CB=1,则AB=,CD=x,BD=1-x
代入比例式x:(1-x)=1:,
∴x=-1,
所以AC+CD=1+-1==AB。


等腰三角形的性质与定理等腰三角形是指具有两条边长度相等的三角形。
在几何学中,等腰三角形具有一些独特的性质和定理。
本文将对等腰三角形的性质与定理进行详细的介绍。
一、等腰三角形的定义和性质等腰三角形的定义:等腰三角形是指具有两条边的长度相等的三角形。
在等腰三角形ABC中,若AB=AC,则∠B=∠C。
等腰三角形的性质:1. 等腰三角形的底角(底边上的角)两个相等。
证明:由等腰三角形的定义可知,AB=AC,再加上三角形内角和为180度的性质,可得∠A+∠B+∠C=180度。
由于∠A=∠B=∠C,所以∠B+∠B+∠B=180度,即3∠B=180度,所以∠B=∠C=60度。
2. 等腰三角形的高(从顶点到底边的垂直线段)和斜边的中线相等。
证明:作等腰三角形ABC的高AD和BC的中线DE。
首先证明AD=DE。
由于三角形ABC是等腰三角形,所以∠A=∠B=∠C=60度。
又因为∠DAB和∠DEC是等腰三角形的底角,所以∠DAB=∠DEC=60度。
因此,由三角形内角和为180度的性质可知,∠DAB+∠BAD+∠BDA=180度,即60度+∠BAD+90度=180度,解得∠BAD=30度。
同理,∠DCE=30度。
再考虑三角形ABD和DEC,由于∠BAD=∠DCE=30度,∠DAB=∠DEC=60度,所以根据AA相似性质可知,∠ABD=∠DEC,故两个三角形相似。
根据相似三角形的性质,可得AD/DE=BD/EC=AB/DC=1/2。
又已知BD=DC,所以AD=DE。
3. 等腰三角形的对顶角(顶点所对的两边的角)相等。
证明:在等腰三角形ABC中,已知∠B=∠C,∠BAC是三角形内角和,即∠BAC+∠CAB+∠ABC=180度,即2∠B+∠ABC=180度,解得∠ABC=180度-2∠B。
同理,∠ACB=180度-2∠C。
由于∠B=∠C,所以∠ABC=∠ACB。
因此,等腰三角形的对顶角相等。
二、等腰三角形的定理1. 等腰三角形底角的平分线是高和对称轴。

第一部分:知识点回顾角平分线的性质及判定:1、角平分线:把一个角平均分为两个相同的角的射线叫该角的平分线;2、角平分线的性质定理:角平分线上的点到角的两边的距离相等:①平分线上的点;②点到边的距离;3、角平分线的判定定理:到角的两边的距离相等的点在角平分线上。
4.注意在证明中用到这两个定理,如何把文字叙述转化成数学符号:例:如图角的平分线的性质定理的几何语言:∵OC是∠AOB的平分线,PD⊥OA于D,PE⊥OB于E,∴PD=PE角的平分线的判定定理的几何语言:∵PD⊥OA于D,PE⊥OB于E,PD=PE∴点P在∠AOB的平分线上等腰三角形的性质及判定:1.等腰三角形有两条边相等的三角形,叫做等腰三角形.相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.2.等腰三角形的性质和判定性质1 等腰三角形的两个底角相等(简写成“等边对等角”)性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“三线合一”)判定(1)有两条边相等的三角形,叫做等腰三角形(2)如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称为“等角对等边”)3.等边三角形三条边都相等的三角形叫做等边三角形.4.等边三角形的性质(1)等边三角形的三个内角都相等,并且每一个角都等于60°.(2)等边三角形是轴对称图形,共有三条对称轴.(3)等边三角形每边上的中线、高和该边所对内角的平分线互相重合.5.等边三角形有关判定(1 )三条边都相等的三角形是等边三角形(2)三个角都相等的三角形是等边三角形.(3)有一个角是60°的等腰三角形是等边三角形.6.由对等边三角形推出的一个关于直角三角形的一个性质在直角三角形中,如果有一个锐角等于30°,那么它对的直角边等于斜边的一半. 第二部分:典型例题如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于O,OB=OC。
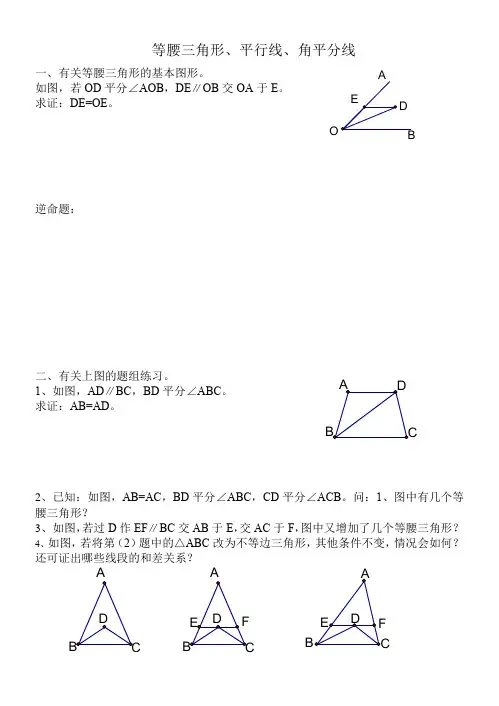
等腰三角形、平行线、角平分线一、有关等腰三角形的基本图形。
如图,若OD 平分∠AOB ,DE ∥OB 交OA 于E 。
求证:DE=OE 。
逆命题:二、有关上图的题组练习。
1、如图,AD ∥BC ,BD 平分∠ABC 。
求证:AB=AD 。
2、已知:如图,AB=AC ,BD 平分∠ABC ,CD 平分∠ACB 。
问:1、图中有几个等腰三角形?3、如图,若过D 作EF ∥BC 交AB 于E ,交AC 于F ,图中又增加了几个等腰三角形?4、如图,若将第(2)题中的△ABC 改为不等边三角形,其他条件不变,情况会如何?还可证出哪些线段的和差关系?O5、对第4题中“两内角平分线”可作怎样的推广?相应的线段和差关系如何?推广1当过△ABC 的一个内角和一个外角平分线的交点作这两角的公共边的平行线时,如图,EF=BE -CF推广2当过△ABC 的两个外角平分线上一点作这两个角的公共边的平行线时,如图,EF=AE+CF(5)如图,若BD ,CD 分别平分∠ABC 和∠ACB ,过D 作DE ∥AB 交BC 于E ,作DF ∥AC 交BC 于F 。
求证:BC 的长等于DEF 的周长。
6、把一张长方形纸条,像右图那样折叠,重合部分是什么形状?为什么?7、如图,△ABC 中,∠BAC=90,AB=AC ,AD ⊥BC 于D ,BE 平分∠ABC 交AD 于E ,AF 平分∠CAD 交DC 于F ,连结EF 。
指出图中的全等三角形、等腰三角形,并说明理由。
BF = 3.05 厘米m ∠FBD = 25.08︒m ∠DBC = 25.56︒m CB = 3.04 厘米。

角平分线和平行线出等腰例题角平分线和平行线出等腰例题角平分线和平行线是我们在几何学中经常遇到的概念。
它们是几何学中的基础知识,很多几何问题都离不开这两个概念。
在这篇文档中,我将讨论关于角平分线和平行线出等腰三角形的例题。
例题1:证明:如果一条角平分线与另一条边相交,那么这条角平分线将这个角分成两个相等的小角。
解析:首先,我们假设有一个角ABC,角平分线AD将其分成两个小角BAD和DAC。
我们需要证明角BAD等于角DAC。
根据角平分线的定义,角BAD和角DAC是由角ABC的两边所构成的。
我们可以将角BAD和角DAC的顶点放在一起,形成一个角BAC。
那么,角BAC的两条边AB和AC都是角ABC的边,这意味着角BAC等于角ABC。
然后,我们可以通过角相等的性质来得到结论。
角BAD等于角BAC,而角DAC等于角BAC,所以角BAD等于角DAC。
这样,我们就证明了角平分线将角ABC分成了两个相等的小角。
例题2:证明:如果一条平行线与一个角的两边相交,那么这条平行线将这个角分成两个相等的小角。
解析:给定一个角ABC和一条平行线DE,我们需要证明角ADE等于角BAC。
首先,我们可以通过转角的定义知道角ADE和角BAC 都是由角ABC的两条边所构成的。
我们将角ADE的顶点放在一起,形成一个角ABC。
由于平行线DE与角ABC的两边相交,可以知道平行线DE和线段AC构成了交角。
接下来,我们可以应用平行线的性质。
平行线与一条直线相交时,对应角相等。
所以,角ADE等于角ABC。
最后,我们可以通过角相等的性质得到结论。
角ADE 等于角ABC,而角BAC也等于角ABC,所以角ADE等于角BAC。
这样,我们就证明了平行线将角ABC分成了两个相等的小角。
例题3:证明:如果一条角平分线与一条平行线相交,那么这条平行线将角平分线所分的角分成两个相等的小角。
解析:给定一条角平分线AD和一条平行线BC,我们需要证明角BAD等于角DAC。

注意在证明中用到这两个定理,如何把文字叙述转化成数学符号:如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于O,OB=OC。
求证∠1=∠2.四边形ABCD中,AD∥BC,AE平分∠DAB,BE平分∠ABC,点E恰在DC上,∠C=∠D=90°。
(1)求证:AE⊥BE(2)猜想AB、AD、BC之间有何数量关系?请证明你的结论。
如图,D、E、F分别是△ABC的三条边上的点,CE=BF,△DCE和△DBF的面积相等.求证:AD平分∠BAC.如图,某铁路MN与公路PQ相交于点O,且夹角为90°,其仓库G在A区,到公路和铁路距离相等,且到公路距离为5cm.交BC于E,DBE所以这个三角形腰长为10㎝,底边长为7㎝。
剖析:在处理等腰三角形的问题时,有的同学习惯上总认为腰大于底,这是造成错误的原因所在。
事实上本题有两种情况。
正解:此题有两种情况:∵BD 为等腰△ABC 的中线∴AD=DC 设AB 为x ㎝ ,BC 为ycm.(1) ⎪⎪⎩⎪⎪⎨⎧=+=+122152y x x x 解得 ⎩⎨⎧==710y x 或 (2) ⎪⎪⎩⎪⎪⎨⎧=+=+152122y x x x 解得 ⎩⎨⎧==118y x 所以这个三角形腰长为10㎝,底边长为7㎝或腰长为8㎝,底边长为11㎝。
三、概念不清造成的错误例3、已知在等腰三角形中,一个角是另一个角的2 倍,求等腰三角形三个内角的度数。
错解:设等腰三角形的顶角为x°,则底角为2 x°。
根据题意,得 x+2x+2x=180解得 x=36 ∴2x=72∴这个等腰三角形的三个内角为:36°、72°、72°.剖析:错误在于误认为等腰三角形的底角一定大于顶角,是概念不清造成的错误想法。
本题应分底角大于或小于顶角两种情况解答。
正解:当等腰三角形的底角大于顶角时,设顶角为x°,则底角为2 x°。

第一部分:知识点回顾角平分线的性质及判定:1、角平分线:把一个角平均分为两个相同的角的射线叫该角的平分线;2、角平分线的性质定理:角平分线上的点到角的两边的距离相等:①平分线上的点;②点到边的距离;3、角平分线的判定定理:到角的两边的距离相等的点在角平分线上。
4.注意在证明中用到这两个定理,如何把文字叙述转化成数学符号:例:如图角的平分线的性质定理的几何语言:∵OC是∠AOB的平分线,PD⊥OA于D,PE⊥OB于E,∴PD=PE角的平分线的判定定理的几何语言:∵PD⊥OA于D,PE⊥OB于E,PD=PE∴点P在∠AOB的平分线上等腰三角形的性质及判定:1.等腰三角形有两条边相等的三角形,叫做等腰三角形.相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.2.等腰三角形的性质和判定性质1 等腰三角形的两个底角相等(简写成“等边对等角”)性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“三线合一”)判定(1)有两条边相等的三角形,叫做等腰三角形(2)如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称为“等角对等边”)3.等边三角形三条边都相等的三角形叫做等边三角形.4.等边三角形的性质(1)等边三角形的三个内角都相等,并且每一个角都等于60°.(2)等边三角形是轴对称图形,共有三条对称轴.(3)等边三角形每边上的中线、高和该边所对内角的平分线互相重合.5.等边三角形有关判定(1 )三条边都相等的三角形是等边三角形(2)三个角都相等的三角形是等边三角形.(3)有一个角是60°的等腰三角形是等边三角形.6.由对等边三角形推出的一个关于直角三角形的一个性质在直角三角形中,如果有一个锐角等于30°,那么它对的直角边等于斜边的一半. 第二部分:典型例题。


角平分线和平行线构成等腰三角形的探究-----李春蕊北京市育英学校一、教材分析:《等腰三角形》是“人教版八年级数学(上)”第十二章第三节的内容。
等腰三角形是一种特殊的三角形,它除了具备一般三角形的所有性质外,还有许多特殊的性质,由于这些特殊性质,使它比一般的三角形应用更广泛。
这一单元的主要内容是等腰三角形的性质和判定,以及等边三角形的相关知识,尤其是等腰三角形的性质和判定,它们是研究等边三角形、证明线段等和角等的重要依据.学情分析:本节课在学生已经学习了轴对称、等腰三角形性质及判定基础上,进一步探究角平分线和平行线形成等腰三角形的问题。
学生具有一定说理能力,整体几何感观比较清晰,在探究活动中,能够根据老师的问题进行有切入的思考。
二、教学目标:(1)掌握角平分线和平行线形成等腰三角形的基本规律;(2)体会研究问题中用到的分类思想,经历由特征图形问题的解决,发展对问题的进一步探究,认识到在几何问题中,位置关系可得出一定数量关系,特殊的数量关系也能推出一定位置关系.(3)通过交流和研讨,使学生在探索的同时获得解决问题的一种方法,提高学生学习数学的兴趣和信心.教学重点:掌握角平分线+平行线能形成等腰三角形这个基本规律,利用这个规律解决等腰三角形方面的有关问题.教学难点:灵活运用角平分线和平行线形成等腰三角形这个基本规律解决有关问题.突出重点方法:观察,思考,证明.突出难点方法:自主探究教学方法:启发与探究相结合教学准备:PPT,课本,作图工具三、教学设计:(一)复习等腰三角形相关知识1、请同学们对等腰三角形的知识要点进行自我回顾:(由学生先进行回顾,教师补充)(二)探究过程问题1:已知∠ABC,BD平分∠ABC,ED//BC.思考:△EBD是等腰三角形吗?解:是;EB=ED发现:无论点D 在BD 上如何运动,△EBD 都是等腰三角形结论:角平分线+平行线 等腰三角形我们在几何证明中,一般不单独研究角,大多数都是借助图形,比如在三角形中研究问题,上面问题如果放在三角形中,我们可以作三角形中一个角的角平分线,然后过角平分线上一点,作这个角的一边的平行线。
课 题 等腰三角形、角的平分线授课时间: 2013.备课时间:教学目标1. 熟练掌握等腰三角形、角的平分线的相关知识和性质。
教学内容(包括知识点、典型例题、课后作业)等腰三角形知识梳理一、等腰三角形的边角关系 1)判定定理 等角对等边 2)性质定理 等边对等角3)特殊角之间的关系 ∠B = ∠C=90°-21∠BAC∠BAC=180°-2∠B =180°-2∠C 4)底边BC 小于2倍的腰长AB 二、等腰三角形“三线”间的关系1)顶角的角平分线、底边上的中线、底边上的高(“三线合一”)2)等腰三角形两腰上的高相等、两腰上的中线相等、两底角的平分线相等; 三、等边三角形 1)概念2)性质 等边三角形具备所有等腰三角形的性质外还有: 三边都相等;三个内角都相等,且都等于60°;等边三角形是轴对称图形,有三条对称轴。
3)判定利用定义; 三个角都相等的三角形是等边三角形; 有一个角是60°的等腰三角形是等边三角形。
四、含30°的直角三角形1)定理 在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边的斜边的一半。
2)逆定理 在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的角等于30°五、等腰三角形的对称性等腰三角形是轴对称图形,有一条对称轴(底边的垂直平分线) 等边三角形有三条对称轴,即三边的垂直平分线。
复习巩固1、(2009•山西)如图,在Rt△ABC 中,∠ACB=90°,BC=3,AC=4,AB 的垂直平分线DE 交BC 的延长2线于点E,则CE 的长为 。
2、(2004•湖州)已知如图,在△ABC 中,BC=8,AB 的中垂线交BC 于D,AC 的中垂线交BC 与E,则△ADE 的周长等于 .3、(2010•娄底)如图,在四边形ABCD 中,AD∥BC,E 为CD 的中点,连接AE、BE,BE⊥AE,延长AE 交BC 的延长线于点F.求证:(1)FC=AD; (2)AB=BC+AD .典型例题 一.选择题1、已知等腰三角形的一个角等于42°,则它的底角为 ( ).A、42 °B、69°C、69°或84°D、42°或69°2、如图,ABC △中,AB AC ,30A ,DE 垂直平分AC ,则BCD 的度数为( ) A.80 B.75C.65 D.453、等腰三角形的顶角是80°,则一腰上的高与底边的夹角是( )A.40° B.50° C.60° D.30°4. 如图,15A ∠,AB BC CD DE EF ,则DEF ∠等于( )A .90 B.75 C.70 D.60A B D EC5、如图,△MNP中, ∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是( )PQMNGA.8+2a B.8+a C.6+a D.6+2a二.选择题1. 在△ABC 中,AB=AC,若∠B=56º,则∠C=__________.2.等腰三角形底边中点与一腰的距离为6,则腰上的高为______.3.如图,在△ABC 中,AB=AC,CD 平分∠ACB 交AB 于点D,AE∥DC 交BC 的延长线于点E,已知∠E=36°,则∠B= .4.如图,在ABC △中,点D 是BC 上一点,80BAD °,AB AD DC ,则C .三.解答题1. 下午2时,一轮船从A 处出发,以每小时40海里的速度向正南方向行驶,下午4时,到达B 处,在A 处测得灯塔C 在东南方向,在B 处测得灯塔C 在正东方向,在图中画出示意图 ,并求出B、C 之间的距离.2. 如图,在四边形ABCD 中,AB=AD,CB=CD,求证:∠ABC=∠ADC.AC B D804DCAB加强巩固角的平分线DCAEB一、知识准备: 1)角的平分线的画法2)角的平分线的性质: 。
龙源期刊网 例谈角平分线、平行线、等腰三角形三者关系
作者:杨斌
来源:《数学大世界·中旬刊》2019年第12期
在几何教学中,我们常常会发现图形之间并非孤立的,而是你中有我,我中有你的一种感觉,有时甚至有“我的世界离不开你”的共生共存的依恋之情。
而让我们的学生真正能读懂复杂图形中隐含的这种关系,着实是一项必须训练的思维和能力,同时对数学成绩提高有很大的帮助作用。
下面我们从人教新版初中数學八年级上册82页一道课本练习题说起,例谈角平分线、平行线、等腰三角形三者之间的关系。
一、模型来源。
等腰直角三角形的角平分线等腰直角三角形的角平分线,听起来有点复杂,但其实它就像一场数学的舞蹈,简单而优雅。
想象一下,一个等腰直角三角形,两个边一样长,90度的角像个热情洋溢的舞者,随时准备炫舞。
你看,这个三角形就像是它的名字一样,左边和右边都很对称,真是个小可爱。
我们这里不讨论深奥的理论,咱们聊聊这个角平分线。
这个角平分线就像是一条隐秘的小路,悄悄地把这个90度的角一分为二。
你可以把它想象成一位温柔的调解者,把两边的冲突化解掉,嘿嘿,真是太贴心了。
它的存在让整个三角形看起来更和谐,仿佛在说“兄弟,咱们别打架,一起舞蹈吧!”角平分线的长度也是个迷人话题。
它不单单是简单的线段,还是通往另一个世界的桥梁。
没错,它让三角形里的每一寸空间都充满了可能性,神秘而又迷人。
说到角平分线的性质,那简直是一颗璀璨的宝石。
它不仅把角分成两半,还把对面的边分成了成比例的部分。
哇,这可真是太酷了!就像是在帮我们拿到超能力,给每一位舞者留出足够的空间来展现自己的风采。
你是不是想到了“公正”的概念?没错,角平分线就是这个概念的化身,它告诉我们在这个数学世界里,公平和和谐是多么重要。
再想象一下,如果没有这个角平分线,整个三角形就像是个不知所措的孩子,四处乱撞。
可是,有了这个线段,所有的混乱都被它妥善地整理好了。
就像在一个热闹的派对上,总会有一个人负责把大家的饮料分好,这样大家才能愉快地聊天。
角平分线也在这个三角形的派对上做着同样的事情,默默无闻,却至关重要。
玩转角平分线不仅仅是欣赏它的美丽,还要学会如何计算它的长度。
简单来说,使用勾股定理就能轻松搞定。
不知道你有没有感觉,数学有时候就像一把钥匙,打开了一个又一个神秘的门。
勾股定理就像那个让人兴奋的密码,一旦掌握,就能让你进入角平分线的秘密世界,真是让人忍不住想要大喊“太好了!”等腰直角三角形的角平分线还有一个特别的性质,那就是它的长度正好等于其他两条边的一半,简直就是一颗闪亮的星星在数学的天空中熠熠生辉。
如何求解等腰三角形的底边等腰三角形是指两条边的长度相等的三角形,底边则是等腰三角形中较长的一条边。
在解题过程中,我们可以利用等腰三角形的特性和一些几何定理来求解底边的长度。
本文将介绍两种常见的方法,一种是利用勾股定理,另一种是利用角平分线及正弦定理。
方法一:利用勾股定理勾股定理是一个描述直角三角形边长关系的定理,根据勾股定理可以得出如下关系式:c²= a²+ b²(其中c为斜边的长度,a、b分别为两条直角边的长度)对于等腰三角形,两条边的长度相等,假设等腰三角形的两条等边分别为a,底边的长度为b。
我们可以将其中的一条等边作为直角边,然后利用勾股定理来求解底边的长度。
设等边长度为a,底边长度为b,则有:b² = (a/2)² + a²化简上述等式,可得:b² = a²/4 + a²b² = (5a²)/4通过开方操作,可以得到等腰三角形的底边长度:b = √((5a²)/4)方法二:利用角平分线及正弦定理角平分线是指将一个角平分为两等分角的直线,利用角平分线可以求解等腰三角形的底边长度。
同时,我们也可以利用正弦定理来辅助求解。
假设等腰三角形的两条等边分别为a,底边的长度为b。
设角平分线与底边的交点为E,将角平分线分为两段,分别为DE和EF。
利用正弦定理,可以得到如下关系式:a/sin(A/2) = b/sin(A)其中A为顶角的度数。
由于等腰三角形的两个底角相等,所以角A/2和角A也相等,可以简化上述关系式:a/sin(A/2) = b/sin(A/2)进一步化简,可以得到:b = a所以,等腰三角形的底边长度等于其两条等边的长度。
综上所述,我们介绍了两种求解等腰三角形底边长度的方法。
根据题目要求,我们不再赘述标题和其他内容,通过上述叙述,您可以清楚地了解如何求解等腰三角形的底边长度。
角平分线与等腰三角形
江苏 刘顿
角平分线与等腰三角形有着密不可分联系.在许多几何问题中,遇到等腰三角形就会想到顶角的平分线,遇到角平分线又会想到构造等腰三角形.为了能说明这个问题,下面归类说明.
一、角平分线+平行线→等腰三角形
当一个三角形中出现角平分线和平行线时,我们就可以寻找到等腰三角形.如图1①中,若AD 平分∠BAC ,AD ∥EC ,则△ACE 是等腰三角形;如图1②中,AD 平分∠BAC ,DE ∥AC ,则△ADE 是等腰三角形;如图1③中,AD 平分∠BAC ,CE ∥AB ,则△ACE 是等腰三角形;如图1④中,AD 平分∠BAC ,EF ∥AD ,则△AGE 是等腰三角形.
例1 如图2,△ABC 中,AB =AC ,在AC 上取点P ,过点P 作EF ⊥BC ,交BA 的延长线于点E ,垂足为点F .求证:AE =AP .
简析 要证AE =AP ,可寻找一条角平分线与EF 平行,于是想到AB =AC ,则可以作AD 平分∠BAC ,所以AD ⊥BC ,而EF ⊥BC ,所以AD ∥EF ,所以可得到△AEP 是等腰三角
形,故AE =AP .
例2 如图
3,在△ABC 中,∠BAC ,∠BCA 的平分线相交于点O ,过点O 作DE ∥
AC ,分别交AB
,BC 于点D ,E .试猜想线段AD ,CE ,DE 的数量关系,并说明你的猜想理由. 简析 猜想:
AD +CE =DE .理由如下:由于OA ,OC 分别是∠BAC ,∠BCA 的平分线,DE ∥AC ,所以△ADO 和△CEO 均是等腰三角形,则DO =DA ,EC =EO ,故AD +CE =DE . 例3 如图4,△ABC 中,AD 平分∠BAC ,E ,F 分别在BD ,AD 上,且DE =CD ,EF =AC .求证:EF ∥AB .
简析 由于这里要证明的是EF ∥AB ,而AD 平分∠BAC ,所以必须通过辅助线构造出平行线,这样就可以得到等腰三角形了,于是DE =CD 的提示下,相当于倍长中线,即延长AD 至M ,使DM =AD ,连结EM ,则可证得△MDE ≌△ADC ,所以ME =AC ,又EF =AC ,∠M =∠CAD ,所以∠M =∠EFM ,即∠CAD =∠EFM ,又因为AD 平分∠BAC ,所以∠BAD =∠EFD =∠CAD ,所以EF ∥AB .
二、角平分线+垂线→等腰三角形
当一个三角形中出现角平分线和垂线时,我们就可以寻找到等腰三角形.如图5中,若C A B E D O
图3 图4 F C D E B A M 图2
F B A C D P E 图1
① D ② C D C ④
F C D
AD 平分∠BAC ,AD ⊥DC ,则△AEC 是等腰三角形.
例4 如图6,已知等腰R t△ABC 中,AB =AC ,∠BAC =90°,BF 平分∠ABC ,CD ⊥BD 交BF 的延长线于D .求证:BF =2CD .
简析 由BF 平分∠ABC ,CD ⊥BD ,并在图5的揭示之下,延长线BA ,CD 交于点E ,于是△BCE 是等腰三角形,并有ED =CD ,余下来的问题只需证明BF =CE ,而事实上,由∠BAC =90°,CD ⊥BD ,∠AFB =∠DFC ,得∠ABF =∠DCF ,而AB =AC ,所以△ABF ≌△ACE ,则BF =CE ,故BF =2CD .
三、作倍角的平分线→等腰三角形
当一个三角形中出现一个角是另一个角的2倍时,我们就可以作倍角的平分线寻找到等腰三角形.如图7中,若∠ABC =2∠C ,如果作BD 平分∠ABC ,则△DBC 是等腰三角形.
例5 如图8,△ABC 中,∠ACB =2∠B ,BC =2AC .求证:∠A =90°.
简析 由于条件中有两个倍半关系,而结论与角有关,因此首先考虑对∠ACB =2∠B 进行技术处理,即作CD 平分∠ACB 交AB 于D ,过D 作DE ⊥BC 于E ,则由∠ACB =2∠B 知∠B =∠BCD ,即△DBC 是等腰三角形,而DE ⊥BC ,所以BC =2CE ,又BC =2AC ,所以AC =EC ,所以易证得△ACD ≌△ECD ,所以∠A =∠DEC =90°.
E 图5 A
B C D 图6 B F D
E C A 图7 B C D A E 图8 C B A D。