三角形内外角平分线有关命题的证明及应用
- 格式:doc
- 大小:80.00 KB
- 文档页数:7

三角形角平分线8大结论的证明三角形的角平分线,这个话题一听就有点儿数学范儿对吧?不过别着急,今天我们就轻松聊聊这8个有趣的结论,说不定你会发现,原来三角形的角平分线竟然那么有意思,甚至可以用来解一些生活中的“小难题”呢!行了,不废话,直接进入正题,看看三角形的角平分线到底能带来什么样的神奇“魔力”。
大家应该知道,角平分线就是把三角形的一个角一分为二的那条线。
你要是把三角形的一个角想象成一个蛋糕,这个角平分线就像是把蛋糕均匀切开的刀。
看着简单吧?但是它的性质可不简单哦!你可以想象它就像三角形的“魔法杖”,有很多奇妙的地方。
第一个结论:角平分线把对边分成的两部分,比例跟两条邻边的比例是一样的。
说白了,如果你把角平分线看作一根“弓箭”,它射出的箭就是把对面的边分成的两个小段,它们的长度就像两个有着特殊关系的小伙伴,一起玩耍的时间都不多,比例一样,心照不宣。
具体来说,如果你有一个角,角平分线把对边分成了两段,那这两段的长度,就跟角平分线两边的邻边长度有个固定的比例关系。
怎么样,神奇吧?第二个结论:角平分线定理,真的是生活中的“逆天”法宝。
假设你在做一道几何题,发现角平分线正好把三角形对边分成了两个长度不等的部分,这时候你就可以运用这个定理,迅速求出两段长度的比例了,反正你心里有个定心丸。
别看它简单,这个定理其实给你解题省了不少功夫。
然后,第三个结论来了:如果三角形的角平分线穿过了对边的一点,那你就可以通过这个点找到更多的“线索”。
这就像是破案时发现了新的线索,揭开了谜底的那一刻。
通过这个点的角平分线,可以得出三角形的某些特殊关系,比如说三角形的面积、角度等等,简直就是几何学的小秘密!接着看,第四个结论是:如果三角形的三个角平分线交于一点,这个点就叫做“三角形的内心”。
哦,对了,这个内心叫做“内心点”,意思是说,无论三角形多么古怪,这三条角平分线交汇的地方就能“告诉”你整个三角形的心脏在哪儿。
这也就意味着,三角形的内心是它的“平衡点”,一种几何的“核心”!第五个结论,也是个挺酷的:角平分线可以用来求三角形的面积。

三角形角平分线的三个定理证明今天我们来聊聊三角形的角平分线,不知道大家有没有听过这个名字?别着急,别皱眉头,咱们今天就用轻松的方式聊聊它的三个定理。
嗯,对了,别一听到“定理”就想着这些东西都很难。
其实说白了,就是一些数学小规律,咱们捋顺了,分分钟能掌握!三角形的角平分线,就好比一个人站在三角形的顶点,把顶点的角一分为二,这两部分就叫做“角平分线”。
所以说,角平分线其实就是把角给“平分”了。
就像咱们吃饭的时候,大家都吃的差不多,没谁吃得特别多,也没谁吃得特别少,吃到最后大家都差不多,能吃个七八分饱。
这就是角平分线的第一步,它把角“分得很均匀”。
好啦,咱们先来看看第一个定理——角平分线定理。
这个定理说的是:在一个三角形里,如果你把其中一个角分成两个相等的角,那么角平分线就会把对边分成两段,比例就和另外两个边的长度成正比。
说起来可能有点绕,不过理解一下其实很简单。
比如说你有一个三角形,角A被角平分线分成了两个相等的角,接着角平分线碰到了对边BC,这时候,角平分线把对边BC分成了两段——一段叫做BD,一段叫做DC。
于是,BD和DC的比例就跟AB和AC的比例一样。
所以,简单来说,角平分线把对边分得“恰如其分”,好像是两个好朋友,他们不争不抢,分得刚刚好。
怎么说呢?简直就是“分蛋糕分得不多不少”。
这个定理,其实很直白,理解起来就像你吃一块蛋糕,吃到自己的一块,剩下的也给大家分得差不多,公平又公正。
接下来我们来说第二个定理,角平分线的外角定理。
听着名字可能有点“高大上”,但说白了就是,三角形外面的某些角也能有它的分法。
这里的关键点是,三角形的一条角平分线延伸到外面,它和外面的对边之间有一个特殊的关系。
你看,假如角平分线从角A出发,穿过三角形的外边,这时候,外面这个角的大小恰好等于它与角平分线的内角的加和的一半。
也就是说,它跟内部的角平分线内外的配合得当,像是一对搭档,互相配合,默契十足。
所以,这个定理就像我们常说的“知己知彼,百战不殆”,内外呼应,整体协作,效果好到飞起。

三角形的角平分线定理解析三角形的角平分线定理是指:三角形内任意一条角的角平分线,都能将该角分成两个相等的角。
这个定理在解决三角形相关问题时非常有用,可以帮助我们推导出一些重要的结论和性质。
接下来,我们将对三角形的角平分线定理进行详细的解析。
一、角平分线的定义在三角形ABC中,假设角A的角平分线与边BC相交于点D,那么我们可以称线段AD为角A的角平分线。
角平分线的作用是将角A 分成两个相等的角BAD和CAD。
二、角平分线定理的几何解析根据角平分线的定义,我们可以得出以下几何结论:1. 任意角的角平分线两端的线段长度相等。
即AD = CD。
证明:作BD与AC的延长线交于点E。
由于△ABD和△CAD中有AD = AD(公共边)、∠BAD = ∠CAD(角平分线的定义)和∠BDA = ∠CDA(共同内角),所以根据ASA(边角边)的性质可以得出△ABD ≌△CAD。
因此,AD = CD。
2. 角平分线将对边分成两个与角平分线所在边等长的线段。
即BD = CD。
证明:由于△ABD和△ACD中有∠BDA = ∠CDA(共同的内角),∠ABD = ∠ACD(角平分线的定义)和AD = AD(公共边),根据ASA(角边角)的性质可以得出△ABD ≌△ACD。
因此,BD = CD。
三、角平分线定理的应用角平分线定理不仅可以帮助我们推导出一些证明,还可以在解题过程中起到积极的作用。
下面我们通过一些例子来说明角平分线定理的应用。
例子1:给定三角形ABC,角BAD是角A的角平分线,若∠BAD = 60°,求∠ACB的度数。
解:由角平分线定理可知BD = CD,且∠BAD = ∠CAD = 60°。
由于∠BAD + ∠CAD + ∠ACB = 180°(三角形内角和定理),代入已知信息可得60° + 60° + ∠ACB = 180°,解得∠ACB = 60°。

三角形内外角平分线一.命题的证明及应用在中考常有与三角形内外角平分线有关的题目,若平时不注意总结是很难一下子解决的.下面来一起学习一下.命题1 如图1,点D是△ABC两个内角平分线的交点,则∠D=90°+∠A.证明:如图1:∵∠1=∠,∠2=∠,∴2∠1+2∠2+∠A=180°①∠1+∠2+∠D=180°②①-②得:∠1+∠2+∠A=∠D③由②得:∠1+∠2=180°-∠D④把③代入④得:∴180°-∠D+∠A=∠D∠D=90°+∠A.点评利用角平分线的定义和三角形的内角和等于180°,不难证明.命题2 如图2,点D是△ABC两个内角平分线的交点,则∠D=90°-∠A.证明:如图2:∵DB和DC是△ABC的两条外角平分线,∴∠D=180°-∠1-∠2=180°-(∠DBE+∠DCF)=180°-(∠A+∠4+∠A+∠3)=180°-(∠A+180°)=180°-∠A-90°=90°-∠A;点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和以及三角形的内角和等于180°,可以证明.命题3 如图3,点E是△ABC一个内角平分线与一个外角平分线的交点,则∠E=∠A.证明:如图3:∵∠1=∠2,∠3=∠4,∠A+2∠1=2∠4①∠1+∠E=∠4②①×代入②得:∠E=∠A.点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和,很容易证明.命题4如图4,点E是△ABC一个内角平分线BE与一个外角平分线CE 的交点,证明:AE是△ABC的外角平分线.证明:如图3:∵BE是∠ABC的平分线,可得:EH=EFCE是∠ACD的平分线, 可得:EG=EF∴过点E分别向AB、AC、BC所在的直线引垂线,所得的垂线段相等.即EF=EG=EH∵EG=EH∴AE是△ABC的外角平分线.点评利用角平分线的性质和判定能够证明.应用上面的结论能轻松地解答一些相关的比较复杂的问题,下面来一起看.例1如图5,PB和PC是△ABC的两条外角平分线.①已知∠A=60°,请直接写出∠P的度数.②三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形?解析:①由命题2的结论直接得:∠P=90°-∠A=90°-×60°=60°②根据命题2的结论∠P=90°-∠A,知三角形的三条外角平分线所在的直线形成的三角形的三个角都是锐角,则该三角形是锐角三角形.点评此题直接运用命题2的结论很简单.同时要知道三角形按角分为锐角三角形、直角三角形和钝角三角形.例2如图6,在△ABC中,延长BC到D,∠ABC与∠ACD的角平分线相较于点,∠BC与∠CD 的平分线交与点,以此类推,…,若∠A=96°,则∠= 度.解析:由命题③的结论不难发现规律∠∠A .可以直接得:∠=×96°=3°.点评 此题是要找出规律的但对要有命题③的结论作为基础知识.例3(203陕西第一大题填空题第八小题,此题3分)如图7,△ABC 的外角∠ACD 的平分线CP 的内角∠ABC 平分线BP 交于点P ,若∠BPC=40°,则∠CAP=_______________.解析:此题直接运用命题4的结论可以知道AP是△ABC 的一个外角平分线,结合命题3的结论知道∠BAC=2∠BPC, CAP=(180°-∠BAC )= (180°-2∠BPC )=50°.点评 对命题3、4研究过的读者此题不难,否则将是一道在考试的时候花时间也不一定做的出来的题目. 例4 (2003年山东省)如图,在Rt △ABC 中,∠ACB=90°,∠BAC=30°,∠ACB 的平分线与∠ABC 的外角平分线交与E 点,连接AE ,则∠AEB= 度.解析:有题目和命题4的结论可以知道AE 是△ABC 的一个外角平分线, 结合命题2的结论知道∠AEB=∠ACB -∠ACB=90°-×90°=45°点评 从上面的做题过程来看题目中给出的“∠A=30°”这个条件是可以不用的.二.角平分线定理使用中的几种辅助线作法一、已知角平分线,构造三角形例题、如图所示,在△ABC 中,∠ABC=3∠C ,AD 是∠BAC 的平分线,BE ⊥AD 于F 。

角平分线定理2证明角平分线定理2是指在一个三角形中,如果一个角的平分线上某个点到另外两边的距离比另外一个点到两边的距离大,则该角的平分线所对应的两个小角的角平分线也相应地实现这个条件。
下面我们来证明这个定理。
设在三角形ABC中,点D和E分别是角BAC的平分线上的两个点,且满足AD > AE;点F和G分别是角BAC的平分线所对应的两个小角的角平分线上的两个点。
首先,连接BD、BE、CD、CE、AF和AG。
要证明FG是角BAC的平分线所对应的两个小角的角平分线,我们需要证明FG与AB和AC平分的两个小角分别相等。
根据角平分线的定义,我们可以得到以下等式:∠BDA = ∠ADE∠CDA = ∠AED∠CGA = ∠AGE∠CFA = ∠AFE接下来,我们要使用一些三角形的性质,来推导出角BFG和角BAG的等式,以及角CGF和角CAF的等式。
由于∠BDA = ∠ADE,且∠DEA是角DAE的平分线,根据角BDA和角ADE平分线定理,我们可以得到:∠BDA = ∠EDA由于∠CGA = ∠AGE,且∠AGE是角AEG的平分线,根据角CGA和角AGE平分线定理,我们可以得到:∠CGA = ∠EGA同样地,由于∠CFA = ∠AFE,且∠AFE是角AEF的平分线,根据角CFA和角AFE平分线定理,我们可以得到:∠CFA = ∠EFA再由于∠BFD = ∠DFA,且∠BFD是角BDF的平分线,根据角BFD和角DFA平分线定理,我们可以得到:∠BFD = ∠AFD类似地,由于∠CGE = ∠EGA,且∠CGE是角CTE的平分线,根据角CGE和角EGA平分线定理,我们可以得到:∠CGE = ∠AGE最后,由于∠CFE = ∠EFA,且∠CFE是角CEF的平分线,根据角CFE和角EFA平分线定理,我们可以得到:∠CFE = ∠AFE综上所述,我们可以得出以下结论:∠BDA = ∠EDA∠CGA = ∠EGA∠CFA = ∠EFA∠BFD = ∠AFD∠CGE = ∠AGE∠CFE = ∠AFE因此,根据角等于其对应的平分线所对应的两个小角之和的性质,我们可以得到:∠BDF + ∠BFD = ∠ADF∠CGE + ∠EGA = ∠CGA∠CFE + ∠EFA = ∠CFA进一步地,我们可以得到:∠BDF + ∠AFD = ∠ADF∠CGE + ∠AGE = ∠CGA∠CFE + ∠AFE = ∠CFA由于∠BDF = ∠AGE,∠AFD = ∠CGA,以及∠EFA =∠CFA,我们可以得到:∠ADF = ∠CGA∠CGA = ∠CFA从而可以得出结论:FG是角BAC的平分线所对应的两个小角的角平分线。

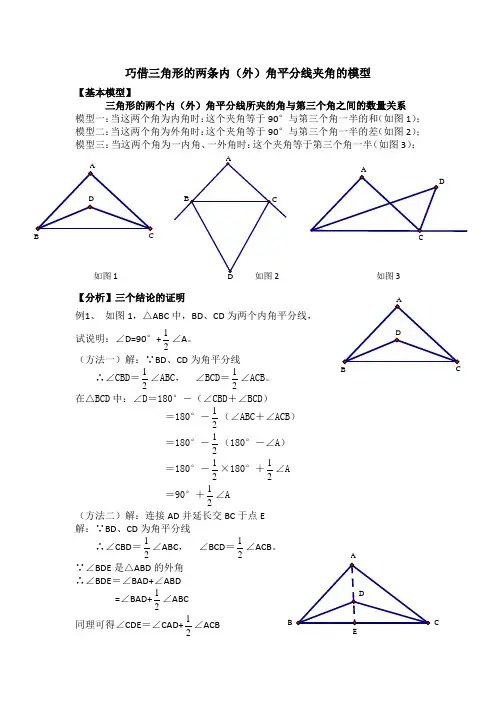
BBECB A巧借三角形的两条内(外)角平分线夹角的模型【基本模型】三角形的两个内(外)角平分线所夹的角与第三个角之间的数量关系 模型一:当这两个角为内角时:这个夹角等于90°与第三个角一半的和(如图1); 模型二:当这两个角为外角时:这个夹角等于90°与第三个角一半的差(如图2); 模型三:当这两个角为一内角、一外角时:这个夹角等于第三个角一半(如图3);【分析】三个结论的证明例1、 如图1,△ABC 中,BD 、CD 为两个内角平分线,试说明:∠D=90°+21∠A 。
(方法一)解:∵BD 、CD 为角平分线∴∠CBD =21∠ABC , ∠BCD =21∠ACB 。
在△BCD 中:∠D =180°-(∠CBD +∠BCD )=180°-21(∠ABC +∠ACB )=180°-21(180°-∠A )=180°-21×180°+21∠A=90°+21∠A(方法二)解:连接AD 并延长交BC 于点E 解:∵BD 、CD 为角平分线∴∠CBD =21∠ABC , ∠BCD =21∠ACB 。
∵∠BDE 是△ABD 的外角 ∴∠BDE =∠BAD+∠ABD=∠BAD+21∠ABC同理可得∠CDE =∠CAD+21∠ACB又∵∠BDC =∠BDE+∠CDE∴∠BDC =∠BAD+21∠ABC+∠CAD+21∠ACB=∠BAC+21(∠ABC+∠ACB )=∠BAC+21(180°-∠BAC )=90°+21∠BAC例2、如图,BD、CD为△ABC的两条外角平分线,试说明:∠D=90°-21∠A 。
解:∵BD 、CD 为角平分线∴∠CBD=21∠CBE∠BCD =21∠BCF又∵∠CBE 、∠BCD 为△ABC 的外角 ∴∠CBE =∠A +∠ACB ∠BCF =∠A +∠ABC∴∠CBE +∠BCF =∠A +∠ACB +∠A +∠ABC =∠A +180°在△BCD 中:∠D =180°-(∠CBD +∠BCD )=180°-(21∠CBE +21∠BCF )=180°-21(∠CBE +∠BCF )=180°-21(∠A +180°)=90°-21∠A【小结】通过对模型1、2的分析和证明,我们还能发现三角形两内角平分线的夹角和两外角平分线的夹角互补,即和为180°。

三角形内角平分线的性质定理的证明本文介绍的是三角形内角平分线的性质定理及其证明。
该定理可以分为两个部分,即三角形内角平分线分对边为两部分,且这两部分与两邻边成比例。
现在我们将介绍四种不同的证明方法。
方法一:利用平行线作等比代换。
我们作DE//BC,DE交AC于点E。
根据已知条件∠1=∠2,我们可以得到∠2=∠3.同时,由平行线的性质可知DE=EC。
因此,我们可以得到AD/AC=DE/EC=BD/BC,即AD/BD=AC/BC。
方法二:应用平行线分线段成比例定理,等比代换中辅以等量代换。
我们作BE//DC,BE交AC的延长线于点E。
根据已知条件∠1=∠2,我们可以得到∠2=∠3.同时,由平行线的性质可知BC=CE。
因此,我们可以得到AD/AC=AE/CE=BD/BC,即AD/BD=AC/BC。
方法三:进行逆推分析。
我们可以在AC的延长线上作一个CE=BC,然后连接BE。
由于∠2=∠ACB,我们可以得到∠3=∠E。
因此,BE//DC,从而可以得到AD/AC=AE/CE=BD/BC,即AD/BD=AC/BC。
方法四:改变三角形的内角大小。
我们可以改变△ADC 的一个内角的大小,把它改造为△AEC,使之与△XXX相似并作等量代换。
在∠CAB的同侧,作∠CAE=∠B,AE与CD 的延长线交于点E。
由于∠1=∠2,我们可以得到△ACE∽△BCD。
因此,我们可以得到AD/AC=AE/CE=BD/BC,即AD/BD=AC/BC。
以上是四种不同的证明方法,它们都可以证明三角形内角平分线分对边为两部分,且这两部分与两邻边成比例的性质定理。

一内一外角平分线模型证明过程一、引言一内一外角平分线模型是几何学中的一个重要概念,它可以帮助我们理解角平分线的性质和应用。
本文将以一内一外角平分线模型为基础,通过证明过程来展示其应用和推导过程。
二、一内角平分线的性质我们来看一内角平分线的性质。
在三角形ABC中,假设AD是角BAC的内角平分线。
根据角平分线的定义,角BAD和角CAD是等角。
我们可以证明以下性质:1. AD与BC垂直为了证明AD与BC垂直,我们需要利用角度的性质。
根据等角的定义,我们可以得到∠BAD = ∠CAD。
又因为∠BAC = 2∠BAD,所以∠BAC = 2∠CAD。
根据角度的和等于180度,我们可以得到∠BAC + ∠CAD = 180度。
由于∠BAC和∠CAD是等角,所以它们的和等于180度的一半,即90度。
因此,AD与BC垂直。
2. AD平分角BAC为了证明AD平分角BAC,我们可以利用角度的性质。
根据等角的定义,我们可以得到∠BAD = ∠CAD。
又因为∠BAC = 2∠BAD,所以∠BAC = 2∠CAD。
根据角度的和等于180度,我们可以得到∠BAC + ∠CAD = 180度。
由于∠BAC和∠CAD是等角,所以它们的和等于180度的一半,即90度。
因此,AD平分角BAC。
三、一外角平分线的性质接下来,我们来看一外角平分线的性质。
在三角形ABC中,假设AE是角BAC的外角平分线。
根据角平分线的定义,角BAE和角CAE是等角。
我们可以证明以下性质:1. AE与BC垂直为了证明AE与BC垂直,我们需要利用角度的性质。
根据等角的定义,我们可以得到∠BAE = ∠CAE。
又因为∠BAC = ∠BAE + ∠CAE,所以∠BAC = 2∠BAE。
根据角度的和等于180度,我们可以得到∠BAC + ∠BAE = 180度。
由于∠BAC和∠BAE是等角,所以它们的和等于180度的一半,即90度。
因此,AE与BC垂直。
2. AE平分角BAC的补角为了证明AE平分角BAC的补角,我们可以利用角度的性质。

有关三角形角平分线的有趣问题的讨论前言:角平分线这个词我们并不陌生,初中时,我们便知道等腰三角形两底角的平分线相等、全等三角形对应角平分线相等的一些有关三角形角平分线的定理,今天就让我们更加深入的探究角平分线的特性吧!正文:一.斯坦纳—雷米欧司定理尽然我们知道“等腰三角形两底角的平分线相等”是一个真命题,那么我们便可以猜想:它的逆命题是否也是真命题呢?也就是“有两条内角平分线相等的三角形是等腰三角形”是否成立?在两千多年前,欧几里得在他的经典巨著《几何原本》中便给出了上述第一个命题的证明,但是他却没有能够证明第二个命题也就是第一个命题的逆命题.直到十八世纪,雷米欧司重新提出这个题目,著名的德国几何学家斯坦纳才给出了这个逆命题的证明.所以,现在大家都把它叫“做斯坦纳—雷米欧司定理”既然连欧几里得也无法证明的命题,我们中学生该如何下手呢?自然地,我们便想到要不从最简单的方式入手吧?①反证法:我们先将命题化为几何语言:如图,已知BP、CQ分别是△ABC的内角∠ABC、∠ACB的平分线,且BP=CQ 求证:△ABC是等腰三角形证明:如上图,设∠ABP=∠PBC=½∠ABC=β,∠ACQ=∠QCB=½∠ACB=α设BP与CQ交点为O(这样要证明△ABC为等腰三角形便要转换为证明α=β)若α>β,于是在线段OP上可以取一点R使∠RCD=β且BR<BP在△BQC与△CRB中∵∠BQC=180°-(2β+α),∠CRB=180°-(2β+α)∴∠BQC=∠CRB又∵α>β∴∠QBC<∠RCB根据正弦定理 BR =Sin∠RCB > Sin∠QBC =CQBC Sin∠CRB Sin∠BQC BC∴BR>CQ=BP 这与BR<BP矛盾故α>β不成立同理可证α<β也不成立∴α只能与β相等∴∠ABC=∠ACB∴△ABC为等腰三角形同学们是否感觉到用反证法证明很容易呢?其实,斯坦纳一开始也是用反证法证明的,但他的方法比我们的方法更烦琐些,命题已经证完了,大家终于可以松一口气了,但是我们知道,反正法毕竟不能取代纯几何证法,纯几何证法才是能够使几何命题完善的.在斯坦纳证明该命题后,就陆续有数学爱好者提出了其他证明方法,海塞便是其中之一?②纯几何证法——海塞证法(在这里,已知、求证便不再写出)证明:在△BDC的外侧作∠BDF=∠ECB且使得DF=BC 连接BF在△BDF与△ECB{BD=EC ∠BDF=∠ECB DF=CB}∴△BDF≌△ECB ∴BF=EB ,∠FBD=∠BEC设∠ABD=α=∠DBC, ∠ACE=β=∠BCE则∠FBC=∠FBD+∠DBC=∠BEC+∠DBC=180°-(2α+β) +α=180°-(α+β)∠FDC=∠FDB+∠BDC=β+180°-(2β+α)=180°-(α+β)∴∠FBC=∠FDC∵2α+2β<180 ∴α+β<90°∴180°-(α+β) >90°即∠FBC=∠FDC>90°过点C作BF的垂线交FB延长线G,过点F作DC的垂线交CD 延长线于点H∴∠CBG=180°-∠FBC=180°-∠CDF=∠FDH又∵∠CGB=∠FHD=90°,BC=DF∴△CGB≌△FHD ∴FH=CG ,HD=GB连接CF ∵CF=FC ,FH=CG∴Rt△FCH≌Rt△CFG(HL)∴CH=FG∴CH-HD=FG-GB即CD=FB又∵BF=EB ∴CD=BE又∵EC=BD ,BC=BC∴△EBC≌△DCB∴∠EBC=∠DCB 即∠ABC=∠ACB ∴△ABC是等腰三角形二.角平分线定理说起角平分线,大家一定能想到:角平分线所联系的一些线段是否存在某种关系?比如:比例关系?下面我向大家介绍内角平分线定理与外角平分线定理【1】内角平分线定理已知:AD为△ABC的一条内角平分线求证:BD/CD=AB/AC①利用正弦定理证明AB= Sin∠ADB = Sin∠ADC =ACBD Sin∠BAD Sin∠CAD DC∴AB=BDAC DC②利用辅助线如图,过点C作CE∥DA交BA延长线于点E 则∠AEC=∠BAD , ∠ACE=∠DAC ∵∠BAD=∠DAC ∴∠AEC=∠ACE∴AE=AC∵AD∥EC ∴AB=BD ∴AB = BDAE DC AC DCPS:这个定理其实有很多种证法,这里只是列举了最简单的两种【2】外角平分线定理已知:如图,△ABC的外角∠ACE的平分线CD与BA的延长线交于点D求证:BC=BDAC AD证明:(面积法)在BC延长线上取点E使CE=AC在△ACD与△ECD中∵{AC=EC ∠ACD=∠ECD CD=CD }∴△ACD≌△ECD ∴S△ACD= S△ECD AC=CE∴BC = BC = S△BCD = S△BCD = BDAC CE S△DCE S△ACD AD(这里用了同高三角形的面积之比等于其对应底边之比)PS:这个定理也有很多证法,此证明为我原创竟然我们已经证明了角平分线所联系的一些线段存在比例关系,那么我们是否可以进一步完成角平分线的长度是否与这些线段有关呢?下面我们便来探索角平分线的长度定理三.Schooten定理Schooten定理是平面几何最著名定理之一,下面我们一起证明它的原命题:已知,如图,AD为△ABC的内角平分线求证:AD ²=AB·AC-BD·DC①辅助圆证法证明:延长AD交△ABC外交圆⊙O于点E连接BE由∠BAE=∠DAC, ∠E=∠C知△ABE∽△ADC∴AB = AE ∴AB·AC=AD·AEAD AC∵AE=AD+DE∴AB·AC=AD·AE=AD·(AD+DE)=AD²+AD·DE∵已知△BED∽△ACD∴AD =BD ∴AD·DE=DC·BDDC DE∴AB·AC=AD²+DC·BD即AD²=AB·AC-BD·DC②利用勾股定理证明过点A作AE⊥BC于点E,设点E在线段DC上设AD=t BD=m DC=n AC=b AB=c根据勾股定理:t²=AE²+DE²=b²-CE²+DE²=b²-(n-DE) ²+DE²=b²-n²+2Nde且t²=AE²+DE²=c²-BE²+DE²=c²-(m+DE) ²+DE ²=c²-m²-2m·DE∴DE= t²-b²+n²=c²-m²-t²2n 2m整理得:(m+n)t²=mb²+nc²-(m+n)mn根据内角平分线定理有: c = m ∴mb=ncb n而mb²=mb·b=nbc, nc²=nc·c=mbc∴(m+n)t²=(m+n)bc-(m+n)mn∴t²=bc-mn即AD²=AB·AC-BD·DCPS:其实,Schooten定理还可以用正弦定理以及和差化积推导出来,接下来我们一起尝试用正弦定理证明吧?③正弦定理证法证明:如图,设BD=m , DC=n, AD=t , AB=c,AC=b∠BAD=∠DAC=β, ∠ADC=α, ∠ADB=180°-α根据正弦定理:b =Sinα,c =Sin(180°-α)=Sinα, m =Sinβn =Sinβt SinC t SinB SinB t SinB t SinC∴b =Sinα·t , c =Sin(180°-α)=Sinα·t , m =Sinβ·t , n =Sinβ·t SinC SinB SinB SinB SinC∴bc-mn=Sinα·t·Sinα·t-Sinβ·t·Sinβ·tSinC SinB SinB SinC=Sin ²α-Sin ²β·t ²SinBSinC又∵Sin ²α-Sin ²β=(Sinα+Sinβ)(Sinα-Sinβ)=(2Sin(α+β)Cos(α-β)(2Cos(α+β)Sin(α-β) )2 2 2 2=Sin(α+β) ·Sin(α-β)由图,注意到α+β=180°-∠C, α-β=∠B∴Sin ²α-Sin ²β=Sin(180°-∠C) ·SinB=SinB·SinC∴bc-mn= SinB·SinC ·t ²=t ²SinB·SinC即AD ²=AB·AC-BD·DC补充说明:在①辅助圆证法中,我们得到了AD·DE=DC·BD这样的结论,这其实是一个普遍性的结论,也可以说是一个定理即“相交弦定理”如图,AB、CD是⊙O内的一对相交弦,交点为E则AE·BE=CE·DE另外,我们连接AC、BC、BD、AD,可得到一个圆内接四边形ABCD联系初中的几何知识, 我们知道∠CAD+∠CBD=180°, ∠ACB+∠ADB=180°反过来,在任意四边形中,只要存在一组对角互补,那么这个四边形就拥有一个外接圆,也就是存在一个圆使得这个四边形的四个顶点都在圆上,我们可称这个四个顶点共圆.如图,点A、C、B、D四点共圆(我们在二以及三的补充说明所作的努力,其实是为下面这个经典难题服务的)四.证明“三条角平分线对应相等的两个三角形全等”如图,设I是△A’B’C’的垂心,A、B、C是三条高的垂足,连接AB、BC、AC设AB与C’C交点于F,BC于AA’交于点E,AC与BB’交于点E设AD=Ta,BE=Tb,CF=Tc,ID=x,IE=y,IF=z易知点A、C’、B、I四点共圆,点A、B’、C、I四点共圆,点A’、B、I、C四点共圆∴∠ABI=∠AC’I , ∠IBC=∠IA’B’又∵∠AC’I=90°-∠C’B’C , ∠IA’B’=90°-∠C’B’C∴∠AC’I=∠IA’B’∴∠ABI=∠IBC ∴BE为△ABC的内角平分线同理可证AD、CF也为△ABC的角平分线∴点I为△ABC的内心∵BI是△ABD的内角平分线∴AB =AI =Ta-x =Ta -1 (内角平分线定理)BD ID x x∵BA’是△ABD的外角平分线∴AB =AA’ = AI+IA’= Ta-x+IA’= Ta +1 (外角平分线定理)BD DA’IA’-ID IA’-x IA’-X∴Ta +1= AB = Ta -1IA’-x BD x解这个方程(IA’为未知数)得IA’= 2x(Ta-x)²Ta-2x∴AI·A’I=(Ta-x) ·2x(Ta-x)= 2x(Ta-x) ²Ta-2x Ta-2x同理可证BI·IB’=2y(Tb-y)², CI·IC’= 2z(Tc-z)²Tb-2y Tc-2z∵A、B、A’、B’四点同圆∴AI·A’I=BI·B’I(相交弦定理)∵B、C、B’、C’四点共圆∴BI·IB’=CI·IC’∴2x(Ta-x)²= 2y(Tb-y)²= 2z(Tc-z)²Ta-2x Tb-2y Tc-2z∴设x =u , y =v , z =wTa Tb Tc代入上式得:Ta²·u(1-u)²=Tb²·v(1-v)²=Tc²·w(1-w)²(=k)1-2u 1-2v 1-2w单独对Ta²·u(1-u) ²=k分析1-2u设f(u)= u(1-2u)²= k1-2u Ta ²对f(u)的单调性进行判断,由于f(u )比较复杂,直接对其求导f’(u) = (1-u) (4u²-3u+1) = (1+u) [(2u-¾)²+7/16](1-2u)²(1-2u) ²∵u= x <1 ∴1-u>0 ∴f’(u) >0Ta可见f(u)是单调递增的函数,所以当Ta、k的值确定时,u的值是唯一确定的,而且当Ta的值确定时,u的值随k增大而增大同理,当Tb、k的值确定时,v的值是唯一确定的,而且当Tb的值确定时,v的值随k增大而增大当Tc、k的值确定时,w的值是唯一确定的,而且当Tc的值确定时,w的值随k增大而增大设BC=a ,AC=b, AB=c∵Ta -1= Ta-x = AB = AB+AC =AB+AC=c+bx x BD BD+DC BC a∴Ta = c+b +1= a+b+c 即有u= x = ax a a Ta a+b+c同理有v= y = b , w= z = cTb a+b+c Tc a+b+cu+v+w= a + b + c =1a+b+c a+b+c a+b+c由前面推导可知,当Ta、Tb、Tc的值确定时,u+v+w的值随k的增大而增大,现在又知道u+v+w=1,可见k的值不能任意改变,是唯一确定的但是又有u∶v∶w= a ∶ b ∶ c =a∶b∶ca+b+c a+b+c a+b+c可见当内角平分线的长度Ta、Tb、Tc确定时,△ABC三边的比值也是唯一确定的.这也就是,当两个三角形的内角平分线对应相等时,这两个三角形必定相似,不仅如此,如果这两个三角形的相似比不是1,它们的内角平分线不会对应相等,可见它们的相似比一定是1,所以这两个三角形一定相等.总结:从一到四,我们一共讨论了五个有关三角形角平分线的题,这些题目有些简单一看就懂;有的复杂,初看之后无从下手.我很喜欢张景中院士的一句话:“题目的难易取决于解题方法.”没错,有些“难题”一开始我们可能会无法解决,但只要我们在平常多积累有些巧妙的数学思想、解题方法,我们总有一天会解开,而且解题方法还可能简单的难以置信.一个个定理的相互联系也会让我们体会到数学的严密性、逻辑性.“数学是宇宙中最美得语言”我希望我能与大家一起热爱数学、探索数学,感受数学之美.注:参考文献《新概念几何》张景中P224《几何变换与几何证明》萧振刚P368、。

三角形角平分线的结论及应用浅议三角形角平分线的结论及应用摘要:一个角的平分线是一条射线,而三角形的角平分线是一条线段。
本文主要谈两点:关于三角形的内、外角平分线的夹角的问题和关于三角形内、外角平分线的交点问题。
关于三角形的内、外角平分线的夹角问题:(1)三角形两内角平分线的夹角等于90度与三角形第三个内角的一半的和。
(2)三角形两外角平分线的夹角等于90度与三角形第三个内角的一半的差。
(3)三角形一个内角的平分线与一个外角平分线的夹角等于三角形第三个内角的一半(4)三角形两内角平分线的夹角与两外角平分线的夹角互补或相等。
关于三角形内外角平分线的交点问题:(5)三角形的三条内角平分线相交于一点,这点到三角形的三边的距离相等(6)三角形两外角平分线的交点到三角形三边所在的直线相等,并且这点在三角形第三个内角的平分线上等关键词:三角形角平分线夹角交点变式练习一个三角形的角平分线不外乎就是内角的平分线和外角的角平分线。
在学习过程中,教师要指导学生善于对三角形的角平分线的基本图形进行归纳,对角平分线的性质和结论做好总结,这样对以后知识的积累有很大的帮助,对解决复杂的几何证明题也更便捷。
下面就三角形角平分线的相关结论逐一探讨。
结论一:如图1、在△ABC中,∠ABC、∠ACB的角平分线的交与点D,1∠A。
试探究:∠D=90°+2解:∵BD、CD为角平分线1∠ABC,(图1)∴∠CBD=21∠ACB。
∠BCD=2在△BCD中:∠D=180°-(∠CBD+∠BCD)1(∠ABC+∠ACB)=180°-21(180°-∠A)=180°-21∠A=90°+2变式练习的题目有(1)如图2、在△ABC中,∠ABC、∠ACB的角平分线的交与点D,∠D=100°,则∠A的度数是度。
1∠A。
则∠A=2∠D―180°,解:由结论1得知,∠D=90°+2容易得出∠A=20°(图2)(2)如图3: 在四边形ABCD中,∠D=120°,∠A=100°∠ABC、∠ACB的角平分线的交与点E,试求∠BEC的度数。
证明命题三角形的两条内角平分线所夹的锐角命题:在三角形ABC中,角BAD和角CAD所夹的夹角小于角BAC。
证明:1. 这个命题是一个基本的几何命题,我们需要进行推导和证明。
我们知道内角平分线是三角形内部角的平分线,也就是说,它将一个角分成两个等角。
我们可以设角BAD和角CAD的平分线分别交BC和AB 于点E和F。
我们需要证明角BEF小于角BAC。
2. 我们可以找到角BAD和角CAD的平分线的交点,设为点P。
那么我们可以得到两个三角形:三角形BAP和三角形CAP。
由于平分线的定义,我们知道角BAP等于角CAP。
3. 接下来,我们需要证明三角形BEP和三角形CFP是全等三角形。
我们知道BE和CF是角BAD和角CAD的平分线,所以它们分别等于BP和CP。
另外,根据共有边EP=FP,因此根据边角边全等定理,可以得出三角形BEP全等于三角形CFP。
4. 由于全等三角形的性质,我们知道对应角相等。
角BEF等于角CFP。
另外,我们知道三角形BEP和三角形CFP是全等三角形,所以角BEP 等于角CFP。
5. 综合以上推导,我们得到角BEF等于角BEP加上角EPF,而角BAC 等于角BAP加上角PAE。
另外,由于三角形BEP和三角形CFP是全等三角形,角BEP等于角CFP,而角BAP等于角CAP。
角BAC等于角PAE加上角CAF。
而根据平行线性质,我们知道角PAE等于角CAF。
6. 将以上推导综合起来,我们得到角BEF小于角BAC。
结论:通过以上推导和证明,我们证明了命题三角形的两条内角平分线所夹的锐角小于角BAC。
这个命题在几何学中具有重要意义,也是我们理解和掌握三角形内角平分线性质的基础。
在实际生活中,我们可以通过这个命题解决很多相关问题,比如构造垂直平分线、内切圆等。
掌握并理解这个命题对我们深入学习几何学和解决实际问题都具有重要意义。
个人观点:对于证明命题三角形的两条内角平分线所夹的锐角这一命题,我认为它是几何学中的一个基本命题,但是它的证明过程需要严密的逻辑推导和几何知识的灵活运用。
三角形内外角平分线一.命题的证明及应用在中考常有与三角形内外角平分线有关的题目,若平时不注意总结是很难一下子解决的.下面来一起学习一下.命题1 如图1,点D是△ABC两个内角平分线的交点,则∠D=90°+∠A.证明:如图1:∵∠1=∠,∠2=∠,∴2∠1+2∠2+∠A=180°①∠1+∠2+∠D=180°②①-②得:∠1+∠2+∠A=∠D③由②得:∠1+∠2=180°-∠D④把③代入④得:∴180°-∠D+∠A=∠D∠D=90°+∠A.点评利用角平分线的定义和三角形的内角和等于180°,不难证明.命题2 如图2,点D是△ABC两个内角平分线的交点,则∠D=90°-∠A.证明:如图2:∵DB和DC是△ABC的两条外角平分线,∴∠D=180°-∠1-∠2=180°-(∠DBE+∠DCF)=180°-(∠A+∠4+∠A+∠3)=180°-(∠A+180°)=180°-∠A-90°=90°-∠A;点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和以及三角形的内角和等于180°,可以证明.命题3 如图3,点E是△ABC一个内角平分线与一个外角平分线的交点,则∠E=∠A.证明:如图3:∵∠1=∠2,∠3=∠4,∠A+2∠1=2∠4①∠1+∠E=∠4②①×代入②得:∠E=∠A.点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和,很容易证明.命题4如图4,点E是△ABC一个内角平分线BE与一个外角平分线CE的交点,证明:AE是△ABC的外角平分线.证明:如图3:∵BE是∠ABC的平分线,可得:EH=EFCE是∠ACD的平分线, 可得:EG=EF∴过点E分别向AB、AC、BC所在的直线引垂线,所得的垂线段相等.即EF=EG=EH∵EG=EH∴AE是△ABC的外角平分线.点评利用角平分线的性质和判定能够证明.应用上面的结论能轻松地解答一些相关的比较复杂的问题,下面来一起看.例1如图5,PB和PC是△ABC的两条外角平分线.①已知∠A=60°,请直接写出∠P的度数.②三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形?解析:①由命题2的结论直接得:∠P=90°-∠A=90°-×60°=60°②根据命题2的结论∠P=90°-∠A,知三角形的三条外角平分线所在的直线形成的三角形的三个角都是锐角,则该三角形是锐角三角形.点评此题直接运用命题2的结论很简单.同时要知道三角形按角分为锐角三角形、直角三角形和钝角三角形.例2如图6,在△ABC中,延长BC到D,∠ABC与∠ACD的角平分线相较于点,∠BC与∠CD的平分线交与点,以此类推,…,若∠A=96°,则∠= 度.解析:由命题③的结论不难发现规律∠∠A.可以直接得:∠=×96°=3°.点评此题是要找出规律的但对要有命题③的结论作为基础知识.例3(203陕西第一大题填空题第八小题,此题3分)如图7,△ABC的外角∠ACD 的平分线CP的内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP=_______________.解析:此题直接运用命题4的结论可以知道AP是△ABC的一个外角平分线,结合命题3的结论知道∠BAC=2∠BPC, CAP=(180°-∠BAC )= (180°-2∠BPC )=50°.点评对命题3、4研究过的读者此题不难,否则将是一道在考试的时候花时间也不一定做的出来的题目.例4(2003年山东省)如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角平分线交与E点,连接AE,则∠AEB= 度.解析:有题目和命题4的结论可以知道AE是△ABC的一个外角平分线, 结合命题2的结论知道∠AEB=∠ACB-∠ACB=90°-×90°=45°点评从上面的做题过程来看题目中给出的“∠A=30°”这个条件是可以不用的.二.角平分线定理使用中的几种辅助线作法一、已知角平分线,构造三角形例题、如图所示,在△ABC 中,∠ABC=3∠C ,AD 是∠BAC 的平分线,BE ⊥AD 于F 。
三角形内角与外交平分线定理一、内角平分线定理:如下图,AD 是△ABC 的内角∠BAC 的平分线。
求证: BA/AC=BD/DC;思路1:过C 作角平分线AD 的平行线。
证明1:过C 作CE ∥DA 与BA 的延长线交于E 。
那么: BA/AE=BD/DC;∵ ∠BAD=∠AEC ;〔两线平行,同位角相等〕∠CAD=∠ACE ;〔两线平行,内错角相等〕∠BAD=∠CAD ;〔〕∴ ∠AEC=∠ACE ;〔等量代换〕∴ AE=AC ;∴ BA/AC=BD/DC 。
结论1:该证法具有普遍的意义。
引出三角形内角平分线定理:三角形任意两边之比等于它们夹角的平分线分对边之比。
思路2:利用面积法来证明。
:如图8-4乙所示,AD 是△ABC 的内角∠BAC 的平分线。
求证: BA/AC=BD/DC证明2:过D 作DE ⊥AB 于E ,DF ⊥AC 于F ;∵ ∠BAD=∠CAD ;〔〕∴ DE=DF ;∵ BA/AC=S △BAD/S △DAC ; 〔等高时,三角形面积之比等于底之比〕BD/DC=S △BAD/S △ABCDAC ;〔同高时,三角形面积之比等于底之比〕∴ BA/AC=BD/DC结论2:遇到角平分线,首先要想到往角的两边作平行线,构造等腰三角形或菱形,其次要想到往角的两边作垂线,构造翻转的直角三角形全等,第三,要想到长截短补法。
二、外角平分线定理:如下图,AD 是△ABC 中∠BAC 的外角∠CAF 的平分线。
求证: BA/AC=BD/DC思路1:作角平分线AD 的平行线。
证明1:过C 作CE ∥DA 与BA 交于E 。
那么: BA/AE=BD/DC∵ ∠DAF=∠CEA ;〔两线平行,同位角相等〕∠DAC=∠ECA ;〔两线平行,内错角相等〕∠DAF=∠DAC ;〔〕∴ ∠CEA=∠ECA ;〔等量代换〕∴ AE=AC ;∴ BA/AC=BD/DC 。
ABC AD BAC AB BD AC CD ∠=在中,若为的平分线,则:结论1:该证法具有普遍的意义。
三角形内外角平分线的结论及应用
三角形内外角平分线是一个重要的数学概念,它在一定程度上能够影响多个分支的结果。
在互联网等新兴领域,三角形内外角平分线也被广泛应用,将成为其未来发展的参照系。
从数学角度来讲,三角形内外角平分线可以定义为在一个三角形中,从一条边中分别垂直于另外两条边的两个对角线。
据定理,内角平分线能够将内角分割为两个相等的小角,而外角平分线能够将外角分割为两个非常接近的小角,其精确性可达到数量级。
随着互联网的发展,三角形内外角平分线被广泛应用于各种领域。
一是应用于一些基础性的技术领域,如导航系统,这种导航系统需要根据三角形内外角平分线的定义和技术,将目的地的所在的平面区域分成完整的几何图形;二是应用于金融行业,利用金融市场的动态性,以及投资者对三角形内外角平分线的了解,投资者可以合理地进行风险投资,并获取较高回报。
总之,三角形内外角平分线是一个具有重要意义的数学概念,它的应用可以广泛地应用于各种互联网领域,未来可以有更大的作用。
三角形内外角平分线有关命题的证明及应用
在中考和一些竞赛题目中常有与三角形内外角平分线有关的题目,若平时不注意总结是很难一下子解决的.下面来一起学习一下.命题 1 如图1,点D是△ABC两个内角平分线的交点,则∠D=90°+∠A.
证明:如图1:
∵∠1=∠,∠2=∠,
∴2∠1+2∠2+∠A=180°①
∠1+∠2+∠D=180°②
①-②得:
∠1+∠2+∠A=∠D③
由②得:
∠1+∠2=180°-∠D④
把③代入④得:
∴180°-∠D+∠A=∠D
∠D=90°+∠A.
点评利用角平分线的定义和三角形的内角和等于180°,不难证明.
命题 2 如图2,点D是△ABC两个内角平分线的交点,则∠D=90°-∠A.
证明:如图2:
∵DB和DC是△ABC的两条外角平分线,
∴∠D=180°-∠1-∠2
=180°-(∠DBE+∠DCF)
=180°-(∠A+∠4+∠A+∠3)
=180°-(∠A+180°)
=180°-∠A-90°
=90°-∠A;
点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和以及三角形的内角和等于180°,可以证明.
命题3 如图3,点E是△ABC一个内角平分线与一个外角平分线的交点,则∠E=∠A.
证明:如图3:
∵∠1=∠2,∠3=∠4,
∠A+2∠1=2∠4①
∠1+∠E=∠4②
①×代入②得:
∠E=∠A.
点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和,很容易证明.
命题4如图4,点E是△ABC一个内角平分线BE与一个外角平分线CE的交点,证明:AE是△ABC的外角平分线.
证明:如图3:
∵BE是∠ABC的平分线,可得:EH=EF
CE是∠ACD的平分线, 可得:EG=EF
∴过点E分别向AB、AC、BC所在的直线引垂线,所得的垂线段相等.
即EF=EG=EH
∵EG=EH
∴AE是△ABC的外角平分线.
点评利用角平分线的性质和判定能够证明.
应用上面的结论能轻松地解答一些相关的比较复杂的问题,下面来一起看.
例1如图5,PB和PC是△ABC的两条外角平分线.
①已知∠A=60°,请直接写出∠P的度数.
②三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形?
解析:①由命题2的结论直接得:∠P=90°-∠A=90°-×60°=60°
②根据命题2的结论∠P=90°-∠A,知三角形的三条外角平分线所在的直线形成的三角形的三个角都是锐角,则该三角形是锐角三角形.
点评此题直接运用命题2的结论很简单.同时要知道三角形按角分为锐角三角形、直角三角形和钝角三角形.
例2如图6,在△ABC中,延长BC到D,∠ABC与∠ACD的角平分线相较于点,∠BC与∠CD的平分线交与点,以此类推,…,若∠A=96°,则∠= 度.
解析:由命题③的结论不难发现规律∠∠A.
可以直接得:∠=×96°=3°.
点评此题是要找出规律的但对要有命题③的结论作为基础知识.
例3(2011湖北鄂州市中考第一大题填空题第八小题,此题3分)如图7,△ABC的外角∠ACD的平分线CP的内角∠ABC平分线BP 交于点P,若∠BPC=40°,则∠CAP=_______________.
解析:此题直接运用命题4的结论可以知道AP是△ABC的一个外角平分线,结合命题3的结论知道∠BAC=2∠BPC, CAP=(180°-∠BAC )= (180°-2∠BPC )=50°.
点评对命题3、4研究过的读者此题不难,否则将是一道在考试的时候花时间也不一定做的出来的题目.
例4(2003年山东省“KLT快乐灵通杯”初中数学竞赛试题)如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角平分线交与E点,连接AE,则∠AEB= 度.
解析:有题目和命题4的结论可以知道AE是△ABC的一个外角平分线, 结合命题2的结论知道∠AEB=∠ACB-∠ACB=90°-×90°=45°
点评从上面的做题过程来看题目中给出的“∠A=30°”这个条件是可以不用的.。