第3章 正弦稳态电路分析习题讨论课
- 格式:doc
- 大小:952.00 KB
- 文档页数:4




电工技术第3章(李中发版)课后习题及详细解答(总41页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第3章单相正弦电路分析已知正弦电压(V)、(V),则u1与u2的相位差为,是否正确为什么分析讨论相位差问题时应当注意,只有同频率正弦量才能对相位进行比较。
这是因为只有同频率正弦量在任意时刻的相位差是恒定的,能够确定超前、滞后的关系,而不同频率正弦量的相位差是随时间变化的,无法确定超前、滞后的关系,因此不能进行相位的比较。
解不正确。
因为u1的角频率为ω,而u2的角频率为2ω,两者的频率不同,相位差随时间变化,无法确定超前、滞后的关系,因此不能进行相位的比较。
已知某正弦电流的有效值为10 A,频率为50 Hz,初相为45°。
(1)写出该电流的正弦函数表达式,并画出波形图;(2)求该正弦电流在s时的相位和瞬时值。
解(1)由题设已知正弦电流的有效值A,频率Hz,初相。
由频率f可得角频率ω为:(rad/s)所以,该电流的正弦函数表达式为:(A)波形图如图所示。
(2)s时的相位为:(rad)瞬时值为:(A)已知正弦电流(A)、(A),试求i1与i2的振幅、频率、初相、有效值和相位差,并画出其波形图。
2解i1与i2的振幅分别为:(A)(A)频率分别为:(Hz)初相分别为:有效值分别为:(A)(A)i1与i2的相位差为:说明i1超前i2。
波形图如图所示。
图习题解答用图图习题解答用图设,,试计算、、AB 、。
分析复数可用复平面上的有向线段、代数型、三角函数型和指数型(极坐标型)等形式表示。
复数的加减运算就是将实部和虚部分别进行加减,因而采用代数型比较方便。
复数的乘法运算就是将模相乘而辐角相加,复数的除法运算就是将模相除而辐角相减,因而采用指数型(极坐标型)比较方便。
解34写出下列各正弦量所对应的相量,并画出其相量图。
(1)(mA ) (2)(A )(3)(V ) (4)(V )分析 用相量来表示正弦量,就是用一个复数来反映正弦量的振幅(或有效值)和初相,即用相量的模来代表正弦量的振幅(或有效值),用相量的辐角来代表正弦量的初相。
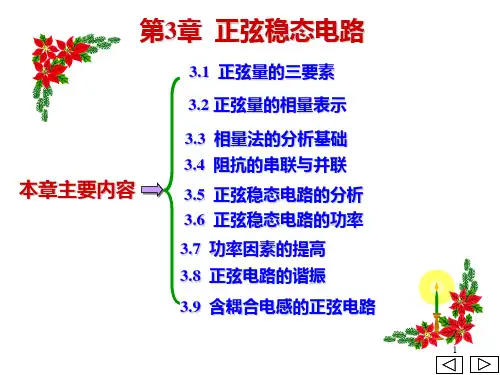



第3章 正弦稳态电路分析习题讨论课Ⅰ 本章要奌归纳1、正弦量的三要素:),(,T f U m ω,ϕ{要求:①由正弦时间函数、由波形会求三个“要素”;②由三个“要素”会写正弦时间函数、会画波形图。
}有效值:m U U 21=,m I I 21=;{注意:①交流电流表的读数一般为有效值;②若知有效值写时间函数表达式,一定将有效值换算为振幅值。
}相 量:{要求:①由正弦量u ,i 会写对应的相量I U,;②由相量再告知(ω或T 或f )会写相应的正弦时间函数。
}2、基本元件VCR 的相量形式R I R U= L I L j Uω=C Cj Uω1-= IKL 相量形式KCL 相量形式 ∑=0IKVL 相量形式∑=0U3、阻抗与导纳定义及其串并联等效⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+==jXR e Z I U Z zj ϕ (1) ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+==jB G e Y U I Y yj ϕ (2) 显然二者互为倒数关系:,1Y Z = ZY1=阻抗串、并联求等效阻抗的公式,串联分压、并联分流公式类同电阻串、并联相应的公式。
导纳串、并联求等效导纳的公式,串联分压、并联分流公式类同电导串、并联相应的公式。
C j ω1-注意这里的运算都是复数运算。
4.相量用于正弦稳态电路分析(1)正弦函数激励的线性时不变渐近稳定电路,且电路达到稳态,只求稳态响应,称正弦 稳态电路分析。
(2)若单一频率正弦函数激励源的正弦稳态电路分析,应用相量分析法。
基本思路:5、正弦稳态电路中的功率 (1)平均功率)cos(i u UI P ϕϕ-= (1)应用式(1)计算平均功率时,N 内含有电源不含电源均可使用。
若N 内不含电源,则z i u θϕϕ=- 则 z UI P θcos = (2)式(2)中z θcos 称功率因数,这时P 又称为有功功率。
(2)无功功率 z UI Q θsin =(3)视在功率 UI S =(4)复功率 S ~=jQ P +I U=*注意:整体电路与各部分电路间的几种功率关 k mk P P ∑==1∑==mk k Q Q 1∑==m k k S S 1~~ (S ≠)1∑=mk k S若为简单电路若为复杂电路::利用阻抗、导纳串并联等效,结合KCL 、KVL 求解。
第3章正弦电路稳态分析3.2.5 正弦电流电路的谐振(1)串联谐振的产生:谐振是由R、L、C元件组成的电路在一定条件下发生的一种特殊现象。
首先,我们来分析R、L、C串联电路发生谐振的条件和谐振时电路的特性。
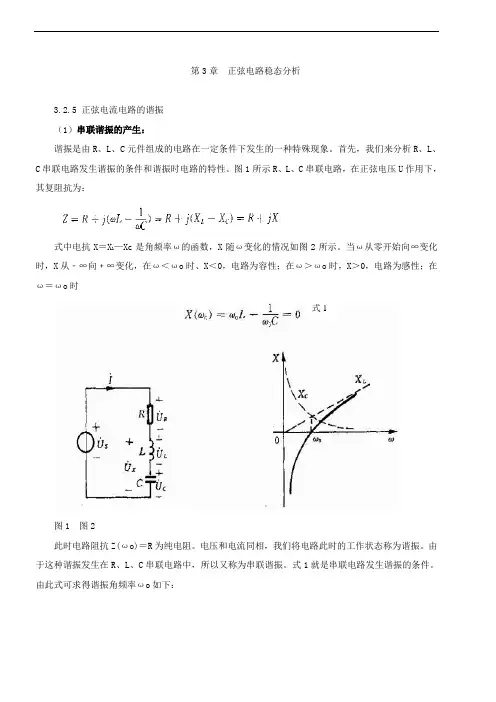
图1所示R、L、C串联电路,在正弦电压U作用下,其复阻抗为:式中电抗X=X l—Xc是角频率ω的函数,X随ω变化的情况如图2所示。
当ω从零开始向∞变化时,X从﹣∞向﹢∞变化,在ω<ωo时、X<0,电路为容性;在ω>ωo时,X>0,电路为感性;在ω=ωo时式1图1 图2此时电路阻抗Z(ωo)=R为纯电阻。
电压和电流同相,我们将电路此时的工作状态称为谐振。
由于这种谐振发生在R、L、C串联电路中,所以又称为串联谐振。
式1就是串联电路发生谐振的条件。
由此式可求得谐振角频率ωo如下:谐振频率为由此可知,串联电路的谐振频率是由电路自身参数L、C决定的.与外部条件无关,故又称电路的固有频率。
当电源频率一定时,可以调节电路参数L或C,使电路固有频率与电源频率一致而发生谐振;在电路参数一定时,可以改变电源频率使之与电路固有频率一致而发生谐振。
串联谐振的品质因数:串联电路谐振时,其电抗X(ωo)=0,所以电路的复阻抗呈现为一个纯电阻,而且阻抗为最小值。
谐振时,虽然电抗X=X L—Xc=0,但感抗与容抗均不为零,只是二者相等。
我们称谐振时的感抗或容抗为串联谐振电路的特性阻抗,记为ρ,即ρ的单位为欧姆,它是一个由电路参数L、C决定的量,与频率无关。
工程上常用特性阻抗与电阻的比值来表征谐振电路的性能,并称此比值为串联电路的品质因数,用Q表示,即品质因数又称共振系数,有时简称为Q值。
它是由电路参数R、L、C共同决定的一个无量纲的量。
谐振时各元件的电压分别为即谐振时电感电压和电容电压有效值相等,均为外施电压的Q 倍,但电感电压超前外施电压900,电容电压落后外施电压900,总的电抗电压为0。
而电阻电压和外施电压相等且同相,外施电压全部加在电阻R 上,电阻上的电压达到了最大值。

第三章 正弦交流稳态电路的分析第一节 学习指导一、学习目的和要求1.理解正弦量的三要素,特别是有效值和相位差。
2.熟悉正弦量的各种表示方法以及相互间的关系。
3.掌握单一参数的电压、电流之间的关系,并掌握用相量法计算简单的交流电路的方法。
4.掌握有功功率和功率因数的计算,了解瞬时功率、无功功率、视在功率的概念和提高功率因数方法和意义。
5.掌握串联谐振的特点,谐振频率、品质因数的计算,了解并联谐振。
6.掌握三相电路中相电压(相电流)与线电压(线电流)在对称三相电路中的相互关系。
7.理解三相四线制电路中单相及三相负载的正确联接,了解中性线的作用。
8.掌握对称三相电路的电压,电流和功率。
9.了解交流电路的频率特性。
二、内容简介1.正弦交流电参考方向交流电压的极性和电流的方向是随时间而交变的,它们的参考方向是指其在正半周时的实际方向。
2.正弦量的三要素(频率、幅值和初相位)。
(1)频率f 、周期Τ和角频率ω:表示正弦量变化的快慢,三者关系为T f ππω22==(2)有效值和幅值:表示正弦量的大小。
幅值或最大值:用m U ,m E ,m I 表示。
有效值是根据交流电流和直流电流具有相等的热效应来定义的。
mI dt i T I 2112==⎰,2m U U =,2m E E =。
上述关系只适用于任何周期性变化量,不能用于非周期量。
瞬时值:用e i u ,,表示。
(3)初相位是表示正弦量初始值的。
()ψω+t 为正弦量的相位,它反映正弦量的变化进程。
0=t 时的相位ψ为初相位。
相位差:两个同频率的正弦量相位之差即初相位之差。
它不随计时起点而变。
(见表3-1所示)表3-1 初相位与相位差3.正弦量的表示方法(见表3-2所示)表3-2 正弦量的表示方法,sin(m I I I ≠4.单一元件交流电路特性本章所讲的电路元件是指理想元件。
电阻元件是耗能元件,电感元件和电容元件是储能元件。
重要特性:电感中电流不能跃变,电容中电压不能跃变。
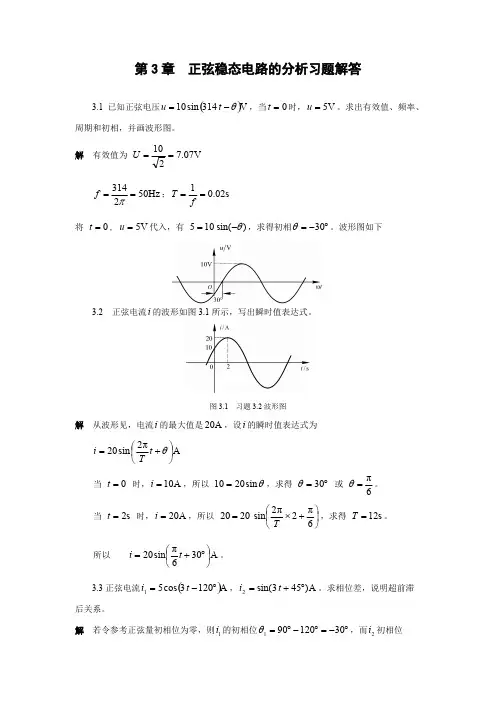
第3章 正弦稳态电路的分析习题解答3.1 已知正弦电压,当时,。
求出有效值、频率、()V 314sin 10θ-=t u 0=t V 5=u 周期和初相,并画波形图。
解 有效值为 V07.7210==U ;Hz 502314==πf s 02.01==f T 将 , 代入,有 ,求得初相。
波形图如下0=t V 5=u )sin(105θ-=︒-=30θ3.2 正弦电流的波形如图3.1所示,写出瞬时值表达式。
i图3.1 习题3.2波形图解 从波形见,电流的最大值是,设的瞬时值表达式为i A 20i A π2sin 20⎪⎭⎫ ⎝⎛+=θt T i 当 时,,所以 ,求得或 。
0=t A =10i θsin 2010=︒=30θ6π=θ当 时,,所以 ,求得 。
s 2=t A =20i ⎪⎭⎫ ⎝⎛+⨯=6π2π2sin 2020Ts 12=T 所以 。
A ⎪⎭⎫ ⎝⎛︒+=306πsin 20t i 3.3正弦电流,。
求相位差,说明超前滞()A 120 3cos 51︒-=t i A )45 3sin(2︒+=t i 后关系。
解 若令参考正弦量初相位为零,则的初相位,而初相位1i ︒-=︒-︒=30120901θ2i,其相位差 , 所以滞后于 角,或︒=452θ︒-=︒-︒-=-=75453021θθϕ1i 2i ︒75超前 角。
2i 1i ︒753.4 正弦电流和电压分别为(1)V)60 4sin(23o 1+=t u (2)V)75 4cos(52︒-=t u (3)A)90 4sin(2o 1+-=t i (4) V)45 4cos(252︒+-=t i 写出有效值相量,画出相量图。
解 (1) ,相量图如图(1)V 6031︒∠=∙U (2) V)15 4sin(5)75 4cos(52︒+=︒-=t t u 有效值相量为 ,相量图如图(2)V 15252︒∠=∙U (3) ()()A90 4sin 290 4sin 21︒-=︒+-=t t i 有效值相量为 ,相量图如图(3)A 9021︒-∠=∙I (4) ()()A45 4sin 2545 4cos 252︒-=︒+-=t t i 有效值相量为 ,相量图如图(4)A 4552︒-∠=∙I3.5 图3.2中,已知,,求。
3.2 正弦电流电路的分析 3.2.1 阻抗和导纳对一单口网络,端口电压相量与电流相量之比,定义为该网络的阻抗Z 。
单位(Ω)上式定义为欧姆定律的相量形式。
无源单口网络)的电路模型。
对于阻抗需要说明以下几点:(1)单一元件R 、L 、C 的阻抗分离为:(2)阻抗Z 取决于网络结构、元件参数和电源的频率。
(3)阻抗Z 是一个复数。
(直角坐标形式) 式中,实部R :电阻分量 虚部X :电抗分量(可正可负)倘若单口无源网络,端口上电压相量和电流相量参考方向一致,其导纳定义为其中导纳Y 的单位是西[门子](S ) 对导纳说明以下几点:(1)单一元件R 、L 、C 的导纳分离为: ••=IU Z •U •URZ R =LL X L Z j j ==ωC C X cZ j 1j-=-=ωϕψψ∠=-∠==Z IU I UZ i u IUZ =iu ψψϕ-=XR Z Z j +=∠=ϕRXarctan=ϕ22X R Z +=ϕcos Z R =ϕsin Z X =ϕZXR阻抗三角•U••=UI Y 11CC jB c j Y ===ω1(2)单口网络的Y 由网络结构、元件参数和电源的频率决定。
(3)导纳Y 是一个复数称为导纳角,它是电流和电压的相位差。
(直角坐标形式)式中:实部G :电导分量( 正当) 虚部B :电纳分量(可正可负)由单口无源网络的阻抗Z 和导纳Y 的定义可知,对于同一单口无源网络Z 与Y 互为倒数,即或注重:普通3.2.2 阻抗(导纳)的串联、并联和相量图 单口无源网络中各阻抗为串联时,等效阻抗为:n 个阻抗串联:普通单口无源网络中各阻抗为并联时,等效阻抗为:n 个电阻并联:G RY R ==1)u i U I U IY Y ϕϕϕ-∠=='=∴( UIY =ui ϕϕϕ-='ϕ'jBG Y +=YZ 1=ZY 1=RG 1≠XB 1≠∑==nk kZZ1∑==nk kY Y 13.2.3 正弦电流电路的功率 一.瞬时功率如图所示的随意一端口电路N 0,在端口的电压u 与电流i 的参考方向对电路内部关联下,其吸收瞬时功率()()()p t u t i t =⋅若设正弦稳态一端口电路的正弦电压和电流分离为()cos u t t ω=()cos()i t t ωϕ=-式中u 0ψ=为正弦电压的初相位,i ψϕ=-为正弦电流的初相位,Z u i ψψψϕ=-=为端口上电压与电流的相位差。
第3章 正弦稳态电路分析习题讨论课
Ⅰ 本章要奌归纳
1、正弦量的三要素:),(,T f U m ω,ϕ{要求:①由正弦时间函数、由波形会求三个“要
素”;②由三个“要素”会写正弦时间函数、会画波形图。
}
有效值:m U U 21=
,m I I 2
1
=;{注意:①交流电流表的读数一般为有效值;②若知有效值写时间函数表达式,一定将有效值换算为振幅值。
}
相 量:{要求:①由正弦量u ,i 会写对应的相量I U
,;②由相量再告知(ω或T 或f )会写相应的正弦时间函数。
}
2、基本元件VCR 的相量形式
R I R U
= L I L j U
ω=
C C
j U
ω1-= I
KL 相量形式
KCL 相量形式 ∑=0I
KVL 相量形式
∑=0U
3、阻抗与导纳定义及其串并联等效
⎪⎭
⎪
⎬⎫⎪⎩⎪⎨⎧+==
jX
R e Z I U Z z
j ϕ (1) ⎪⎭
⎪⎬⎫⎪⎩⎪⎨⎧+==jB G e Y U I Y y
j ϕ (2) 显然二者互为倒数关系:,1Y Z = Z
Y
1
=
阻抗串、并联求等效阻抗的公式,串联分压、并联分流公式类同电阻串、并联相应的公式。
导纳串、并联求等效导纳的公式,串联分压、并联分流公式类同电导串、并联相应的公式。
C j ω1-
注意这里的运算都是复数运算。
4.相量用于正弦稳态电路分析
(1)正弦函数激励的线性时不变渐近稳定电路,且电路达到稳态,只求稳态响应,称正弦 稳态电路分析。
(2)若单一频率正弦函数激励源的正弦稳态电路分析,应用相量分析法。
基本思路:
5、正弦稳态电路中的功率 (1)平均功率
)cos(i u UI P ϕϕ-= (1)
应用式(1)计算平均功率时,N 内含有电源不含电源均可使用。
若N 内不含电源,则z i u θϕϕ=- 则 z UI P θcos = (2)
式(2)中z θcos 称功率因数,这时P 又称为有功功率。
(2)无功功率 z UI Q θsin =
(3)视在功率 UI S =
(4)复功率 S ~
=jQ P +I U
=* 注意:整体电路与各部分电路间的几种功率关 k m
k P P ∑
==
1
∑==m
k k Q Q 1
∑==m k k S S 1
~
~ (S ≠)1
∑=m
k k S
若为简单电路若为复
杂电路::
利用阻抗、导纳串并联等
效,结合KCL 、KVL 求解。
应用网孔法、节奌法、等
效电源定理求解。
Ⅱ基本概念问题讨论
1.是非问题判断(下列各命题,若判断是正确的请在题后括号内打“√”号;若判断是错误的请打“×”号。
)
(A )正弦函数激励的线性时不变渐近稳定的电路,电路达稳态时电感相当于短路,电容相当于开路。
( ) (B )正弦稳态电路中的电感上u 、i 参考方向如图中所标,则电感上电压超前电流90 。
( )
2.改错题 {下列各小题的答案均是错误的,请将改正为正确答案}
(A) 图示正弦稳态电路,已知t=t 1时 A t i A t i A t i 6)(,10)(,3)(131211-=== 则
A t i 5)(1=
(B) 图示正弦稳态电路,已知=)(1t i A t t i A t )60cos(24)(,)60sin(232
+=+ωω,
则电流表读数为7A 。
(C) 图示正弦稳态电路,已知100=s
U ∠0 V ,则
Ⅲ 综合举例
1、 如图所示正弦稳态电路,已知 V U U U C R L 10===(有效值),求电源
电压有效值s U 。
)(
3t 2
读数为1A 读数为0A 读数为0A
读数为0V
解:设 R
R U U = ∠0 V 则电流 110
10==
=R U I R R ∠0 A
电压 10=L
U ∠90 V , 10=C U ∠-90
V 所以 ,10Ω==j I U Z R L
L Ω-==10j I U Z R
C C
阻抗 Ω=++=10C L ab Z R Z Z , 10(=cd Z ∥ab Z )= 5Ω
电压 s
cd
cd U Z Z U
+=10=10=R ab I Z ∠0 即
105
105=+s U , 故得 30=s U ∠0 V 所以电源电压有效值 V U s 30=
2. 如图所示正弦稳态电路,且知I U
,同相位,U =20V ,电路吸收的平均功率P =100W ,求L C X X ,。
解:由 UI UI P z ==θcos =100 ∴ A I 520
100
==
阻抗 Ω==4I
U
Z ab (1) 由电路图写阻抗
)2525(2555)(5222
C
C
L
C C C C L ab X X X j X X jX jX jX Z +-++=--⨯+= (2) 令(2)式=(1)式,有
425522=+C
C
X X → 解得 Ω=10C X (负根舍去,无意义) 025252=+-C
C
L X X X → 解得 Ω=2L X
jX Ω
5j ωL
C
j
ω-R
U。