电路第九章(第26讲)(20091203) 正弦稳态电路分析习题课)
- 格式:ppt
- 大小:1.54 MB
- 文档页数:51
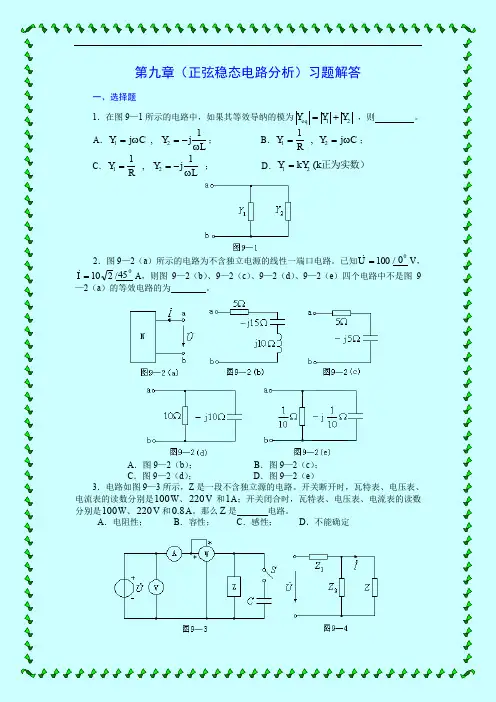
第九章(正弦稳态电路分析)习题解答一、选择题1.在图9—1所示的电路中,如果其等效导纳的模为21Y Y Y eq += ,则 。
A .L Y C Y ω-=ω=1j, j 21; B .C Y RY ω==j , 121;C .L Y R Y ω-==1j , 121 ;D .正为实数)k kY Y ( 21=2.图9—2(a )所示的电路为不含独立电源的线性一端口电路。
已知00 /100=UV ,045 /210=I A ,则图9—2(b )、9—2(c )、9—2(d )、9—2(e )四个电路中不是图9—2(a )的等效电路的为 。
A .图9—2(b );B .图9—2(c );C .图9—2(d );D .图9—2(e )3.电路如图9—3所示,Z 是一段不含独立源的电路。
开关断开时,瓦特表、电压表、电流表的读数分别是100W 、220V 和1A ;开关闭合时,瓦特表、电压表、电流表的读数分别是100W 、220V 和8.0A 。
那么Z 是 电路。
A .电阻性;B .容性;C .感性;D .不能确定4.电路如图9—4所示,U固定不变。
如果 ,则改变Z (Z 不等于无限大)时,I不变。
A .21Z Z =; B .21Z Z -=; C .21Z Z =; D .)Arg()Arg(21Z Z =5.Ω=10R 的电阻,F 1μ=C 的电容与电感L 串联,接到频率1000Hz 的正弦电压源上。
为使电阻两端的电压达到最高,电感应取 。
A .1H ;B .π21H; C .21H ; D .241πH二、填空题1.若Ω=3R ,Ω=ω6L ,Ω=ω2011C ,Ω=ω2012C ,则图9—5所示电路的输入阻抗为 j4)3(-Ω。
.2.线性一端口电路如图9—6所示,A /02 V ,30/5000=-=I U。
则此一端口电路吸收的复功率,有功功率、无功功率分别为V A 30/1000、W 350、50Var 。

第九章 正弦稳态电路的分析计算下列各题,并说明电路的性质。
(1)??,55,30100==Ω+=∠=••P I j Z V U(2)???,1653,153000===-∠-=∠=••P X R A I V U(3)???,5,301000300====∠-=-••P X R A e I V U j在如图所示的各电路图中,除A 0和V 0外,其余电流表和电压表的读数在图上都已标出(都是正弦量的有效值),试求电流表A 0或电压表V 0的读数。
在RLC 串联电路中,已知,Ω=50R ,mH L 60=,F C μ100=s rad /1000=ω,V U C ︒∠=010&,试求:(1)电路的阻抗Z ;(2)电流•I 和电压•U 、•L U 及有功功率P 、Q 、S ;(3)绘电压、电流相量图。
在图示电路中,V )30314sin(23600+=t u ,R 1=32,R 2=60,X 1=48,X 2=80。
求总电流i ,总有功功率P 及总功率因数。
I.I .I .U .R R j j 1212XX 12+-在如图所示的电路中,,51A I =,252A I =,110V U =,5Ω=R ,2L X R =试求,I ,C X L X 2R 及。
在如图所示的电路中,i u V U A I I 与,100,1021===同相,试求L C X X R I 及,,。
单相交流电路如图所示,已知ο&60401∠=U V ,Ω=5C X ,Ω==4L X R 。
求:(1)电流I &及电压2U &、U &;(2)电路的P 、Q 、S 。
图示电路中,并联负载Z 1、Z 2的电流分别为I 1=10 A ,I 2=20 A ,其功率因数分别为)0(6.0cos ),0(8.0cos 222111>==<==ϕϕλϕϕλ,端电压U =100 V ,ω=1000 rad/s 。



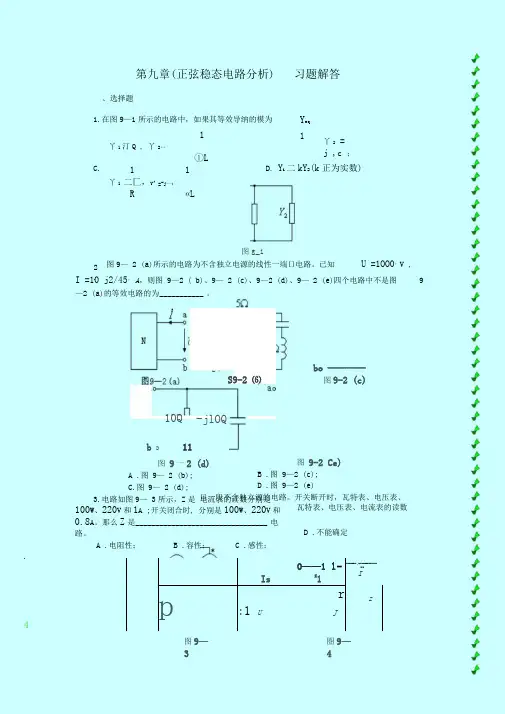
、选择题第九章(正弦稳态电路分析)习题解答1.在图9—1所示的电路中,如果其等效导纳的模为C .1丫1汀Q , 丫2…①L11 丫1 二匚,Y^ =-j —;R«LY eq1丫2 =j ,c ;D . Y i 二kY 2(k 正为实数)图g_i图9— 2 (a )所示的电路为不含独立电源的线性一端口电路。
已知U =1OO0°V ,I =10 j2/45° A ,则图 9—2 ( b )、9— 2 (c )、9—2 (d )、9— 2 (e )四个电路中不是图 9—2 (a )的等效电路的为 ___________ 。
2. S9-2 ⑹10Q -jlOQbo --------图9-2 (c)b D11图 9一2 (d)A .图 9— 2 (b );C .图 9— 2 (d );3.电路如图9— 3所示,Z 是 电流表的读数分别是100W 、220V 和1A ;开关闭合时, 分别是100W 、220V 和0.8A 。
那么Z 是 _________________________________ 电路。
A .电阻性;B .容性;C .感性;图 9-2 Ce)B .图 9—2 (c ); D .图 9—2 (e ) 旦一段不含独立源的电路。
开关断开时,瓦特表、电压表、 瓦特表、电压表、电流表的读数 D .不能确定%O ——1 l -IsZ1---------- ► -----------------■■I 4pr:1 UJTz图9—圏9—入阻抗为(3 - j4)门。
09-52 .线性一端口电路如图 9—6所示, 吸收的复功率,有功功率、无功功率分别为U - -50 /300V, I =2/0^A 。
则此一端口电路100/30°VA 、50 .. 3W 、50Var 。
4.在图9 — 8所示电路中,已知电流表 表V 2的读数为20 V ,则电压表V 的读数为A 的读数为2A ,电压表V 的读数10V ,电压V 。



第九章正弦交流稳态电路习题9—1 图9—25所示电路,当开关S 合上和断开时,电流表的读数不变,求:L X 和C X 的关系。
9—2 图9—26所示电路正弦交流电路,电压60=U V ,Ω=Ω=40,40C X R ,开 关S 于位置1时,电压表的读数○V =48V 。
求:开关S 于位置2时电压表的读数。
图9—25 图9—269—3图9—27所示电路,222L R U U U +=是否正确?试用相量图说明。
9—4 图9—28所示电路正弦交流电路中,已知Ω=10R ,Ω=101C ,bc ab U U =,U与I同相。
求:电路的阻抗Z 。
图9—27 图9—289—5 图9—29所示电路正弦交流电路中,已知Ω=71R ,Ω=12R ,2=L H ,1=C F ,4=ωrad/s 。
求:(1)输入阻抗;(2)用两个串联元件等效时,元件的参数值;(3)用两个并联元件等效时,元件的参数值。
9—6 为确定电感线圈的参数R 和L ,用一只Ω1000电阻1R 与线圈并联,如图9—30所示,另以一电流表依次测得各支路的电流为:04.0=I A ,035.01=I A ,01.02=I A 。
已知Hz f 50=,试计算R 和L 。
图9—29 图9—309—7 如图9—31所示的电感线圈接到120=U V 的直流电源上时,电流为20A ,接到50=f Hz ,220=U V 的交流电源上时,电流为25A 。
求:线圈的R 和L 。
9—8 图9—32所示电路中,已知Ω=100R ,Hz f 50=,要使1U 和2U 间相位差为︒60,则C 应为多大?图9—31 图9—329—9 阻抗为Ω+=1.01.0j Z l 的输电线末端,接上10=P kW ,9.0cos =φ的感性负载,如图9—33所示,负载两端电压2202=U V 。
求:线路输入端的电压1U 及功率因数φcos 。
9—10 图—34所示正弦交流电路中,1,121=Ω==L R R H ,C 可变,10=ωrad/s 。
正弦稳态电路分析习题课正弦稳态电路分析习题课例1:i正弦稳态电路分析习题课例2:指出下列结果是否正确,若有错,试将其改正。
正弦稳态电路分析习题课i 正弦稳态电路分析习题课i s6正弦稳态电路分析习题课已知:电流表读数为1.5A(有效值)。
例5:正弦稳态电路分析习题课Ω40•I &正弦稳态电路分析习题课例6:已知:5ΩV )452sin(2)(o −=t t u 正弦稳态电路分析习题课I &Z 正弦稳态电路分析习题课例7:如图所示正弦稳态电路中,电流A 1、A 2的指示均为的读数。
满足KCL 的,相量满足o 01090j =o A o 452∠读数为14.1A正弦稳态电路分析习题课如图U =220V ,f =50H ,例8:•1I 正弦稳态电路分析习题课220U正弦稳态电路分析习题课例9:正弦稳态电路如图示,V1•正弦稳态电路分析习题课V1•正弦稳态电路分析习题课V1正弦稳态电路分析习题课例正弦稳态电路分析习题课正弦稳态电路分析习题课例12:设计RLC 带通滤波器电路,已知总电阻为正弦稳态电路分析习题课R L Cu s1u s2I&例11:如图所示电路,已知kHz 1210−Aμ142103106=×−正弦稳态电路分析习题课正弦稳态电路分析习题课例14:在串联谐振电路中电源内阻,电阻R代表线。
试求电阻R、电容C、。
Ω=1R 实际线圈模型正弦稳态电路分析习题课∴正弦稳态电路分析习题课设计电路,并计算互感线圈的各元件值。
当画耦合电感T型去耦等效电路时,若互感线圈两正弦稳态电路分析习题课据以上分析,所设计的互感电路(b)(a)正弦稳态电路分析习题课例16:P314 7-10求:i (t)和它的有效值I解:画出每一个频率分量的电路相量模型(0频率)(ω频率)50=I &)(&1⎟⎟⎞⎜⎜⎛正弦稳态电路分析习题课(3(9()()t t i ω6.17sin 74.135−+=o 正弦稳态电路分析习题课)V t ⎥⎦⎤ω2正弦稳态电路分析习题课0=I &0=∴U &。