经典习题平面法向量求法及应用
- 格式:doc
- 大小:2.01 MB
- 文档页数:8

法向量求法及应用方法法向量是指与一些曲面上的每一点的切平面垂直的向量。
在三维空间中,法向量可以方便地描述曲面的几何特征和方向。
一、法向量的求法:1.平面的法向量:平面的法向量可以通过两个不平行的向量叉积得到。
设平面上两个向量为a和b,法向量n=a×b。
2.曲面的法向量:曲面的法向量可以通过曲面的方程求得。
常见的曲面方程包括参数方程、隐函数方程和显函数方程。
对于参数方程和隐函数方程,可以通过求偏导数来得到曲面的切向量,然后再将切向量进行标准化得到法向量。
例如,对于参数方程x=x(u,v),y=y(u,v),z=z(u,v),法向量可以通过求∂(x,y,z)/∂(u,v)的叉积来得到。
而对于隐函数方程F(x,y,z)=0,可以通过对F(x,y,z)进行偏导数得到一个方程组,然后解这个方程组来得到法向量。
二、法向量的应用方法:1.曲面法向量的判定:通过计算曲面的法向量可以判断曲面的朝向和几何特征。
例如,在渲染图形时,可以通过曲面的法向量来决定光线对曲面的照射效果,以实现更真实的光影效果。
2.曲面法向量的插值和平滑:在计算机图形学中,通常需要对曲面进行插值和平滑处理。
曲面的法向量可以帮助我们在曲面上进行平滑采样。
例如,在曲面细分中,通过计算曲面的法向量来过滤掉尖锐的细分结果,使得细分结果更加平滑自然。
3.曲面的切平面和法向量的切线:对于空间曲线上的点,可以通过曲线的参数方程求得曲线的切线向量。
而对于空间曲面上的点,可以通过曲面的法向量和曲面上其中一点的切平面求得曲线的切向量。
切平面上的切向量和曲面的法向量垂直,并且与曲线相切。
4.计算曲面的面积和体积:曲面的法向量可以用来计算曲面的面积和体积。
对于平面,面积等于法向量的模长;对于曲面,可以通过对曲面分割成小区域然后计算每个小区域的法向量,并对法向量进行积分得到曲面的面积或体积。
5.平面和曲面的方程:法向量可以帮助我们确定平面和曲面的方程。
对于平面,通过平面上一点和法向量,可以得到平面的方程;对于曲面,通过曲面上一点和法向量,可以得到曲面的方程。



平面法向量的快速求解方法
咱先得知道啥是平面法向量。
简单说呢,平面法向量就是跟这个平面垂直的向量。
那咋求它呢?
有一种挺好用的方法哦。
假如说咱们有一个平面,这个平面是由两个不共线的向量确定的,比如说向量a和向量b。
那这个平面的法向量n就可以设成(x,y,z)。
然后呢,根据法向量和这两个向量都垂直的性质来列方程。
啥叫垂直呢?就是它们的点积为0呀。
那就是n·a = 0,n·b = 0。
这就得到了两个方程,像如果向量a =(a1,a2,a3),向量b =(b1,b2,b3),那就有a1x + a2y+ a3z = 0和b1x + b2y + b3z = 0。
这时候咋解呢?宝子们可别慌。
咱们可以给x或者y或者z先随便赋个值。
比如说,咱令x = 1,然后把这个值代入到那两个方程里,就变成了关于y和z的方程组啦。
解这个方程组就能求出y和z的值啦,这样法向量n就求出来了。
还有一种特殊情况呢。
要是这个平面在坐标轴上有特殊的关系,那求法向量就更简单了。
比如说平面平行于某一个坐标轴,那法向量在这个坐标轴方向上的分量就为0。
就像平面平行于x轴,那法向量就是(0,y,z)这种形式,再根据平面上的向量关系求出y和z就好啦。
宝子们,求解平面法向量其实没那么可怕,只要掌握了这些小技巧,就像找到了小捷径一样。
多做几道题,熟练了之后,一看到求平面法向量,心里就有底了,再也不会抓耳挠腮啦。
加油哦,宝子们,数学的小怪兽咱一个个打败!。

平面向量练习题及答案1. 向量初步概念和运算(1) 已知向量a=3i+4j,求向量a的模长。
答案:|a| = √(3^2 + 4^2) = 5(2) 已知向量b=-2i+5j,求向量b的模长。
答案:|b| = √((-2)^2 + 5^2) = √29(3) 已知向量c=2i+3j,求向量c的模长和方向角(与x轴正方向的夹角)。
答案:|c| = √(2^2 + 3^2) = √13方向角θ = arctan(3/2)2. 向量的线性运算(1) 已知向量a=3i+4j,向量b=-2i+5j,求向量a+b。
答案:a+b = (3-2)i + (4+5)j = i + 9j(2) 已知向量a=3i+4j,向量b=2i-7j,求向量a-b。
答案:a-b = (3-2)i + (4-(-7))j = i + 11j(3) 已知向量a=3i+4j,求向量-2a的模长。
答案:|-2a| = |-2(3i+4j)| = |-6i-8j| = √((-6)^2 + (-8)^2) = 103. 向量的数量积与投影(1) 已知向量a=3i+4j,向量b=-2i+5j,求向量a·b的值。
答案:a·b = (3*-2) + (4*5) = -6 + 20 = 14(2) 已知向量a=3i+4j,向量b=-2i+5j,求向量a在b方向上的投影。
答案:a在b方向上的投影= (a·b)/|b| = 14/√294. 向量的夹角和垂直判定(1) 判断向量a=3i+4j和向量b=-2i+5j是否相互垂直。
答案:两个向量相互垂直的条件是a·b = 0。
计算得到a·b = 14,因此向量a和向量b不相互垂直。
(2) 已知向量a=3i+4j,向量b=-8i+6j,求向量a和向量b的夹角。
答案:向量a和向量b的夹角θ = arccos((a·b)/(∣a∣*∣b∣)) = arccos((-66)/(√25*√100))5. 向量共线和平面向量的应用(1) 已知向量a=3i+4j,向量b=-6i-8j,判断向量a和向量b是否共线。

高三数学平面法向量的求法试题1.已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.(1)证明:⊥平面(2)求平面与平面所成角的余弦值;【答案】(1)通过建系证明,.得到,.故⊥平面.(2)二面角C-NB1-C1的余弦值为.【解析】(1)证明:∵该几何体的正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形,∴两两垂直.以分别为轴建立空间直角坐标系如图.则.∴,.∴,.又与相交于,∴⊥平面. ………6分(2)∵⊥平面,∴是平面的一个法向量,设为平面的一个法向量,则,所以可取.则.∴所求二面角C-NB1-C1的余弦值为. 12分【考点】本题主要考查立体几何中的垂直关系,角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离的计算。
证明过程中,往往需要将立体几何问题转化成平面几何问题加以解答。
本题解答,通过建立适当的空间直角坐标系,利用向量的坐标运算,简化了繁琐的证明过程,实现了“以算代证”,对计算能力要求较高。
2.如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC BD,垂足为H,PH是四棱锥的高,E为AD中点;(Ⅰ)证明:PE BC;(Ⅱ)若APB=ADB=60°,求直线PA与平面PEH所成角的正弦值。
【答案】(1)略(2)【解析】求解和证明立体几何问题一方面可以直接利用几何方法,通过证明或找到线面之间的关系,依据判定定理或性质进行证明求解.以为原点,分别为轴,线段的长为单位长,建立空间直角坐标系如图,则(Ⅰ)设则可得因为所以……………………5分(Ⅱ)由已知条件可得设为平面的法向量则即因此可以取,由,可得所以直线与平面所成角的正弦值为…………………12分3.如图,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB上一点(I) 当点E为AB的中点时,求证;BD1//平面A1DE(II)求点A1到平面BDD1的距离;(III) 当时,求二面角D1-EC-D的大小.【答案】(1)略(2)A1到面BDD1的距离为(3)D1-EC-D的大小为【解析】(I) 要证BD1//平面A1DE,只要证明BD1平行该面内的一条直线,取中点,由中位线可证得;(II)等积法求高;(III)可以用传统法找出平面角也可以向量法求。


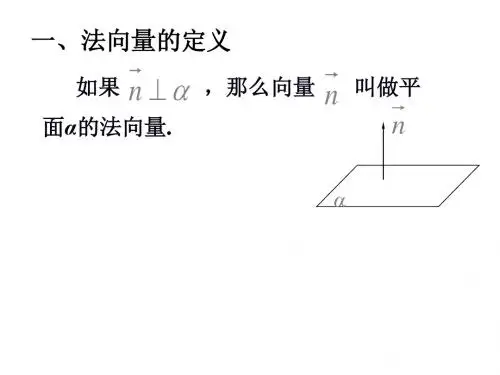
平面法向量的一种简单求法和在求角、距离中的应用一、法向量的定义:与平面垂直的向量叫平面的法向量(根据定义可知:平面的法向量有多个,方向有两种:向上或向下)二、向量的数量积a·b=∣a︳︳b∣cos<a,b>cos<a,b>=若a=(x1,y1,z1) b=(x2,y2,z2),则a·b= ∣a︳=三、向量积:a×ba×b的结果仍然是一个向量(使两个向量的起点相同)方向:右手手指指向a的方向,自然弯向b,则大拇指所指的方向就是向量a×b的方向(即:a×b垂直平面)大小:等于a,b为邻边的平行四边形的面积。
如图所示:(由此我们可以通过求两个向量的向量积求平面的法向量)a×b的坐标计算设a=(x1, y1, z1)b=(x2 , y2, z2)则:a×b =(︳y1y z1z︱,-︱x1x z1z︱,︱x1x y1y︱)其中:二阶行列式︱a b c d︱=ad-bc习惯上:作a×b时,把a写在上,把b写在下作b×a时,把b写在上,把a写在下练习:已知a=(2,1,0)b =(-1,2,1)(1)求a×b。
(2)求b×a解:a×b=b×a=注:根据上述分析要求一个平面的法向量,只要在平面内找出两个同起点的向量作向量积即可。
例:如图所示,正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是DD1、DC的中点。
求平面AEF的一个法向量解:以D∴A(E(F()∴AF=(AE=(∴平面AEF的法向量n=( )四、法向量在求角中的应用。
1、用法向量求线面角。
如图Θ=12π-<a,n> Θ=<a,n>- 12π两种情况下都有:sinΘ=︱cos<a,n>︱因为2、用法向量求二面角(2)如果两个平面的法向量选取合适,则二面角就等于两个平面的法向量的夹角(如第一种情况)。

法向量求法及应用方法法向量是指与平面或曲面相切且垂直于切平面或切曲面的向量。
在数学和物理领域中,法向量的求法和应用非常广泛。
本文将介绍法向量的求法以及在几何学、物理学和计算机图形学中的应用方法。
一、法向量的求法1.平面的法向量:给定平面方程Ax+By+Cz+D=0,其中A、B、C是平面的法向量的分量,可以直接读取得到。
这是最常见也是最简单的求法。
2.曲面的法向量:对于一般的曲面方程F(x,y,z)=0,其中F是曲面方程的函数,可以使用梯度算子求解法向量:-计算曲面方程在其中一点(x0,y0,z0)处的梯度矢量:∇F(x0,y0,z0)=(∂F/∂x,∂F/∂y,∂F/∂z),其中∂F/∂x、∂F/∂y、∂F/∂z是偏导数。
-梯度矢量就是曲面在该点处的法向量。
3.曲线的法向量:对于曲线方程F(t)=(x(t),y(t),z(t)),其中t是曲线的参数,可以使用导数求解法向量:-对曲线方程求导得到F'(t)=(x'(t),y'(t),z'(t)),其中x'(t)、y'(t)、z'(t)是曲线的导数。
-导数矢量就是曲线在该点处法向量的方向。
二、法向量的应用方法1.几何学中的应用:法向量是几何学中一个重要的概念,它可以用来判断两个平面或曲面的关系,如判断两个平面是否相交、平行或垂直。
在几何图形的旋转、平移和投影中,法向量也起到了重要的作用。
此外,法向量还可以用来计算曲面的面积和曲线的弯曲性等几何属性。
2.物理学中的应用:在物理学中,法向量有广泛的应用。
例如在力学中,力的方向可以通过物体表面的法向量来表示。
在光学中,光线的传播也可以通过曲面上的法向量来描述。
在电磁学中,电场和磁场的变化也可以通过法向量来表示。
法向量还可以用来计算曲面的斜率、曲率和高斯曲率等物理量。
3.计算机图形学中的应用:在计算机图形学中,法向量通常用于表达物体表面的方向,以便进行光照和着色计算。

平面法向量的 求法及其应用四川省华蓥中学 叶超本专题是我编写的一套书中的一篇,更多精彩,请参见我编写的那套书。
1、平面法向量的求法: 先来看看比较笨的方法。
(1)利用待定系数(参数)法,根据“平面的法向量⇔与平面内不共线的两向量均垂直的非零向量”及“两向量垂直⇔两向量的内积为0”确定待定参数。
例:已知四棱锥P —ABCD 的底面为直角梯形,AB//DC ,∠DAB =90°,PA ⊥底面ABCD ,且PA =AD =DC =21AB =1,M 是PB 的中点。
求面AMC 的一个法向量。
析:建系:以A 为原点,如图建立空间直角坐标系,则: 标点:A (0,0,0),C (1,1,0),P (0,0,1) B (0,2,0),M (0,1,1/2)列向量:AC =(1,1,0), AM =(0,1,1/2)待定参数法:设面AMC 的法向量为n =(x ,y ,z )于是n =(x ,-x ,2x )=x (1,-1,2) 其中,x 决定长度(和方向),可取n =(1,-1,2),它是图中的1n 还是2n 呢? 可用观察法确定:n =(1,-1,2)是以原点为起点、(1,-1,2)为终点的向量,是图中的1n 。
说明:这种方法虽能求解,但是:①要根据“两向量垂直⇔两向量的内积为0”列方程组并求解,计算量较大; ②利用观察法确定法向量的具体方向也不太方便。
综上,在高考的宝贵时间里,时间和精力都是很重要的,如果有一种方法可以很简便地求出平面的法向量,不仅可以节约时间,还可以节省精力,甚至提高准确度,那该多好啊!还真的有这种方法!这种方法不是我总结的,但如何用它来简便地求法向量却是我在半年前总结的,请看——A BPM D y =-x z =2x ⇒021=+=•z y AM n 0=+=•y x AC n(2)利用向量的矢量积求平面的法向量:(请重点看下面第②点中的第2个例题)①向量的矢量积的定义:向量a =(x 1,y 1,z 1)和b =(x 2,y 2,z 2)的矢量积=⨯b a (2211z y z y ,2211x z x z ,2211y x y x )=(y 1z 2-z 1y 2,z 1x 2-x 1z 2,x 1y 2-y 1x 2) 说明:2211z y z y 是二阶行列式,其值等于交叉相乘再相减(即:y 1z 2-z 1y 2),其余同理。
习题课 平面的法向量课时对点练1.直线l 的方向向量s =(-1,1,1),平面α的一个法向量为n =(2,x 2+x ,-x ),若直线l ∥α,则x 的值为( )A .-2B .- 2 C. 2 D .±2答案 D解析 由题意知,-1×2+1×(x 2+x )+1×(-x )=0,解得x =±2.2.已知点A (0,1,0),B (-1,0,-1),C (2,1,1),P (x ,0,z ),若P A ⊥平面ABC ,则点P 的坐标为( )A .(1,0,-2)B .(1,0,2)C .(-1,0,2)D .(2,0,-1)答案 C解析 由题意知AB →=(-1,-1,-1),AC →=(2,0,1),AP →=(x ,-1,z ),又P A ⊥平面ABC ,所以AB →·AP →=(-1,-1,-1)·(x ,-1,z )=0,得-x +1-z =0.①AC →·AP →=(2,0,1)·(x ,-1,z )=0,得2x +z =0,②联立①②得x =-1,z =2,故点P 的坐标为(-1,0,2).3.已知平面α的法向量是(2,3,-1),平面β的法向量是(4,λ,-2),若α∥β,则λ的值是( )A .-103B .6C .-6D .103答案 B解析 ∵α∥β,∴α的法向量与β的法向量也互相平行.∴24=3λ=-1-2(λ≠0),∴λ=6. 4.若平面α,β的法向量分别为u =(2,-3,5),v =(-3,1,-4),则( )A .α∥βB .α⊥βC .α,β相交但不垂直D .以上均不正确答案 C 5.(多选)若n 1,n 2分别是平面α,β的法向量,且α⊥β,n 1=(1,2,x ),n 2=(x ,x +1,x ),则x 的值为( )A .1B .2C .-1D .-2答案 CD解析 由题意可知,n 1·n 2=(1,2,x )·(x ,x +1,x )=x +2x +2+x 2=x 2+3x +2=0,解得x =-1或x =-2.6.(多选)已知v 为直线l 的方向向量,n 1,n 2分别为平面α,β的法向量(α,β不重合),那么下列说法中正确的有( )A .n 1∥n 2⇔α∥βB .n 1⊥n 2⇔α⊥βC .v ∥n 1⇔l ∥αD .v ⊥n 1⇔l ⊥α答案 AB解析 ∵平面α,β不重合,∴平面α,β的法向量平行等价于平面α,β 平行,∴A 正确;易知B 正确;当v ∥n 1时,l ⊥α,故C 错误;当v ⊥n 1时,l ∥α或l ⊂α,故D 错误.7.若平面α的一个法向量为v 1=(-3,y ,2),平面β的一个法向量为v 2=(6,-2,z ),且α∥β,则y +z =________.答案 -3解析 因为α∥β,所以v 1∥v 2, 所以-36=y -2=2z, 所以y =1,z =-4,所以y +z =-3.8.在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点.则平面AED 与A 1FD 1的位置关系是________.答案 垂直解析 如图,以点D 为坐标原点,分别以DA ,DC ,DD 1所在直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系Dxyz .设正方体的棱长为2,则D (0,0,0),A (2,0,0),E (2,2,1),F (0,1,0),A 1(2,0,2),D 1(0,0,2),∴DA →=D 1A 1—→=(2,0,0),DE →=(2,2,1),D 1F —→=(0,1,-2).设平面AED 的法向量为n 1=(x 1,y 1,z 1).由⎩⎪⎨⎪⎧ n 1·DA →=0,n 1·DE →=0, 得⎩⎪⎨⎪⎧2x 1=0,2x 1+2y 1+z 1=0. 令y 1=1,得n 1=(0,1,-2).同理,平面A 1FD 1的法向量为n 2=(0,2,1).∵n 1·n 2=(0,1,-2)·(0,2,1)=0,∴n 1⊥n 2,∴平面AED ⊥平面A 1FD 1.9.如图所示,△ABC 是一个正三角形,EC ⊥平面ABC ,BD ∥CE ,且CE =CA =2BD ,M 是EA 的中点.求证:平面DEA ⊥平面ECA .证明 以C 为原点,建立如图所示的空间直角坐标系Cxyz ,不妨设CA =2,则CE =2,BD =1,C (0,0,0),A (3,1,0),E (0,0,2),D (0,2,1).所以EA →=(3,1,-2),CE →=(0,0,2),ED →=(0,2,-1).分别设平面CEA 与平面DEA 的法向量为n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2),则⎩⎪⎨⎪⎧ n 1·EA →=0,n 1·CE →=0,即⎩⎨⎧ 3x 1+y 1-2z 1=0,2z 1=0,解得⎩⎨⎧ y 1=-3x 1,z 1=0. ⎩⎪⎨⎪⎧ n 2·EA →=0,n 2·ED →=0,即⎩⎨⎧ 3x 2+y 2-2z 2=0,2y 2-z 2=0,解得⎩⎨⎧x 2=3y 2,z 2=2y 2. 不妨取n 1=(1,-3,0),n 2=(3,1,2),因为n 1·n 2=0,所以两个法向量相互垂直,所以平面DEA ⊥平面ECA .10.如图所示,平面P AD ⊥平面ABCD ,四边形ABCD 为正方形,△P AD 是直角三角形,且P A =AD =2,E ,F ,G 分别是线段P A ,PD ,CD 的中点.求证:(1)PB ∥平面EFG ;(2)平面EFG ∥平面PBC .证明 (1)因为平面P AD ⊥平面ABCD ,且四边形ABCD 为正方形,所以AB ,AP ,AD 两两垂直.以A 为坐标原点,建立如图所示的空间直角坐标系Axyz ,则A (0,0,0),B (2,0,0),C (2,2,0),D (0,2,0),P (0,0,2),E (0,0,1),F (0,1,1),G (1,2,0).方法一 EF →=(0,1,0),EG →=(1,2,-1),设平面EFG 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧ n ·EF →=0,n ·EG →=0,即⎩⎪⎨⎪⎧y =0,x +2y -z =0, 令z =1,则n =(1,0,1)为平面EFG 的一个法向量,∵PB →=(2,0,-2),∴PB →·n =0,∴n ⊥PB →,∵PB ⊄平面EFG ,∴PB ∥平面EFG .方法二 PB →=(2,0,-2),FE →=(0,-1,0),FG →=(1,1,-1).设PB →=sFE →+tFG →,即(2,0,-2)=s (0,-1,0)+t (1,1,-1),∴⎩⎪⎨⎪⎧ t =2,t -s =0,-t =-2,解得s =t =2.∴PB →=2FE →+2FG →,又FE →与FG →不共线,∴PB →,FE →与FG →共面.∵PB ⊄平面EFG ,∴PB ∥平面EFG .(2)由(1)知,EF →=(0,1,0),BC →=(0,2,0),∴BC →=2EF →,∴BC ∥EF .又EF ⊄平面PBC ,BC ⊂平面PBC ,∴EF ∥平面PBC ,同理可证GF ∥PC ,从而得出GF ∥平面PBC .又EF ∩GF =F ,EF ⊂平面EFG ,GF ⊂平面EFG ,∴平面EFG ∥平面PBC .11.在三棱锥S -ABC 中,∠SAB =∠SAC =∠ACB =90°,AC =2,BC =13,SB =29,则直线SC 与BC 所成的角为( ) A .30° B .45° C .60° D .90°答案 D解析 如图,以A 为坐标原点,AC ,AS 所在直线分别为y 轴,z 轴建立空间直角坐标系Axyz ,则由AC =2,BC =13,SB =29,得B (-13,2,0),S (0,0,23),C (0,2,0),SC →=(0,2,-23),CB →=(-13,0,0).∵SC →·CB →=0,∴SC ⊥BC .∴SC 与BC 所成的角为90°.12.已知平面α内两向量a =(1,1,1),b =(0,2,-1)且c =m a +n b +(4,-4,1).若c 为平面α的法向量,则m ,n 的值分别为( )A .-1,2B .1,-2C .1,2D .-1,-2答案 A解析 c =m a +n b +(4,-4,1)=(m ,m ,m )+(0,2n ,-n )+(4,-4,1)=(m +4,m +2n -4,m -n +1),由c 为平面α的法向量,得⎩⎪⎨⎪⎧ c ·a =0,c ·b =0,得⎩⎪⎨⎪⎧m =-1,n =2. 13.已知平面α内的三点A (0,0,1),B (0,1,0),C (1,0,0),平面β的一个法向量为n =(-1,-1,-1),且β与α不重合,则( )A .α∥βB .α⊥βC .α与β相交但不垂直D .以上都不对答案 A解析 AB →=(0,1,-1),AC →=(1,0,-1),易知A ,B ,C 三点不共线,n ·AB →=-1×0+(-1)×1+(-1)×(-1)=0,n ·AC →=-1×1-1×0+(-1)×(-1)=0,∴n ⊥AB →,n ⊥AC →,∴n 也为α的一个法向量.又α与β不重合,∴α∥β.14.如图,四棱锥P -ABCD 的底面ABCD 是边长为1的正方形,PD ⊥底面ABCD ,且PD =1,若E ,F 分别为PB ,AD 的中点,则直线EF 与平面PBC 的位置关系是________.答案 垂直解析 以D 为原点,DA ,DC ,DP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系(图略), P (0,0,1),B (1,1,0),A (1,0,0),C (0,1,0),则E ⎝⎛⎭⎫12,12,12,F ⎝⎛⎭⎫12,0,0, ∴EF →=⎝⎛⎭⎫0,-12,-12,平面PBC 的一个法向量为n =(0,1,1). ∵EF →=-12n ,∴EF →∥n ,∴EF ⊥平面PBC .15.若正三棱锥P -ABC 侧面互相垂直,则棱锥的高与底面边长之比为________. 答案 1∶ 6 解析 设高为h ,底面边长为1,O 为△ABC 的中心,以O 为原点,建立如图所示空间直角坐标系,则P (0,0,h ),A ⎝⎛⎭⎫33,0,0,B ⎝⎛⎭⎫-36,12,0,C ⎝⎛⎭⎫-36,-12,0, P A →=⎝⎛⎭⎫33,0,-h ,PB →=⎝⎛⎭⎫-36,12,-h ,PC →=⎝⎛⎭⎫-36,-12,-h , 得平面P AB 的法向量n 1=⎝⎛⎭⎫3,3,1h , 平面P AC 的法向量n 2=⎝⎛⎭⎫3,-3,1h , 由平面P AB ⊥平面P AC ,知n 1⊥n 2,即n 1·n 2=0,得3-9+1h2=0, 解得h =66, 故高与底面边长之比为66∶1=6∶6=1∶ 6. 16.已知正方体ABCD -A 1B 1C 1D 1中,E 为棱CC 1上的动点.(1)求证:A 1E ⊥BD ;(2)若平面A 1BD ⊥平面EBD ,试确定E 点的位置.(1)证明 以D 为坐标原点,以DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系如图所示.设正方体棱长为a ,则B (a ,a ,0),D (0,0,0),A 1(a ,0,a ).设E (0,a ,e )(0≤e ≤a ).A 1E —→=(-a ,a ,e -a ),BD →=(-a ,-a ,0),A 1E —→·BD →=a 2-a 2+(e -a )·0=0,所以A 1E —→⊥BD →,即A 1E ⊥BD .(2)解 设平面A 1BD ,平面EBD 的法向量分别为n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2).因为DB →=(a ,a ,0),DA 1→=(a ,0,a ),DE →=(0,a ,e ),所以⎩⎪⎨⎪⎧ ax 1+ay 1=0,ax 1+az 1=0,⎩⎪⎨⎪⎧ax 2+ay 2=0,ay 2+ez 2=0. 取x 1=x 2=1,得n 1=(1,-1,-1),n 2=⎝⎛⎭⎫1,-1,a e . 由平面A 1BD ⊥平面EBD ,得n 1⊥n 2.所以2-a e =0,即e =a 2, 所以当E 为CC 1的中点时,平面A 1BD ⊥平面EBD .。
例谈平面法向量的求解方法及应用郭兴甫 云南会泽一中 邮编:654200平面法向量是空间向量中的一个重要内容,是解决立体几何问题的强有力工具,对解决线面平行,面面平行,二面角的大小,点面距离,线面角等问题具有公式化,程序化的作用,本文举例说明怎样求一个平面的法向量及其法向量在解决相关问题的应用,以期对同学们的学习有所帮助! 一、平面法向量的求解方法例1.在正方体1111D C B A ABCD -中,棱长为BC AB AA F E G a 、、分别为、、1,的中点,求平面GEF 的法向量.解:如图1所示,以D 为坐标原点建立空间 直角坐标系xyz D -,则)0,,2(),0,2,(a a F a a E ,),2,0,(a a G 由此得)0,2,2(),2,2,0(aa FE a a GE -=-=−→−−→−设平面GEF 的法向量为).,,(z y x n =−→−则由−→−−→−−→−−→−⊥⊥FE n GE n ,可得⎩⎨⎧==∴⎪⎪⎩⎪⎪⎨⎧=-=-⇒⎪⎩⎪⎨⎧=∙=∙−→−→−→−→,,,02121,0212100y x z y y x z y FE n GE n 令.1,1,1===x z y 则 故平面GEF 的一个法向量为).1,1,1(=−→−n评注:由上例可看出,在求平面α的法向量时,应建立空间直角坐标系,求 平面α内两个不共线的向量的坐标,并设平面α的一个法向量为).,,(z y x n =−→−由法向量的定义可知法向量必需与α内的向量垂直,进而得两个关于z y x ,,的三元一次方程令其中一个未知数为1,进而可得另两个未知数,即得平面的法向量→n .二、平面法向量的应用 1.证明两平面平行例2如图 2,已知正方体ABCD -A 1B 1C 1D 1中 E 、F 、G 、H 、M 、N 分别是正方体六个面的 中心,证明平面EFG//平面HMN证明:建立如图 2所示的空间直角坐 标系xyz D -,设正方体的棱长为2,易得:.)1,1,0(),1,2,1(),2,1,1(),1,1,2(),1,0,1(),0,1,1(N M H G F E .)1,0,1(),1,1,0(),1,0,1(),1,1,0(--=-==-=∴−→−−→−−→−−→−HN HM EG EF .设n 1=(x 1,y 1,z 1),n 2=(x ,y 2,z 2)分别是平面EFG ,平面HMN的法向量,则由 1,1,1,0,0111111111-===⎩⎨⎧=+=+-⇒⎪⎩⎪⎨⎧⊥⊥−→−→−→−→x y z z x z y EGn EFn 则令 所以平面EFG 的一个法向量)1,1,1(1-=→n同理由)1,1,1(,222-=⊥⊥→−→−→−→−→n HMN HN n HM n 的法向量可得平面→→→→=∴2121//,n n n n 即即平面E F G//平面HMN评注:证明两个平面平行可由以下方法去证明:(1)转化为相应的线线平行或线面平行,(2)求出两个平面的法向量,然后证明这两个平面的法向量平行而获证。
对平面法向量的专题探究平面法向量在处理线面角二面角以及距离等问题有着十分重要的用途,可以化繁为简,使立体几何中多年让师生感到头痛的问题迎刃而解现举例说明:利用平面法向量求线面角αA Bn φθABC DA B C D 1111xyz (图1)(图2)如图1,AB 为平面α的斜线,n αAB n ϕ与平面α之间所成的角为ϕπθ-=2,故欲求斜线AB 与平面α所成的角,只需求出向量AB 与平面α的法向量n 之间的夹角即可例题1如图2,在长方体1111D C B A ABCD -中,2,3,41===BB BC AB ,求直线B A 1和平面CD B A 11所成角的正弦值解:以D 为原点,以1,,DD DC DA 方向分别作为轴,y 轴,轴的正方向,则),2,4,3(),0,4,0(),2,0,3(),2,4,0(),0,4,0(),0,0,0(),0.4.3(),2,0,3(1111--===-=C A DC DA B A C D B A设平面CD B A 11的法向量),,(z y x n =,则⎪⎪⎩⎪⎪⎨⎧=⋅=⋅=⋅00011n C A n DC n DA ,即⎪⎩⎪⎨⎧=-+-==+024304023z y x y z x 故⎪⎩⎪⎨⎧-===302z y x 是其中一组解,即)3,0,2(-=n 为其中一个法向量,所以65653,cos 1=>=<n B A n B A ,故所求角的正弦值为65653利用平面法向量求二面角αβln 1n 2ABCD A B C D 1111xyz(图4)(图3)PQ 如图3,平面βα,的法向量21,n n 所成的角即为二面角βα--l 的平面角,注:当βα或半平面绕着其棱l 转动到与另一半平面重合时,这两个向量的方向应当一致例题2如图4,在正方体1111D C B A ABCD -中,Q P ,分别是AB AA ,1的中点,求平面PQ C 1和底面ABCD 所成角的余弦值解析:建立空间直角坐标系xyz D -,如图所示,由例题1的方法,容易求得平面1PQC 的法向量)2,2,3(1=n ,底面ABCD 的法向量)2,0,0(2=n ,所以17172,cos 21=>=<n n n n ,即为所求角的余弦值利用平面法向量求点到平面的距离yxzGFEAB CDαA P n(图5)(图6)如图5,求点P 到平面α的距离d ,可以在平面α上任意取一点A ,则><⋅=n AP d ,cos ,n 为平面α的法向量,方向如图例题3如图6,已知ABCD 是边长为4的正方形,F E ,分别是AD AB ,的中点,GC 是垂直于ABCD 所在的平面,且2=GC ,求点B 到平面EFG 的距离解:建立如图所示的空间直角坐标系xyz C -,则)0,4,0(),0,2,4(),0,4,2(B F E ,同例题1,容易求得平面EFG 的法向量)0,0,2(),1,31,31(-==EB n,11112311)1,31,31()0,0,2(,=⋅-===><=∴EB n EB n d 注:求线面距,面面距,可先转化为点面距,再用此法求解四、 利用平面法向量求异面直线的距离先设法求出同时与异面直线垂直的法向量n ,然后在两异面直线上分别任取点B A ,,则n AB d =><=,cos例题4已知正方体1111D C B A ABCD -的棱长为1,求直线AC DA 与1的距离ABCDxyz (图7)A 1B 1C 1D 1解析:建立坐标系xyz B -1,如图7所示,则点)1,1,0(),0,1,1(),1,0,0(),1,1,1(),0,0,1(),1,1,0(),1,0,1(111=-==D A AC A A D A C A 则,设),,(z y x n =为与D A AC 1与同时垂直的向量,即⎩⎨⎧=+=+-0z y y x ,故)1,1,1(-=n 为其中一个法向量,331111=++==d 所以直线AC DA 与1的距离为33。
平面法向量的应用例:(2009浙江,20)如图,平面PAC ⊥平面ABC ,ABC ∆是以AC 为斜边的等腰直角三角形,E 、F 、O 分别为PA 、PB 、AC 的中点,AC=16,PA=PC=10。
(1)设G 是OC 的中点,证明:F G ∥平面BOE ;(2)证明:在ABO 内存在一点M ,使FM ⊥平面BOE ,并求点M 到OA ,OB 的距离。
解:(1)如图,连OP ,以点O 为坐标原点,分别以OB 、OC 、OP 所在的直线为x 轴、y 轴、z 轴,建空间直角坐标系xyz O -。
易得)0,0,0(O ,)0,0,8(B ,)3,4,0(-E ,)3,0,4(F ,)0,4,0(G ,则)0,0,8(=OB ,)3,4,0(-=OE ,)3,4,4(--=FG , 设平面OBE 的法向量为),,(z y x n =,则有⎪⎩⎪⎨⎧=∙=∙0OE n OB n 即⎩⎨⎧=+-=03408z y x ,令4=z ,则3=y∴)4,3,0(=n又 01212=-=∙FG n 且直线FG 不在平面BOE 内, 所以F G ∥平面BOE 。
(2) 设点M 的坐标为)0,,(00y x ,则)3,,4(00--=y x FM 。
FM ⊥平面BOE ,B AEG POCFBAEGPOCFxy zFG ∴∥n ,则49,400-==y x ,即点M 的坐标为)0,49,4(-, 在平面直角坐标系xoy 中,AOB ∆的内部区域可表示为不等式组⎪⎩⎪⎨⎧<-<>800y x y x ,经检验点M 的坐标满足上述不等式组。
所以,在AOB ∆内存在一点M ,使FM ⊥平面BOE , 由点M 的坐标知,点M 到OA 、OB 的距离分别为4,49。
注:利用两平面的法向量之间的平行与垂直关系,进而可判两平面之间的平行与垂直关系,在此就不再举例说明了。
例:(2007全国I )四棱锥ABCD S -中,底面ABCD 为平行四边形,侧面SBC ⊥底面ABCD ,已知 45=∠ABC ,AB=2,22=BC ,3==SB SA 。
习题课 平面的法向量学习目标 1.熟练掌握求平面法向量的方法.2.会利用直线的方向向量及平面的法向量证明直线与平面平行、垂直,平面与平面平行、垂直. 一、利用空间向量证明线面平行例1 如图,在四棱锥P -ABCD 中,P A ⊥平面ABCD ,PB 与底面所成的角为45°,底面ABCD 为直角梯形,∠ABC =∠BAD =90°,P A =BC =12AD =1,问在棱PD 上是否存在一点E ,使CE ∥平面P AB ?若存在,求出E 点的位置;若不存在,请说明理由.解 由题意知,AB =P A ,以A 为原点,分别以AB ,AD ,AP 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系Axyz ,∴P (0,0,1),C (1,1,0),D (0,2,0), 设E (0,y ,z ),则PE →=(0,y ,z -1),PD →=(0,2,-1), ∵PE →∥PD →,∴(-1)×y -2(z -1)=0,①∵AD →=(0,2,0)是平面P AB 的法向量, 又CE →=(-1,y -1,z ),CE ∥平面P AB , ∴CE →⊥AD →,∴(-1,y -1,z )·(0,2,0)=0. ∴y =1,代入①得z =12,∴E 是PD 的中点,∴存在E 点,当点E 为PD 的中点时,CE ∥平面P AB .反思感悟 应用向量法证明线面平行问题的方法 (1)证明直线的方向向量与平面的法向量垂直.(2)证明直线的方向向量与平面内的某一直线的方向向量共线.(3)证明直线的方向向量可用平面内的任两个不共线的向量表示,即用平面向量基本定理证明线面平行.跟踪训练1 如图,在长方体ABCD -A 1B 1C 1D 1中,AD =AB =4,AA 1=2,点E ,F ,G 分别是DD 1,BD ,AA 1的中点,求证:D 1G ∥平面EFC .证明 方法一 如图,以D 为原点,DA →,DC →,DD 1—→所在的方向分别为x ,y ,z 轴正方向建立空间直角坐标系.则C (0,4,0),D 1(0,0,2),G (4,0,1),E (0,0,1),F (2,2,0), ∴D 1G —→=(4,0,-1),FE →=(-2,-2,1),FC →=(-2,2,0), 设平面EFC 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ⊥FE →,n ⊥FC →,∴⎩⎪⎨⎪⎧-2x -2y +z =0,-2x +2y =0.令x =1,解得y =1,z =4, ∴n =(1,1,4).又n ·D 1G —→=4×1+0×1+(-1)×4=0, ∴n ⊥D 1G —→.又D 1G ⊄平面EFC , ∴D 1G ∥平面EFC .方法二 取基底{DA →,DC →,DD 1—→}={a ,b ,c }, 由题意得EC →=ED →+DC →=-12c +b ,EF →=ED →+DF →=-12c +12a +12b ,GD 1→=GA 1→+A 1D 1—→=-a +12c ,设GD 1→=λEC →+v EF →.即-a +12c =λ⎝⎛⎭⎫-12c +b +v ⎝⎛⎭⎫-12c +12a +12b , 所以⎩⎪⎨⎪⎧-1=12v ,0=λ+12v ,12=-12λ-12v ,解得⎩⎪⎨⎪⎧λ=1,v =-2.即存在λ=1,v =-2,使GD 1→=EC →-2EF →, 即GD 1→,EC →,EF →共面.又GD 1⊄平面EFC ,所以GD 1∥平面EFC . 二、利用空间向量证明线面垂直例2 如图所示,正三棱柱ABC -A 1B 1C 1的所有棱长都为2,D 为CC 1的中点.求证:AB 1⊥平面A 1BD .证明 如图所示,取BC 的中点O ,连接AO . 因为△ABC 为正三角形,所以AO ⊥BC .因为在正三棱柱ABC -A 1B 1C 1中,平面ABC ⊥平面BCC 1B 1, 所以AO ⊥平面BCC 1B 1.取B 1C 1的中点O 1,以O 为原点,以OB →,OO 1→,OA →分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,则B (1,0,0),D (-1,1,0),A 1(0,2,3),A (0,0,3),B 1(1,2,0). 所以AB 1→=(1,2,-3),BA 1→=(-1,2,3),BD →=(-2,1,0).方法一 因为AB 1→·BA 1→=1×(-1)+2×2+(-3)×3=0,AB 1→·BD →=1×(-2)+2×1+(-3)×0=0,所以AB 1→⊥BA 1→,AB 1→⊥BD →,即AB 1⊥BA 1,AB 1⊥BD .又因为BA 1∩BD =B ,BA 1,BD ⊂平面A 1BD , 所以AB 1⊥平面A 1BD .方法二 设平面A 1BD 的法向量为n =(x ,y ,z ), 则有n ⊥BA 1→,n ⊥BD →,故⎩⎪⎨⎪⎧n ·BA 1→=0,n ·BD →=0⇒⎩⎨⎧-x +2y +3z =0,-2x +y =0,令x =1,则y =2,z =-3,故n =(1,2,-3)为平面A 1BD 的一个法向量, 又AB 1→=(1,2,-3),所以AB 1→=n , 所以AB 1→∥n ,故AB 1⊥平面A 1BD .反思感悟 用坐标法证明线面垂直的方法及步骤 方法一:(1)建立空间直角坐标系. (2)将直线的方向向量用坐标表示.(3)找出平面内两条相交直线,并用坐标表示它们的方向向量. (4)分别计算两组向量的数量积,得到数量积为0. 方法二:(1)建立空间直角坐标系. (2)将直线的方向向量用坐标表示. (3)求出平面的法向量.(4)判断直线的方向向量与平面的法向量平行.跟踪训练2 如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC =60°,P A =AB =BC =2,E 是PC 的中点,求证:(1)CD ⊥AE ; (2)PD ⊥平面ABE .证明 (1)以A 为坐标原点,AB ,AD ,AP 所在的直线分别为x ,y ,z 轴,建立如图所示的空间直角坐标系,则A (0,0,0),B (2,0,0),C (1,3,0),D ⎝⎛⎭⎫0,433,0,P (0,0,2),E ⎝⎛⎭⎫12,32,1,所以CD →=⎝⎛⎭⎫-1,33,0,AE →=⎝⎛⎭⎫12,32,1,所以CD →·AE →=-1×12+33×32+0×1=0,所以CD ⊥AE .(2)由(1),得PD →=⎝⎛⎭⎫0,433,-2,AB →=(2,0,0),AE →=⎝⎛⎭⎫12,32,1,设向量n =(x ,y ,z )是平面ABE 的法向量,则 由⎩⎪⎨⎪⎧ n ·AB →=0,n ·AE →=0,得⎩⎪⎨⎪⎧2x =0,12x +32y +z =0, 取y =2,则n =(0,2,-3), 所以PD →=233n ,所以PD ∥n ,所以PD ⊥平面ABE .三、利用空间向量证明面面平行例3 如图,在正方体ABCD -A 1B 1C 1D 1中,O 是底面ABCD 的中心,P 是DD 1的中点.设Q 是CC 1上的点,当点Q 在什么位置时,平面D 1BQ ∥平面P AO ?解 以D 为原点,DA →,DC →,DD 1—→的方向分别为x 轴,y 轴,z 轴正方向,建立如图所示的空间直角坐标系Dxyz ,设正方体的棱长为2,则O (1,1,0),A (2,0,0),P (0,0,1),B (2,2,0).设Q (0,2,c ),∴OA →=(1,-1,0),OP →=(-1,-1,1),BQ →=(-2,0,c ). 设平面P AO 的法向量为n 1=(x ,y ,z ),则⎩⎪⎨⎪⎧n 1·OA →=0,n 1·OP →=0⇒⎩⎪⎨⎪⎧x -y =0,-x -y +z =0,令x =1,则y =1,z =2,∴平面P AO 的一个法向量为n 1=(1,1,2). 若平面D 1BQ ∥平面P AO ,则n 1也是平面D 1BQ 的一个法向量. ∴n 1·BQ →=0,即-2+2c =0,∴c =1,故当Q 为CC 1的中点时,平面D 1BQ ∥平面P AO . 反思感悟 证明面面平行的方法设平面α的法向量为n 1=(a 1,b 1,c 1),平面β的法向量为n 2=(a 2,b 2,c 2),则α∥β⇔n 1∥n 2⇔(a 1,b 1,c 1)=k (a 2,b 2,c 2)(k ∈R ).跟踪训练3 已知正方体ABCD -A 1B 1C 1D 1的棱长为2,E ,F 分别是BB 1,DD 1的中点. 求证:平面ADE ∥平面B 1C 1F .证明 以D 为原点,DA →,DC →,DD 1—→的方向分别为x 轴,y 轴,z 轴的正方向,建立如图所示的空间直角坐标系Dxyz ,则有D (0,0,0),A (2,0,0),C (0,2,0),C 1(0,2,2),E (2,2,1),F (0,0,1),B 1(2,2,2),∴DA →=(2,0,0),AE →=(0,2,1). 设n 1=(x 1,y 1,z 1)是平面ADE 的法向量, 则n 1⊥DA →,n 1⊥AE →,即⎩⎪⎨⎪⎧n 1·DA →=2x 1=0,n 1·AE →=2y 1+z 1=0,得⎩⎪⎨⎪⎧x 1=0,z 1=-2y 1,令z 1=2,则y 1=-1, 所以n 1=(0,-1,2).因为C 1B 1—→=(2,0,0),FC 1→=(0,2,1), 设n 2=(x 2,y 2,z 2)是平面B 1C 1F 的法向量. 由n 2⊥FC 1→,n 2⊥C 1B 1—→,得⎩⎪⎨⎪⎧n 2·FC 1→=2y 2+z 2=0,n 2·C 1B 1—→=2x 2=0,得⎩⎪⎨⎪⎧x 2=0,z 2=-2y 2.令z 2=2,得y 2=-1,所以n 2=(0,-1,2), 因为n 1=n 2,所以平面ADE ∥平面B 1C 1F . 四、利用空间向量证明面面垂直例4 三棱锥被平行于底面ABC 的平面所截得的几何体如图所示,截面为A 1B 1C 1,∠BAC =90°,A 1A ⊥平面ABC ,A 1A =3,AB =AC =2A 1C 1=2,D 为BC 的中点.证明:平面A 1AD ⊥平面BCC 1B 1.证明 方法一 如图,以点A 为坐标原点,AB ,AC ,AA 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Axyz ,则A (0,0,0),B (2,0,0),C (0,2,0),A 1(0,0,3),C 1(0,1,3). ∵D 为BC 的中点,∴D 点坐标为(1,1,0),∴AD →=(1,1,0),AA 1→=(0,0,3),BC →=(-2,2,0), ∴AD →·BC →=1×(-2)+1×2+0×0=0, AA 1→·BC →=0×(-2)+0×2+3×0=0, ∴AD →⊥BC →,AA 1→⊥BC →, ∴BC ⊥AD ,BC ⊥AA 1.又A 1A ∩AD =A ,A 1A ,AD ⊂平面A 1AD , ∴BC ⊥平面A 1AD . 又BC ⊂平面BCC 1B 1, ∴平面A 1AD ⊥平面BCC 1B 1.方法二 同方法一建系后,得AA 1→=(0,0,3),AD →=(1,1,0),BC →=(-2,2,0),CC 1→=(0,-1,3). 设平面A 1AD 的法向量为n 1=(x 1,y 1,z 1),平面BCC 1B 1的法向量为n 2=(x 2,y 2,z 2). 由⎩⎪⎨⎪⎧n 1·AA 1→=0,n 1·AD →=0,得⎩⎨⎧3z 1=0,x 1+y 1=0,令y 1=-1,则x 1=1,z 1=0, ∴n 1=(1,-1,0).由⎩⎪⎨⎪⎧n 2·BC →=0,n 2·CC 1→=0,得⎩⎨⎧-2x 2+2y 2=0,-y 2+3z 2=0,令y 2=1,则x 2=1,z 2=33, ∴n 2=⎝⎛⎭⎫1,1,33. ∵n 1·n 2=1-1+0=0,∴n 1⊥n 2, ∴平面A 1AD ⊥平面BCC 1B 1.反思感悟 利用空间向量证明面面垂直通常可以有两个途径,一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直;二是直接求解两个平面的法向量,证明两个法向量垂直,从而得到两个平面垂直.跟踪训练4 如图,在正三棱柱ABC -A 1B 1C 1中,AB =13AA 1=a ,E ,F 分别是BB 1,CC 1上的点,且BE =a ,CF =2a ,求证:平面AEF ⊥平面ACF .证明 以A 为坐标原点,建立如图所示的空间直角坐标系Axyz ,不妨设a =2,则A (0,0,0),E (3,1,2),F (0,2,4), ∴AE →=(3,1,2),AF →=(0,2,4).∵x 轴⊥平面ACF ,∴可取平面ACF 的一个法向量为m =(1,0,0).设平面AEF 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·AE →=3x +y +2z =0,n ·AF →=2y +4z =0,取z =1,得n =(0,-2,1). ∵m ·n =0,∴m ⊥n , ∴平面AEF ⊥平面ACF .1.知识清单:(1)利用空间向量证明线面平行. (2)利用空间向量证明线面垂直. (3)利用空间向量证明面面平行. (4)利用空间向量证明面面垂直. 2.方法归纳:数形结合、转化与化归.3.常见误区:直线的方向向量与平面的法向量垂直时,线面关系有两种,即线与面平行或线在面内,线在面内这种情况容易忽视.1.直线l 的一个方向向量为(2,4,5),平面α的一个法向量为(1,2,t ),若l ⊥α,则实数t 等于( )A.52 B .1 C .-2 D .-85 答案 A解析 因为l ⊥α,所以直线l 的方向向量与平面的法向量平行, 可得21=42=5t (t ≠0),解得t =52.2.若两个不同平面α,β的法向量分别为u =(1,2,-1),v =(-3,-6,3),则( ) A .α∥β B .α⊥β C .α,β相交但不垂直 D .以上均不正确 答案 A解析 ∵v =-3u ,∴v ∥u .故α∥β.3.已知平面α和平面β的法向量分别为a =(1,1,2),b =(x ,-2,3),且α⊥β,则x 等于( )A .-4B .-8C .4D .8 答案 A解析 因为a ·b =x -2+6=0,所以x =-4.4.如图所示,在正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M ,N 分别为A 1B 和AC 上的点,A 1M =AN =2a3,则MN 与平面BB 1C 1C 的位置关系是________.答案 平行解析 以C 1为原点,建立如图所示的空间直角坐标系,由于A 1M =AN =2a 3, 则M ⎝⎛⎭⎫a ,2a 3,a 3,N ⎝⎛⎭⎫2a 3,2a 3,a ,MN →=⎝⎛⎭⎫-a 3,0,2a 3. 又C 1D 1⊥平面BB 1C 1C ,所以C 1D 1—→=(0,a ,0)为平面BB 1C 1C 的一个法向量. 因为MN →·C 1D 1—→=0, 所以MN →⊥C 1D 1—→, 又MN ⊄平面BB 1C 1C , 所以MN ∥平面BB 1C 1C .。
巧求平面法向量在空间直角坐标系中,平面的一般方程是0d cz by ax =+++(其中系数a,b,c 不同时为零),则向量)c ,b ,a (n =→为平面0d cz by ax =+++的法向量。
根据这一原理,我们可以按下列方法求平面的法向量。
定理1:若平面α不经过原点.....,,取平面α内不共线的三点A 、B 、C ,将其分别坐标代入关于z y x ,,的方程1cz by ax =++(等号右边的1也可以是其它任意非零常数),求出系数a,b,c 的一组值,则向量)c ,b ,a (n =→为平面α的法向量定理2:若平面α经过原点....,取平面α内与原点不共线的两点A 、B ,将其坐标代入关于z y x ,,的方程0cz by ax =++,求出系数a,b,c 的一组值,则向量)c ,b ,a (n =→为平面α的法向量。
例1:已知如图正四棱柱ABCD -A 1B 1C 1D 1的棱长AA 1=2,AB=1,按图中所建立的坐标系,求平面BDC 1,平面A 1BC 1,平面ABC 1D 1的法向量。
解(1)因为平面BDC 1过原点D,将点B(1,1,0),C 1(0,1,2)代入0cz by ax =++得:020a b b c +=⎧⎨+=⎩所以2a bb c=-⎧⎨=-⎩。
不妨设c=1,可得b=-2, a=2。
所以)1,2,2(n -=→是平面BDC 1的法向量 (2)因为平面A 1BC 1不过原点D,将点A 1(1,0,2),B (1,1,0)C 1(0,1,2)代入1cz by ax =++得:21121a c a b b c +=⎧⎪+=⎨⎪+=⎩所以121214a b c ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩所以)41,21,21(n =→为平面BDC 1的法向量 (3) 因为平面ABC 1D 1不过原点D,将A 1(1,0,2),B (1,1,0C 1(0,0,2)代入1代入2ax by cz ++=得22022221a c a a b b c c +==⎧⎧⎪⎪+==⎨⎨⎪⎪==⎩⎩即所以(0,2,1)n →=是平面ABC 1D 1的法向量。