3.2.2平面的法向量与平面的向量表示

平面向量与平面的关系平面向量是向量的一种形式，它的组成部分是一个起点和一个终点，可以用箭头来表示。

平面是二维的，由二维点的集合构成，其上的点可以用二维坐标表示。

本文将探讨平面向量与平面之间的关系及相关的性质。

一、平面向量的定义与性质平面向量可以表示为两个点之间的差向量。

设点A(x1, y1)和点B(x2, y2)是平面上的两个点，其联结的平面向量可以表示为AB = (x2 -x1, y2 - y1)。

平面向量具有以下性质：1. 平面向量的模：平面向量AB的模可以通过勾股定理求得，即|AB| = √[(x2 - x1)^2 + (y2 - y1)^2]。

2. 平面向量的加法：两个平面向量的加法可以通过将它们的对应分量相加得到。

设平面向量A(x1, y1)和平面向量B(x2, y2)，它们的和为A +B = (x1 + x2, y1 + y2)。

3. 平面向量的数量积：两个平面向量的数量积定义为它们对应分量的乘积的和。

设平面向量A(x1, y1)和平面向量B(x2, y2)，它们的数量积为A · B = x1x2 + y1y2。

4. 平面向量的夹角：设平面向量A和平面向量B不同时为零向量，它们的夹角θ可以由余弦定理求得，即cosθ = (A · B) / (|A| |B|)，从而可以计算出夹角的大小。

二、平面向量与平面之间的关系平面向量和平面之间有着密切的关系，我们将讨论以下几个方面：1. 平面上的平行向量：若两个平面向量的方向相同或相反，它们为平行向量。

若平面向量A(a, b)与平面向量B(x, y)平行，则存在实数k，使得a = kx，b = ky。

2. 平面上的法向量：设平面向量A(a, b)与平面向量B(x, y)垂直，则A为平面的法向量。

当且仅当a = -ky，b = kx时，平面向量A与平面向量B垂直。

3. 平面与平面之间的夹角：设平面P1的法向量为A(a1, b1)，平面P2的法向量为B(a2, b2)，则两个平面之间的夹角θ可以由以下公式计算得到：cosθ = (a1a2 + b1b2) / (|A| |B|)。

（人教课标版）普通高中课程标准实验教科书《数学》目录（B版）（人教课标版）普通高中课程标准实验教科书《数学》目录（B版）必修一第一章集合1.1集合与集合的表示方法1.1.1集合的概念1.1.2集合的表示方法1.2集合之间的关系与运算1.2.1集合之间的关系1.2.2集合的运算本章小结阅读与欣赏聪明在于学习，天才由于积累第二章函数2.1函数2.1.1函数2.1.2函数的表示方法2.1.3函数的单调性2.1.4函数的奇偶性2.1.5用计算机作函数的图象（选学）2.2一次函数和二次函数2.2.1一次函数的性质与图象2.2.3待定系数法2.3函数的应用（Ⅰ）2.4函数与方程2.4.1函数的零点2.4.2求函数零点近似解的一种计算方法——二分法本章小结阅读与欣赏函数概念的形成与发展第三章基本初等函数（Ⅰ）3.1指数与指数函数3.1.1实数指数幂及其运算3.1.2指数函数3.2对数与对数函数3.2.1对数及其运算3.2.2对数函数3.2.3指数函数与对数函数的关系3.3幂函数3.4函数的应用（Ⅱ）本章小结阅读与欣赏对数的发明必修二第一章立体几何初步1.1空间几何体1.1.1构成空间几何体的基本元素1.1.2棱柱、棱锥和棱台的结构特征1.1.3圆柱、圆锥、圆台和球1.1.4投影与直观图1.1.5三视图1.1.6棱柱、棱锥、棱台和球的表面积1.1.7柱、锥、台和球的体积实习作业1.2点、线、面之间的位置关系1.2.1平面的基本性质与推论1.2.2空间中的平行关系1.2.3空间中的垂直关系本章小结阅读与欣赏散发着数学芳香的碑文第二章平面解析几何初步2.1平面直角坐标系中的基本公式2.1.1数轴上的基本公式2.1.2平面直角坐标系中的基本公式2.2直线的方程2.2.1直线方程的概念与直线的斜率2.2.2直线方程的几种形式2.2.3两条直线的位置关系2.2.4点到直线的距离2.3圆的方程2.3.1圆的标准方程2.3.2圆的一般方程2.3.3直线与圆的位置关系2.3.4圆与圆的位置关系2.4空间直角坐标系2.4.1空间直角坐标系2.4.2空间两点的距离公式本章小结阅读与欣赏笛卡儿必修三第一章算法初步1.1算法与程序框图1.1.1算法的概念1.1.2程序框图1.1.3算法的三种基本逻辑结构和框图表示1.2基本算法语句1.2.1赋值、输入和输出语句1.2.2条件语句1.2.3循环语句1.3中国古代数学中的算法案例本章小结阅读与欣赏我国古代数学家秦九韶附录1解三元一次方程组的算法、框图和程序附录2Scilab部分函数指令表第二章统计2.1随机抽样2.1.2系统抽样2.1.4数据的收集2.2用样本估计总体2.2.1用样本的频率分布估计总体的分布2.2.2用样本的数字特征估计总体的数字特征2.3变量的相关性2.3.1变量间的相关关系2.3.2两个变量的线性相关本章小结阅读与欣赏蚂蚁和大象谁的力气更大附录随机数表第三章概率3.1事件与概率3.1.1随机现象3.1.2事件与基本事件空间3.1.3频率与概率3.1.4概率的加法公式3.2古典概型3.2.1古典概型3.2.2概率的一般加法公式（选学）3.3随机数的含义与应用3.3.1几何概型3.3.2随机数的含义与应用3.4概率的应用本章小结阅读与欣赏概率论的起源必修四第一章基本初等函数（Ⅱ）1.1任意角的概念与弧度制1.1.1角的概念的推广1.1.2弧度制和弧度制与角度制的换算1.2任意角的三角函数1.2.1三角函数的定义1.2.2单位圆与三角函数线1.2.3同角三角函数的基本关系式1.2.4诱导公式1.3三角函数的图象与性质1.3.1正弦函数的图象与性质1.3.2余弦函数、正切函数的图象与性质1.3.3已知三角函数值求角教学建模活动本章小结阅读与欣赏三角学的发展第二章平面向量2.1向量的线性运算2.1.1向量的概念2.1.2向量的加法2.1.3向量的减法2.1.4数乘向量2.1.5向量共线的条件与轴上向量坐标运算2.2向量的分解与向量的坐标运算2.2.1平面向量基本定理2.2.2向量的正交分解与向量的直角坐标运算2.2.3用平面向量坐标表示向量共线条件2.3平面向量的数量积2.3.1向量数量积的物理背景与定义2.3.2向量数量积的运算律2.3.3向量数量积的坐标运算与度量公式2.4向量的应用2.4.1向量在几何中的应用2.4.2向量在物理中的应用本章小结阅读与欣赏向量概念的推广与应用第三章三角恒等变换3.1和角公式3.1.1两角和与差的余弦3.1.2两角和与差的正弦3.1.3两角和与差的正切3.2倍角公式和半角公式3.2.1倍角公式3.2.2半角的正弦、余弦和正切3.3三角函数的积化和差与和差化积本章小结阅读与欣赏和角公式与旋转对称必修五第一章解三角形1.1正弦定理和余弦定理1.1.1正弦定理1.1.2余弦定理1.2应用举例本章小结阅读与欣赏亚历山大时期的三角测量第二章数列2.1数列2.1.1数列2.1.2数列的递推公式（选学）2.2等差数列2.2.1等差数列2.2.2等差数列的前n项和2.3等比数列2.3.1等比数列2.3.2等比数列的前n项和本章小结阅读与欣赏级数趣题无穷与悖论第三章不等式3.1不等关系与不等式3.1.1不等关系与不等式3.1.2不等式的性质3.2均值不等式3.3一元二次不等式及其解法3.4不等式的实际应用3.5二元一次不等式（组）与简单的线性规划问题3.5.1二元一次不等式（组）所表示的平面区域3.5.2简单线性规划本章小结选修1-1第一章常用逻辑用语1.1命题与量词1.1.1命题1.1.2量词1.2基本逻辑联结词1.2.1“且”与“或”1.2.2“非”（否定）1.3充分条件、必要条件与命题的四种形式1.3.1推出与充分条件、必要条件1.3.2命题的四种形式本章小结阅读与欣赏什么是数理逻辑第二章圆锥曲线与方程2.1椭圆2.1.1椭圆及其标准方程2.1.2椭圆的几何性质2.2双曲线2.2.1双曲线及其标准方程2.2.2双曲线的几何性质2.3抛物线2.3.1抛物线级其标准方程2.3.2抛物线的几何性质本章小结阅读与欣赏圆锥面与圆锥曲线第三章导数及其应用3.1导数3.1.1函数的平均变化率3.1.2瞬时速度与导数3.1.3导数的几何意义3.2导数的运算3.2.1常数与幂函数的导数3.2.2导数公式表3.2.3导数的四则运算法则3.3导数的应用3.3.1利用导数判断函数的单调性3.3.2利用导数研究函数的极值3.3.3导数的实际应用本章小结阅读与欣赏微积分与极限思想选修1-2第一章统计案例1.1独立性检验1.2回归分析本章小结“回归”一词的由来附表相关性检验的临界值表第二章推理与证明2.1合情推理与演绎推理2.1.1合情推理2.1.2演绎推理2.2直接证明与间接证明2.2.1综合法与分析法2.2.2反证法本章小结阅读与欣赏《原本》与公理化思想数学证明的机械化——机器证明第三章数系的扩充与复数的引入3.1数系的扩充与复数的引入3.1.1实数系3.1.2复数的引入3.2复数的运算3.2.1复数的加法和减法3.2.2复数的乘法和除法本章小结复平面与高斯第四章框图4.1流程图4.2结构图本章小结阅读与欣赏冯·诺伊曼选修2-1第一章常用逻辑用语1.1命题与量词1.1.1命题1.1.2量词1.2基本逻辑联结词1.2.1“且”与“或”1.2.2“非”（否定）1.3充分条件、必要条件与命题的四种形式1.3.1推出与充分条件、必要条件本章小结阅读与欣赏什么是数理逻辑第二章圆锥曲线与方程2.1曲线与方程2.1.1曲线与方程的概念2.1.2由曲线求它的方程、由方程研究曲线的性质2.2椭圆2.2.1椭圆的标准方程2.2.2椭圆的几何性质2.3双曲线2.3.1双曲线的标准方程2.3.2双曲线的几何性质2.4抛物线2.4.1抛物线的标准方程2.4.2抛物线的几何性质2.5直线与圆锥曲线本章小结阅读与欣赏圆锥面与圆锥曲线第三章空间向量与立体几何3.1空间向量及其运算3.1.1空间向量的线性运算3.1.2空间向量的基本定理3.1.3两个向量的数量积3.1.4空间向量的直角坐标运算3.2空间向量在立体几何中的应用3.2.1直线的方向向量与直线的向量方程3.2.2平面的法向量与平面的向量表示3.2.3直线与平面的夹角3.2.4二面角及其度量3.2.5距离（选学）本章小结阅读与欣赏向量的叉积及其性质选修2-2第一章导数及其应用1.1导数1.1.1函数的平均变化率1.1.2瞬时速度与导数1.1.3导数的几何意义1.2导数的运算1.2.1常数函数与冥函数的导数1.2.2导数公式表及数学软件的应用1.2.3导数的四则运算法则1.3导数的应用1.3.1利用导数判断函数的单调性1.3.2利用导数研究函数的极值1.3.3导数的实际应用1.4定积分与微积分基本定理1.4.1曲边梯形面积与定积分1.4.2微积分基本定理本章小结阅读与欣赏微积分与极限思想第二章推理与证明2.1合情推理与演绎推理2.1.1合情推理2.1.2演绎推理2.2直接证明与间接证明2.2.1综合法与分析法2.2.2反证法2.3数学归纳法2.3.1数学归纳法2.3.2数学归纳法应用举例本意小结阅读与欣赏《原本》与公理化思想第三章数系的扩充与复数3.1数系的扩充与复数的概念3.1.1实数系3.1.2复数的概念3.1.3复数的几何意义3.2复数的运算3.2.1复数的加法与减法3.2.2复数的乘法3.2.3复数的除法本章小节阅读与欣赏复平面与高斯选修2-3第一章计数原理1.1基本计数原理1.2排列与组合1.2.1排列1.2.2组合1.3二项式定理1.3二项式定理1.3.2杨辉三角本章小结第二章概率2.1离散型随机变量及其分布列2.1.1离散型随机变量2.1.2离散型随机变量的分布列2.1.3超几何分布2.2条件概率与事件的独立性2.2.1条件概率2.2.2事件的独立性2.2.3独立重复试验与二项分布2.3随机变量的数字特征2.3.1离散型随机变量的数学期望2.3.2离散型随机变量的方差2.4正态分布本章小结阅读与欣赏关于“玛丽莲问题”的争论第三章统计案例3.1独立性检验3.2回归分析本章小结阅读与欣赏“回归”一词的由来附表选修3-1第一讲早期的算术与几何一古埃及的数学二两河流域的数学三丰富多彩的记数制度第二讲古希腊数学一希腊数学的先行者二毕达哥拉斯学派三欧几里得与《原本》四数学之神──阿基米德第三讲中国古代数学瑰宝一《周髀算经》与赵爽弦图二《九章算术》三大衍求一术四中国古代数学家第四讲平面解析几何的产生一坐标思想的早期萌芽二笛卡儿坐标系三费马的解析几何思想四解析几何的进一步发展第五讲微积分的诞生一微积分产生的历史背景二科学巨人牛顿的工作三莱布尼茨的“微积分”第六讲近代数学两巨星一分析的化身──欧拉二数学王子──高斯第七讲千古谜题一三次、四次方程求根公式的发现二高次方程可解性问题的解决三伽罗瓦与群论四古希腊三大几何问题的解决第八讲对无穷的深入思考一古代的无穷观念二无穷集合论的创立三集合论的进一步发展与完善第九讲中国现代数学的开拓与发展一中国现代数学发展概观二人民的数学家──华罗庚三当代几何大师──陈省身选修3-2暂缺选修3-3第一讲从欧氏几何看球面一平面与球面的位置关系二直线与球面的位置关系和球幂定理三球面的对称性第二讲球面上的距离和角一球面上的距离二球面上的角第三讲球面上的基本图形一极与赤道二球面二角形三球面三角形1．球面三角形2．三面角3．对顶三角形4．球极三角形第四讲球面三角形一球面三角形三边之间的关系二、球面“等腰”三角形三球面三角形的周长四球面三角形的内角和第五讲球面三角形的全等1．“边边边”(s.s.s)判定定理2．“边角边”(s.a.s.)判定定理3．“角边角”(a.s.a.)判定定理4．“角角角”(a.a.a.)判定定理第六讲球面多边形与欧拉公式一球面多边形及其内角和公式二简单多面体的欧拉公式三用球面多边形的内角和公式证明欧拉公式第七讲球面三角形的边角关系一球面上的正弦定理和余弦定理二用向量方法证明球面上的余弦定理1．向量的向量积2．球面上余弦定理的向量证明三从球面上的正弦定理看球面与平面四球面上余弦定理的应用──求地球上两城市间的距离第八讲欧氏几何与非欧几何一平面几何与球面几何的比较二欧氏平行公理与非欧几何模型──庞加莱模型三欧氏几何与非欧几何的意义阅读与思考非欧几何简史选修3-4第一讲平面图形的对称群一平面刚体运动1．平面刚体运动的定义2．平面刚体运动的性质二对称变换1．对称变换的定义2．正多边形的对称变换3．对称变换的合成4．对称变换的性质5．对称变换的逆变换三平面图形的对称群第二讲代数学中的对称与抽象群的概念一n元对称群Sn二多项式的对称变换三抽象群的概念1．群的一般概念2．直积第三讲对称与群的故事一带饰和面饰二化学分子的对称群三晶体的分类四伽罗瓦理论选修4-1第一讲相似三角形的判定及有关性质一平行线等分线段定理二平行线分线段成比例定理三相似三角形的判定及性质1．相似三角形的判定2．相似三角形的性质四直角三角形的射影定理第二讲直线与圆的位置关系一圆周角定理二圆内接四边形的性质与判定定理三圆的切线的性质及判定定理四弦切角的性质五与圆有关的比例线段第三讲圆锥曲线性质的探讨一平行摄影二平面与圆柱面的截线三平面与圆锥面的截线选修4-2引言第一讲线性变换与二阶矩阵一线性变换与二阶矩阵（一）几类特殊线性变换及其二阶矩阵1.旋转变换2.反射变换3.伸缩变换4.投影变换5.切变变换（二）变换、矩阵的相等二二阶矩阵与平面向量的乘法（二）一些重要线性变换对单位正方形区域的作用第二讲变换的复合与二阶矩阵的乘法一复合变换与二阶矩阵的乘法二矩阵乘法的性质第三讲逆变换与逆矩阵一逆变换与逆矩阵1.逆变换与逆矩阵2.逆矩阵的性质二二阶行列式与逆矩阵三逆矩阵与二元一次方程组1.二元一次方程组的矩阵形式2.逆矩阵与二元一次方程组第四讲变换的不变量与矩阵的特征向量一变换的不变量——矩阵的特征向量1.特征值与特征向量2.特征值与特征向量的计算二特征向量的应用1.Ａa的简单表示2.特征向量在实际问题中的应用选修4-5第一章不等式的基本性质和证明的基本方法1．1 不等式的基本性质和一元二次不等式的解法1．2基本不等式1．3绝对值不等式的解法1．4绝对值的三角不等式1．5不等式证明的基本方法本章小结第二章柯西不等式与排序不等式及其应用2．1 柯西不等式2．2排序不等式2．3平均值不等式(选学)2．4最大值与最小值问题，优化的数学模型本章小结阅读与欣赏第三章数学归纳法与贝努利不等式3．1数学归纳法原理3．2用数学归纳法证明不等式，贝努利不等式本章小结阅读与欣赏附录部分中英文词汇对照表后记选修4-6引言第一讲整数的整除一整除1.整除的概念和性质2.带余除法3.素数及其判别法二最大公因数与最小公倍数1.最大公因数2.最小公倍数三算术基本定理第二讲同余与同余方程一同余1.同余的概念2.同余的性质二剩余类及其运算三费马小定理和欧拉定理四一次同余方程五拉格朗日插值法和孙子定理六弃九验算法第三讲一次不定方程一二元一次不定方程二二元一次不定方程的特解三多元一次不定方程第四讲数伦在密码中的应用一信息的加密与去密二大数分解和公开密钥学习总结报告附录一剩余系和欧拉函数附录二多项式的整除性选修4-7引言第一讲优选法一什么叫优选法二单峰函数三黄金分割法——0.618法1.黄金分割常数2.黄金分割法——0.618法阅读与思考黄金分割研究简史四分数法1.分数法阅读与思考斐波那契数列和黄金分割2.分数法的最优性五其他几种常用的优越法1.对分法2.盲人爬山法3.分批试验法4.多峰的情形六多因素方法1.纵横对折法和从好点出发法2.平行线法3.双因素盲人爬山法第二讲试验设计初步一正交试验设计法1.正交表2.正交试验设计3.试验结果的分析4.正交表的特性二正交试验的应用选修4-9引言第一讲风险与决策的基本概念一风险与决策的关系二风险与决策的基本概念1.风险（平均损失）2.平均收益3.损益矩阵4.风险型决策探究与发现风险相差不大时该如何决策第二讲决策树方法第三讲风险型决策的敏感性分析第四讲马尔可夫型决策简介一马尔可夫链简介1.马尔可夫性与马尔可夫链2.转移概率与转移概率矩阵二马尔可夫型决策简介三长期准则下的马尔可夫型决策理论1.马尔可夫链的平稳分布2.平稳分布与马尔可夫型决策的长期准则3.平稳准则的应用案例说明：A版适用于文件生使用，B版适用于理科生使用，B 版比A版略难。

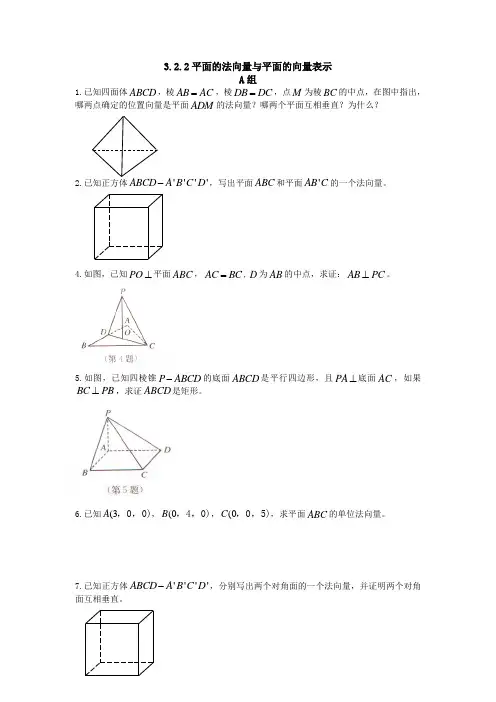
3.2.2平面的法向量与平面的向量表示
A 组
1.已知四面体ABCD ，棱AB AC =，棱DB DC =，点M 为棱BC 的中点，在图中指出，哪两点确定的位置向量是平面ADM 的法向量？哪两个平面互相垂直？为什么？
2.已知正方体''''ABCD A B C D -，写出平面ABC 和平面'AB C 的一个法向量。

4.如图，已知PO ⊥平面ABC ，AC BC =,D 为AB 的中点，求证：AB PC ⊥。

5.如图，已知四棱锥P ABCD -的底面ABCD 是平行四边形，且PA ⊥底面AC ，如果BC PB ⊥，求证ABCD 是矩形。

6.已知(3A ，0，0)，(0B ，4，0)，(0C ，0，5)，求平面ABC 的单位法向量。

7.已知正方体''''ABCD A B C D -，分别写出两个对角面的一个法向量，并证明两个对角面互相垂直。

8.已知四面体ABCD 的棱AB CD ⊥，AC BD ⊥，求证：AD BC ⊥。

B 组
9.直四棱柱1111ABCD A BC D -中，底面ABCD 是矩形，121 3.AB AD AA ===，， M 是BC 的中点.在1DD 上是否存在一点N ，使1MN DC ⊥？。

3.2.2 平面的法向量与平面的向量表示峡山中学 高二数学组 2010-12-23【课标点击】(一)学习目标：1、掌握平面的法向量；2、利用平面的法向量判定平面的位置关系；3、平面的向量表示；4、线面垂直的判定定理；5、三垂线定理.(二)教学重、难点：平面的向量表示、线面垂直的判定，面面垂直的判定【课前准备】（一）知识连接：1、 空间直线的向量参数方程：a t OA OP +=或OB t OA t OP +-=)1(2、 设P 为AB 之中点则)(21OB OA OP +=3、 直线1l 与2l 的方向向量为1v 和2v ，则2121////v v l l ⇔，212121v v v v l l ⋅⇔⊥⇔⊥=04、 两直线成的角，与两直线的方向向量成角的关系5、 p 与a ，b 共面（a ，b 不共线）⇔R y x ∈∃,使b y a x p +=6、 点A 、B 、C 不共线，则点A 、B 、C 、P 共面⇔∃x 、y R ∈使AC y AB x AP += （二）问题导引：如何证明线面平行、线面垂直、面面平行、面面垂直？【学习探究】（一）自学引导：自主学习课本102页至103页部分． 1、平面的法向量2、直线与平面垂直的判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面（用向量方法证明）3、平面的向量表示：4、设1n 、2n分别是平面α、β的法向量，那么：α//β或α与β重合⇔ 21//n n αβ⊥⇔21n n ⊥5、三垂线定理 在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直已知：,PO PA 分别是平面α的垂线和斜线，O A 是P A 在平面α内的射影，a α⊂，且a O A ⊥求证：a P A ⊥；证明：∵P O α⊥ ∴PO a ⊥，又∵,a OA PO OA O ⊥=∴a ⊥平面P O A ，∴a P A ⊥． 说明：（1）定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系；（2）推理模式：,,PO O PA A a PA a a O A αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭6条斜线的射影垂直证明思路： ,,PO O PA A a AO a a AP αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭．（二）思考与讨论：⑴三垂线指： （PA ，PO ，AO 都垂直α内的直线a ）2）其实质是： （ 斜线和平面内一条直线垂直的判定和性质定理）注意：要考虑a 的位置，并注意两定理交替使用（三）典型例题:例1．在正方体111ABCD A B C D -中，求证：1D B是平面1AC D 的法向量．例2：已知正方体''''ABC D A B C D -.求证：平面''//A B D 平面'B D C .例3.如图，底面A B C D 是正方形，SA ⊥底面A B C D ，且SA AB =，E 是S C 中点. 求证：平面BD E ⊥平面A B C D .说明：一．证明垂直关系，可通过向量的数量积等于0来实现；二．要善于转化，即挖掘已知的垂直关系，将未知向已知转化（四）变式拓展：已知正方体1111ABC D A B C D -中，,E F 分别为1,BB C D 的中点， 求证：1D F ⊥平面A D E 。

3.2.2 利用向量解决平行、垂直问题1．用向量方法证明空间中的平行关系(1)证明线线平行设直线l，m的方向向量分别是a＝(a1，b1，c1)，b＝(a2，b2，c2)，则l∥m⇔□01a∥b⇔□02 a＝λb⇔□03a1＝λa2，b1＝λb2，c1＝λc2(λ∈R)．(2)证明线面平行设直线l的方向向量为a＝(a1，b1，c1)，平面α的法向量为u＝(a2，b2，c2)，则l∥α⇔□04a⊥u⇔□05a·u＝0⇔□06a1a2＋b1b2＋c1c2＝0.(3)证明面面平行①设平面α，β的法向量分别为u＝(a1，b1，c1)，v＝(a2，b2，c2)，则α∥β⇔□07u∥v⇔u＝λv⇔□08a1＝λa2，b1＝λb2，c1＝λc2(λ∈R)．②由面面平行的判定定理，要证明面面平行，只要转化为相应的线面平行、线线平行即可．2．用向量方法证明空间中的垂直关系(1)证明线线垂直设直线l1的方向向量u1＝(a1，b1，c1)，直线l2的方向向量u2＝(a2，b2，c2)，则l1⊥l2⇔□09u1⊥u2⇔□10u1·u2＝0⇔□11a1a2＋b1b2＋c1c2＝0.(2)证明线面垂直设直线l的方向向量是u＝(a1，b1，c1)，平面α的法向量v＝(a2，b2，c2)，则l⊥α⇔□12 u∥v⇔□13u＝λv(λ∈R)⇔□14a1＝λa2，b1＝λb2，c1＝λc2(λ∈R)．(3)证明面面垂直若平面α的法向量u＝(a1，b1，c1)，平面β的法向量v＝(a2，b2，c2)，则α⊥β⇔□15u ⊥v⇔□16u·v＝0⇔□17a1a2＋b1b2＋c1c2＝0.1．判一判(正确的打“√”，错误的打“×”)(1)若两直线方向向量的数量积为0，则这两条直线一定垂直相交．( )(2)若一直线与平面垂直，则该直线的方向向量与平面内的所有直线的方向向量的数量积为0.( )(3)两个平面垂直，则其中一平面内的直线的方向向量与另一平面内的直线的方向向量垂直．( )答案 (1)× (2)√ (3)×2．做一做(请把正确的答案写在横线上)(1)若直线l 1的方向向量为u 1＝(1,3,2)，直线l 2上有两点A (1,0,1)，B (2，－1,2)，则两直线的位置关系是________．(2)若直线l 的方向向量为a ＝(1,0,2)，平面α的法向量为n ＝(－2,0，－4)，则直线l 与平面α的位置关系为________．(3)已知两平面α，β的法向量分别为u 1＝(1,0,1)，u 2＝(0,2,0)，则平面α，β的位置关系为________．(4)若平面α，β的法向量分别为(－1,2,4)，(x ，－1，－2)，并且α⊥β，则x 的值为________．答案 (1)垂直 (2)垂直 (3)垂直 (4)－10探究1 利用空间向量解决平行问题例1 已知正方体ABCD －A 1B 1C 1D 1的棱长为2，E ，F 分别是BB 1，DD 1的中点，求证： (1)FC 1∥平面ADE ； (2)平面ADE ∥平面B 1C 1F .[证明] (1)如图所示，建立空间直角坐标系Dxyz ，则有D (0,0,0)，A (2,0,0)，C 1(0,2,2)，E (2,2,1)，F (0，0,1)，B 1(2,2,2)， 所以FC 1→＝(0,2,1)，DA →＝(2,0,0)，AE →＝(0,2,1)．设n 1＝(x 1，y 1，z 1)是平面ADE 的法向量，则n 1⊥DA →，n 1⊥AE →， 即⎩⎪⎨⎪⎧n 1·DA →＝2x 1＝0，n 1·AE →＝2y 1＋z 1＝0，得⎩⎪⎨⎪⎧x 1＝0，z 1＝－2y 1，令z 1＝2，则y 1＝－1，所以n 1＝(0，－1,2)． 因为FC 1→·n 1＝－2＋2＝0，所以FC 1→⊥n 1.又因为FC 1⊄平面ADE ，所以FC 1∥平面ADE . (2)因为C 1B 1→＝(2,0,0)，设n 2＝(x 2，y 2，z 2)是平面B 1C 1F 的一个法向量． 由n 2⊥FC 1→，n 2⊥C 1B 1→，得 ⎩⎪⎨⎪⎧n 2·FC 1→＝2y 2＋z 2＝0，n 2·C 1B 1→＝2x 2＝0，得⎩⎪⎨⎪⎧x 2＝0，z 2＝－2y 2.令z 2＝2，得y 2＝－1，所以n 2＝(0，－1,2)， 因为n 1＝n 2，所以平面ADE ∥平面B 1C 1F . 拓展提升利用向量法证明平行问题的两种途径(1)利用三角形法则和平面向量基本定理实现向量间的相互转化，得到向量的共线关系； (2)通过建立空间直角坐标系，借助直线的方向向量和平面的法向量进行平行关系的证明．【跟踪训练1】 在长方体ABCD －A 1B 1C 1D 1中，AB ＝4，AD ＝3，AA 1＝2，P ，Q ，R ，S 分别是AA 1，D 1C 1，AB ，CC 1的中点．求证：PQ ∥RS .证明 证法一：以D 为原点，DA ，DC ，DD 1所在直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系Dxyz .则P (3,0,1)，Q (0,2,2)，R (3,2,0)，S (0,4,1)， PQ →＝(－3,2,1)，RS →＝(－3,2,1)，∴PQ →＝RS →，∴PQ →∥RS →，即PQ ∥RS . 证法二：RS →＝RC →＋CS →＝12DC →－DA →＋12DD 1→，PQ →＝PA 1→＋A 1Q →＝12DD 1→＋12DC →－DA →，∴RS →＝PQ →，∴RS →∥PQ →，即RS ∥PQ . 探究2 利用空间向量解决垂直问题例2 如图，在四棱锥E －ABCD 中，AB ⊥平面BCE ，CD ⊥平面BCE ，AB ＝BC ＝CE ＝2CD ＝2，∠BCE ＝120°.求证：平面ADE ⊥平面ABE .[证明] 取BE 的中点O ，连接OC ，则OC ⊥EB ， 又AB ⊥平面BCE .∴以O 为原点建立空间直角坐标系Oxyz .如图所示．则由已知条件有C (1，0,0)，B (0，3，0)，E (0，－3，0)，D (1,0,1)，A (0，3，2)． 设平面ADE 的法向量为n ＝(a ，b ，c )，则n ·EA →＝(a ，b ，c )·(0,23，2)＝23b ＋2c ＝0，n ·DA →＝(a ，b ，c )·(－1，3，1)＝－a ＋3b ＋c ＝0.令b ＝1，则a ＝0，c ＝－3， ∴n ＝(0,1，－3)．∵AB ⊥平面BCE ，∴AB ⊥OC ，又OC ⊥EB ，且EB ∩AB ＝B ，∴OC ⊥平面ABE ， ∴平面ABE 的法向量可取为m ＝(1,0,0)． ∵n ·m ＝(0,1，－3)·(1,0,0)＝0， ∴n ⊥m ，∴平面ADE ⊥平面ABE . 拓展提升利用向量法证明几何中的垂直问题的两条途径(1)利用三角形法则和平面向量基本定理实现向量间的相互转化，得到向量的垂直关系． (2)通过建立空间直角坐标系，借助直线的方向向量和平面的法向量进行证明．证明线面垂直时，只需直线的方向向量与平面的法向量平行或直线的方向向量与平面内两相交的直线的方向向量垂直．在判定两个平面垂直时，只需求出这两个平面的法向量，再看它们的数量积是否为0.【跟踪训练2】 如右图所示，在正方体ABCD －A 1B 1C 1D 1中，E ，F 分别是BB 1，D 1B 1的中点．求证：EF ⊥平面B 1AC .证明 证法一：设AB →＝a ，AD →＝c ，AA 1→＝b ，则EF →＝EB 1→＋B 1F →＝12(BB 1→＋B 1D 1→)＝12(AA 1→＋BD →)＝12(AA 1→＋AD →－AB →)＝12(－a ＋b ＋c )，∵AB 1→＝AB →＋AA 1→＝a ＋b .∴EF →·AB 1→＝12(－a ＋b ＋c )·(a ＋b )＝12(b 2－a 2＋c ·a ＋c ·b ) ＝12(|b |2－|a |2＋0＋0)＝0. ∴EF →⊥AB 1→，即EF ⊥AB 1，同理，EF ⊥B 1C . 又AB 1∩B 1C ＝B 1， ∴EF ⊥平面B 1AC .证法二：设正方体的棱长为2，以DA ，DC ，DD 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的直角坐标系，则A (2,0,0)，C (0,2,0)，B 1(2,2,2)，E (2,2,1)，F (1,1,2)．∴EF →＝(1,1,2)－(2,2,1) ＝(－1，－1,1)．AB 1→＝(2,2,2)－(2,0,0)＝(0,2,2)，AC →＝(0,2,0)－(2,0,0)＝(－2,2,0)，∴EF →·AB 1→＝(－1，－1,1)·(0,2,2)＝(－1)×0＋(－1)×2＋1×2＝0.EF →·AC →＝(－1，－1,1)·(－2,2,0)＝2－2＋0＝0， ∴EF →⊥AB 1→，EF →⊥AC →， ∴EF ⊥AB 1，EF ⊥AC . 又AB 1∩AC ＝A ， ∴EF ⊥平面B 1AC .证法三：同法二得AB 1→＝(0,2,2)，AC →＝(－2,2,0)， EF →＝(－1，－1,1)．设面B 1AC 的法向量n ＝(x ，y ，z )， 则AB →1·n ＝0，AC →·n ＝0，即⎩⎪⎨⎪⎧2y ＋2z ＝0，－2x ＋2y ＝0，取x ＝1，则y ＝1，z ＝－1，∴n ＝(1,1，－1)，∴EF →＝－n ，∴EF →∥n ，∴EF ⊥平面B 1AC . 探究3 与平行、垂直有关的探索性问题例3 如图，在三棱锥P －ABC 中，AB ＝AC ，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上，已知BC ＝8，PO ＝4，AO ＝3，OD ＝2.(1)证明：AP ⊥BC ；(2)在线段AP 上是否存在点M ，使得平面AMC ⊥平面BMC ？若存在，求出AM 的长；若不存在，请说明理由．[解] (1)证明：如图，以O 为原点，以射线OD 为y 轴的正半轴，射线OP 为z 轴的正半轴，建立空间直角坐标系Oxyz .则O (0,0,0)，A (0，－3,0)，B (4,2,0)，C (－4,2,0)，P (0,0,4)， AP →＝(0,3,4)，BC →＝(－8,0,0)，由此可得AP →·BC →＝0，所以AP →⊥BC →，即AP ⊥BC .(2)假设存在满足题意的M ，设PM →＝λPA →，λ≠1，则PM →＝λ(0，－3，－4)．BM →＝BP →＋PM →＝BP →＋λPA →＝(－4，－2,4)＋λ(0，－3，－4)＝(－4，－2－3λ，4－4λ)，AC →＝(－4,5,0)．设平面BMC 的法向量n 1＝(x 1，y 1，z 1)， 平面APC 的法向量n 2＝(x 2，y 2，z 2)． 由⎩⎪⎨⎪⎧BM →·n 1＝0，BC →·n 1＝0，得⎩⎪⎨⎪⎧－4x 1－(2＋3λ)y 1＋(4－4λ)z 1＝0，－8x 1＝0，即⎩⎪⎨⎪⎧x 1＝0，z 1＝2＋3λ4－4λy 1，可取n 1＝⎝ ⎛⎭⎪⎫0，1，2＋3λ4－4λ.由⎩⎪⎨⎪⎧AP →·n 2＝0，AC →·n 2＝0，即⎩⎪⎨⎪⎧3y 2＋4z 2＝0，－4x 2＋5y 2＝0，得⎩⎪⎨⎪⎧x 2＝54y 2，z 2＝－34y 2，可取n 2＝(5,4，－3)，由n 1·n 2＝0，得4－3×2＋3λ4－4λ＝0，解得λ＝25，故PM →＝⎝ ⎛⎭⎪⎫0，－65，－85，AM →＝AP →＋PM →＝⎝ ⎛⎭⎪⎫0，95，125，所以AM ＝3.综上所述，存在点M 符合题意，AM ＝3. 拓展提升利用向量解决探索性问题的方法对于探索性问题，一般先假设存在，利用空间坐标系，结合已知条件，转化为代数方程是否有解的问题，若有解满足题意则存在，若没有满足题意的解则不存在．【跟踪训练3】 如图，直三棱柱ABC －A 1B 1C 1中，AC ＝3，BC ＝4，AB ＝5，AA 1＝4.(1)求证：BC 1⊥平面AB 1C ；(2)在AB 上是否存在点D ，使得AC 1∥平面CDB 1.解 (1)证明：由已知AC ＝3，BC ＝4，AB ＝5，因而△ABC 是∠ACB 为直角的直角三角形，由三棱柱是直三棱柱，则CC 1⊥平面ABC ，以CA ，CB ，CC 1分别为x ，y ，z 轴建立空间直角坐标系，从而CA →＝(3,0,0)，BC 1→＝(0，－4,4)，则BC 1→·CA →＝(0，－4,4)·(3,0,0)＝0，则BC 1→⊥AC →，所以BC 1⊥AC .又四边形BCC 1B 1为正方形，因而BC 1⊥B 1C .又∵B 1C ∩AC ＝C ，∴BC 1⊥平面AB 1C .(2)假设存在点D (x ，y,0)，使得AC 1∥平面CDB 1，CD →＝(x ，y,0)，CB 1→＝(0,4,4)， 设平面CDB 1的法向量m ＝(a ，b ，c )，则⎩⎪⎨⎪⎧m ·CD →＝0，m ·CB 1→＝0，即⎩⎪⎨⎪⎧xa ＋yb ＝0，4b ＋4c ＝0.令b ＝－x ，则c ＝x ，a ＝y ，所以m ＝(y ，－x ，x )，而AC 1→＝(－3,0,4)，则AC 1→·m ＝0，得－3y ＋4x ＝0.① 由D 在AB 上，A (3,0,0)，B (0,4,0)得x －3－3＝y4，即得4x ＋3y ＝12，② 联立①②可得x ＝32，y ＝2，∴D ⎝ ⎛⎭⎪⎫32，2，0，即D 为AB 的中点． 综上，在AB 上存在点D ，使得AC 1∥平面CDB 1，点D 为AB 的中点．1.利用向量证明线线平行的两种思路一是建立空间直角坐标系，通过坐标运算，利用向量平行的坐标表示证明；二是用基底思路，通过向量的线性运算，利用共线向量定理证明.2.向量法证明线线垂直的方法用向量法证明空间中两条直线相互垂直，其主要思路是证明两条直线的方向向量相互垂直．具体方法为：(1)坐标法：根据图形的特征，建立适当的空间直角坐标系，准确地写出相关点的坐标，表示出两条直线的方向向量，证明其数量积为0.(2)基向量法：利用向量的加减运算，结合图形，将要证明的两条直线的方向向量用基向量表示出来．利用数量积运算说明两向量的数量积为0.3.向量法证明线面垂直的方法(1)向量基底法，具体步骤如下：①设出基向量，用基向量表示直线的方向向量；②找出平面内两条相交直线的方向向量并分别用基向量表示；③分别计算直线的方向向量与平面内两条相交直线的方向向量的数量积.(2)坐标法，具体方法如下：方法一：①建立空间直角坐标系；②将直线的方向向量用坐标表示；③将平面内任意两条相交直线的方向向量用坐标表示；④分别计算直线的方向向量与平面内两条相交直线的方向向量的数量积.方法二：①建立空间直角坐标系；②将直线的方向向量用坐标表示；③求平面的法向量；④说明平面的法向量与直线的方向向量平行.4.证明面面垂直的两种思路一是证明其中一个平面过另一个平面的垂线，即转化为线面垂直；二是证明两平面的法向量垂直.1．已知线段AB的两端点坐标为A(9，－3,4)，B(9,2,1)，则线段AB与坐标平面( ) A．xOy平行B．xOz平行C．yOz平行D．yOz相交答案 C解析 因为AB →＝(9,2,1)－(9，－3,4)＝(0,5，－3)，所以AB ∥平面yOz .2．若两个不同平面α，β的法向量分别为u ＝(1,2，－1)，v ＝(－3，－6,3)，则( ) A ．α∥β B ．α⊥βC ．α，β相交但不垂直D ．以上均不正确 答案 A解析 ∵v ＝－3u ，∴α∥β.3．已知直线l 与平面α垂直，直线l 的一个方向向量为u ＝(1，－3，z )，向量v ＝(3，－2,1)与平面α平行，则z 等于( )A ．3B ．6C ．－9D ．9 答案 C解析 ∵l ⊥α，v 与平面α平行，∴u ⊥v ，即u ·v ＝0，∴1×3＋3×2＋z ×1＝0，∴z ＝－9.4．在三棱锥P －ABC 中，CP ，CA ，CB 两两垂直，AC ＝CB ＝1，PC ＝2，在如图所示的空间直角坐标系中，下列向量中是平面PAB 的法向量的是( )A.⎝⎛⎭⎪⎫1，1，12 B ．(1，2，1) C ．(1,1,1) D ．(2，－2,1) 答案 A解析 PA →＝(1,0，－2)，AB →＝(－1,1,0)，设平面PAB 的一个法向量为n ＝(x ，y,1)，则x －2＝0，即x ＝2；－x ＋y ＝0，即y ＝x ＝2.所以n ＝(2,2,1)．因为⎝⎛⎭⎪⎫1，1，12＝12n ，所以A正确．5．在棱长为1的正方体ABCD －A 1B 1C 1D 1中，M 为棱BB 1的中点，在棱DD 1上是否存在点P ，使MD ⊥平面PAC?解 如图，建立空间直角坐标系，则A (1,0,0)，C (0,1,0)，D (0,0,0)，M ⎝⎛⎭⎪⎫1，1，12.假设存在P (0,0，x )满足条件，则PA →＝(1,0，－x )，AC →＝(－1,1,0)．设平面PAC 的法向量为n ＝(x 1，y 1，z 1)，则由⎩⎪⎨⎪⎧ PA →·n ＝0，AC →·n ＝0，得⎩⎪⎨⎪⎧ x 1－xz 1＝0，－x 1＋y 1＝0.令x 1＝1得y 1＝1，z 1＝1x ，即n ＝⎝ ⎛⎭⎪⎫1，1，1x ， 由题意MD →∥n ，由MD →＝⎝⎛⎭⎪⎫－1，－1，－12，得x ＝2， ∵正方体棱长为1，且2>1，∴棱DD 1上不存在点P ，使MD ⊥平面PAC .。

3.2.2平面的法向量与平面的向量表示班级___姓名：__________时间2012.2.10 一、【教材知识梳理】1.已知平面α，如果向量n 的基线与平面α垂直，则向量n叫做____________________。

2.平面α的一个法向量垂直于与平面α共面的所有向量，同时，一个平面的所有法向量____________。

3.如果一条直线和平面内的两条___________直线垂直，那么这条直线_______于这个平面。

4.设12n n 、分别是平面αβ、的法向量，则容易得到：α∥β或（αβ、重合）⇔_________，12n n αβ⊥⇔⊥⇔_______________。

5.已知平面α和一点A ，过点A 作α的垂线l 与α相交于点'A ，则'A 就是点A 在平面α内的________，简称_________________。

6.如果一条直线AB 和平面α相交于点B ，但不和α垂直，那么直线AB 叫做这个平面的____________，斜线和平面的交点B 叫做____________，斜线上一点A 与斜足B 之间的线段叫做_____________。

7.如果在平面内的一条直线与平面的一条斜线在这个平面的____________重直，则它也和这条_________垂直。

8.如果________________的一条直线和这个平面的一条斜线垂直，则它也和这条斜线在平面内的______垂直。

二、【课前检测】1.若平面αβ、的法向量分别为1n =（1，2，-2），2n =（-3，-6，6），则（ ） A.α∥β B.αβ⊥ C.αβ，相交但不垂直 D.以上说法都不对2.已知==AB AC（2，2，1），（4，5，3），则平面ABC 的一个单位法向量为（ ）A.122333（-，-，-） B.122333（-，，-） C.122333（-，，） D. 122333（，，）3.设平面α的法向量为（1，2，-2），平面β的法向量为k （-2，-4，），若α∥β，则k =__________；若αβ⊥，则k =________________。

3.2.2平面的法向量与平面的向量表示一、选择题1．下列命题中正确的是( )A ．如果一条直线与平面的一条斜线在这个平面内的射影垂直，则它也和这条斜线垂直B ．如果一条直线与平面的一条斜线垂直，则它与斜线在平面上的射影垂直C ．如果一向量和斜线在平面内的射影垂直，则它垂直于这条斜线D ．如果一非零向量和一平面平行，且和一条斜线垂直，则它垂直于斜线在平面内的射影[答案] D[解析] 由三垂线定理知D 成立．2．在正方体ABCD —A 1B 1C 1D 1中，平面ACB 1的一个法向量为( )A.BD 1→B.DB →C.BA 1→D.BB 1→ [答案] A3．点A (a,0,0)，B (0，b,0)，C (0,0，c )，则平面ABC 的一个法向量为( )A ．(bc ，ac ，ab )B ．(ac ，ab ，bc )C ．(bc ，ab ，ac )D ．(ab ，ac ，bc ) [答案] A[解析] 设法向量为n ＝(x ，y ，z )，则AB ·n ＝0，AC →·n ＝0，则⎩⎪⎨⎪⎧－ax ＋by ＝0－ax ＋cz ＝0∴n ＝(bc ，ac ，ab )． 故选A. 4．在正方体ABCD －A 1B 1C 1D 1中，若E 为A 1C 1的中点，则直线CE 垂直于( ) A ．ACB ．BDC ．A 1DD ．A 1A[答案] B[解析] 直线CE 在平面AC 内的射影为AC ，又AC ⊥BD ，∴BD ⊥CE ，故选B.5．正方体AC 1中，E ，F 分别是AB ，CD 的中点，则下列直线中不互相垂直的是( )A ．B 1C 与C 1D 1B ．D 1B 与B 1C C ．D 1B 与EFD ．A 1B 与B 1C 1 [答案] C[解析]D1B与EF所成角等于∠D1BC，其余弦值为33，故选C.6．若平面α、β的法向量分别为u＝(－2,3，－5)，v＝(3，－1,4)，则()A．α∥βB．α⊥βC．α、β相交但不垂直D．以上均不正确[答案] C[解析]∵u＝(－2,3，－5)，v＝(3，－1,4)，∴u与v不平行且u与v不垂直，故选C.7．平面α的一个法向量为v1＝(1,2,1)，平面β的一个法向量v2＝－(2,4,2)，则平面α与平面β()A．平行B．垂直C．相交D．不能确定[答案] A[解析]由v1∥v2故可判定α∥β.8．设平面α的法向量为(1,2，－2)，平面β的法向量(－2，－4，k)，若α∥β，则k＝() A．2B．－4C．4D．－2[答案] C[解析]∵α∥β，∴1－2＝2－4＝－2k，∴k＝4，故选C.9．若直线l的方向向量为a＝(－1,0，－2)，平面α的法向量为u＝(4,0,8)，则() A．l∥αB．l⊥αC．l⊂αD．l与α斜交[答案] B[解析]∵u＝－4a，∴u∥a，∴a⊥α，∴l⊥α.故选B.10．在正方体ABCD—A1B1C1D1中，E、F分别是BB1、CD的中点，则()A．面AED∥面A1FD1B．面AED⊥面A1FD1C．面AED与面A1FD相交但不垂直D．以上都不对[答案] B[解析] 以D 为原点，DA →、DC →，DD 1→分别为x ，y ，z 建立空间直角坐标系求面AED 的法向量n 1与面A 1FD 1的法向量n 2.∵n 1·n 2＝0，∴n 1⊥n 2，∴平面AED ⊥平面A 1FD 1.二、填空题11．若直线l 与β的法向量分别是a ＝(1,0，－2)，b ＝(－1，0,2)，则直线l 与β的位置关系是________．[答案] l ⊥β[解析] ∵a ∥b ，∴l ⊥β.12．已知l ∥α，且l 的方向向量为(2，m,1)，平面α的法向量为⎝⎛⎭⎫1，12，2，则m ＝________.[答案] －8[解析] 设a ＝(2，m,1)，b ＝(1，12，2)． ∵l ∥α，∴a ⊥b ，∴2＋12m ＋2＝0，∴m ＝－8. 13．已知正四棱锥(如图所示)，在向量PA →－PB →＋PC →－PD →，PA→＋PC →，PB →＋PD →，PA →＋PB →＋PC →＋PD →中，不能作为底面ABCD 的法向量的向量是________．[答案] PA →－PB →＋PC →－PD →[解析] ∵PA →－PB →＋PC →－PD →＝BA →＋DC →＝0，不能作为这个平面的法向量，对其它三个化简后可知均与PO →共线．而PO ⊥平面ABCD ，它们可作为这个平面的法向量．14．如图所示，已知矩形ABCD ，AB ＝1，BC ＝a ，P A ⊥平面ABCD ，若在BC 上只有一个点Q 满足PQ ⊥QD ，则a 的值等于________．[答案] 2[解析] 以A 为原点，建立如图所示坐标系，则A (0,0,0)，B (1,0,0)，D (0，a,0)，C (1，a,0)，设Q (1，x,0)，P (0,0，z )，PQ →＝(1，x ，－z )，QD→＝(－1，a －x,0)．由PQ →·QD →＝0，得－1＋x (a －x )＝0，即x 2－ax ＋1＝0.当Δ＝a 2－4＝0，即a ＝2时，Q 只有一个．三、解答题15．已知△ABC 的三个顶点坐标分别为A (0,0,2)，B (4,2,0)，C (2,4,0)，求平面ABC 的单位法向量．[解析] AB →＝(4,2，－2)，AC →＝(2,4，－2)设n ＝(x ，y ，z )是平面ABC 的单位法向量，则有⎩⎪⎨⎪⎧ |n |2＝1，n ·AB →＝0，n ·AC →＝0，⇒⎩⎪⎨⎪⎧ x 2＋y 2＋z 2＝1，2x ＋y －z ＝0，x ＋2y －z ＝0. 取z >0，得x ＝y ＝111，z ＝311 . ∴n ＝111(1,1,3)．16．如图所示，M 、N 、P 分别是正方体ABCD —A 1B 1C 1D 1中的棱CC 1、BC 、CD 的中点．求证：A 1P ⊥平面DMN .[证明] 建立如图所示的空间直角坐标系，设正方体棱长为2，则D (0,0,0)，A 1(2,0,2)，P (0,1,0)，M (0,2,1)，N (1,2,0)．∴向量A 1P →＝(0,1,0)－(2,0,2)＝(－2,1，－2)，DM →＝(0,2,1)－(0,0,0)＝(0,2,1)，DN →＝(1,2,0)．∴A 1P →·DM →＝(－2,1，－2)·(0,2,1)＝(－2)×0＋1×2＋(－2)×1＝0.A 1P →·DN →＝(－2,1，－2)·(1,2,0)＝(－2)×1＋1×2＋(－2)×0＝0.∴A 1P →⊥DM →，A 1P →⊥DN →，即A 1P ⊥DM ，A 1P ⊥DN ，又DM ∩DN ＝D ，∴A 1P ⊥平面DMN .17．棱长为a 的正方体ABCD —A 1B 1C 1D 1中，在棱DD 1上是否存在点P 使B 1D ⊥面P AC?[解析] 以D 为原点建立如图所示的坐标系，设存在点P (0,0，z )，AP →＝(－a,0，z )，AC →＝(－a ，a,0)，DB 1→＝(a ，a ，a )，∴B 1D ⊥面PAC ，∴DB 1→·AP →＝0，DB 1→·AC →＝0.∴－a 2＋az ＝0.∴z ＝a ，即点P 与D 1重合．∴点P 与D 1重合时，DB 1⊥面P AC .18．如图所示，ABCD 为矩形，PA ⊥平面ABCD ，PA ＝AD ，M 、N 、Q 分别是PC 、AB 、CD 的中点，(1)求证：MN ∥PAD ；(2)求证：平面QMN ∥平面PAD ；(3)求证：MN ⊥平面PCD .[解析] (1)如图以A 为原点，以AB ，AD ，AP 所在直线为坐标轴建立空间直角坐标系，设B (b,0,0)，D (0，d,0)，P (0,0，d )，则C (b ，d,0)∵M ，N ，Q 分别是PC ，AB ，CD 的中点，∴M ⎝⎛⎭⎫b 2，d 2，d 2，N ⎝⎛⎭⎫b 2，0，0，Q ⎝⎛⎭⎫b 2，d ，0 ∴MN →＝⎝⎛⎭⎫0，－d 2，－d 2， ∵面PAD 的一个法向量为m ＝(1,0,0)∴MN →·m ＝0，即MN →⊥m ，∴MN 不在面P AD 内，∴MN ∥面PAD ，(2)QN →＝(0，－d,0)，QN →⊥m ，又QN 不在面P AD 内，又QN ∥面PAD .又∵MN ∩QN ＝N ，∴面MNQ ∥平面P AD .(3)PD →＝(0，d ，－d )，DC →＝(b,0,0)， ∴MN →·PD →＝⎝⎛⎭⎫－d 2d ＋⎝⎛⎭⎫－d 2(－d )＝0， MN →·DC →＝0，∴MN →⊥PD →，MN →⊥DC ，又PD ∩DC ＝D ， ∴MN →⊥平面PCD .。

3.2.2 平面的法向量与平面的向量表示1．理解平面的法向量的概念， 会求平面的法向量．(重点) 2．会用平面的法向量证明平面与平面平行、垂直．(重点)3．理解并会应用三垂线定理及其逆定理，证明有关垂直问题．(难点)[基础·初探]教材整理1 平面的法向量与向量表示 阅读教材P 102～P 103“例1”，完成下列问题． 1．平面的法向量已知平面α，如果向量n 的基线与平面α垂直，则向量n 叫做平面α的法向量或说向量n 与平面α正交．2．平面的向量表示设A 是空间任一点，n 为空间内任一非零向量，适合条件AM →·n ＝0的点M 的集合构成的图形是过空间内一点A 并且与n 垂直的平面．这个式子称为一个平面的向量表示式．3．两平面平行、垂直的判定设n 1，n 2分别是平面α，β的法向量，则 (1)α∥β或α与β重合⇔n 1∥n 2； (2)α⊥β⇔n 1⊥n 2⇔n 1·n 2＝0.1．若直线l 的方向向量a ＝(1,0,2)，平面α的法向量为n ＝(－2,0，－4)，则( ) A ．l ∥α B ．l ⊥α C ．l ⊂αD ．l 与α斜交【解析】 ∵n ＝(－2,0，－4)＝－2(1,0,2)＝－2a ， ∴n ∥a ，∴l ⊥α. 【答案】 B2．若平面α，β的法向量分别为a ＝(2，－1,0)，b ＝(－1，－2,0)，则α与β的位置关系是( )A ．平行B ．垂直C．相交但不垂直D．无法确定【解析】∵a·b＝－2＋2＋0＝0，∴a⊥b，∴α⊥β.【答案】 B教材整理2 三垂线定理及其逆定理阅读教材P104第5行～P105第2行内容，完成下列问题．1．正射影已知平面α和一点A，过点A作α的垂线l与α相交于点A′，则A′就是点A在平面α内的正射影，简称射影．2．三垂线定理如果在平面内的一条直线与平面的一条斜线在这个平面内的射线垂直，则它也和这条斜线垂直．3．三垂线定理的逆定理如果平面内的一条直线和这个平面的一条斜线垂直，则它也和这条斜线在平面内的射影垂直．判断(正确的打“√”，错误的打“×”)(1)若a是平面α的一条斜线，直线b垂直于a在α内的射影，则a⊥b.( )(2)若a是平面α的斜线，平面β内的直线b垂直于a在平面α内的射影，则a⊥b.( )(3)若a是平面α的斜线，直线b⊂α，且b垂直于a在另一个平面β内的射影，则a ⊥b.( )(4)若a是平面α的斜线，b∥α，直线b垂直于a在平面α内的射影，则a⊥b.( )【答案】(1)×(2)×(3)×(4)√[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1：________________________________________________________解惑：________________________________________________________疑问2：________________________________________________________解惑：________________________________________________________疑问3：________________________________________________________解惑：________________________________________________________[小组合作型]利用平面法向量证明平行关系已知正方体ABCD ­A 1B 1C 1D 1的棱长为2，E ，F 分别是BB 1，DD 1的中点，求证： (1)FC 1∥平面ADE ； (2)平面ADE ∥平面B 1C 1F .【精彩点拨】 建立空间直角坐标系，利用平面的法向量求解．【自主解答】 (1)建立如图所示空间直角坐标系Dxyz ，则有D (0,0,0)，A (2,0,0)，C (0,2,0)，C 1(0,2,2)，E (2,2,1)，F (0,0,1)，B 1(2,2,2)，所以FC 1→＝(0,2,1)，DA →＝(2,0,0)，AE →＝(0,2,1)．设n 1＝(x 1，y 1，z 1)是平面ADE 的法向量，则n 1⊥DA →，n 1⊥AE →， 即⎩⎪⎨⎪⎧n 1·DA →＝2x 1＝0，n 1·AE →＝2y 1＋z 1＝0，得⎩⎪⎨⎪⎧x 1＝0，z 1＝－2y 1.令z 1＝2，则y 1＝－1， 所以n 1＝(0，－1,2)． 因为FC 1→·n 1＝－2＋2＝0， 所以FC 1→⊥n 1.又因为FC 1⊄平面ADE ， 所以FC 1∥平面ADE .(2)∵C 1B 1→＝(2,0,0)，设n 2＝(x 2，y 2，z 2)是平面B 1C 1F 的法向量．由n 2⊥FC 1→，n 2⊥C 1B 1→，得⎩⎪⎨⎪⎧n 2·FC 1→＝2y 2＋z 2＝0，n 2·C 1B 1→＝2x 2＝0，得⎩⎪⎨⎪⎧x 2＝0，z 2＝－2y 2.令z 2＝2，得y 2＝－1，所以n 2＝(0，－1,2)， 因为n 1＝n 2，所以平面ADE ∥平面B 1C 1F .用向量方法证明空间平行关系的方法线线 平行设直线l 1，l 2的方向向量分别是a ，b ，则要证明l 1∥l 2，只需证明a ∥b ，即a ＝k b (k ∈R )．线面平行(1)设直线l 的方向向量是a ，平面α的法向量是u ，则要证明l ∥α，只需证明a ⊥u ，即a ·u ＝0.(2)根据线面平行判定定理在平面内找一个向量与已知直线的方向向量是共线向量即可．(3)证明一条直线l 与一个平面α平行，只需证明l 的方向向量能用平面α内两个不共线向量线性表示即可．面面 平行 (1)转化为相应的线线平行或线面平行．(2)求出平面α，β的法向量u ，v ，证明u ∥v 即可说明α∥β.[再练一题]1．在正方体ABCD ­A 1B 1C 1D 1中，E ，F ，G ，H ，M ，N 分别是正方体六个表面的中心，证明：平面EFG ∥平面HMN .【证明】 如图所示，建立空间直角坐标系，不妨设正方体的棱长为2，则E (1,1,0)，F (1,0,1)，G (2,1,1)，H (1,1,2)，M (1,2,1)，N (0,1,1)．∴EF →＝(0，－1,1)， EG →＝(1,0,1)， HM →＝(0,1，－1)， HN →＝(－1,0，－1)．设m ＝(x 1，y 1，z 1)，n ＝(x 2，y 2，z 2)分别是平面EFG 和HMN 的法向量， 由⎩⎪⎨⎪⎧ m ·EF →＝0，m ·EG →＝0，得⎩⎪⎨⎪⎧－y 1＋z 1＝0，x 1＋z 1＝0，令x 1＝1，得m ＝(1，－1，－1)． 由⎩⎪⎨⎪⎧n ·HM →＝0，n ·HN →＝0，得⎩⎪⎨⎪⎧y 2－z 2＝0，－x 2－z 2＝0.令x 2＝1，得n ＝(1，－1，－1)．于是有m ＝n ，即m ∥n ，故平面EFG ∥平面HMN .利用向量证明线面垂直如图3­2­14所示，在正方体ABCD ­A 1B 1C 1D 1中，E ，F 分别是B 1B ，DC 的中点，求证：AE ⊥平面A 1D 1F .图3­2­14【精彩点拨】 建立空间直角坐标系，得到有关向量的坐标，求出平面A 1D 1F 的法向量，然后证明AE →与法向量共线．【自主解答】如图所示，建立空间直角坐标系，设正方体的棱长为1，则A (1,0,0)，E ⎝ ⎛⎭⎪⎫1，1，12，A 1(1,0,1)，D 1(0,0,1)，F ⎝ ⎛⎭⎪⎫0，12，0， ∴AE →＝⎝⎛⎭⎪⎫0，1，12，A 1D 1→＝(－1,0,0)，D 1F →＝⎝⎛⎭⎪⎫0，12，－1.设平面A 1D 1F 的法向量n ＝(x ，y ，z )， 则n ·A 1D 1→＝0，n ·D 1F →＝0， 即⎩⎪⎨⎪⎧－x ＝0，12y －z ＝0，解得x ＝0，y ＝2z .令z ＝1，则n ＝(0,2,1)． 又AE →＝⎝ ⎛⎭⎪⎫0，1，12，∴n ＝2AE →.∴n ∥AE →，即AE ⊥平面A 1D 1F .1．坐标法证明线面垂直有两种思路 方法一：(1)建立空间直角坐标系； (2)将直线的方向向量用坐标表示；(3)找出平面内两条相交直线，并用坐标表示它们的方向向量； (4)分别计算两组向量的数量积，得到数量积为0. 方法二：(1)建立空间直角坐标系； (2)将直线的方向向量用坐标表示； (3)求出平面的法向量；(4)判断直线的方向向量与平面的法向量平行．2．使用坐标法证明时，如果平面的法向量很明显，可以用方法二，否则常常选用方法一解决．[再练一题]2．如图3­2­15，长方体ABCD ­A 1B 1C 1D 1中，AB ＝AD ＝1，AA 1＝2，点P 为DD 1的中点，求证：直线PB 1⊥平面PAC .图3­2­15【证明】 依题设，以D 为坐标原点，如图所示，建立空间直角坐标系Dxyz ，则C (1,0,0)，P (0,0,1)，A (0,1,0)，B 1(1,1,2)，于是CA →＝(－1,1,0)，CP →＝(－1,0,1)，PB 1→＝(1,1,1)， ∴CA →·PB 1→＝(－1,1,0)·(1,1,1)＝0， CP →·PB 1→＝(－1,0,1)·(1,1,1)＝0，故CP →⊥PB 1→，CA →⊥PB 1→，即PB 1⊥CP ，PB 1⊥CA ， 又CP ∩CA ＝C ，且CP ⊂平面PAC ，CA ⊂平面PAC . 故直线PB 1⊥平面PAC .三垂线定理及其逆定理的应用在正方体ABCD ­A 1B 1C 1D 1中，求证：A 1C ⊥平面BDC 1.图3­2­16【自主解答】 在正方体中，AA 1⊥平面ABCD ，所以AC 是A 1C 在平面ABCD 内的射影，又AC ⊥BD ，所以BD ⊥A 1C .同理D1C是A1C在平面CDD1C1内的射影．所以C1D⊥A1C.又C1D∩BD＝D，所以A1C⊥平面BDC1.1．三垂线定理及其逆定理主要用于证明空间两条直线的垂直问题．对于同一平面内的两直线垂直问题也可用“平移法”，将其转化为空间两直线的垂直问题，用三垂线定理证明．2．当图形比较复杂时，要认真观察图形，证题的思维过程是“一定二找三证”，即“一定”是定平面和平面内的直线，“二找”是找平面的垂线、斜线和斜线在平面内的射影，“三证”是证直线垂直于射影或斜线．[再练一题]3．正三棱锥P­ABC中，求证：BC⊥PA.【证明】如图，在正三棱锥P­ABC中，P在底面ABC内的射影O为正三角形ABC的中心，连接AO，则AO是PA在底面ABC内的射影，且BC⊥AO，所以BC⊥PA.[探究共研型]利用向量证明面面垂直探究1【提示】只需求出两个平面的法向量，再看它们的法向量的数量积是否为0即可．探究2 在四面体ABCD中，AB⊥平面BCD，BC＝CD，∠BCD＝90°，∠ADB＝30°，E，F 分别是AC，AD的中点，求证：平面BEF⊥平面ABC.【提示】建系如图，取A (0,0，a )，则易得B (0,0,0)，C ⎝⎛⎭⎪⎫32a ，32a ，0，D (0，3a,0)，E ⎝⎛⎭⎪⎫34a ，34a ，a 2，F ⎝ ⎛⎭⎪⎫0，32a ，a 2.∵∠BCD ＝90°，∴CD ⊥BC .又AB ⊥平面BCD ，∴AB ⊥CD .又AB ∩BC ＝B ，∴CD ⊥平面ABC ，∴CD →＝⎝ ⎛⎭⎪⎫－32a ，32a ，0为平面ABC 的一个法向量．设平面BEF 的法向量n ＝(x ，y ，z )， 由n ·EF →＝0， 即(x ，y ，z )·⎝ ⎛⎭⎪⎫－34a ，34a ，0＝0，有x ＝y . 由n ·BF →＝0，即(x ，y ，z )·⎝ ⎛⎭⎪⎫0，32a ，a 2＝0，有32ay ＋a2z ＝0⇒z ＝－3y . 取y ＝1，得n ＝(1,1，－3)．∵n ·CD →＝(1,1，－3)·⎝ ⎛⎭⎪⎫－32a ，32a ，0＝0，∴n ⊥CD →，∴平面BEF ⊥平面ABC .如图3­2­17所示，在直三棱柱ABC ­A 1B 1C 1中，AB ⊥BC ，AB ＝BC ＝2，BB 1＝1，E为BB 1的中点，证明：平面AEC 1⊥平面AA 1C 1C .图3­2­17【精彩点拨】 要证明两个平面垂直，由两个平面垂直的条件，可证明这两个平面的法向量垂直，转化为求两个平面的法向量n 1，n 2，证明n 1·n 2＝0.【自主解答】由题意得AB ，BC ，B 1B 两两垂直．以B 为原点，BA ，BC ，BB 1分别为x ，y ，z 轴，建立如图所示的空间直角坐标系．A (2,0,0)，A 1(2,0,1)，C (0,2,0)，C 1(0,2,1)，E ⎝⎛⎭⎪⎫0，0，12，则AA 1→＝(0,0,1)，AC →＝(－2,2,0)，AC 1→＝(－2,2,1)，AE →＝⎝ ⎛⎭⎪⎫－2，0，12.设平面AA 1C 1C 的一个法向量为n 1＝(x 1，y 1，z 1)． 则⎩⎪⎨⎪⎧ n 1·AA 1→＝0，n 1·AC →＝0⇒⎩⎪⎨⎪⎧z 1＝0，－2x 1＋2y 1＝0.令x 1＝1，得y 1＝1.∴n 1＝(1,1,0)．设平面AEC 1的一个法向量为n 2＝(x 2，y 2，z 2)． 则⎩⎪⎨⎪⎧n 2·AC 1→＝0，n 2·AE →＝0⇒⎩⎪⎨⎪⎧－2x 2＋2y 2＋z 2＝0，－2x 2＋12z 2＝0，令z 2＝4，得x 2＝1，y 2＝－1.∴n 2＝(1，－1,4)． ∵n 1·n 2＝1×1＋1×(－1)＋0×4＝0. ∴n 1⊥n 2，∴平面AEC 1⊥平面AA 1C 1C .1．利用空间向量证明面面垂直通常可以有两个途径：一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直；二是直接求解两个平面的法向量，由两个法向量垂直，得面面垂直．2．向量法证明面面垂直的优越性主要体现在不必考虑图形的位置关系，恰当建系或用基向量表示后，只需经过向量运算就可得到要证明的结果，思路方法“公式化”，降低了思维难度．[再练一题]4．在正方体ABCD ­A 1B 1C 1D 1中，E 为CC 1的中点，证明：平面B 1ED ⊥平面B 1BD . 【证明】 以DA ，DC ，DD 1所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系．设正方体的棱长为1，则D (0,0,0)，B 1(1,1,1)，E ⎝⎛⎭⎪⎫0，1，12，DB 1→＝(1,1,1)，DE →＝⎝⎛⎭⎪⎫0，1，12，设平面B 1DE 的法向量为n 1＝(x ，y ，z )，则x ＋y ＋z ＝0且y ＋12z ＝0，令z ＝－2，则y ＝1，x ＝1，∴n 1＝(1,1，－2)．同理求得平面B 1BD 的法向量为n 2＝(1，－1,0)，由n 1·n 2＝0，知n 1⊥n 2，∴平面B 1DE ⊥平面B 1BD .[构建·体系]1．已知AB →＝(2,2,1)，AC →＝(4,5,3)，则平面ABC 的一个单位法向量为( ) A.⎝ ⎛⎭⎪⎫－13，－23，－23B ．⎝ ⎛⎭⎪⎫－13，23，－23C.⎝ ⎛⎭⎪⎫－13，23，23D ．⎝ ⎛⎭⎪⎫13，23，23 【解析】 设平面ABC 的法向量为n ＝(x ，y ，z )，则有⎩⎪⎨⎪⎧2x ＋2y ＋z ＝0，4x ＋5y ＋3z ＝0，取x ＝1，则y ＝－2，z ＝2.所以n ＝(1，－2,2)．由于|n |＝3，所以平面ABC 的一个单位法向量可以是⎝ ⎛⎭⎪⎫－13，23，－23.【答案】 B2．已知直线l 的方向向量是a ＝(3,2,1)，平面α的法向量是u ＝(－1,2，－1)，则l 与α的位置关系是( )A ．l ⊥αB ．l ∥αC ．l 与α相交但不垂直D ．l ∥α或l ⊂α【解析】 因为a ·u ＝－3＋4－1＝0，所以a ⊥u .所以l ∥α或l ⊂α. 【答案】 D3．已知点P 是平行四边形ABCD 所在的平面外一点，如果AB →＝(2，－1，－4)，AD →＝(4,2,0)，AP →＝(－1,2，－1)．对于结论： ①AP ⊥AB ； ②AP ⊥AD ；③AP →是平面ABCD 的法向量； ④AP →∥BD →.其中正确的是________．(填序号)【解析】 由于AP →·AB →＝－1×2＋2×(－1)＋(－1)×(－4)＝0，AP →·AD →＝(－1)×4＋2×2＋(－1)×0＝0，所以①②③正确．【答案】 ①②③4．如图3­2­18，已知PO ⊥平面ABC ，且O 为△ABC 的垂心，则AB 与PC 的关系是________.【导学号：15460075】图3­2­18【解析】 ∵O 为△ABC 的垂心， ∴CO ⊥AB .又∵OC 为PC 在平面ABC 内的射影， ∴由三垂线定理知AB ⊥PC . 【答案】 垂直5．在四棱锥P ­ABCD 中，底面ABCD 是正方形，侧棱PD 垂直于底面ABCD ，PD ＝DC ，E 是PC 的中点，作EF ⊥PB 于点F .求证：(1)PA ∥平面EDB ； (2)PB ⊥平面EFD .【证明】 建立如图所示的空间直角坐标系．D 是坐标原点，设DC ＝a .(1)连接AC 交BD 于G ，连接EG ，依题意得D (0,0,0)，A (a,0,0)，P (0,0，a )，E ⎝ ⎛⎭⎪⎫0，a 2，a 2.因为底面ABCD 是正方形，所以G 是此正方形的中心，故点G 的坐标为⎝ ⎛⎭⎪⎫a 2，a 2，0，所以EG →＝⎝ ⎛⎭⎪⎫a 2，0，－a 2. 又PA →＝(a,0，－a )，所以PA →＝2EG →，这表明PA ∥EG . 而EG ⊂平面EDB ，且PA ⊄平面EDB ， 所以PA ∥平面EDB .(2)依题意得B (a ，a,0)，PB →＝(a ，a ，－a )，DE →＝⎝ ⎛⎭⎪⎫0，a 2，a 2，所以PB →·DE →＝0＋a 22－a 22＝0，所以PB →⊥DE →，即PB ⊥DE .又已知EF ⊥PB ，且EF ∩DE ＝E ， 所以PB ⊥平面EFD .我还有这些不足：(1)________________________________________________________ (2)________________________________________________________ 我的课下提升方案：(1)________________________________________________________ (2)________________________________________________________学业分层测评 (建议用时：45分钟)[学业达标]一、选择题1．已知平面α的法向量为a ＝(1,2，－2)，平面β的法向量为b ＝(－2，－4，k )，若α⊥β，则k ＝( )A ．4B ．－4C ．5D ．－5【解析】 ∵α⊥β，∴a ⊥b ，∴a ·b ＝－2－8－2k ＝0.∴k ＝－5. 【答案】 D2．已知平面α的一个法向量是(2，－1,1)，α∥β，则下列向量可作为平面β的一个法向量的是( )A ．(4,2，－2)B ．(2,0,4)C ．(2，－1，－5)D ．(4，－2,2)【解析】 ∵α∥β，∴β的法向量与α的法向量平行，又∵(4，－2,2)＝2(2，－1,1)，故应选D.【答案】 D3．已知AB →＝(1,5，－2)，BC →＝(3,1，z )，若AB →⊥BC →，BP →＝(x －1，y ，－3)，且BP ⊥平面ABC ，则实数x ，y ，z 分别为( )A.337，－157，4 B ．407，－157，4C.407，－2,4 D ．4，407，－15【解析】 ∵AB →⊥BC →，∴AB →·BC →＝0，即3＋5－2z ＝0，得z ＝4， 又BP ⊥平面ABC ，∴BP →⊥AB →，BP →⊥BC →，则⎩⎪⎨⎪⎧x －1＋5y ＋6＝0，3x －1＋y －12＝0，解得⎩⎪⎨⎪⎧x ＝407，y ＝－157.【答案】 B4．已知平面α内有一个点A (2，－1,2)，α的一个法向量为n ＝(3,1,2)，则下列点P 中，在平面α内的是( )A ．(1，－1,1)B ．⎝ ⎛⎭⎪⎫1，3，32C.⎝⎛⎭⎪⎫1，－3，32D ．⎝⎛⎭⎪⎫－1，3，－32【解析】 对于B ，AP →＝⎝ ⎛⎭⎪⎫－1，4，－12，则n ·AP →＝(3,1,2)·⎝ ⎛⎭⎪⎫－1，4，－12＝0， ∴n ⊥AP →，则点P ⎝ ⎛⎭⎪⎫1，3，32在平面α内．【答案】 B5．设A 是空间一定点，n 为空间内任一非零向量，满足条件AM →·n ＝0的点M 构成的图形是( )A ．圆B ．直线C ．平面D ．线段【解析】 M 构成的图形经过点A ，且是以n 为法向量的平面． 【答案】 C 二、填空题6．已知直线l 与平面α垂直，直线l 的一个方向向量u ＝(1，－3，z )，向量v ＝(3，－2,1)与平面α平行，则z ＝________.【解析】 由题意知u ⊥v ，∴u ·v ＝3＋6＋z ＝0，∴z ＝－9. 【答案】 －97．已知a ＝(x,2，－4)，b ＝(－1，y,3)，c ＝(1，－2，z )，且a ，b ，c 两两垂直，则(x ，y ，z )＝________.【解析】 由题意，知⎩⎪⎨⎪⎧－x ＋2y －12＝0，x －4－4z ＝0，－1－2y ＋3z ＝0.解得x ＝－64，y ＝－26，z ＝－17. 【答案】 (－64，－26，－17)8．若A ⎝ ⎛⎭⎪⎫0，2，198，B ⎝ ⎛⎭⎪⎫1，－1，58，C ⎝ ⎛⎭⎪⎫－2，1，58是平面α内的三点，设平面α的法向量a ＝(x ，y ，z )，则x ∶y ∶z ＝________.【导学号：15460076】【解析】 因为AB →＝⎝ ⎛⎭⎪⎫1，－3，－74，AC →＝⎝⎛⎭⎪⎫－2，－1，－74，又因为a ·AB →＝0，a ·AC →＝0， 所以⎩⎪⎨⎪⎧x －3y －74z ＝0，－2x －y －74z ＝0，解得⎩⎪⎨⎪⎧x ＝23y ，z ＝－43y .所以x ∶y ∶z ＝23y ∶y ∶⎝ ⎛⎭⎪⎫－43y ＝2∶3∶(－4)． 【答案】 2∶3∶(－4) 三、解答题9.如图3­2­19，已知正方形ABCD 和矩形ACEF 所在的平面互相垂直，AB ＝2，AF ＝1，M 是线段EF 的中点．求证：AM ⊥平面BDF .图3­2­19【证明】 以C 为坐标原点，建立如图所示的空间直角坐标系，则A (2，2，0)，B (0，2，0)，D (2，0,0)，F (2，2，1)，M ⎝⎛⎭⎪⎫22，22，1.所以AM →＝⎝ ⎛⎭⎪⎫－22，－22，1，DF →＝(0, 2，1)，BD →＝(2，－2，0)．设n ＝(x ，y ，z )是平面BDF 的法向量， 则n ⊥BD →，n ⊥DF →，所以⎩⎪⎨⎪⎧n ·BD →＝2x －2y ＝0，n ·DF →＝2y ＋z ＝0⇒⎩⎨⎧x ＝y ，z ＝－2y ，取y ＝1，得x ＝1，z ＝－ 2. 则n ＝(1,1，－2)． 因为AM →＝⎝ ⎛⎭⎪⎫－22，－22，1.所以n ＝－ 2 AM →，得n 与AM →共线． 所以AM ⊥平面BDF .10．底面ABCD 是正方形，AS ⊥平面ABCD ，且AS ＝AB ，E 是SC 的中点．求证：平面BDE ⊥平面ABCD .【证明】法一 设AB ＝BC ＝CD ＝DA ＝AS ＝1，建立如图所示的空间直角坐标系Axyz ，则B (1,0,0)，D (0,1,0)，A (0,0,0)，S (0,0,1)，E ⎝ ⎛⎭⎪⎫12，12，12.连接AC ，设AC 与BD 相交于点O ，连接OE ，则点O 的坐标为⎝ ⎛⎭⎪⎫12，12，0.因为AS →＝(0,0,1)，OE →＝⎝ ⎛⎭⎪⎫0，0，12，所以OE →＝12AS →.所以OE ∥AS .又因为AS ⊥平面ABCD ， 所以OE ⊥平面ABCD . 又因为OE ⊂平面BDE ， 所以平面BDE ⊥平面ABCD .法二 设平面BDE 的法向量为n 1＝(x ，y ，z )， 因为BD →＝(－1,1,0)，BE →＝⎝ ⎛⎭⎪⎫－12，12，12，所以⎩⎪⎨⎪⎧n 1⊥BD →，n 1⊥BE →，即⎩⎨⎧n 1·BD →＝－x ＋y ＝0，n 1·BE →＝－12x ＋12y ＋12z ＝0，令x ＝1，可得平面BDE 的一个法向量为n 1＝(1,1,0)． 因为AS ⊥平面ABCD ，所以平面ABCD 的一个法向量为n 2＝AS →＝(0,0,1)． 因为n 1·n 2＝0，所以平面BDE ⊥平面ABCD .[能力提升]1．如图3­2­20，在正方体ABCD ­A 1B 1C 1D 1中，以D 为原点建立空间直角坐标系，E 为BB 1的中点，F 为A 1D 1的中点，则下列向量中，能作为平面AEF 的法向量的是( )图3­2­20A ．(1，－2,4)B ．(－4,1，－2)C ．(2，－2,1)D ．(1,2，－2)【解析】 设平面AEF 的一个法向量为n ＝(x ，y ，z )，正方体ABCD ­A 1B 1C 1D 1的棱长为1， 则A (1,0,0)，E ⎝ ⎛⎭⎪⎫1，1，12，F ⎝ ⎛⎭⎪⎫12，0，1.故AE →＝⎝ ⎛⎭⎪⎫0，1，12，AF →＝⎝ ⎛⎭⎪⎫－12，0，1.所以⎩⎪⎨⎪⎧AE →·n ＝0，AF →·n ＝0，即⎩⎪⎨⎪⎧y ＋12z ＝0，－12x ＋z ＝0，所以⎩⎪⎨⎪⎧y ＝－12z ，x ＝2z .当z ＝－2时，n ＝(－4,1，－2)，故选B. 【答案】 B2．如图3­2­21，在三棱柱ABC ­A 1B 1C 1中，侧棱AA 1⊥底面A 1B 1C 1，∠BAC ＝90°，AB ＝AC ＝AA 1＝1，D 是棱CC 1的中点，P 是AD 的延长线与A 1C 1的延长线的交点．若点Q 在线段B 1P 上，则下列结论正确的是( )图3­2­21A ．当点Q 为线段B 1P 的中点时，DQ ⊥平面A 1BD B ．当点Q 为线段B 1P 的三等分点时，DQ ⊥平面A 1BDC ．在线段B 1P 的延长线上，存在一点Q ，使得DQ ⊥平面A 1BDD ．不存在DQ 与平面A 1BD 垂直【解析】 以A 1为原点，A 1B 1，A 1C 1，A 1A 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则由已知得A 1(0,0,0)，B 1(1,0,0)，C 1(0,1,0)，B (1,0,1)，D ⎝⎛⎭⎪⎫0，1，12，P (0,2,0)，A 1B →＝(1,0,1)，A 1D →＝⎝⎛⎭⎪⎫0，1，12，B 1P →＝(－1,2,0)，DB 1→＝⎝⎛⎭⎪⎫1，－1，－12.设平面A 1BD 的法向量为n ＝(x ，y ，z )，则⎩⎨⎧n ·A1B →＝x ＋z ＝0，n ·A 1D →＝y ＋12z ＝0，取z ＝－2，则x ＝2，y ＝1，所以平面A 1BD 的一个法向量为n ＝(2,1，－2)．假设DQ ⊥平面A 1BD ，且B 1Q →＝λB 1P →＝λ(－1,2,0)＝(－λ，2λ，0)，则DQ →＝DB 1→＋B 1Q →＝⎝⎛⎭⎪⎫1－λ，－1＋2λ，－12，因为DQ →也是平面A 1BD 的法向量，所以n ＝(2,1，－2)与DQ →＝⎝ ⎛⎭⎪⎫1－λ，－1＋2λ，－12共线，于是有1－λ2＝－1＋2λ1＝－12－2＝14成立，但此方程关于λ无解．故不存在DQ 与平面A 1BD 垂直，故选D. 【答案】 D3.如图3­2­22，四棱锥P ­ABCD 的底面ABCD 是边长为1的正方形，PD ⊥底面ABCD ，且PD ＝1，若E ，F 分别为PB ，AD 中点，则直线EF 与平面PBC 的位置关系________．图3­2­22【解析】 以D 为原点，DA ，DC ，DP 所在直线为x 轴，y 轴，z 轴建立空间直角坐标系，则E ⎝ ⎛⎭⎪⎫12，12，12，F ⎝ ⎛⎭⎪⎫12，0，0，∴EF →＝⎝ ⎛⎭⎪⎫0，－12，－12，平面PBC 的一个法向量n ＝(0,1,1)，∵EF →＝－12n ，∴EF →∥n ，∴EF ⊥平面PBC . 【答案】 垂直4．如图3­2­23，在四棱锥P ­ABCD 中，底面ABCD 为直角梯形，且AD ∥BC ，∠ABC ＝∠PAD ＝90°，侧面PAD ⊥底面ABCD .若PA ＝AB ＝BC ＝12AD .图3­2­23(1)求证：CD ⊥平面PAC ；(2)侧棱PA 上是否存在点E ，使得BE ∥平面PCD ？若存在，指出点E 的位置并证明，若不存在，请说明理由．【解】 因为∠PAD ＝90°，所以PA ⊥AD .又因为侧面PAD ⊥底面ABCD ，且侧面PAD ∩底面ABCD ＝AD ，所以PA ⊥底面ABCD .又因为∠BAD ＝90°，所以AB ，AD ，AP 两两垂直．分别以AB ，AD ，AP 所在直线为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系．设AD ＝2，则A (0,0,0)，B (1,0,0)，C (1,1,0)，D (0,2,0)，P (0,0,1)． (1)AP →＝(0,0,1)，AC →＝(1,1,0)，CD →＝(－1,1,0)， 可得AP →·CD →＝0，AC →·CD →＝0，所以AP ⊥CD ，AC ⊥CD . 又因为AP ∩AC ＝A ，所以CD ⊥平面PAC .(2)设侧棱PA 的中点是E ，则E ⎝ ⎛⎭⎪⎫0，0，12，BE →＝⎝ ⎛⎭⎪⎫－1，0，12. 设平面PCD 的法向量是n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·CD →＝0，n ·PD →＝0，因为CD →＝(－1,1,0)，PD →＝(0,2，－1)，所以⎩⎪⎨⎪⎧－x ＋y ＝0，2y －z ＝0，取x ＝1，则y ＝1，z ＝2，所以平面PCD 的一个法向量为n ＝(1,1,2)．所以n ·BE →＝(1,1,2)·⎝ ⎛⎭⎪⎫－1，0，12＝0，所以n ⊥BE →. 因为BE ⊄平面PCD ，所以BE ∥平面PCD . 综上所述，当E 为PA 的中点时，BE ∥平面PCD .。