第三章 稳定性分析
- 格式:doc
- 大小:1013.50 KB
- 文档页数:24






第三章飞机的稳定性和操纵性3.1 飞机的稳定性在飞行中,飞机会经常受到各种各样的扰动,如气流的波动、发动机工作不稳定、飞行员偶然触动驾驶杆等。
这些扰动会使飞机偏离原来的平衡状态,而在偏离以后,飞机能否自动恢复原状,这就是有关飞机的稳定或不稳定的问题。
飞机的稳定性是飞机本身的一种特性,与飞机的操纵性有密切的关系。
例如,飞行员操纵杆、舵,需要用力的大小,飞机对杆、舵操纵的反应等,都与飞机的稳定性有关。
因此,研究飞机的稳定性是研究飞机操纵性的基础。
所谓飞机的稳定性,就是在飞行中,当飞机受微小扰动而偏离原来的平衡状态,并在扰动消失以后,不经驾驶员操纵,飞机能自动恢复原来平衡状态的特性。
3.1.1 纵向稳定性飞机的纵向稳定性是指飞机绕横轴的稳定性。
当飞机处于平衡飞行状态时,如果有一个小的外力干扰,使它的攻角变大或变小,飞机抬头或低头,绕横轴上下摇摆(也称为俯仰运动)。
当外力消除后,驾驶员如果不操纵飞机,而靠飞机本身产生一个力矩,使它恢复到原来的平衡飞行状态,我们就说这架飞机是纵向稳定的。
如果飞机不能靠自身恢复到原来的状态,就称为纵向不稳定的。
如果它既不恢复,也不远离,总是上下摇摆,就称为纵向中立稳定的。
飞机的纵向稳定性也称为俯仰稳定性。
飞机的纵向稳定性由飞机重心在焦点之前来保证。
影响飞机纵向稳定性的主要因素有飞机的水平尾翼和飞机的重心位置。
下面,我们首先来看一下水平尾翼是如何影响飞机的纵向稳定性的。
当飞机以一定的攻角作稳定的飞行时,如果一阵风从下吹向机头,使飞机机翼的攻角增大,飞机抬头。
阵风消失后,由于惯性的作用,飞机仍要沿原来的方向向前冲一段路程。
这时由于水平尾翼的攻角也跟着增大,从而产生了一个低头力矩。
飞机在这个低头力矩作用下,使机头下沉。
经过短时间的上下摇摆,飞机就可恢复到原来的飞行状态。
同样,如果阵风从上吹向机头,使机头下沉,飞机攻角减小,水平尾翼的攻角也跟着减小。
这时水平尾翼上产生一个抬头力矩,使飞机抬头,经过短时间的上下摇摆,也可使飞机恢复到原来的飞行状态。



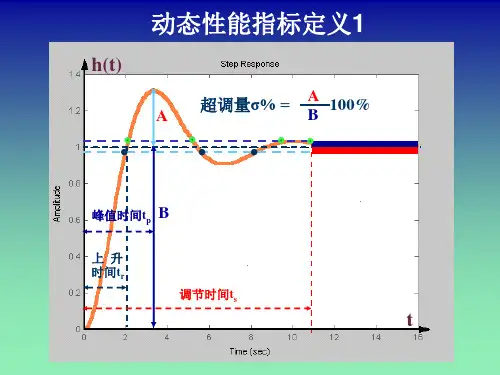
典型系统的时域响应和稳定性分析一、 实验目的1.研究二阶系统的特征参量(ξ、ωn )对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉Routh 判据,用Routh 判据对三阶系统进行稳定性分析。
4. 学习用电路系统研究一般控制系统的仿真实验方法二、 实验设备PC 机一台,Matlab ,Multisim (或PSpice)。
三、 实验原理及内容1.典型的二阶系统稳定性分析 (1) 结构框图:见图2-1图2-1(2) 对应的模拟电路图图2-2(3) 理论分析系统开环传递函数为:)1S T (S T K )1S T (S T K )S (G 101101+=+=;开环增益01T K K =。
(4) 实验内容先算出临界阻尼、欠阻尼、过阻尼时电阻R 的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中(图2-2),s 1T 0=, s T 2.01=,R 200K 1= R 200K =⇒系统闭环传递函数为:KS S KS S S W n n n 5552)(2222++=++=ωζωω 其中自然振荡角频率:R1010T K 1n ==ω;阻尼比:40R1025n =ω=ζ。
2.典型的三阶系统稳定性分析 (1) 结构框图图2-3(2) 模拟电路图图2-4(3) 理论分析系统的开环传函为:)1S 5.0)(1S 1.0(S R 500)S (H )S (G ++=(其中R 500K =),系统的特征方程为:0K 20S 20S 12S 0)S (H )S (G 123=+++⇒=+。
(4) 实验内容实验前由Routh 判断得Routh 行列式为:S 3 1 20 S 2 12 20K S 1 (-5K/3)+20 0S 0 20K 0为了保证系统稳定,第一列各值应为正数,所以有 ⎪⎩⎪⎨⎧>>+-0K 20020K 35得: 0 < K < 12 ⇒ R > 41.7KΩ 系统稳定K = 12 ⇒ R = 41.7KΩ 系统临界稳定 K > 12 ⇒ R < 41.7KΩ 系统不稳定四、 实验步骤1. 实验中阶跃信号幅值为1V 左右。
第三章 控制系统的李亚普诺夫稳定性主要内容: 1、 李亚普诺夫稳定性概念 2、 稳定性定理 3、 系统稳定性分析 4、 非线性系统稳定性分析难点:李亚普诺夫函数的构造§3.l 李亚普诺夫第二法的概述3.1.1物理基础系统的稳定性就是系统在受到外界干扰后,系统偏差量(被调量偏离平衡位置的数值)过渡过程的收敛性,用数学方法表示就是 ε≤∆∞→)(lim t x t式中)(t x ∆为系统被调量偏离其平衡位置的大小;ε为任意小的规定量。
物理事实:如果一个系统的某个平衡状态是渐近稳定的,即e t X X =∞→lim ,那么随着系统的运动,其贮存的能量将随着时间增长而衰减,直至趋于平衡状态而能量趋于极小值。
基本思想:李亚普诺夫引入了“广义能量”函数,称之为李亚普诺夫函数,表示为 V(x,t),它是状态n x x x ,,,21 和时间t 的函数。
对定常系统,“广义能量”函数则为V(X)。
如果考察的动态系统是稳定的,当存在),,,()(21n x x x V X V =对任意e X X ≠(平衡点)时,0V 0)(<>)(、X X V 成立,且对e X X =时,才有0V)(==)(X X V 。
关键:能否找到一个合适的李亚普诺夫函数。
数学基础:二次型及其定号性。
3.1.2二次型及其定号性1.二次型n 个变量n x x x ,,,21 的二次齐次多项式为222112222222121112112211121),,,(nnn n n n n n n n n n x a x x a x x a x x a x a x x a x x a x x a x a x x x V ++++++++++++= 称为二次型。
式中,),,2,1,(n k i a ik +是二次型的系数。
设ki ik a a =,既对称且均为实数。
用矩阵表示二次型较为方便,即[]PX X x x x a a a a a a a a a x x x X V T n nn n n n n n =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 2121222211121121,,,)( 必须指出,二次型是一个标量,最基本的特性就是它的定号性,也就是V(X)在坐标原点附近的特性。
(1)正定性当且仅当X=0时,才有V(X)=0;对任意非零X ,恒有V(X)>0,则V(X)为正定。
(2)负定性如果V(X)是负定的,或仅当X=0时,才有V(X)=0;对任意非零X ,恒有V(X)<0,则V(X)为负定。
(3)正半定性与负半定性 如果对任意0≠X ,恒有0)(≥X V ,则V(X)为正半定或称准正定。
如果对任意0≠X ,恒有0)(≤X V ,则V(X)为负半定或称准负定。
(4) 不定性如果无论取多么小的零点的某个邻域,V(X)可为正值也可为负值,则V(X)为不定。
2. 赛尔维斯特准则①二次型PX X X V T =)(或对称矩阵P 为正定的充要条件是P 的主子行列式均为正,即⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n n n a a a a a a a a a P 212222111211 如果,0,,0,0222112112111>=∆>=∆>=∆P a a a a a n则P 为正定,即V(X)正定。
②二次型PX X X V T =)(或对称阵P 为负定的充要条件是P 的主子行列式满足)(0为奇数i i <∆;n ,,2,1i )0(i i =>∆为偶数。
§3.2 李亚普诺夫意义下的稳定性3.2.1平衡点的概念 系统描述为),(t X f X= 式中 X 为n 维状态向量。
当在任意时间都能满足 0),(=t X f e (3.1)时称为系统的平衡状态。
凡满足式(3.1)的一切值均是系统的平衡点,对于线性定常系统,),(AX t X f X == A 为非奇异时,X=0是其唯一的平衡状态;对于非线性系统,有一个或多个平衡状态。
由式(3.1)可知,在系统的平衡点,状态变量的变化率为0,由古典控制理论知道,该点即为奇点,因此,系统微分方程式的奇点代表的就是系统在运动过程中的平衡点。
任何彼此孤立的平衡点,均可以通过坐标的变换,将其移到坐标原点,这就是经常以坐标原点作为平衡状态来研究的原因,因此常用的连续系统的平衡状态表达式为 0),0(=t f3.2.2李亚普诺夫定义下的稳定性下面用二维空间图3.1来说明李亚普诺夫定义下的稳定性。
稳 定渐近稳定不稳定图 3.1)(εS1.稳定与一致稳定设e X 为动力学系统),(t X f X= 的一个孤立平衡状态。
如果对球域)(εS 或任意正实数0>ε,都可找到另一个正实数),(0t εδ或球域)(δS ,当初始状态X 0满足),(00t X X e εδ≤-时,对由此出发的X的运动轨迹有ε≤-∞→e t X X lim ,则此系统为李亚普诺夫意义下的稳定。
如果δ与初始时刻t 0无关,则称平衡状态e X 为一致稳定。
2.渐近稳定和一致渐近稳定设e X 为动力学系统),(t X f X= 的孤立平衡状态,如果它是稳定的,且从充分靠近e X 的任一初始状态X 0出发的运动轨迹有0lim =-∞→e t X X 或),,2,1(0)(lim n i x x ie i t ==-∞→,即收敛用于平衡状态e X ,则称平衡状态e X 为渐近稳定。
如果δ与初始时刻t 0无关,则称平衡状态e X 为一致渐近稳定。
渐近稳定性等价于工程意义上的稳定性。
如果对状态空间中的任意点,不管初始偏差有多大,都有渐近稳定特性。
即),,2,1(0)(lim n i x x ie i t ==-∞→对所有点都成立,称平衡状态为大范围渐近稳定。
可见,这样的系统只能有一个平衡状态。
由于线性定常系统有唯一解,所以如果线性定常系统是渐近稳定的,则它一定也是大范围内渐近稳定的。
在控制工程中,确定大范围内渐近稳定的范围是很重要的,因为渐近稳定性是个局部概念,知道渐近稳定的范围,才能明确这一系统的抗干扰程度,从而可设法抑制干扰,使它满足系统稳定性的要求。
3.不稳定如果平衡状态e X 既不是渐近稳定的,也不是稳定的,当0t t >并无限增大时,从X 0出发的运动轨迹最终超越)(εS 域,则称平衡状态e X 为不稳定的。
§3.3 李亚普诺夫稳定性定理定理3.1 设系统的状态方程为),(t X f X= 式中,)(0),0(0t t t f ≥=如果有连续一阶偏导数的标量函数),(t X V存在,并且满足以下条件: ),(t X V 是正定的;),(t X V是负定的。
则在原点处的平衡状态是渐近稳定的。
如果随着∞→X ,有∞→),(t X V ,则在原点处的平衡状态是在大范围内渐近稳定的。
例3.1 设系统方程为⎩⎨⎧+--=--=)()(22212122221121x x x x xx x x x x 试确定其平衡状态的稳定性。
解 很明显,原点)0,0(21==x x 是给定系统的唯一平衡状态,选取一个正定的标量函数V(X)为2221)(x x X V += 则 221122)(xx x x X V +=将系统方程代入上式得22221)(2)(x x X V +-= ( V(X)为正定) 又由于∞→X 时,∞→)(X V ,因此系统在平衡点(0,0)是大范围渐近稳定的。
定理3.2 设系统的状态方程为 ),(t X f X= 式中 )(0),0(0t t t f ≥=。
如果存在一标量函数V(X,t),它具有连续的一阶偏导数,且满足下列条件:),(t X V 是正定的;),(t X V是负半定的; ]),,,([00t t X t V Φ 对任意t 0和任意00≠x ,在0t t ≥时不恒等于零。
则在系统原点处的平衡状态是渐近稳定的。
如果还有∞→X 时,∞→),(t X V ,则为大范围渐近稳定。
式中的),,(00t X t Φ表示0t t =时从0x 出发的解轨迹。
由于),(t X V不是负定的,而只是负半定的,则典型点的轨迹可能与某个特定的曲面),(t X V 相切。
然而,由于]),,,([00t t X t V Φ 对于任意t 0和任意00≠X 在0t t ≥时不恒等于零,所以典型点就不可能保持在切点处(在切点上0),(=t X V),而必须运动到原点。
例3.2 设系统方程为21221x x x x x --== 确定系统平衡状态的稳定性。
解 显然,原点(0,0)为给定系统的唯一平衡状态。
选取标准型二次函数为李氏函数,即2222112221222),(),(x x x xx t X V x x t X V -=+=+= ( V(X,t)为正定) 当 0,021==x x 时,0),(=t X V 0,021=≠x x 时,0),(=t X V 因此),(t X V是负半定的。
下面我们进一步分析),(t X V 的定号性,即当0,021=≠x x 时,),(t X V 是否恒等于零。
由于222),(x t X V -= 恒等于零,必需要求22x 在02t t ≥时恒等于零,而22x 恒等于零又必需要求2x 恒等于零。
但从状态方程212x x x --= 来看,在0t t ≥时,要使022=x 和02=x ,必需满足1x 等于零的条件。
这表明),(t X V 只可能在原点)0,0(21==x x 处恒等于零,因此系统在原点处的平衡状态是渐近稳定的。
又由于∞→X 时,有∞→)(X V ,所以系统在原点处的平衡状态是大范围渐近稳定的。
若在例中选取如下正定函数为李氏函数,即]2)[(21),(2221221x x x x t X V +++=则)(),(2221x x t X V +-= 是负定的。
而且当∞→X 时, ∞→),(t X V ,所以系统在原点处的平衡状态是大范围渐近稳定的。
由上分析看出,选取不同的李氏函数,可能使问题分析得出不同的结果。
上面第二种情况下的选择,消除了进一步对),(t X V判别的必要性。
定理3.3 设系统方程为 ),(t X f X= 式中,)(0),0(0t t t f ≥=。
如果存在一个标量函数),(t X V ,它具有连续的一阶偏导数,且满足下列条件: ),(t X V 是正定的;),(t X V是负半定的,但在某一X 值恒为零。
则系统在原点处的平衡状态在李亚普诺夫定义下是稳定的,但非渐近稳定。
这时系统可以保持在一个稳定的等幅振荡状态上。
例3.3 系统方程为1221x xKx x-== 试确定系统平衡状态的稳定性。
解 显然,原点为平衡状态。
选取正定函数为李氏函数,即)(),(2221Kx x t X V += (K>0)则 02222),(21212211=-=+=x Kx x Kx xKx x x t X V 由上式可见,),(t X V在任意X 值上均可保持为零,则系统在李亚普诺夫定义下是稳定的,但不是渐近稳定的。