武汉科技大学_信号与系统习题精解第7章
- 格式:doc
- 大小:1.08 MB
- 文档页数:15

第1章 信号及信号的时域分析1.1本章要点本章在时域范围内讨论信号的分类和信号的基本运算,通过本章的学习,读者应该了解信号的各种分类、定义及相关波形;了解各类常用信号及其性质,掌握几种奇异信号的特性及运算方法;了解和掌握信号的基本运算方法,深刻理解卷积与输入、输出信号和系统之间的物理关系及其性质,为后续课程打下牢固的基础。
1、信号的分类(1)连续信号与离散信号一个信号,如果在连续时间范围内(除有限个间断点外)有定义, 就称该信号在此区间内为连续时间信号,简称连续信号。
仅在离散时间点上有定义的信号称为离散时间信号,简称离散信号。
(2)确定信号与随机信号确定信号是指能够以确定的时间函数表示的信号。
即给定某一时间值,就能得到一个确定的信号值。
随机信号是时间的随机函数,即给定某一时间值,其函数值并不确定的信号。
(3)周期信号与非周期信号对于连续信号)(t f ,若存在0>T ,使得)()(t f rT t f =+,r 为整数,则称)(t f 为周期信号;对于离散信号)(n f ,若存在大于零的整数N ,使得)()(n f rN n f =+,r 为整数,则称)(n f 为周期信号。
不满足周期信号定义的信号称为非周期信号。
① 几个周期信号相加而成的信号的周期问题几个周期信号相加,所产生的信号可能是周期信号,也可能是非周期信号,这主要取决于几个周期信号的周期之间是否存在最小公倍数0T 。
以周期分别为1T 、2T (角频率分别为21,ΩΩ)的两个信号相加产生的信号()t f 为例,如果===ΩΩ211221n n T T 有理数,21,n n 均为整数,则()t f 为周期信号,其周期0T 为 22112211022Ω=Ω===ππn n T n T n T (1-1) ② 离散正(余)弦信号的周期问题时域连续的正(余)弦信号一定是周期信号,但时域离散的正(余)弦信号不一定是周期信号,要求周期N 为正整数。




7-1解 对于(a)图 (1)流图性质简化:21bx E x +=312dx ax x +=()32dx bx E a ++= ⇒ abdx aE x -132+=123ex cx x +=()22bx E e cx ++=()abdx aE be c eE -13+++=()()ab aE be c eE ab d be c x ---1113++=⎪⎭⎫⎝⎛+ R x =3所以 bedcd ab ace bed cd ab bea ac abe e E R H -------11+=++==(2)按梅森公式:图(a)有三个环路,环路增益为:edb cd ab 所以ebd cd ab ---1=∆图(a )有二条前向通路,通路增益为ac e ,且与各环路都相接触,即各特征行列式的余子式都为1,1=i ∆ 。
所以按梅森公式bedcd ab ace E R H ---1+==对于图(b ) (1)流图性质简化:221dx bE x +=()221112dx bE c aE cx aE x ++=+= ⇒ cdcbE aE x -1212+=2ex R = 所以 11-ae H cd =21-cbeH cd= (2)按梅森公式:图(b )有一个环路,环路增益为:cd对输入1E 有一条前向通路,通路增益为ae ,所以11-aeH cd =对输入2E 有一条前向通路,通路增益为cbe ,所以21-cbeH cd=7—2解()()()()()()()()()⎪⎩⎪⎨⎧++=++=t e t e t t t t e t e t t 21212211142783λλλλλ--()()()t t t r 1132λλ+=7—3解(1)模拟框图:题7—3解图1状态方程与输出方程:()()()()()()⎩⎨⎧+=+=+n e n n n n n 21221311λλλλλ-- ()()n n y 1λ= (2)模拟框图:题7-3解图2状态方程与输出方程:()()()()()()()()()()()()()⎪⎪⎩⎪⎪⎨⎧++=+=+=+=+4-3-4-2-7-3-111143214433221n e n e n n n n n n n n n n n λλλλλλλλλλλ ()()()()()()()()4-3-4-2-7-3-143214n e n e n n n n n n y ++=+=λλλλλ7—4解(1)系统函数可以改写为子系统相乘和相加形式如下()⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛++⨯⨯=5121115s s s s H -, ()53426521++++=s s s s H - 由上两式可以画出级联和并联形式流图()t e 1-()t 1-1-(a )()t e ()t r (b )题7—4解图1(2)系统函数可以改写为子系统相乘和相加形式如下()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛++=41311111s s s s H -- ()438323161+++++=s s s s H -- 由上两式可以画出级联和并联形式流图()t e 1-()t 1-1-(a)()t e ()t r 1-(b )题7—4解图27—5解(a )两条前向通路,三个环路,通路和环路间都接触.41321521413211H H H H H H H H H H H H H H ---+=(b)一条前向通路,三个环路,通路与所有环路都接触,有两个不接触环路。

230第10章 无限冲激响应数字滤波器的设计10.1 本章要点1、IIR 数字滤波器设计的基本概念及方法(1)IIR 数字滤波器的性能指标数字滤波器的频率响应)(ωj e H 可表示为:)()()(ωϕωωj j j e e H e H =式中,)(ωj e H 称为幅频特性,表示信号通过滤波器后各频率成分的衰减情况;)(ωϕ称为相频特性,反映各频率成分通过滤波器后在时间上的延时情况。
对IIR 数字滤波器,通常用幅频响应)(ωj e H 来描述性能指标。
需要注意的是数字滤波器的频率响应)(ωj e H 是以π2为周期的,滤波器的低频频带处于π2的整数倍附近,而高频频带处于π的奇数倍附近,这是数字滤波器与模拟滤波器的最大区别。
所以,一般只给出],0[π区间上的性能指标描述。
IIR 低通滤波器的幅频特性如图10-1所示。
图中,p ω和s ω分别称为通带截止频率和阻带截止频率。
通带频率范围为p ωω≤≤0,在通带中要求1)(11≤≤-ωδj e H ;阻带频率范围为πωω≤≤s ,在阻带中要求2)(δω≤j e H ;从p ω到s ω称为过渡带,在过渡带内,幅频响应平滑地从通带下降到阻带。
1δ在具体指标中往往用通带内允许的最大衰减p α表示,2δ用阻带内允许的最小衰减s α表示,p α和s α分别定义为:dB eH e H pj j p )()(lg 200ωα=dB eH e H sj j s )()(lg200ωα=如果将)(0j e H 归一化为1,则p α和s α可分别表示为:dBeH pj p )(lg 20ωα-= dBe H sj s )(lg 20ωα-=231当c p ωω=时,幅度下降到707.022≈,此时dB p 3=α,所以常称c ω为3dB 通带截止频率。
c ω是滤波器设计的重要参数之一。
图10-1 IIR 低通滤波器的幅频特性(2)IIR 数字滤波器的设计方法设计一个数字滤波器,可分为以下3步: ① 根据实际要求确定滤波器的性能指标。

武汉科技⼤学信号及系统期末试卷武汉科技⼤学考试卷(A 卷)课程:信号与系统(闭卷)(2014/05 )专业班级姓名学号⼀、填空题(每空2分,共20分)1.已知某系统的输出)(t r 与输⼊()e t 之间的关系为∑∞-∞=-=n nT t t e t r )()()(δ,其中T 为常数,则该系统是(线性/⾮线性)线性系统。
2.?-=+πππδdx x x )2()sin( -1 。
3.连续时间系统的传输算⼦为)2)(1(3)(+++=p p p p H ,则描述该系统的⽅程为()3()2()()3()r t r t r t e t e t ''''++=+,该系统的⾃然频率为 -1、-2 。
4.信号)f(t)=5cos(3t)+10cos(5t ππ的周期是_2_,其平均功率等于 62.5 ⽡。
5.信号)(t f 的最⾼频率为10m f kHz =,其奈奎斯特抽样频率s ω=4410π? 弧度/秒,信号(0.1)f t 的m f = 1kHz ,(0.1)f t 的奈奎斯特抽样间隔=s T 500s µ。
6.已知离散时间LTI 系统的单位函数响应为()cos(/3)()h k k k u k π=,则该系统为(稳定/不稳定)不稳定系统。
⼆、(12分)已知)(tf 的波形如图⼀所⽰。
)(t f (1)写出)(t f 的表达式;(2)画出()2(1)2tg t f =-+的波形; t(3)求()()dg t h t dt=的傅⾥叶变换。
图⼀解:(1)()[()(1)]f t t t t εε=-- (2分)(2分)(3 ()2()[()(2)]h t t t t δεε=--- (2分)2211()2[()](1)2(1)j j H j e e j j ωωωπδωωω--=-+-=-- (4分)三、(18分)已知)(t f 的频谱函数为)(ωj F ,其频谱图如图⼆所⽰。


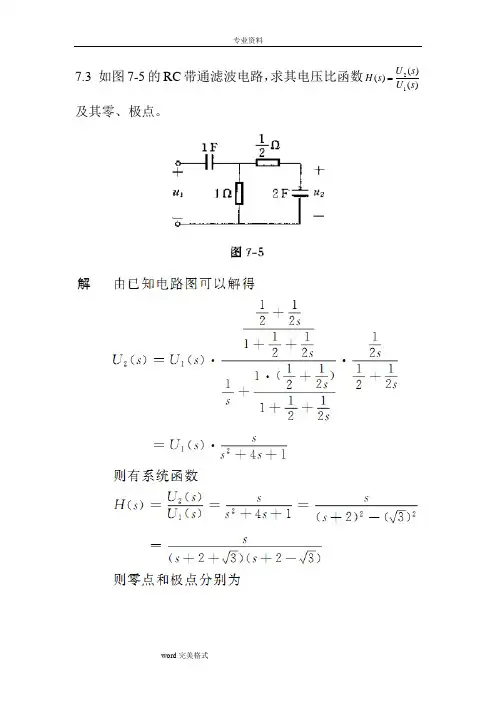
7.3 如图7-5的RC 带通滤波电路,求其电压比函数)()()(12s U s U s H 及其零、极点。
7.7 连续系统a 和b ,其系统函数)(s H 的零点、极点分布如图7-12所示,且已知当∞→s 时,1)(=∞H 。
(1)求出系统函数)(s H 的表达式。
(2)写出幅频响应)(ωj H 的表达式。
7.10 图7-17所示电路的输入阻抗函数)()()(11s I s U s Z =的零点在-2,极点在31j ±-,且21)0(=Z ,求R 、L 、C 的值。
7.14 如图7-27所示的离散系统,已知其系统函数的零点在2,极点在-0.6,求各系数a,b。
7.18 图7-29所示连续系统的系数如下,判断该系统是否稳定。
(1)3,210==a a ; (2)3,210-=-=a a ; (3)3,210-==a a 。
7.19 图7-30所示离散系统的系数如下,判断该系统是否稳定。
(1)1,2110-==a a ; (2)1,2110==a a ;(3)1,2110=-=a a 。
7.20 图7-31所示为反馈系统,已知44)(2++=s s ss G ,K 为常数。
为使系统稳定,试确定K 值的范围。
7.26 已知某离散系统的差分方程为)1()2()1(5.1)(-=---+k f k y k y k y(1) 若该系统为因果系统,求系统的单位序列响应h(k)。
(2) 若该系统为稳定系统,求系统的单位序列响应h(k),并计算输入)()5.0()(k k f k ε-=时的零状态响应)(k y zs 。
7.28 求图7-36所示连续系统的系统函数)(sH。
7.30 画出图7-40所示的信号流图,求出其系统函数)(sH。
解(a)由s域系统框图可得系统的信号流图如图7-41(a)。
流图中有一个回路。
其增益为(b)由s 域系统框图可得系统的信号流图如图7-41(b)。
流图中有一个回路。
170第7章 连续时间系统的频域分析7。
1 学习要点1 频率响应的定义频率响应可定义为系统零状态响应的傅里叶变换)(Ωj Y 与激励的傅里叶变换)(Ωj F 之比,即)()()(ΩΩΩj F j Y j H def=。
)(Ωj H 可写为:()ΩϕΩΩj e j H j H )()(=,其中,)(Ωj H 是输出与输入信号的幅度之比,称为幅频特性(或幅频响应);)(Ωϕ是输出与输入信号的相位差,称为相频特性(或相频响应). 2虚指数信号通过线性系统假设一个单位冲激响应为)(t h 的线性时不变系统,若有激励信号∞<<∞-=t e t f t j Ω)(则系统的零状态响应为:t j f e j H t y ΩΩ)()(=所以,当虚指数信号t j e Ω通过线性系统时,其零状态响应就是用t j e Ω乘以)(Ωj H 。
3 正弦信号通过线性系统若线性系统的激励为正弦信号∞<<∞-+==-t e e At A t f t j t j )(2cos )(ΩΩΩ则系统的零状态响应为:[])(cos )())((2)(ΩϕΩΩΩΩΩ+=+=-t j H A e e j H At y t j t j f所以,线性系统对正弦激励的响应为与激励同频率的正弦量,其振幅为激励的振幅与)(Ωj H 模值的乘积,其相位为激励的初相位与)(Ωj H 相位的和。
4 非正弦周期信号通过线性系统周期为T 的非正弦周期信号)(t f 可展开为:∑∞-∞==n tjn neF t f Ω)(式中,171dt e t f T F T T t jn n ⎰--=22)(1Ω则线性系统对该信号的零状态响应为:tjn n nf ejn H F t y ΩΩ)()(∑∞-∞==[])()()(ΩθΩϕΩΩn n t n j n ne jn H F ++∞-∞=∑=[])()(cos )(210ΩθΩϕΩΩn n t n jn H F F n n +++=∑∞=式中,)(Ωθn j n n e F F =,)()()(ΩϕΩΩn j e jn H jn H = 。
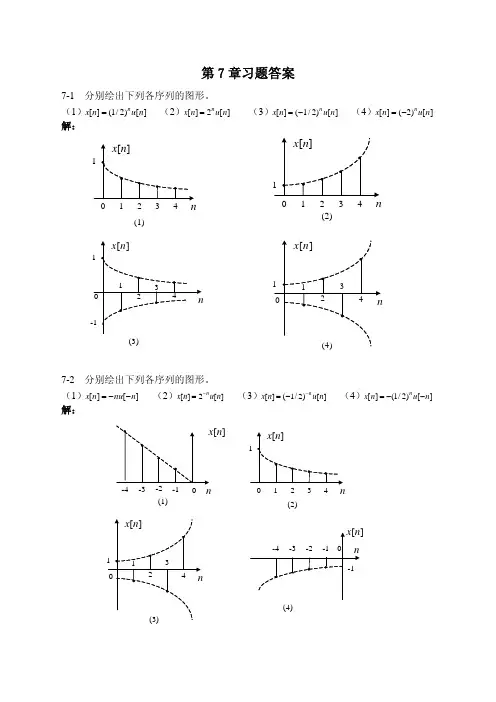
15- 分别绘出以下各序列的图形)()21()()1(n u n x n = )(2)()2(n u n x n =)()21()()3(n u n x n -= )()2()()4(n u n x n -=)1(2)()5(1-=-n u n x n )()21()()6(1n u n x n -=解)()1(n x 序列的图形如图5—1(a )所示。
)()2(n x 序列的图形如图5-1(b )所示。
)()3(n x 序列的图形如图5—1(c )所示。
)()4(n x 序列的图形如图5—1(d )所示。
)()5(n x 序列的图形如图5-1(e )所示。
(b)图5-1(a)(f)(e)(d)25- 分别绘出以下各序列的图形)()()1(n nu n x = )()()2(n nu n x --=)(2)()3(n u n x n -= )()21()()4(n u n x n --=)()21()()5(n u n x n --= )1()21()()6(1+=+n u n x n解) 序列的图形如图5—2(b)所示。
x()2(n 序列的图形如图5—2(c)所示.x))3(n(x 序列的图形如图5—2(d)所示. )4(n())5(n 序列的图形如图5-2(e)所示。
x()x 序列的图形如图5-2(f)所示。
())6(n(b)图5-2(c)(f)(e)(d)8-(a)35- 分别绘出以下各序列的图形)5sin()()1(πn n x =)510cos()()2(ππ-=n n x)5sin()65()()3(πn n x n =解)()1(n x 序列的图形如图5-3(a )所示。
)()2(n x 序列的图形如图5-3(b)所示。
)()3(n x 序列的图形如图5-3(c)所示。
图5-3(a)45- 判断以下各序列是否是周期性的,如果是周期性的,试确定其周期. )873sin()()1(ππ-=n A n x)8()()2(π-=ne n x j解)1(因为3147322==πππw 是有理数,所以)(n x 是周期性的,且周期为14。
1 / 30第一章 信号与系统1-1画出下列各信号的波形[式中)()(t t t r ε=]为斜升函数。
〔2∞<<-∞=-t et f t,)( 〔3)()sin()(t t t f επ=〔4)(sin )(t t f ε= 〔5)(sin )(t r t f = 〔7)(2)(k t f kε= 〔10)(])1(1[)(k k f kε-+=解:各信号波形为〔3)()sin()(t t t f επ= 〔4)(sin )(t t f ε= 〔5)(sin )(t r t f = 〔7)(2)(k t f k ε= 〔10)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
〔1)2()1(3)1(2)(-+--+=t t t t f εεε 〔2)2()1(2)()(-+--=t r t r t r t f 〔5)2()2()(t t r t f -=ε 〔8)]5()([)(--=k k k k f εε2 / 30〔11)]7()()[6sin()(--=k k k k f εεπ〔12)]()3([2)(k k k f k---=εε解:各信号波形为〔1)2()1(3)1(2)(-+--+=t t t t f εεε〔2)2()1(2)()(-+--=t r t r t r t f〔5)2()2()(t t r t f -=ε〔8)]5()([)(--=k k k k f εε〔11)]7()()[6sin()(--=k k k k f εεπ〔12)]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
〔2)63cos()443cos()(2ππππ+++=k k k f〔5)sin(2cos 3)(5t t t f π+=解:3 / 301-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
170第7章 连续时间系统的频域分析7.1 学习要点1 频率响应的定义频率响应可定义为系统零状态响应的傅里叶变换)(Ωj Y 与激励的傅里叶变换)(Ωj F 之比,即)()()(ΩΩΩj F j Y j H def=。
)(Ωj H 可写为:()ΩϕΩΩj ej H j H )()(=,其中,)(Ωj H 是输出与输入信号的幅度之比,称为幅频特性(或幅频响应);)(Ωϕ是输出与输入信号的相位差,称为相频特性(或相频响应)。
2虚指数信号通过线性系统假设一个单位冲激响应为)(t h 的线性时不变系统,若有激励信号∞<<∞-=t et f tj Ω)(则系统的零状态响应为:tj f ej H t y ΩΩ)()(=所以,当虚指数信号tj e Ω通过线性系统时,其零状态响应就是用tj e Ω乘以)(Ωj H 。
3 正弦信号通过线性系统若线性系统的激励为正弦信号∞<<∞-+==-t eeA t A t f tj tj )(2cos )(ΩΩΩ则系统的零状态响应为:[])(cos )())((2)(ΩϕΩΩΩΩΩ+=+=-t j H A eej H A t y tj tj f所以,线性系统对正弦激励的响应为与激励同频率的正弦量,其振幅为激励的振幅与)(Ωj H 模值的乘积,其相位为激励的初相位与)(Ωj H 相位的和。
4 非正弦周期信号通过线性系统周期为T 的非正弦周期信号)(t f 可展开为:∑∞-∞==n tjn neFt f Ω)(171式中,dt et f TF TTtjn n ⎰--=22)(1Ω则线性系统对该信号的零状态响应为:tjn n nf ejn H Ft y ΩΩ)()(∑∞-∞==[])()()(ΩθΩϕΩΩn n t n j n n ejn H F ++∞-∞=∑=[])()(cos )(210ΩθΩϕΩΩn n t n jn H FF n n+++=∑∞=式中,)(Ωθn j n n eF F =,)()()(ΩϕΩΩn j ejn H jn H = 。
所以,当周期信号)(t f 作用于线性系统时,其零状态响应仍为周期信号,且周期和激励信号的周期相同。
5 非周期信号激励下系统的响应当线性时不变系统的单位冲激响应为)(t h ,激励为)(t f 时,系统的零状态响应为:)(*)()(t h t f t y =对上式两端进行傅里叶变换,并利用时域卷积定理可得:)()()(ΩΩΩj H j F j Y =即系统零状态响应的频谱函数等于系统的频率响应函数与激励的频谱函数之乘积。
在求得)(Ωj Y 后,可利用傅里叶反变换求得系统的时域响应。
6 系统实现无失真传输的条件:(1)系统在全部频率范围(,)-∞+∞内为常数,即系统的通频带应为无穷大;(2)系统的相频特性应为通过原点的直线,即)(Ωϕ在整个频率范围内与Ω成正比。
设输入信号为)(t f ,那么经过无失真传输,输出信号应该为:()()d y t Kf t t =-,即输出信号的幅度是输入信号幅度的K 倍,而且比输入信号延时了d t 秒。
其幅频响应和相频响应分别为:⎭⎬⎫-==d t K j H ΩΩϕΩ)()(信号通过系统的延时为:ΩΩϕd d t d )(-=7 理想低通滤波器的定义具有图7-1所示幅频和相频特性的滤波器称为理想低通滤波器。
172图7-1 理想低通滤波器的幅频特性和相频特性可见,该滤波器对低于c Ω的频率成分不失真地全部通过,而对高于c Ω的频率成分完全抑制掉,称c Ω为截止角频率。
所以,c ΩΩ<的频率范围称为通带;c ΩΩ>的频率范围称为阻带。
理想低通滤波器的频率响应函数为:⎪⎩⎪⎨⎧><=-cc t j dKej H ΩΩΩΩΩΩ 0)(8 理想低通滤波器的冲激响应理想低通滤波器的冲激响应为:)]([)(d c c t t Sa K t h -=ΩπΩ取1=k ,其波形如图7-2所示。
图7-2 理想低通滤波器的冲激响应由图7-2可知,冲激响应)(t h 的波形不同于激励信号()t δ的波形,产生了严重失真。
另外,冲激响应)(t h 在0<t 的时候存在,这说明理想低通滤波器是一个非因果系统,是物理不可实现的系统。
9 理想低通滤波器的阶跃响应理想低通滤波器的阶跃响应为:)]([2)(d c t t Si KK t g -+=Ωπ取1=k ,)(t g 的波形如图7-3所示。
173图7-3 理想低通滤波器的阶跃响应由图7-3可知,理想低通滤波器的阶跃响应不像阶跃信号那样陡直上升,这表明阶跃响应的建立需要一段时间;同时波形出现过冲激振荡,这是由于理想低通滤波器是一个带限系统所引起的。
7.2 精选例题例1 已知一个连续LTI 系统可用)()(2)(t f t y dtt dy =+描述,利用傅里叶变换求下列输入信号作用下的输出)(t y : (1))()(t u e t f t -=(2))()(t u t f =解:对微分方程求傅里叶变换,得:)()(2)(ΩΩΩΩj F j Y j Y j =+频率响应为:ΩΩΩΩj j F j Y j H +==21)()()((1)输入)()(t u e t f t-=,其傅里叶变换为ΩΩj j F +=11)(,ΩΩΩΩΩj j j H j F j Y +-+==2111)()()(求其反变换可得)()()(2t u eet y tt---=。
(2)输入)()(t u t f =,其傅里叶变换为ΩΩπδΩj j F 1)()(+=,ΩΩΩπδΩΩΩπδΩΩΩj j j j j H j F j Y +⋅-⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=+⋅⎥⎦⎤⎢⎣⎡+==2121121211)()()()(174求其反变换可得)()1(21)(2t u et y t--=。
例2 如例2图所示的RC 电路,若激励电压源)(t U s 为单位阶跃信号)(t u ,求电容电压)(t U c 的零状态响应。
例2图解:电路的频率响应函数为:ΩααΩΩΩΩΩΩj RCj RC Cj R C j j U j U j H s c +=+=+==1111)()()(式中,RC1=α。
单位阶跃信号)(t u 的傅里叶变换为:ΩΩπδΩj j U s 1)()(+=可得零状态响应)(t U c 的频谱函数为:)()(1)()()()(ΩαΩαΩδΩααπΩΩπδΩααΩΩΩj j j j j j U j H j U s c +++=⎥⎦⎤⎢⎣⎡++== 考虑到冲激函数的取样性质,得:ΩαΩΩπδΩj j j U c +-+=11)()(取上式的傅里叶反变换,得输出电压)()1()()sgn(2121)(t u et u et t U ttc αα---=-+=式中,RC1=α。
例3 某LTI 系统的频率响应为ΩΩΩj j j H +-=22)(,若系统输入为)2cos()(t t f =,求该系+-()s U t RC+-()c U t175统的输出)(t y 。
解:因为[])2()2()(-++=ΩδΩδπΩj F ,所以系统的输出)(t y 的傅里叶变换)(Ωj Y 为:[][])2()2()2()2(22)()()(-++=-++⋅+-==ΩδΩδπΩδΩδπΩΩΩΩΩj j j j F j H j Y 得输出为t t y 2sin )(=。
例4 已知某一理想低通滤波器的频率响应为)()(240ΩΩG j H =,若输入信号为)10(cos )100cos(20)(42t t t f =,求输出()t y 。
解:对输入信号进行化简,得:t t t t f )100102cos(5)102100cos(5)100cos(10)(44-⨯+⨯++=即输入信号包含了三个频率成分:1000=Ω,41102100⨯+=Ω以及10010242-⨯=Ω。
由于系统频率响应是截止频率为120的理想低通滤波器,则只能让1000=Ω的频率分量通过,而1Ω和2Ω无法通过,故)100cos(10)(t t y =。
例5 已知系统框图如例5图所示,其中)(1t G 为门函数,子系统的单位冲激响应为:∑+∞-∞=-=n n t t h )2()(1δ, ttt hππ23s i n)(2=系统输入为t t e πcos )(=(+∞<<∞-t )。
(1)求子系统输出)(t ω的傅里叶变换;(2)证明)(t ω傅里叶系数为2cos )1(12ππk k C k -=;(3)求系统的稳态响应。
例5图解:(1)[])()()()(11t h t G t e t *⋅=ω,()tω()t (e t176因为 [])()()()(πΩδπΩδπΩ++-=↔j E t e ,⎪⎭⎫⎝⎛↔2)(1ΩSa t G 由频域卷积定理得:[]⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛*++-↔⋅22212)()(21)()(1πΩπΩΩπΩδπΩδππSa Sa Sa t G t e 再由时域卷积定理可得:)(2221)()(1ΩπΩπΩΩωj H Sa Sa j W t ⋅⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-=↔ 而∑+∞-∞=-=n n t t h )2()(1δ的周期2=T,角频率为πΩ=1,由于其单周期)()(10t t h δ=的傅里叶变换为1)(10=Ωj H ,则由周期信号的傅里叶级数与单周期信号傅里叶变换的关系得:∑∑+∞-∞==+∞-∞==⋅=n jn jn n n eej H Tt h πΩΩΩΩ21|)(1)(1101故其傅里叶变换为:∑∑+∞-∞=+∞-∞=-=-=n n n n j H )()(221)(1πΩδππΩπδΩ则)(12cos2)()(2cos2)(2221)(22221πΩδππΩδππππΩπΩπΩΩn nn n n n j H Sa Sa j W n n -⋅-=-⋅--=⋅⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-=∑∑∞+-∞=∞+-∞= (2)由(1)知)(t ω也是周期2=T ,角频率为πΩ=1的周期信号。
若)(t ω的傅里叶级数为1)(Ωωjn n neWt ∑+∞-∞==,则其傅里叶变换为:)(2)(πΩδπΩn Wj W n n-=∑+∞-∞=与(1)的结果相对比直接可得)1(2cos2n n W n -=ππ。
177(3)由傅里叶变换的对称性可知)(23sin)(32ΩπππG ttt h ↔=,即系统)(2t h 是一个理想低通滤波器,其截止频率为23π。
由(2)知)(t ω的基波频率为πΩ=1,则2次谐波和2次谐波以上的频率分量全部被滤除,只剩下直流分量和基波分量,即输出信号为:)c o s (211)(411)(t eet r tj tj πππππ+=++=-例6已知系统的单位冲激响应为t ttt h 1000cos 24sin )(⋅=π,输入t ttt f 997cos 25sin )(⋅=π,求系统的输出)(t y 。