
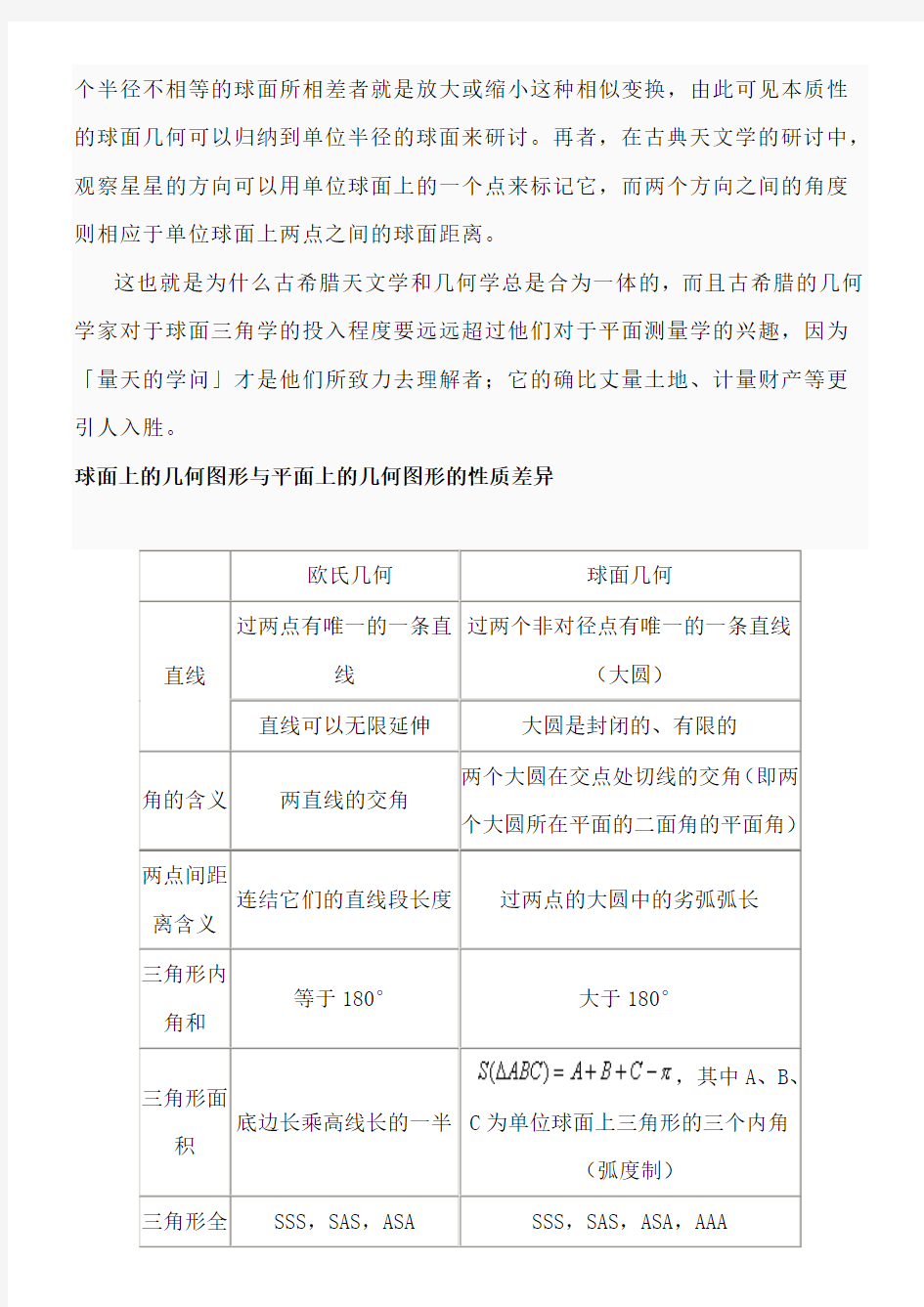
球面几何与欧式几何的比较
要说到几何,大多数人便会想到运用并流传了几千年的欧式几何,这是毋庸置疑的。欧式几何在我们的生活中运用太广泛了。从我们开始接触几何问题,和我们生活中所接触到的一些几何问题大部分都是欧式几何。欧式几何是几何学的一门分科,又称欧几里德几何。公元前3世纪,古希腊数学家欧几里德把人们公认的一些几何知识作为定义和公理,在此基础上研究图形的性质,推导出一系列定理,组成演绎体系,写出《几何原本》,形成了欧氏几何。欧式几何的传统描述是一个公理系统,通过有限的公理来证明所有的“真命题”。欧式几何共有五条公理,其中前四个都是可以通过各种方法来证明的,并被众人接受。唯有公理5使许多人不能被理解所接受。于是由此问题,我们又有了一个巨大的发现,也是人类历史上的重大转变。那就是非欧几何的出现。欧式几何所能解决的只限于平面,从而伟大的第五公理就这样在非欧几何中得证。
球面几何
球面几何学是在二维的球面表面上的几何学,也是非欧几何的一个例子。在平面几何中,基本的观念是点和线。在球面上,点的观念和定义依旧不变,但线不再是“直线”,而是两点之间最短的距离,称为最短线。在球面上,最短线是大圆的弧,所以平面几何中的线在球面几何中被大圆所取代。同样的,在球面几何中的角被定义在两个大圆之间。结果是球面三角学和平常的三角学有诸多不同之处。例如:球面三角形的内角和大于180度。
对比于通过一个点至少有两条平行线,甚至无穷多条平行线的双曲面几何学,通过特定的点没有平行线的球面几何学是椭圆几何学中最简单的模式。
球面几何学在航海学和天文学都有实际且重要的用途。球面乃是空间中最完美匀称的曲面。两个半径相等的球面可以用一个平移把它们叠合起来,而两
,其中A、B、C为单位球面上三角形的三个内角
(弧度制)
通过上面的比较,我们看到,球面上的几何是与平面几何不同的一种几何理论。平面几何最早由希腊数学家欧几里德整理成系统的理论。他的不朽之作《几何原本》不仅包含了平面几何,也包含了立体几何。为了纪念他对人类做出的伟大贡献,后来就把这种几何称为欧氏几何。虽然欧氏几何在我们的日常生活、生产实践与科学试验中有着广泛的应用,但是在某些领域或某种场合欧氏几何并不适用。例如在地球上要测量相距较远的两地之间的距离,或者较大范围的面积时,用欧氏几何的知识会产生很大的误差,而用球面几何的知识才能真实地反映出客观现实。球面上的几何是与欧氏几何不同的几何,所以叫做非欧几何。非欧几何往往也有很重要的实际应用价值,也是我们应该学习的重要理论。球面上的几何与欧氏几何有不相同之处,但他们之间也有一些共同特征。
球面上的几何与欧氏几何的共同特征
两种几何的这些相同之处,说明它们之间应该有某种内在的联系。
首先分析一下球面三角形的面积公式
把这个公式改写成
这个等式的左端称为球面三角形的角超,它反映出球面上的几何与平面几何的差距。在平面几何中三角形三内角之和等于,角超等于零。在球面上的几何中角超大于零。
不难看出当球面半径R无限增大时,球面逐渐趋向于平面,越来越小,即三角形的角超越来越小,球面三角形逐渐趋向于平面三角形,球面几何的性质逐渐接近于平面几何的性质。所以我们可以说:
当球面半径趋向于无穷大时,球面上的几何以平面几何为极限。
因为地球的半径非常大,当我们研究的范围相对于地球半径很小时,三角形的角超就一定很小。因此,可以用平面几何的知识来代替球面几何知识,所产生的误差很小。
非欧几何的诞生及其给我们的启示 摘要: 非欧几何的创立是数学史上最光辉的篇章,也是人类历史上一次伟大的思想解放的典范,它不仅带来了数学思想的深刻变革,也使人们的思想发生了极大的变化,使人们对真理、时空等一系列重大的哲学问题有了新的认识,对人类文化的发展产生了非同寻常的影响。数学史上,非欧几何占有特殊的地位.以非欧几何的发明过程为基本线索,探讨了其对数学学科本身、人类文化、哲学思想的影响;对数学科研者、数学教育工作者及高校学生的启示. 关键词: 非欧几何;罗巴切夫斯基几何;黎曼几何;几何原本; 1 非欧几何的发展史 1.1 问题的提出 非欧几何的发展源于2 000 多年前的古希腊数学家的欧几里得的《几何原本》.其中公设五是欧几里得自己提出的,它的内容是“若一条直线与两直线相交,且若同侧所交两内角之和小于两直角,则两直线无限延长后必相交于该侧的一点”.这一公设引起了广泛的讨论,因为它不如其他公理、公设那样简明,欧几里得本人也不满意这条公设,他在证完了所有不需要平行公设的定理后才使用它,怀疑它可能不是一个独立的公设,或许能用其它公设或公理代替.从古希腊时代开始到19 世纪的2000 多年来数学家们始终对这条公设耿耿于怀,孜孜不倦的试图解决这个问题.数学家们主要沿2 条研究途径前进:一条途径是寻找一条更为自明的命题代替平行公设;另一条途径是试图从其他9 条公理、公设推导出平行公设来.沿第一条途径找到的第五公设最简单的表述是1795 年苏格兰数学家普雷菲尔(J.Playfair 1748-1819)给出的:“过
直线外一点,有且只有一条直线与原直线平行”也就是我们今天中学课本里使用的平行公理.但实际上古希腊数学家普罗克鲁斯在公元5 世纪就陈述过它.然而问题是,所有这些替代公设并不比原来的第五公设更好接受,更“自然”.历史上第一个证明第五公设的重大尝试是古希腊天文学家托勒玫(Ptolemy,约公元150 年)做出的,后来普罗克鲁斯指出托勒玫的“证明”无意中假定了过直线外一点只能作一条直线与已知直线平行,这就是上面提到的普雷菲尔公设. 1.2 问题的解决 1.2.1 非欧几何的萌芽 沿第二条途径论证第五公设的工作在18 世纪取得突破性进展.首先是意大利人萨凯里(Saccharin 1667-1733)提出用归谬法证明第五公设,萨凯里从四边形ABCD 开始,如果角A 和角B 是直角,且AC=BD,容易证明角C等于角D.这样第五公设便等价于角C 和角D 是直角这个论断.萨凯里提出另2 个假设:(1)钝角假设:角C 和角D 都是钝角;(2)锐角假设:角C 和角D 都是锐角.最后在锐角假设下,萨凯里导出了一系列结果,因为与经验认识违背,使他放弃了最后结论.但是从客观上为非欧几何的创立提供了极有价值的思想方法,开辟了一条不同于前人的新途径.其后瑞士数学家兰伯特(Lambert1728-1777)所做的工作与萨凯里相似.他也考察了一类四边形,其中3 个角为直角,而第5 个角有3 种可能性:直角、钝角和锐角.他同样在锐角假设下得到“三角形的面积取决于其内角和;三角形的面积正比于平角与内角和的差.他认为只要一组假设相互没有矛盾,就提供了一种几何的可能.著名的法国数学家勒让德(A.M.Legendar1752-1833)对平行公设问题也十分关注,他得到的一个重要定理:“三角形内角之和不能大于两直角”.这预示着可能存在着一种新几何.19 世纪初,德国人萨外卡特(schweikart 1780-1859)使这种思想更加明朗化.他通过对“星形几何”的研究,指出:“存在两类几何:狭义的几何(欧氏几何)星形几何.在后一个里面,三角形有一个特点,就是三角形内角之和不等于两直角”.
欧几里得与欧几里得几何 亚历山大里亚的欧几里得(约公元前330年—前275年),古希腊数学家,被称为“几何之父”。他活跃于托勒密一世(公元前323年-前283年)时期的亚历山大里亚,他最著名的著作《几何原本》是欧洲数学的基础,提出五大公设,发展欧几里得几何,被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。 欧几里得是古希腊著名数学家、欧氏几何学的开创者。欧几里得生于雅典,当时雅典就是古希腊文明的中心。浓郁的文化气氛深深地感染了欧几里得,当他还是个十几岁的少年时,就迫不及待地想进入“柏拉图学园”学习。他在有攀滋入学园之后,便全身心地沉潜在数学王国里。他潜心求索,以继器粕拉图的学术为奋斗目标,除此之外,他哪儿也不去,什么也不干。熬翻阅和研究了柏拉图的所有著作和手稿,可以说,连柏拉图的亲传攀擎也没有谁能像他那样熟悉柏拉图的学术思想、数学理论。经过对柏拉图思想的深入探究,他得出结论:图形是神绘制的,所有一切籀象的逻辑规律都体现在图形之中。因此,对智慧的训练,就应该从戡图形为主要研究对象的几何学开始。他确实领悟到了柏拉图思想的要旨,并开始沿着柏拉图当年走过的道路,把几何学的研究作为自醺羽主要任务,并最终取得了世人敬仰的成就。 最早的几何学兴起于公元前7年的古埃及,后经古希腊等人传到古希腊的都城,又借毕达哥拉斯学派纂糯典。在欧几里得以前,人们已经积累了许多几何学的知识,然黔这些知识当中,存在一个很大的缺点和不足,就是缺乏系统性。大多数是片断、零碎的知识,公理与公理之问、证明与证明之间并没有什么很强的联系性,更不要说对公式和定理进行严格的逻辑论证和说明。因此,随着社会经济的繁荣和发展,特别是随着农林畜牧业的发展、土地开发和利用的增多,把这些几何学知识加以条理化和系统化,成为一整套可以自圆其说、前后贯通的知识体系,已经是刻不容缓,成为科学进步的大势所趋。欧几里得通过早期对柏拉图数学思想,尤其是几何学理论系统而周详的研究,已敏锐地察觉到了几何学理论的发展趋势。他下定决心,要在有生之年完成这一工作。为了完成这一重任,欧几里得不辞辛苦,长途跋涉,从爱琴海边的雅典古城,来到尼罗河流域的埃及新埠—亚历山大城,为的就是在这座新兴的,但文化蕴藏丰富的异域城市实现自己的初衷。在此地的无数个日日夜夜里,他一边收集以往的数学专著和手稿,向有关学者请教,一边试着著书立说,阐明自己对几何学的理解,哪怕是尚肤浅的理解。经过欧几里得忘我的劳动,终于在公元前300年结出丰硕的果实,这就是几经易稿而最终定形的《几何原本》一书。这是一部传世之作,几何学正是有了它,不仅第一次实现了系统化、条理化,而且又孕育出一个全新的研究领域——欧几里得几何学,简称欧氏几何。 不朽的平面几何学著作 《几何原本》是一部集前人思想和欧几里得个人创造性于一体的不朽之作。传到今天的欧几里得著作并不多,然而我们却可以从这部书详细的写作笔调中,看出他真实的思想底蕴。 全书共分13卷。书中包含了5条“公理”、5条“公设”、23个定义和467个命题。在每一卷内容当中,欧几里得都采用了与前人完全不同的叙述方式,即先提出公理、公设和定义,然后再由简到繁地证明它们。这使得全书的论述更加紧凑和明快。而在整部书的内容安排上,也同样贯彻了他的这种独具匠心的安排。它由浅到深,从简至繁,先后论述了直边形、圆、比例论、相似形、数、立体几何以及穷竭 法等内容。其中有关穷竭法的讨论,成为近代微积分思想的来源。仅仅从这些卷帙的内容安排上,我们就不难发现,这部书已经基本囊括了几何学从公元前7世纪的古埃及,一直到公元前4世纪——欧几里得生活时期——前后总共400多年的数学发展历史。这其中,颇有代表性的便是在第1卷到第4卷中,欧几里得对直边形和圆的论述。正是在这几卷中,他总结和发挥了前人的思维成果,巧妙地论证了毕达哥拉斯定理,也称“勾股定理”。即在一直角三角形中,斜边上的正方形的面积等于两条直角边上的两个正方形的面积之和。他的这一证明,从此确定了勾股定理的正确性并延续了2000多年。《几何原本》是一部在科学史上千古流芳的巨著。它不仅保存了许多古希腊
几何学基础简介 Lex Li 几何原本简介 古希腊大数学家欧几里德是与他的巨著——《几何原本》一起名垂千古的。这本书是世界上最著名、最完整而且流传最广的数学著作,也是欧几里德最有价值的一部著作。欧几里德把人们公认的一些事实列成定义和公理,以形式逻辑的方法,用这些定义和公理来研究各种几何图形的性质,从而建立了一套从公理、定义出发,论证命题得到定理得几何学论证方法,形成了一个严密的逻辑体系——几何学。而这本书,也就成了欧式几何的奠基之作。 作为基础的五条公理和公设 五条公理 1.等于同量的量彼此相等; 2.等量加等量,其和相等; 3.等量减等量,其差相等; 4.彼此能重合的物体是全等的; 5.整体大于部分。 五条公设 1.过两点能作且只能作一直线; 2.线段(有限直线)可以无限地延长; 3.以任一点为圆心,任意长为半径,可作一圆; 4.凡是直角都相等; 5.同平面内一条直线和另外两条直线相交,若在直线同侧的两个内角之和小于180°,则这两条直线经无限延长后在这一侧一定相交。 《几何原本》的主要内容 欧几里得的《几何原本》共有十三卷。 目录 第一卷几何基础 第二卷几何与代数 第三卷圆与角 第四卷圆与正多边形 第五卷比例
第六卷相似 第七卷数论(一) 第八卷数论(二) 第九卷数论(三) 第十卷无理量 第十一卷立体几何 第十二卷立体的测量 第十三卷建正多面体 各卷简介 第一卷:几何基础。重点内容有三角形全等的条件,三角形边和角的大小关系,平行线理论,三角形和多角形等积(面积相等)的条件,第一卷最后两个命题是毕达哥拉斯定理的正逆定理; 第二卷:几何与代数。讲如何把三角形变成等积的正方形;其中12、13命题相当于余弦定理。 第三卷:本卷阐述圆,弦,切线,割线,圆心角,圆周角的一些定理。 第四卷:讨论圆内接和外切多边形的做法和性质; 第五卷:讨论比例理论,多数是继承自欧多克斯的比例理论,被认为是"最重要的数学杰作之一" 第六卷:讲相似多边形理论,并以此阐述了比例的性质。 第五、第七、第八、第九、第十卷:讲述比例和算术的理论;第十卷是篇幅最大的一卷,主要讨论无理量(与给定的量不可通约的量),其中第一命题是极限思想的雏形。 第十一卷、十二、十三卷:最后讲述立体几何的内容. 从这些内容可以看出,目前属于中学课程里的初等几何的主要内容已经完全包含在《几何原本》里了。因此长期以来,人们都认为《几何原本》是两千多年来传播几何知识的标准教科书。 《几何原本》的意义和影响 在几何学发展的历史中,欧几里得的《几何原本》起了重大的历史作用。这种作用归结到一点,就是提出了几何学的“根据”和它的逻辑结构的问题。在他写的《几何原本》中,就是用逻辑的链子由此及彼的展开全部几何学,这项工作,前人未曾作到。《几何原本》的诞生,标志着几何学已成为一个有着比较严密的理论系统和科学方法的学科。 论证方法上的影响 关于几何论证的方法,欧几里得提出了分析法、综合法和归谬法。所谓分析法就是先假设所要求的已经得到了,分析这时候成立的条件,由此达到证明的步骤;综合法是从以前证明过的事实开始,逐步的导出要证明的事项;归谬法是在保留命题的假设下,否定结论,从结论的反面出发,由此导出和已证明过的事实相矛盾或和已知条件相矛盾的结果,从而证实原来命题的结论是正确的,也称作反证法。
浅谈解析几何的学习方法 ????高中数学中的解析几何内容学生之所以会觉得难是因为对几个常用公式、定理的含义并没有真正弄清楚,实际上如果能花时间把每个公式的推导过程研究一遍消化掉,那么学好它将不是什么疑难问题了。 ????我们知道,“数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休.”——我国着名数学家华罗庚。 ????作为学习解析几何的开始,我们引入了我国着名的数学家华罗庚的一句话,他告诉了我们“数”和“形”各自的特点和不足,从而强调了数形结合的重要性,尤其是在解析几何的学习过程中,我们始终都要注意运用数形结合的思想和方法。 ????当然,学习这一部分内容,只是了解这种思想也是不够的为此,就为大家介绍一下学习解析几何的方法和需要注意的几点。 一、夯实基础 1、正确理解定义 ??? 有些同学可能现在就会去翻书,去查定义,会说,回答这些问题还不容易嘛,我背一下不就可以了吗。可是,我要告诉大家——定义不是用来背的。????可能大家还没有理解这句话的意思,定义不是要你去死记硬背,而是要你去自己理解,去自己总结。
????教材上引入椭圆定义的时候花费了很大的篇幅,可它的本质是什么?与双曲线的定义又有怎样的相同点、不同点?椭圆、双曲线和抛物线这三个重要的圆锥曲线的统一定义我们又该如何去理解?这些,只有靠你自己总结出来,才能真正成为你自己的东西,在做题的时候,你才能应用自如。看一遍书上的定义,合上课本,想一想,如果让你来描述,你会怎么说。当你能够给别人将这些定义解释清楚的时候,你就已经很好的理解了这些定义,做题时,你就不会因为忽略了定义中隐含的条件而一筹莫展了。 2、比一比,学会总结 ????这一章我们介绍了三种圆锥曲线,它们有很多的相似之处,当然也有很多的不同,它们之间也有着千丝万缕的联系。学习完之后,自己比较一下,它们的定义、性质都有什么异同,哪些量是它们共有的,哪些量是某个圆锥曲线所特有的。当你比较完之后,再回过头来看这一章,你会发现,原来这一章的内容竟然如此的简单和清晰。 ????记住,一定要自己去总结哦!!别人给你的东西永远都是别人的,不是你自己的,只有自己总结过,才能清晰的把握问题的重点。 二、“数”与“形”要紧密联系 ????我们掌握了圆锥曲线的基础之后,就好比为我们的大厦打下了一个坚实的基础,现在,我们就可以正式建造我们的摩天大楼了! 1、让“数”直观
非欧几何简介 欧氏几何与球面几何的区别与联系 比较球面上的几何图形与平面上的几何图形的性质,我们可以总结出以下显著的差别,见表6-1: 表6-1 球面上的几何图形与平面上的几何图形的性质差异 ,其中A、B、C 为单位球面上三角形的三个内角(弧度 制) 通过上面的比较,我们看到,球面上的几何是与平面几何不同的一种几何理论。平面几何最早由希腊数学家欧几里德(Euclid,公元前300年左右)整理成
系统的理论。他的不朽之作《几何原本》不仅包含了平面几何,也包含了立体几何。为了纪念他对人类做出的伟大贡献,后来就把这种几何称为欧氏几何。球面上的几何是与欧氏几何不同的几何,所以叫做非欧几何。 球面上的几何与欧氏几何有不相同之处,但他们之间也有一些共同特征,见表6-2。 表6-2 球面上的几何与欧氏几何的共同特征 两种几何的这些相同之处,说明它们之间应该有某种内在的联系。 首先分析一下球面三角形的面积公式 把这个公式改写成 这个等式的左端称为球面三角形的角超,它反映出球面上的几何与平面几何的差距。在平面几何中三角形三内角之和等于,角超等于零。在球面上的几何中角超大于零。 不难看出当球面半径R无限增大时,球面逐渐趋向于平面,越来越小, 即三角形的角超越来越小,球面三角形逐渐趋向于平面三角形,球面几何的性质逐渐接近于平面几何的性质。所以我们可以说: 当球面半径趋向于无穷大时,球面上的几何以平面几何为极限。 因为地球的半径非常大,当我们研究的范围相对于地球半径很小时,三角形的角超就一定很小。因此,可以用平面几何的知识来代替球面几何知识,所产生的误差很小。 另一种非欧几何 通过前一小节的分析,我们发现三角形的三个内角之和的大小,在很大程度上反映了平面欧氏几何与球面几何的差别。当三角形的三个内角之和等于时,就是欧氏几何,当三角形的三个内角之和大于时,就反映出球面几何的主要特征。 有没有三角形三个内角之和小于的几何呢? 我们简单回顾一段几何发展史。在十七世纪以前,人们认为只有一种几何,就是欧氏几何,它是一切科学的基础。但是到了十七、十八世纪,数学家在对几何理论的基础进行深入研究时,首先把注意力集中在“平行公理”上。
初中几何常见模型解析 ?模型一:手拉手模型-旋转型全等 (1)等边三角形 ?条件:均为等边三角形 ?结论:①;②;③平分。(2)等腰 ?条件:均为等腰直角三角形 ?结论:①;②; ?③平分。 (3)任意等腰三角形 ?条件:均为等腰三角形 ?结论:①;②; ?③平分。 ?模型二:手拉手模型-旋转型相似 (1)一般情况 ?条件:,将旋转至右图位置 ?结论: ?右图中①; ?②延长AC交BD于点E,必有
(2)特殊情况 ?条件:,,将旋转至右图位置 ?结论:右图中①;②延长AC交BD于点E,必有; ③; ④; ⑤连接AD、BC,必有; ⑥(对角线互相垂直的四边形) ?模型三:对角互补模型 (1)全等型-90° ?条件:①;②OC平分 ?结论:①CD=CE; ②;③ ?证明提示: ①作垂直,如图,证明; ②过点C作,如上图(右),证明 ; ?当的一边交AO的延长线于点D时: 以上三个结论:①CD=CE(不变);② ;③ 此结论证明方法与前一种情况一致,可自行尝试。
(2)全等型-120° ?条件:①; ?②平分; ?结论:①;②; ?③ ?证明提示:①可参考“全等型-90°”证法一; ②如图:在OB上取一点F,使OF=OC,证明为等边三角形。 ?当的一边交AO的延长线于点D时(如上图右): 原结论变成:①;②; ③; 可参考上述第②种方法进行证明。 (3)全等型-任意角 ?条件:①;②; ?结论:①平分;②; ?③. ?当的一边交AO的延长线于点D时(如右上图): 原结论变成:①;②; ③; 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。
大学解析几何
收集于网络,如有侵权请联系管理员删除 空间解析几何 基本知识 一、向量 1、已知空间中任意两点),,(1111z y x M 和),,(2222z y x M ,则向量 12212121(,,)M M x x y y z z =---u u u u u u r 2、已知向量),,(321a a a a =→、),,(321b b b b =→,则 (1)向量→a 的模为232221||a a a a ++=→ (2)),,(332211b a b a b a b a ±±±=±→→ (3)),,(321a a a a λλλλ=→ 3、向量的内积→→?b a (1)><→→b a ,为向量→→b a ,的夹角,且π>≤≤<→→b a ,0 注意:利用向量的内积可求直线与直线的夹角、直线与平面的夹角、平面与平 面的夹角。 4、向量的外积→→?b a (遵循右手原则,且→→→⊥?a b a 、→→→⊥?b b a ) 321321 b b b a a a k j i b a → →→→→=?
收集于网络,如有侵权请联系管理员删除 5、(1)332211//b a b a b a b a b a ==? =?→→→→λ (2)00332211=++?=??⊥→→→→b a b a b a b a b a 二、平面 1、平面的点法式方程 已知平面过点),,(000z y x P ,且法向量为),,(C B A n =→ ,则平面方程为 0)()()(000=-+-+-z z C y y B x x A 注意:法向量为),,(C B A n =→ 垂直于平面 2、平面的一般方程0=+++D Cz By Ax ,其中法向量为),,(C B A n =→ 3、(1)平面过原点)0,0,0(? 0=++Cz By Ax (2)平面与x 轴平行(与yoz 面垂直)?法向量→n 垂直于x 轴 0=++?D Cz By (如果0=D ,则平面过x 轴) 平面与y 轴平行(与xoz 面垂直)?法向量→ n 垂直于y 轴0=++?D Cz Ax (如果0=D ,则平面过y 轴) 平面与z 轴平行(与xoy 面垂直)?法向量→ n 垂直于z 轴 0=++?D By Ax (如果0=D ,则平面过z 轴) (3)平面与xoy 面平行?法向量→ n 垂直于xoy 面0=+?D Cz
中考数学重难点专题讲座 第八讲 动态几何与函数问题 【前言】 在第三讲中我们已经研究了动态几何问题的一般思路,但是那时候没有对其中夹杂的函数问题展开来分析。整体说来,代几综合题大概有两个侧重,第一个是侧重几何方面,利用几何图形的性质结合代数知识来考察。而另一个则是侧重代数方面,几何性质只是一个引入点,更多的考察了考生的计算功夫。但是这两种侧重也没有很严格的分野,很多题型都很类似。所以相比昨天第七讲的问题,这一讲将重点放在了对函数,方程的应用上。其中通过图中已给几何图形构建函数是重点考察对象。不过从近年北京中考的趋势上看,要求所构建的函数为很复杂的二次函数可能性略小,大多是一个较为简单的函数式,体现了中考数学的考试说明当中“减少复杂性”“增大灵活性”的主体思想。但是这也不能放松,所以笔者也选择了一些较有代表性的复杂计算题仅供参考。 【例1】 如图①所示,直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l .将直线l 平移,平移后的直线l 与x 轴交于点D ,与y 轴交于点E. (1)将直线l 向右平移,设平移距离CD 为t (t≥0),直角梯形OABC 被直线l 扫过的面积(图中阴影部份)为s ,s 关于t 的函数图象如图②所示,OM 为线段,MN 为抛物线的一部分,NQ 为射线,且NQ 平行于x 轴,N 点横坐标为4,求梯形上底AB 的长及直角梯形OABC 的面积. (2)当24t <<时,求S 关于t 的函数解析式. 【思路分析】本题虽然不难,但是非常考验考生对于函数图像的理解。很多考生看到图
二的函数图像没有数学感觉,反应不上来那个M 点是何含义,于是无从下手。其实M 点就表示当平移距离为2的时候整个阴影部分面积为8,相对的,N 点表示移动距离超过4之后阴影部分面积就不动了。脑中模拟一下就能想到阴影面积固定就是当D 移动过了0点的时候.所以根据这么几种情况去作答就可以了。第二问建立函数式则需要看出当24t <<时,阴影部分面积就是整个梯形面积减去△ODE 的面积,于是根据这个构造函数式即可。动态几何连带函数的问题往往需要找出图形的移动与函数的变化之间的对应关系,然后利用对应关系去分段求解。 【解】 (1)由图(2)知,M 点的坐标是(2,8) ∴由此判断:24AB OA ==, ; ∵N 点的横坐标是4,NQ 是平行于x 轴的射线, ∴4CO = ∴直角梯形OABC 的面积为:()()11 2441222 AB OC OA +?=+?=..... (3分) (2)当24t <<时, 阴影部分的面积=直角梯形OABC 的面积-ODE ?的面积 (基本上实际考试中碰到这种求怪异图形面积的都要先想是不是和题中所给特殊图形有割补关系) ∴1 122 S OD OE =-? ∵ 1 42 OD OD t OE ==-, ∴()24OE t =- . ∴()()()2 1122441242S t t t =-?-?-=-- 284S t t =-+-. 【例2】 已知:在矩形AOBC 中,4OB =,3OA =.分别以OB OA ,所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与B C ,重合),过F 点的反比例函数(0)k y k x = >的图象与AC 边交于点E . (1)求证:AOE △与BOF △的面积相等;
欧式几何VS非欧几何 1什么是欧式几何? 2.欧式几何的来源?欧几里得 3欧式几何公理有哪些? 4欧式几何的缺陷——出现非欧几何 5什么是非欧几何? 包括?罗巴切夫斯基(俄)———罗式几何黎曼(德)————黎曼几何 6三种几何的关系
导出命题 第五条公理称为平行公理,可以导出下述命题: 通过一个不在直线上的点,有且仅有一条不与该直线相交的直线。平行公理并不像其他公理那么显然。许多几何学家尝试用其他公理来证明这条公理,但都没有成功。19世纪,通过构造非欧几里德几何,说明平行公理是不能被证明的。(若从上述公理体系中去掉平行公理,则可以得到更一般的几何,即绝对几何。) 从另一方面讲,欧式几何的五条公理并不完备。例如,该几何中的有定理:任意线段都是三角形的一部分。他用通常的方法进行构造:以线段为半径,分别以线段的两个端点为圆心作圆,将两个圆的交点作为三角形的第三个顶点。然而,他的公理并不保证这两个圆必定相交。因此,许多公理系统的修订版本被提出,其中有希尔伯特公理系统。 非欧氏几何 非欧氏几何产生于非欧式空间,而非欧式空间可以理解成扭曲了的欧式空间,可能它的坐标轴不再是直线,或者坐标轴之间并不 正交(即不成90度) 例子:欧式空间中的球面,对于在球面上爬行的蚂蚁来说就是非欧式空间的平面,它们在爬行的过程中不会感觉到球面的弯曲。当然在这样的一个球面上,欧式几何也不再成立,譬如:三角形的内角和不再是180度,而球面上两点之间的最短距离也不再是两点之间的连线(因为这时两点之间的的线段根本经 过球面)欧氏几何是平面,非欧几何是在一个不规则曲面上的 非欧几何学是一门大的数学分支,一般来讲,他有广义、狭义、通常意义这三个方面的不同含义。所谓广义式泛指一切和欧几里的几何学不同的几何学,狭义的非欧几何只是指罗式几何来说的,至于通常意义的非欧几何,就是指罗式几何和黎曼几何这两种几何。 欧几里得的《几何原本》提出了五条公设,长期以来,数学家们发现第五公设和前四个公设比较起来,显得文字叙述冗长,而且也不那么显而易见。 有些数学家还注意到欧几里得在《几何原本》一书中直到第二十九个命题中才用到,而且以后再也没有使用。也就是说,在《几何原本》中可以不依靠第五公设而推出前二十八个命题。 因此,一些数学家提出,第五公设能不能不作为公设,而作为定理?能不能依靠前四个公设来证明第五公设?这就是几何发展史上最著名的,争论了长达两千多年的关于“平行线理论”的讨论。 由于证明第五公设的问题始终得不到解决,人们逐渐怀疑证明的路子走的对不对?第五公设到底能不能证明? 到了十九世纪二十年代,俄国喀山大学教授罗巴切夫斯基在证明第五公设的过程中,他走了另一条路子。他提出了一个和欧式平行公理相矛盾的命题,用它来代替第五公设,然后与欧式几何的前四个公设结合成一个公理系统,展开
《几何学的本质》--- 几何学是人们在长期的生活实践中逐渐发展起来的理论思维成果之一。在它的启蒙阶段,现实中的物体形状和理论上的几何形状,一般是被混为一体或不加区分的,直到柏拉图时代,人们才开始注意到几何形状对于理论和现实的不同。人们所画在物体表面上的线都是有一定宽度的,它并非是几何学理论所意味的那种没有宽度的线;画在沙面上的三角形诸角,实际上是一些小块的面积,因此也不是理想的尖角。几何学概念的意义与体现它的现实事物的不相吻合,使柏拉图相信在超越现实事物的表面,一定有着“理念”事物存在,它们以十全十美的完善方式,显示出理想的几何属性。因而可靠的几何学知识,不是由现实事物来直接提供的,它需要人们对“理念”事物的一种“洞见”行为才能获得。 柏拉图的观点,代表了对几何学本质的早期见解,它使人们清楚地认识到,理想化的几何形状并不存在于人们生活的现实空间中。由于人们普遍认为欧几里德几何学中的每一条公理或公设,都不能从更为基本的前提中推导出来,而且每一条公理或公设对于处理现实事物都是有效的,所以,康德紧紧抓住几何学公理的不证自明性,认为几何学知识一定是通过逻辑以外的其它方式才能获得,并且是先天的和综合的。人们对现实事物所具有的几何特征
的认识,实际上是把现实事物置于几何学先天公理的构架上使之呈现的结果。同柏拉图一样,康德也把确定性的几何形状,同现实空间中的事物形状区分开来,但是他没有用理想的事物来解释几何学的本质,而是认为几何学知识是先于人类认识的,它们不能从人们的认识中得到解释和说明。 随着实验科学的发展,以及面对一系列通过实验所取得的丰硕成果,人们对科学理论的鉴别,逐渐倾向于依赖客观实验的检验。人们开始放弃柏拉图和康德的神秘主义几何学观点,并力图使几何学知识在现实空间中,能够得到客观实验的证明。高斯曾经测量过以三座山峰的顶端为顶点的三角形诸角,以试图验证这个三角形的内角和是否等于1800。后来爱因斯坦对此解释说,三角形内角和不等于1800,只有在很大的空间范围上才会明显,所以,对于我们附近的现实空间,欧几里得几何学是近似有用的。但是,高斯未能说明他所测量的三角形,为什么等同于理论意义上的几何三角形,爱因斯坦也没有区分三角形对于理论和现实的不同,他们回避了几何学中绝对理想化的几何形状,不存在于现实空间这一根本性的前提。理想化的直线和平面,在现实中没有与它们相对应的客观对象,研究直线平面几何形关系,应当只能针对理论意义上的直线和平面所构成的几何形及其几何关系。只有将几何学的研究
一、直线与方程基础: 1、直线的倾斜角α: [0,)απ∈ 2 、直线的斜率k : 21 21 tan y y k x x α-== -; 注意:倾斜角为90°的直线的斜率不存在。 3、直线方程的五种形式: ①点斜式:00()y y k x x -=-; ②斜截式:y kx b =+; ③一般式:0Ax By C ++=; ④截距式:1x y a b +=; ⑤两点式: 121 121 y y y y x x x x --=-- 注意:各种形式的直线方程所能表示和不能表示的直线。 4、两直线平行与垂直的充要条件: 1111:0l A x B y C ++=,2222:0l A x B y C ++=, 1l ∥2l 1221 1221 A B A B C B C B =???≠?; 1212120l l A A B B ⊥?+= . 5、相关公式: ①两点距离公式:11(,)M x y ,22(,)N x y ,
MN = ②中点坐标公式:11(,)M x y ,22(,)N x y , 则线段MN 的中点1122 ( ,)22 x y x y P ++; ③点到直线距离公式: 00(,)P x y ,:0l Ax By C ++=, 则点P 到直线l 的距离d = ; ④两平行直线间的距离公式:11:0l Ax By C ++=,22:0l Ax By C ++=, 则平行直线1l 与2l 之间的距离d = ⑤到角公式:(补充)直线1111:0l A x B y C ++=到直线2222:0l A x B y C ++=的角为 θ,(0,)(,)22 ππ θπ∈U ,则2112 tan 1k k k k θ-=+? .(两倾斜角差的正切) 二、直线与圆,圆与圆基础: 1、圆的标准方程:222()()x a y b r -+-=; 确定圆的两个要素:圆心(,)C a b ,半径r ; 2、圆的一般方程:220x y Dx Ey F ++++=,(22 40D E F +->); 3、点00(,)P x y 与圆222:()()C x a y b r -+-=的位置关系: 点00(,)P x y 在圆内? 22200()()x a y b r -+-<; 点00(,)P x y 在圆上? 22200()()x a y b r -+-=; 点00(,)P x y 在圆外? 222 00()()x a y b r -+->; 4、直线:0l Ax By C ++=与圆222:()()C x a y b r -+-=的位置关系: 从几何角度看: 令圆心(,)C a b 到直线:0l Ax By C ++=的距离为d , 相离?d r >;
欧几里得几何与非欧几何 摘要:欧几里得的《几何原本》奠定了几何学发展的基础, 随着逻辑推理的理论发展, 非欧几何在艰难中产生发展起来;其中少不了欧几里得、罗巴切夫斯基与黎曼在几何学上的巨大贡献,且两者几何学之间存在着严密的辩证关系。 关键词:欧几里得几何、几何原本、非欧几何、辩证关系 欧氏几何是人类创立的第一个完整的严密的(相对而言) 科学体系。它于公元前三世纪由古希腊数学家欧几里得完成,后来经历了两千多年的发展,对科学和哲学的影响是极其深远的。十九世纪二十年代,几何学发展史上出现了新的转折点,德国数学家高斯、匈牙利数学家亚·鲍耶和俄国数学家罗巴切夫斯基分别在1824年、1825年1826年各自独立地创立了非欧几何,其中以罗巴切夫斯基所发表的内容最完善,因此取名为罗氏几何学。1854年,德国数学家黎曼创立了黎曼几何。十九世纪末,德国数学家阂可夫斯基发展了黎曼几何,创立了四维空时几何学。1915年,爱因斯坦利用非欧几何——四维空间几何学作为工具创立了广义相对论, 不久广义相对论连同非欧几何为天文观察等科学实践所证实。从此,人们确认非欧几何是人类发现的伟大的自然科学真理。 一、欧几里得几何的发展 (一)古希腊前期几何学的发展为欧几里得几何的产生奠定了基础 在欧几里得时代以前,数学家与学者们就已经获得许多几何方面的成果,但大多数是零星的,有的对部分内容也作过一些整理加工,但不系统。面对前人留下的材料以及一些证明方法,欧几里得认真进行了总结、提练、筛选,以及分析、综合、归纳、演绎,集前人工作之大成,系统整理加工成巨著《几何原本》,所以说古希腊前期的几何学的发展为欧几里得几何的产生奠定了基础。 最早研究几何的一批人是爱奥尼亚学派,它的创始人是泰勒斯,据传他曾用一根已知长度的杆子,通过同时测量竿影和金字塔影之长,求出了金字塔的高度。人也把数学之成为抽象理论和有些定理演绎证明归功于他,如圆被直径二等分,等腰三角形两底角相等,两直线相交对顶角相等,两角及夹边对应相等的两个三角形全等,内接于半圆的角是直角等的论证。 对几何从经验上升到理论作出重要贡献的有毕达哥拉斯学派。他们注意研究抽象的数学概念,尤其对整数的性质有出色的研究。雅典的巧辩学派以著名的三等分任意角、化圆为方和倍立方三大难题为其研究中心。 柏拉图是那个时代影响最大的哲学家。柏拉图及其后继者把数学概念看作抽象图。柏拉图说数学概念不依赖于经验而自有其实在性。它们只能为人所发现,并非为人所发明或塑造。他是第一个把严密推理法则加以系统化的人,希腊人最早坚持数学里必须用演绎推理作求证的唯一方法,并使数学有别于所有其他知识领域或研究领域。柏拉图学派的最重要发现是圆锥曲线。还对不可公度量作过一些研究。这些都为欧几里得的研究开辟了道路。 欧多克斯是古希腊时代最大的数学家,他在数学上的第一个大贡献是关于比
欧几里德几何 简称“欧氏几何”。几何学的一门分科。公元前3世纪,古希腊数学家欧几里德把人们公认的一些几何知识作为定义和公理,在此基础上研究图形的性质,推导出一系列定理,组成演绎体系,写出《几何原本》,形成了欧氏几何。在其公理体系中,最重要的是平行公理,由于对这一公理的不同认识,导致非欧几何的产生。按所讨论的图形在平面上或空间中,分别称为“平面几何”与“立体几何”。 欧几里德几何指按照欧几里德的《几何原本》构造的几何学。 欧几里德几何有时就指平面上的几何,即平面几何。三维空间的欧几里德几何通常叫做立体几何。高维的情形请参看欧几里德空间。 数学上,欧几里德几何是平面和三维空间中常见的几何,基于点线面假设。数学家也用这一术语表示具有相似性质的高维几何。 公理描述 [编辑本段] 欧几里德几何的传统描述是一个公理系统,通过有限的公理来证明所有的“真命题”。 欧几里德几何的五条公理是: 任意两个点可以通过一条直线连接。 任意线段能无限延伸成一条直线。 给定任意线段,可以以其一个端点作为圆心,该线段作为半径作一个圆。 所有直角都全等。 若两条直线都与第三条直线相交,并且在同一边的内角之和小于两个直角,则这两条直线在这一边必定相交。 第五条公理称为平行公理,可以导出下述命题: 通过一个不在直线上的点,有且仅有一条不与该直线相交的直线。 平行公理并不像其他公理那么显然。许多几何学家尝试用其他公理来证明这条公理,但都没有成功。19世纪,通过构造非欧几里德几何,说明平行公理是不能被证明的。(若从上述公理体系中去掉平行公理,则可以得到更一般的几何,即绝对几何。) 从另一方面讲,欧几里德几何的五条公理并不完备。例如,该几何中的有定理:任意线段都是三角形的一部分。他用通常的方法进行构造:以线段为半径,分别以线段的两个端点为圆心作圆,将两个圆的交点作为三角形的第三个顶点。然而,他的公理并不保证这两个圆必定相交。因此,许多公理系统的修订版本被提出,其中有希尔伯特公理系统。 欧几里德还提出了五个“一般概念”,也可以作为公理。当然,之后他还使用量的其他性质。
高中数学空间几何体 一、选择题(本大题共12小题,每小题5分,共60分) 1.表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为( ) A. B. C. D. 2.如图所示是一个无盖的正方体盒子展开后的平面图,A、B、C是展开图上的三点,则在正方体盒子中,∠ABC为( ) A.1800 B.1200 C.600 D.450 3.已知三棱锥S-ABC的各顶点都在一个半径为r的球面上,球心O在AB 上,SO⊥底面ABC,,则球的体积与三棱锥体积之比是( ) A. B. C. D. 4.如图所示,一个空间几何体的正视图、侧视图、俯视图为全等的等腰
直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为( ) A.1 B. C. D. 5.一平面截球得到直径是6cm的圆面,球心到这个平面的距离是4cm,则该球的体积是( ) A. B. C. D. 6.半球内有一个内接正方体,则这个半球的体积与正方体的体积之比为( ) A. B. C. D. 7.一个四棱锥和一个三棱锥恰好可以拼成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等,设四棱锥、三棱锥、三棱柱的高分别为h1、h2、h3,则h1:h2:h3等于( ) A. B. C. D.
8.如图所示的一个5×4×4的长方体,阴影所示为穿透的三个洞,那么剩下的部分的体积是( ) A.50 B.54 C.56 D.58 9.一个正三棱锥的四个顶是半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( ) A. B. C. D. 10.如图用□表示1个正方体,用□(浅黑)表示两个正方体叠加,用□(深黑)表示三个立方体叠加,那么右图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
三角形三内角和 ——欧氏几何、罗氏几何、黎曼几何的比较 1840年,俄国数学家罗巴切夫斯基发表了一种新几何学.尽管高斯、波尔约和罗巴切夫斯基几乎同时各自独立地发现了这种新几何学,但由于罗巴切夫斯基第一个无所畏惧地公开发表了他的结果,所以,今天人们把这种新几何称为“罗氏几何”. 罗巴切夫斯基从1815年开始试图证明平行公理,几年的努力都失败了,失败使他逐渐认识到证明平行公理或第五公设是不可能的.1826年,身为大学教授的年轻的罗巴切夫斯基勇敢地抛弃了第五公设,提出了与欧几里得几何(简称欧氏几何)完全相反的公设:“过一点至少可以引两条直线与已知直线平行.”后来人们把这个公设叫做“罗氏公理”.由罗氏公理很容易推出以下结论:“过已知直线外一点可以引无数条直线与已知直线平行.” 罗巴切夫斯基保留了除平行公理以外的欧几里得的全部公理.如果不涉及与平行有关的内容,罗巴切夫斯基的新几何与欧几里得几何学没有任何不同.但是只要与平行有关,那么结果就相差甚远.下表对罗巴切夫斯基几何(简称罗氏几何)、欧氏几何不同的定理作了说明. 图7-11
欧氏几何说:“三角形的三内角和等于180 o.”现实生活中有没有这种几何模型呢?有!平面上的三角形的内角和就等于180 o,如图7-12左图.罗氏几何说“三角形的三内角和小于180o”.难道现实生活中也会有这样的几何模型吗?有!1868年意大利数学家贝特拉米找到了一种曲面,人们给它起名叫“伪球面”.在“伪球面”上可以证明:“三角形内角和小于180 o”,如图7-12中间的图. 图7-12 现实生活中有没有“三角形的内角和大于180 o”的几何学?有!这是德国著名数学家黎曼于1854年提出来的,如图7-12右图. 黎曼生于德国汉诺威,父亲是牧师,他遵照父亲的愿望进入哥廷根大学学习哲学和神学.可是进哥廷根大学后,他很快被数学所吸引.于是就放弃神学专攻数学,并成为大数学家高斯的学生.1851年他获得数学博士学位,博士论文受到高斯极高的评价.1859年他成为哥廷根大学的教授,1866年因患肺结核死于意大利,年仅40岁. 黎曼提出了一种与前两种几何完全不同的新几何,叫做“黎曼几何”.黎曼几何的模型是球面,在黎曼几何中“三角形内角之和大于180 o.” 后来,人们把罗氏几何和黎曼几何合在一起统称“非欧几何”.非欧几何在现代物理中,特别是相对论提出之后找到了具体用处,使得非欧几何并不像有些人说的是“想象中的几何”,而成了有着重要现实意义的几何学.
Geometry Geometry is all about shapes and their properties. If you like playing with objects, or like drawing, then geometry is for you! Geometry can be divided into: Plane Geometry is about flat shapes like lines, circles and triangles ... shapes that can be drawn on a piece of paper Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres. Hint: Try drawing some of the shapes and angles as you learn ... it helps. Point, Line, Plane and Solid A Point has no dimensions, only position A Line is one-dimensional A Plane is two dimensional (2D) A Solid is three-dimensional (3D)
Why? Why do we do Geometry? To discover patterns, find areas, volumes, lengths and angles, and better understand the world around us. Plane Geometry Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper). 2D Shapes Activity: Sorting Shapes Triangles Right Angled Triangles Interactive Triangles Quadrilaterals (Rhombus, Parallelogram, etc) Rectangle, Rhombus, Square, Parallelogram, Trapezoid and Kite Interactive Quadrilaterals Shapes Freeplay Perimeter