线性回归方程的求法

简单线性回归方程是一种基本的回归分析模型，它只涉及一个因变量和一个自变量，并且这两个变量之间呈线性关系。

简单线性回归方程的公式为：y=β0+β1x+ε，其中y是因变量，x是自变量，β0和β1是模型参数，ε是误差项。

这个公式表示的是，因变量y的期望值E(y)与自变量x和误差项ε之间的关系。

具体来说，E(y)=β0+β1x。

这个公式是通过最小二乘法等统计方法，根据样本数据拟合得到的。

简单线性回归方程的应用非常广泛，例如在经济学、生物学、医学等领域都有广泛的应用。

通过简单线性回归方程，我们可以分析两个变量之间的关联性，预测未来趋势，以及进行统计推断等。

高三线性回归方程知识点线性回归是数学中的一种方法，用于建立一个自变量与因变量之间的关系。

在高三数学中，线性回归方程是一个重要的知识点。

本文将介绍高三线性回归方程的基本概念、推导过程以及应用范围。

一、基本概念1. 线性回归方程线性回归方程，也叫作线性回归模型，表示自变量x和因变量y之间的关系。

它可以用如下的一般形式表示：y = β0 + β1x + ε其中，y表示因变量，x表示自变量，β0和β1表示模型中的参数，ε表示误差项。

2. 参数估计线性回归方程中的参数β0和β1需要通过观测数据进行估计。

常用的方法是最小二乘法，即通过最小化实际观测值和预测值之间的差异，来得到最优的参数估计值。

二、推导过程1. 求解参数通过最小二乘法，可以得到线性回归方程中的参数估计值。

具体推导过程包括以下几个步骤：（1）确定目标函数：将观测值和预测值之间的差异平方和作为目标函数。

（2）对目标函数求偏导：对目标函数分别对β0和β1求偏导，并令偏导数为0。

（3）计算参数估计值：根据求得的偏导数为0的方程组，解出β0和β1的值。

2. 模型拟合度评估在得到参数估计值之后，需要评估线性回归模型的拟合度。

常用的指标包括相关系数R和残差平方和SSE等。

相关系数R可以表示自变量和因变量之间的线性相关程度，取值范围在-1到1之间，越接近1表示拟合度越好。

三、应用范围线性回归方程在实际问题中有广泛的应用，例如经济学、统计学、社会科学等领域。

它可以用来分析自变量和因变量之间的关系，并预测未来的结果。

1. 经济学应用在线性回归模型中，可以将自变量设置为经济指标，例如GDP、通货膨胀率等，将因变量设置为某一经济现象的数值。

通过构建线性回归方程，可以分析不同经济指标对经济现象的影响，为经济决策提供参考依据。

2. 统计学应用线性回归方程是统计学中的一项重要工具。

通过对观测数据的拟合，可以得到参数估计值，并进一步分析自变量和因变量之间的关系。

统计学家可以利用线性回归分析建立统计模型，为实验数据的解释提供更为准确的结论。

回归方程公式研究回归方程的关键公式回归分析是一种用于描述两个或多个变量之间关系的统计方法。

在回归分析中，回归方程是研究的核心，它能够通过自变量的值来预测因变量的值。

本文将重点探讨回归方程的关键公式，帮助读者更好地理解回归分析的数学模型。

一、简单线性回归方程简单线性回归是回归分析中最简单的一种形式，它描述了两个变量之间的线性关系。

简单线性回归方程的数学形式为：Y = α + βX + ε其中，Y是因变量，X是自变量，α和β分别是回归方程的截距和斜率，ε是误差项。

β可以通过最小二乘法来进行估计，最小二乘估计的公式为：β = Σ((Xi - X¯)(Yi - Y¯)) / Σ(Xi - X¯)²其中，Xi和Yi分别代表第i个数据点的自变量和因变量的取值，X¯和Y¯分别代表自变量和因变量的平均值。

二、多元线性回归方程多元线性回归是在简单线性回归的基础上，引入了两个或多个自变量来描述因变量之间的关系。

多元线性回归方程的数学形式为：Y = α + β1X1 + β2X2 + ... + βnXn + ε其中，Y是因变量，X1、X2、...、Xn是自变量，α和β1、β2、...、βn分别是回归方程的截距和斜率，ε是误差项。

多元线性回归方程中的参数估计可以使用最小二乘法进行，公式为：β = (X'X)⁻¹X'Y其中，X是自变量矩阵，Y是因变量向量，(X'X)⁻¹代表(X'X)的逆矩阵，X'代表X的转置。

三、回归方程的解释回归方程的系数α和β可以用来解释自变量和因变量之间的关系。

截距α表示当自变量为0时因变量的取值，斜率β表示自变量每增加一个单位时，因变量的平均变化量。

此外，回归方程还可以通过R²来评估拟合优度，R²代表回归方程能够解释因变量变异性的比例，取值范围为0到1。

R²越接近1，说明回归方程对数据的拟合程度越好。

如何计算回归方程
计算回归方程的方法主要是使用最小二乘法。

最小二乘法是一种常用的回归分析方法，用于拟合一条直线或曲线与一组数据点的最佳拟合。

以简单线性回归为例，回归方程可以表示为`y = mx + b`，其中`y` 是因变量（或称为响应变量），`x` 是自变量（或称为解释变量），`m` 是斜率，`b` 是截距。

以下是计算回归方程的步骤：
1. 收集数据：收集自变量`x` 和因变量`y` 的一组数据点。

2. 计算均值：计算自变量和因变量的均值，分别记为`x_mean` 和`y_mean`。

3. 计算差值：对每个数据点，计算自变量`x` 和因变量`y` 与均值的差值，分别记为`dx` 和`dy`。

4. 计算乘积：对每个数据点，计算`dx * dy` 的乘积，记为`dx_dy`。

5. 计算平方差值：对每个数据点，计算`dx` 的平方，记为
`dx_squared`。

6. 计算斜率：计算斜率`m`，公式为`m = sum(dx_dy) / sum(dx_squared)`，其中`sum()` 表示求和。

7. 计算截距：计算截距`b`，公式为`b = y_mean - m * x_mean`。

8. 得到回归方程：将斜率`m` 和截距`b` 代入回归方程`y = mx + b`，得到最终的回归方程。

需要注意的是，以上步骤适用于简单线性回归，即自变量和因变量之间的关系可以用一条直线来拟合。

对于多元线性回归或非线性回归，计算回归方程的方法会有所不同。

另外，可以使用统计软件或编程语言的回归函数来自动计算回归方程，例如在Python中，可以使用NumPy或SciPy库的回归函数来计算回归方程。

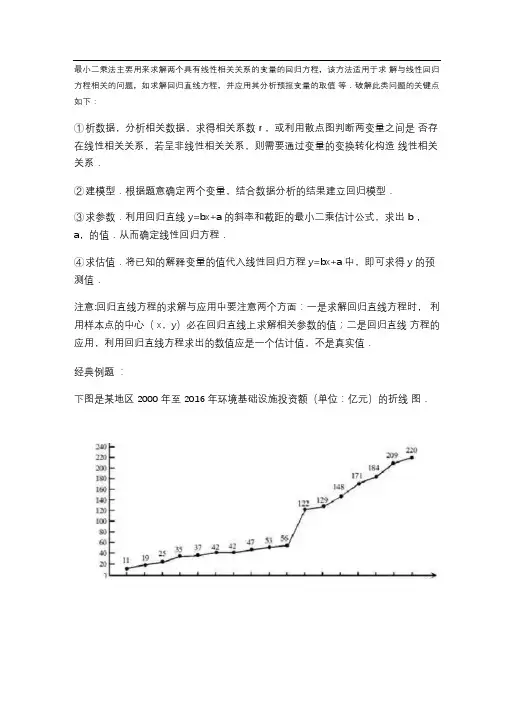
最小二乘法主要用来求解两个具有线性相关关系的变量的回归方程，该方法适用于求解与线性回归方程相关的问题，如求解回归直线方程，并应用其分析预报变量的取值等．破解此类问题的关键点如下：①析数据，分析相关数据，求得相关系数 r ，或利用散点图判断两变量之间是否存在线性相关关系，若呈非线性相关关系，则需要通过变量的变换转化构造线性相关关系．②建模型．根据题意确定两个变量，结合数据分析的结果建立回归模型．③求参数．利用回归直线 y=bx+a 的斜率和截距的最小二乘估计公式，求出 b ，a，的值．从而确定线性回归方程．④求估值．将已知的解释变量的值代入线性回归方程 y=bx+a 中，即可求得 y 的预测值．注意:回归直线方程的求解与应用中要注意两个方面：一是求解回归直线方程时，利用样本点的中心（ x，y）必在回归直线上求解相关参数的值；二是回归直线方程的应用，利用回归直线方程求出的数值应是一个估计值，不是真实值．经典例题：下图是某地区 2000 年至 2016 年环境基础设施投资额（单位：亿元）的折线图．为了预测该地区 2018 年的环境基础设施投资额，建立了与时间变量的两个线性回归模型．根据 2000 年至 2016 年的数据（时间变量的值依次为 1,2.，⋯⋯ 17 ）建立模型①： y=-30.4+13.5t ；根据 2010 年至 2016 年的数据（时间变量的值依次为）建立模型②： y=99+17.5t ．（ 1）分别利用这两个模型，求该地区 2018 年的环境基础设施投资额的预测值；（2）你认为用哪个模型得到的预测值更可靠？并说明理由．思路分析：（ 1）两个回归直线方程中无参数，所以分别求自变量为 2018 时所对应的函数值，就得结果，（ 2）根据折线图知 2000 到 2009 ，与 2010 到 2016 是两个有明显区别的直线，且 2010 到 2016 的增幅明显高于 2000 到 2009 ，也高于模型 1 的增幅，因此所以用模型 2 更能较好得到 2018 的预测.解析：（ 1）利用模型①，该地区 2018 年的环境基础设施投资额的预测值为= –30.4+13.5 ×19=226.1 （亿元）．利用模型②，该地区 2018 年的环境基础设施投资额的预测值为 =99+17.5×9=256.5 （亿元）（2）利用模型②得到的预测值更可靠．理由如下：（ i）从折线图可以看出， 2000 年至 2016 年的数据对应的点没有随机散布在直线y= –30.4+13.5t 上下，这说明利用 2000 年至 2016 年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势． 2010 年相对 2009 年的环境基础设施投资额有明显增加， 2010 年至 2016 年的数据对应的点位于一条直线的附近，这说明从 2010 年开始环境基础设施投资额的变化规律呈线性增长趋势，利用2010 年至 2016 年的数据建立的线性模型 =99+17.5t 可以较好地描述 2010 年以后的环境基础设施投资额的变化趋势，因此利用模型②得到的预测值更可靠．（ ii）从计算结果看，相对于 2016 年的环境基础设施投资额 220 亿元，由模型①得到的预测值 226.1 亿元的增幅明显偏低，而利用模型②得到的预测值的增幅比较合理，说明利用模型②得到的预测值更可靠．以上给出了 2 种理由，考生答出其中任意一种或其他合理理由均可得分．总结：若已知回归直线方程，则可以直接将数值代入求得特定要求下的预测值；若回归直线方程有待定参数，则根据回归直线方程恒过中心点求参数 .线性回归方程是利用数理统计中的回归分析，来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法之一，线性回归也是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。

回归方程式
回归方程公式：b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)。

1、回归直线方程可以用最小二乘法求回归直线方程中的a,b，从而得到回归直线方程。

线性回归也是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。

按自变量个数可分为一元线性回归分析方程和多元线性回归分析方程。

2、回归方程是对变量之间统计关系进行定量描述的一种数学表达式。

线性回归模型，是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。

其表达形式为y = w'x+e，e为误差服从均值为0的正态分布。

3、最小二乘法又称最小平方法，是一种数学优化技术。

与最小二乘法不同的是，最大似然法需要已知这个概率分布函数，这在实践中是很困难的。

一般假设其满足正态分布函数的特性，在这种情况下，最大似然估计和最小二乘估计相同。