重量及重心坐标的求法

灰度重心法公式摘要：一、灰度重心法简介1.灰度重心法的概念2.灰度重心法的应用场景二、灰度重心法公式推导1.灰度值与重量的关系2.灰度重心坐标公式三、灰度重心法计算过程1.图像预处理2.计算灰度值与重量3.计算灰度重心坐标四、灰度重心法的优缺点1.优点2.缺点五、灰度重心法在图像处理中的应用1.图像二值化2.图像分割正文：灰度重心法是一种计算图像灰度重心的方法，它通过计算图像中每个像素点的灰度值与对应权重，从而得到图像的灰度重心坐标。

灰度重心法广泛应用于图像处理领域，例如图像二值化、图像分割等。

灰度重心法的公式推导如下：1.灰度值与重量的关系：对于图像中的每个像素点（x, y），其灰度值为I(x, y)，权重为W(x, y)。

灰度值与重量之间的关系可以表示为：I(x, y) = k * W(x, y)，其中k为常数。

2.灰度重心坐标公式：设图像的宽为W，高为H。

图像的灰度重心坐标（μx，μy）可以通过以下公式计算：μx = ∑(x * I(x, y)) / ∑I(x, y)μy = ∑(y * I(x, y)) / ∑I(x, y)其中，∑表示对图像中所有像素点进行求和。

灰度重心法计算过程如下：1.图像预处理：对输入图像进行灰度化处理，即将RGB图像转换为灰度图像。

2.计算灰度值与重量：根据预处理后的图像，计算每个像素点的灰度值I(x, y)和权重W(x, y)。

灰度值与重量的关系如上所述。

3.计算灰度重心坐标：根据灰度值与重量，使用上述公式计算灰度重心坐标（μx，μy）。

灰度重心法具有简单、易于实现的优点，适用于计算灰度分布较为均匀的图像重心。

然而，当图像中存在边缘、纹理等复杂特征时，灰度重心法的计算结果可能不准确。

因此，灰度重心法在实际应用中有一定的局限性。

灰度重心法在图像处理领域具有广泛的应用，例如：1.图像二值化：通过计算图像的灰度重心，可以将图像分为两部分，从而实现图像的二值化。

2.图像分割：在目标检测、识别等任务中，灰度重心法可以用于计算目标的质心，从而辅助进行图像分割。

话题1：重心与质心的确定一、平行力的合成与分解物体所受的几个力的作用线彼此平行，且不作用于一点，即为平行力（系）。

在平行力的合成或分解的过程中，必须同时考虑到力的平动效果和转动效果，后者要求合力和分力相对任何一个转轴的力矩都相同。

两个同向平行力的合力其方向与两个分力方向相同，其大小等于分力大小之和。

其作用线在两个分力作用点的连线上。

合力作用点到分力作用点的距离与分力的大小成反比。

例如：两个同向平行力A F 和B F ，其合力的大小A B F F F =+，合力作用点O 满足A B AO F BO F ⋅=⋅的关系。

两个反向平行力的合力其方向与较大的分力方向相同，其大小等于分力大小之差。

其作用线在两个分力作用点的连线的延长线上，且在较大的分力的外侧。

合力作用点到分力作用点的距离与分力的大小成反比。

例如：两个反向平行力A F 和B F 的合成其合力的大小B A F F F =-(假如B A F F >，则F 和B F 同向)其合力的作用点满足A B AO F BO F ⋅=⋅的关系。

一个力分解成两个平行力，是平行力合成的逆过程。

二、重心和质心重心是重力的作用点。

质心是物体(或由多个物体组成的系统)质量分布的中心。

物体的重心和质心是两个不同的概念，当物体远离地球而不受重力作用时，重心这个概念就失去意义，但质心却依然存在。

对于地球上体积不太大的物体，由于重力与质量成正比，重心与质心的位置是重合的。

但当物体的高度和地球半径比较不能忽略时，两者就不重合了，如高山的重心比质心要低一些。

在重力加速度g 为常矢量的区域，物体的重心是惟一的（我们讨论的都是这种情形），BF AF FO BA BF AF F OBA重心也就是物体各部分所受重力的合力的作用点，由于重力与质量成正比，重力合力的作用点即为质心，即重心与质心重合。

求重心，也就是求一组平行力的合力作用点。

相距L ，质量分别为12,m m 的两个质点构成的质点组，其重心在两质点的连线上，且与12,m m 相距分别为1L ,2L ：1122m L m L = 12L L L +=2112m LL m m =+1212m LL m m =+均匀规则形状的物体，其重心在它的几何中心，求一般物体的重心，常用的方法是将物体分割成若干个重心容易确定的部分后，再用求同向平行力合力的方法找出其重心。

船舶总纵强度计算一.主要数据及原始资料1.主要数据计算船长L=94.407m船宽B=17.000m水密度ρ=1.000t/m3重力加速度g=9.8m/s2计算状态满载到港2.根据完整稳定性计算书选取初始计算参数总重量W=66756.7768 kN重心纵向坐标Xg=-5.121m计算吃水吃水dm=4.956m3.确定总重量后，根据静水力曲线数据及线性插值得到浮心纵向坐标Xb=0.6721m浮心垂向坐标Zb=2.5967m漂心纵向坐标Xf=2.8279m水线面面积Aw=1500.5605m2纵稳心半径R=146.5132m二.重量分布计算1.用库尔求莫夫法计算空船重量分布船舶集度系数K取42.其它重量分布确定根据完整稳定性计算书中船总重量分布及总布置图粗略确定各部分重量分部。

3.总重量分部确定将各站重量加和，得到总重量分部曲线。

三.浮力分布计算1.第一次近水计算首吃水mxLRxxddfbgmf0875.5)2(1=--+=尾吃水mxLRxxddfbgma394.84)2(1=+--=浮力B1=66261.1192KN浮心纵向坐标Xb1=0.9757M精度检验（W-B1)/W=0.74%（Xg-Xb1）/L=0.09% 2.第二次近水计算首吃水5.1493)2(1112=--+⋅⋅-+=fbgffxLRxxagBWddρ尾吃水482.84)2(1112=+--⋅⋅-+=fbgaaxLRxxagBWddρ浮力B1= 66749.1041 KN浮心纵向坐标Xb1= 1.0258 M精度检验（W-B1)/W=0.01%（Xg-Xb1）/L=0.03% 满足精度要求。

3.计算各理论站浮力四.静水剪力与弯矩计算根据浮力分部和重力分部计算船舶荷载、剪力、弯矩，得到剪力分布和弯矩分部。

五. 静波浪剪力Nw 和弯矩Mw 计算1. 计算坦谷波波形（选择中拱状态）波长λ=L=94.407m 波高h= λ/30+2=5.15m坦谷波垂向坐标值采用余弦级数展开式计算，即)4cos 1(2cos y 2B x x λπλπτλπτ-+=得到坦谷波波线图。

直角三角形重心知识点总结一、重心的概念重心是一个几何形状的质心，表征着这个形状的整体重量的几何中心。

在直角三角形中，三条中线的交点就是重心，位于三角形的内部。

重心是一个三角形的重要性质，能够帮助我们研究三角形的性质和相关定理。

二、重心的性质1. 重心将三角形分成三个面积相等的三角形2. 重心到顶点的距离是中线到所在边中点距离的二分之一3. 重心到对边中点的距离是重心到这条边的距离的二分之一4. 重心到任一顶点的距离是重心到非对角顶点中点的距离的二分之一5. 重心同时在三条中线上三、如何求直角三角形的重心通常我们可以通过以下几种方法来求解直角三角形的重心：1. 根据重心的定义来求解2. 利用中线长度关系来求解3. 利用坐标方法来求解下面我们就分别来看一下这几种方法的具体步骤。

四、根据重心的定义来求解在直角三角形中，重心就是三条中线的交点，所以我们可以通过以下步骤来求解：1. 先找到直角三角形的三个顶点A、B、C2. 根据中位线的定义，找到AB、BC、AC的中点D、E、F3. 用直线相交的方法求解出重心G这种方法简单直接，但是需要保证我们能够准确地找到中点和重心的坐标。

五、利用中线长度关系来求解在直角三角形中，三条中线的长度关系是：AG^2 = 2 * BG^2 = 2 * CG^2。

我们可以通过这个关系来求解重心。

具体步骤如下：1. 先找到直角三角形的三个顶点A、B、C2. 根据中位线长度关系，求解出重心G的坐标这种方法相对简单，只需要比较中线长度关系即可求解出重心的坐标。

六、利用坐标方法来求解在直角三角形中，我们可以利用坐标方法来求解重心的坐标。

具体步骤如下：1. 已知直角三角形的三个顶点A、B、C的坐标2. 分别求得AB、BC、AC的中点D、E、F的坐标3. 利用中点和重心的关系，求解出重心G的坐标这种方法是最直接的，只需要根据坐标计算的方法，即可求解出重心的坐标。

七、直角三角形重心的应用1. 利用重心来求解三角形的面积直角三角形的重心可以将三角形分成三个面积相等的三角形，利用这一性质，我们可以通过重心来求解三角形的面积。

你听过四边形的重心吗你听过四边形的重心吗你听过四边形的重心吗你听过四边形的重心吗重心的探讨重心的探讨重心的探讨重心的探讨p1 物理课本对n个点的重心质量中心作如下的定义1直线坐标系上n个点的坐标分别为iiAx1in且点iiAx的质量为1imin 定义这n个点的质量中心为x其中1nxmkkMkx∑i其中1nkkMm∑ 2平面坐标系上n个点的坐标分别为iiiAxy1in且点iiiAxy的质量为1imin 定义这n个点的质量中心为xy其中11nnx mymkkkkMMkkxy∑∑ii其中1nkkMm∑ 3空间坐标系上n个点的坐标分别为iiiiAxyz1in且点iiiiAxyz的质量为1imin 定义这n个点的质量中心为xyz其中111kkkkkknnnxmymzmMMMkkkxyz∑∑∑iii其中1nkkMm∑ 单元一单元一单元一单元一nnnn个均匀点的重心个均匀点的重心个均匀点的重心个均匀点的重心数学课假设每个点的质量均相同平面坐标系上n个点的坐标分别为iiiAxy1in 且点iiiAxy的质量为m常数定义这n个点的重心为xy 11nkkkkxnx mMnkx∑∑in个点之x坐标的平均11nkkkkynymMnky∑∑in个点之y坐标的平均其中11nnkkkMmmnm∑∑i 例题一111222AxyAxy为平面坐标系上的两点1试求其重心G的坐标答根据重心定义得121222xxyyGxy 2试说明重心G就是12AA的中点。

答easy 3试证120GAGA pfG是12AA的中点??12GAGA120GAGA 定理一M为AB的中点W为任意点试证2WAWBWM pfM为AB的中点??AMMB即0MAMB ??2202WAWBWMMAWMMBWMMAMBWMWM 例题二111222333AxyAxyAxy为平面坐标系上的三点1试求其重心G的坐标答根据重心定义得12312333xxxyyyGxy 2试证1230GAGAGA pf令O为原点则1230GAGAGA1230GOOAGOOAGOOA??11231231233303GOOAOAOAGOAOAOAGOAOAOA 12312333xxxyyyGxy?? 3问G点在那裏由上面的定理一122GAGAGM其中M为12AA的中点123302GAGAGAGAGM 你听过四边形的重心吗重心的探讨p2 ??3AGM共线且G在3AM之间且3:2:1GAGM ??G在中线3AM上且3:2:1GAGM同理可证G在另二条中线上。

3.1仓库选址3.1.1 重心法求最佳仓库选址的原理重心法是根据几何的方法确定在一个平面或空间内分布有若干的点，求出一点到这若干的点的总距离最短。

重心法是一种模拟方法，它将物流系统中的需求点和资源点看成是分布在某一平面范围内的物流系统，各点的需求量和资源量分别看成是物体的重量，物体系统的重心作为物流网点的最佳设置点，利用求物体系统重心的方法来确定物流网点的位置。

通常重心法可以用于解决仓库的选址、配送中心的选址等问题。

重心法在解决配送中心的选址问题时，它把运输成本看成现有配送点之间的运输距离和运输的货物量的线性函数。

重心法首先要在坐标系中标出各个地点的位置，目的在于确定各点的相对距离。

坐标系采用经度和纬度建立坐标。

这样就确定了各个配送点的具体地理位置。

同时考虑各段运输路线的运输成本。

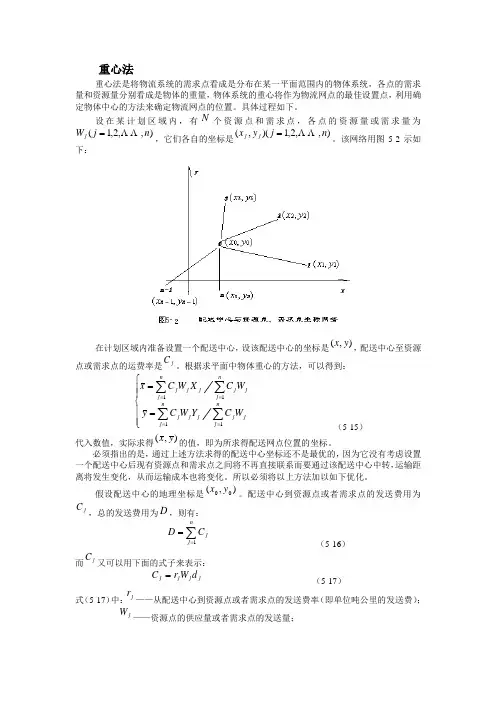
设拟建的配送中心有N 个需要收件的配送点，它们所在的位置坐标为(i i y x ,)，其中i=1,2，···n ，拟建的配送中心的坐标为(x,y),如下图所示：Y根据在中国地图上查找各城市的经纬度得到每个城市的地理坐标（保留小数点后货物从i 地运至配送中心所在地的运输费用是i c ，设i h 为运输费率即单位货物运输单位距离的费用，且假设配送点与配送中心所在地之间的道路为直线，距离为i d ，i w 为运输量。

则i i i i d w h c ⨯⨯=...........................(1) 且i d =22)()(i i y y x x -+- (2)总运输费用H 为： H=i i ni i ni i d w h c ⨯⨯=∑∑==11 (3)由于i d 与配送中心位置(x,y)有关，因此总运输费用是x,y 的函数，将式(2)带入式(3),得：221)()(),(i i i ni i y y x x w h y x H -+-⨯⨯=∑= (4)（1）根据以上公式和案例给定的各个分拨中心的业务量求出配送中心的初始地理坐标（假设一级分拨中心的运输费率为0.05，二级分拨中心的运输费率为0.075）初始坐标：X=111.25585/3.67=30.3149 Y=442.185525/3.67=120.49 （2）计算配送中心在目前初始坐标位置的总运输成本则配送中心在初始坐标的总费用H=3.927671108为求得运输费用最小的配送中心，就变成了对函数H(x,y)求极值的问题，即求(**,y x ),使：H=H(**,y x )min根据函数极值的原理，式(4)分别对x,y 求偏导，令偏导为0，得：0/)(1=-=∂∂∑=i i i ni i d x x w h x H………………………(5) 0/)(1=-=∂∂∑=i i i n i i d y y w h y H………………………(6) 由式(5)和(6)可以求得函数H(x,y)的极值点，由于式(6)是非线性方程组，难以求得**,y x 的表达式，需要用迭代法求解，展开式(5)和(6)得：∑∑===ni iii ni iiiid wh d xw h x 11*// (7)∑∑===ni iii ni iiiid wh d yw h y 11*// (8)（3）求出第一次迭代以后的配送中心的坐标X=189.3623755/6.251962728=30.2884684Y=753.9872233/6.251962728=120.6000829则第一次迭代以后的坐标为（30.2884684，120.6000829）（4）计算配送中心在目前初始坐标位置的总运输成本则配送中心在初始坐标的总费用H=3.860409954其中i d =2*2*)()(i i y y x x -+- ，将式(7)和(8)写成迭代式，有k 次迭代结果表达式：()()∑∑=-=-=ni k i ii ni k i iiid wh d xw h k x 1111*//)( (9)()()∑∑=-=-=ni k i iini k i iiid wh d yw h k y 1111*//)( (10)其中：()2*)1(2*)1(1)()(i k i k k i y y x x d -+-=--- (11)如果k H <1-k H ,说明总运费仍有改进改善的余地，返回步骤(5),继续叠加；否则，说明(()()*1*1,--k k y x )为最佳场址，则停止叠加。

轻型飞机重量重心的测量及计算方法研究刘福佳;顾超【摘要】飞机重量重心测量是为了验证飞机理论重量重心的准确性,是飞机总装完成后和使用过程中维修前后的必要环节.根据飞机重量重心测量原理,结合轻型飞机的设计特点和使用要求,给出了适合轻型飞机的称重目的、称重状态要求、称重技术要求、称重设备要求;并给出了轻型飞机重量及重心的测量方法;最后推导出了轻型飞机重量及重心的计算公式.为轻型飞机在生产阶段重量及重心的测量与计算提供一种简单的操作方法及计算公式,保证实际测量飞机重量及重心位置的准确性.【期刊名称】《沈阳航空航天大学学报》【年(卷),期】2018(035)002【总页数】5页(P17-21)【关键词】轻型飞机;重量和重心;称重要求;测量方法;计算公式【作者】刘福佳;顾超【作者单位】辽宁通用航空研究院设计部,沈阳110136;辽宁通用航空研究院设计部,沈阳110136【正文语种】中文【中图分类】V221+.5飞机重量重心的变化影响飞机、机动、起降等性能，直接影响飞机的安全性[1-4]。

飞机的重量重心贯穿了整个飞机的研制阶段，在生产阶段需要实际测量飞机的重量和重心[5-8]，而采用的测量方法的好坏也最终决定了实际测量数据的准确性和可靠性。

本文根据《飞机设计手册》第8册[3]提供的飞机重量和重心测量原理，并结合轻型飞机的设计及使用特点，给出了轻型飞机重量和重心的测量要求、测量方法和计算方法，以确定轻型飞机实际重量和重心，为检验轻型飞机重量和重心理论值与实际值的符合性提供一种准确有效的方法。

1 轻型飞机称重及重心测量目的及要求1.1 轻型飞机称重的目的(1)确定飞机的实际重量和重心位置；(2)检验飞机重量、重心理论值与实际值的符合性；(3)根据特定的飞行要求配置所需的飞机重心[9-13]。

1.2 轻型飞机称重状态要求(1)空机状态，按“基本空机重量”状态配套齐全的飞机。

民用飞机依据CCAR-23部或CCAR-25部的规定；(2)特定状态，根据有关配套文件的规定。

“重量”的定义关于重量，可以这样说，人们对重量的熟悉程度要强于对质量的熟悉程度．但长期以来，由于重量的定义也具有多种表述，结果在物理学等方面，使重量这个概念变得含混不清．综观现行的物理教材和参考书，关于重量的定义亦有多种表述．第一种为：“重量是一种力，它是由地球吸引而产生的，是使物体产生重力加速度的原因．”第二种为：“重量就是重力．”第三种为：“重量是物体对水平支持物的压力或物体对竖直悬挂绳子的拉力．”第四种为：“重量就是重力的大小．”以上重量的第一、第二、第三种表述都给重量赋予了力的含义．但第一、第二种表述说明重量的力性属万有引力，而第三种表述说明重量的力性属弹性力；重量的第四种表述扬弃了重量的力性，它既保留了重量和重力的数量关系，又克服了重量作为一种力所带来的缺陷和麻烦（指与引力、重力相混淆）．重量既然作为重力的量度，就能用弹簧秤直接来测得物体所受的重力大小．物体重量的多种定义，哪一种好些？这问题历来是有争论的．但是，由于定义本来是人为的，是为了便于解释问题而指出的，重要的是，若采用某一种表述作定义，那么，有关的现象就应当用这个定义所规定的含义去解释，不能前后矛盾．现行中学物理采用“重量就是重力”的定义，尽管如此，但是习惯上只说“重力的分解”，而不说“重量的分解”；只说“物体有重量”，而不说“物体有重力”；只说“重力加速度”而不说“重量加速度”．从以上重量定义的多种表述可以看出，重量仅在物理学上就已含有多重意义了，若考虑到重量一词在日常生活中的运用，其含义就更多了．譬如，日常生活中，我们购买粮食、水果等物品时，常说它们的重量是多少克或多少公斤，这里说的重量实际上是质量．因为售货员使用的台秤或杆秤，跟天平一样，都属于杠杆类量具，只能测量物体的质量．另外，公斤和克都是质量的单位．重量术语的多重意义，给教学、科研、图书出版以及国际交往等带来很多不便．事实上，质量、万有引力、重力及物体作用在支撑物上的力，各自都有明确的定义和名称．直接利用这些概念完全可以很好地分析和解决有关问题．在此情形下，保留“重量”概念已无实际意义．国际计量大会早就建议在科学术语中取消重量一词，而把日常生活中的重量看作是质量的别名．世界上已有80多个国家接受国际计量大会的建议．国际计量大会已在近年通过规定，重量这一名称，今后不再具有力的含义，重量是质量的别名．1984年4月27日国务院发布的《中华人民共和国法定计量单位使用方法》也接受国际计量大会通过的上述规定．今后凡在指力的场合，“重量”应改成“重力”．在科学技术领域中最好不采用“重量”一词．当然，在日常生活中仍可采用“重量”一词，但注意，它只是“质量”一词的同义词．弹力选自《中学教学实用全书》直接接触的物体间因发生弹性形变而产生的相互作用力，或发生弹性形变物体内部相邻两部分间产生的相互作用力，称为弹力．弹力的产生以物体发生弹性形变为先决条件，因而不可认为相互接触的物体间一定存在弹力作用．从本质上讲，弹力起源于物质内部带电的或具有磁矩的微粒间的电磁力．弹力的大小和方向是由物体的形变来决定的．在弹性限度内，弹力的大小与形变的大小成正比．弹力的方向与形变的方向相反．弹力是一种被动力．分析相互接触的物体间是否存在弹力时，要根据物体受到其它力作用的情况及物体的运动状态来加以确定．对于发生弹性形变物体内部的弹力，通常把相邻两部分间每单位截面积上的弹力称为应力．其中与截面垂直的应力称为正应力，而与截面相切的应力称为切应力．在国际单位制中，应力的单位是2m /N ． 重力选自《中学教学实用全书》处于地面附近的物体，主要受到的是地球的万有引力，因而把地球对物体的万有引力称为重力．方向指向地心．严格地讲还应考虑到地球自转这一因素，从作用效果上把地球对物体的万有引力F 等效成两个分力1F 和2F 看待（如图所示），其中分力1F 提供了物体随地球自转的力，而把另一分力2F 称为重力，方向竖直向下．把重力视为物体由于地球的吸引而受到的力看待时，重力和万有引力是有区别的．由于地球并非理想球体，物体处在不同纬度上随地球自转所需的向心力不同，以及地球的密度分布不均匀等因素，物体受到的重力（及重力加速度）是随纬度变化的．同一物体在赤道的重力最小，在两极的重力最大．把重力视为地球对物体的万有引力看待时，物体受到的重力（及重力加速度）要随距地面的高度变化．从广义上讲，在宇宙空间的星体表面的物体都要受到由星体的引力而产生的重力作用．重力的定义重力是力学中最重要、最基本的概念之一．但是，国内外各种课本及参考书对重力概念的定义不尽一致，目前对重力的定义大致有以下三类．第一类定义：“地球对物体的引力称重力”．“重力就是由于地球吸引而使物体受到的力”．第二类定义：“地球对其附近物体吸引的力是重力”．“地球对地球表面附近物体的引力称重力”．第三类定义：“质点以线悬挂并相对于地球静止时，质点所受重力的方向沿悬线且竖直向下，其大小在数值上等于质点对悬线的拉力”．“实际上，重力就是悬线对质点拉力的平衡力”．“物体在地球表面附近自由下落时，有一竖直方向的重力加速度g ，产生此重力加速度的力称为重力”．第一类定义很明确，重力就是指地球对物体的万有引力．重力即是力，就是矢量，其方向就是地球对物体引力的方向，即指向地球中心．按这类定义，重力就成了引力的同义词．其实，这类定义只有在不考虑地球自转所引起的效果时才有意义．第二类定义的共同特点是有“表面”、“附近”此类限制性词．这些“表面”、“附近”表达着怎样的意思呢？如只是一个区域性概念的话，那就是说只有地球表面附近的引力才称重力，除此以外，就只称引力，不再称重力了；另外，到底距地球表面多远才不算“表面”、“附近”呢？可见，第二类重力定义给读者的概念是模糊的、不确切的．第三类定义分别从静力学形式和动力学形式给出了重力的“操作性定义”，并暗示了重力不是纯地球引力，而是把地球自转影响考虑在内的地球引力和物体随地球绕地轴转动所受的向心力之差．这类定义美中不足的是未能明确表达出重力的主要本质，即“地球引力”这一本质因素．综上所述，以上三类关于重力的定义都不够确切．重力的比较确切的定义是：“随地球一起转动的物体，所表现出的、所受地球的引力，称物体的重力．”根据这种定义，重力概念的内涵有：（1）重力的本质来源是地球的引力．（2）重力是一个表观的概念，是物体随地球一起转动时受到地球的引力．（3）重力等于物体受地球的引力和随地球绕轴转动所需向心力的矢量差．为了能对重力的大小、方向有一个较直观、明确的认识，下面以地球表面的物体为例加以说明．设地球是均匀球体，其自转角速度为ω，则处于地球上P 点的物体受到地球的引力为F ，随地球自转所需的向心力为f ，f 是F 的一个分力．根据我们关于重力的定义，F 的另一个分力G 就是物体的重力（见图）．从图示可见，物体重力G 确是引力F 与向心力f 的矢量差，其方向一般并不指向地球中心，而偏离一个小角度θ，指向平常所说的竖直方向．平常我们所说物体的自由落体加速度，就是在重力的作用下产生的，所以，这加速度又称重力加速度，方向当然也不严格指向地心．至于重力的大小，一方面可用弹簧秤测定，另一方面可根据图示计算得：ϕω2220cos R m RMm G G -== 式中R 是地球半径，ϕ为物体所在处的纬度，M 为地球质量，m 为物体质量，0G 为引力常数．由上式可看出，在赤道处，0=ϕ，G 最小，与20R Mm G 相差的百分比约为3105.3-⨯；在两极处，20RMm G G =，G 最大；在其他纬度处，G 介于两者之间．重心选自《中学教学实用全书》处于地面附近重力场中的物体，若比地球小得多，物体各部分受到的重力可看作是连续分布的平行力，这些平行力的合力作用点称为重心．重心的位置与物体的形状及质量分布情况有关．形状规则、质量分布均匀的物体，重心位于它的几何中心处．某些形状不规则物体的重心，可以通过实验的方法测定其位置．例如，薄板状物体的重心，可采用悬挂法测定．物体的重心可以在它的内部，也可以在它的外部．重心和质心重心是重力的作用点．质心是物体（或由多个物体组成的系统）质量分布的中心．质心是一个非常重要的概念，在今后的学习中我们会发现，运用质心的一些性质进行解题有时会给我们带来很大的方便．物体的重心和质心是两个不同的概念，当物体远离地球而不受重力作用时，重心这个概念就失去意义，但质心却依然存在．对于地球上体积不太大的物体．重心与质心的位置是重合的．但当物体的高度和球半径比较不能忽略时，两者就不重合了，如高山的重心比质心要低一些．求重心的常用方法有分隔法（含负质量法）和坐标法．如图所示的棒锤，假设匀质球A质量为M、半径为R；匀质棒B质量为m、长度为l．求它的重心．第一种方法是将它分隔成球和棒两部分，然后用同向平行力合成的方法找出其重心C．C在AB连线上，且mBCMAC⋅=⋅（如图）．第二种方法是将棒锤看成一个对称的“哑铃”和一个质量为－M的球A'的合成（如图），用反向平行力合成的方法找出其重心C，C在AB连线上，且MCAmMBC⋅'=+⋅)2(．不难看出两种方法的结果都是：mMlRMBC+⎪⎭⎫⎝⎛+=2．根据质心的定义，我们还可用坐标法求物体系的质心．如果物体系的总质量为M，且其各部分的质心分布在同一平面内．在此平面内任取一点为原点建立平面直角坐标系．用im 和),(iiyx表示此物体系中第i个部分的质量和质心位置坐标，则此物体系的质心在坐标平面内的坐标为⎪⎪⎩⎪⎪⎨⎧==∑∑MymyMxmxiiciic如上面的例子，以B点为原点，水平向右为x轴正方向，则A、B的合质心的位置为⎪⎪⎩⎪⎪⎨⎧+⋅+⋅=+⋅+⎪⎭⎫ ⎝⎛--⋅=m M m M y m M m l R M x c c 0002 即：⎪⎪⎩⎪⎪⎨⎧=+⎪⎭⎫ ⎝⎛+⋅=02c c y m M l R M x 负号表示质心的位置在B 点左侧（如图）．用坐标法求物体的重心是比较方便的．坐标法与分隔法一样，都是平行力的合成方法推导出来的，有兴趣的读者可以尝试推导一下．力的分类中学阶段提到的力可以分成接触力和非接触力两类，接触力又分为弹力、摩擦力． 弹力是由于物体发生弹性形变产生的力．推、拉、提、压等形式中产生的力都是弹力．摩擦力则是物体发生相对运动或相对运动趋势时，在物体接触面间发生的力．非接触力，课本中提到的有重力、电力、磁力，它们又可归为场力，是场与某些物体间发生的力，现代物理学研究中则把它分为强相互作用与弱相互作用．根据现代科学研究的成果，按力的基本性质区分，自然界中当前所认识的各种力可归结为下列四种基本相互作用：（1）引力相互作用——由于物体具有质量，物体之间有万有引力相互作用．（2）电磁相互作用——存在于静止电荷或运动电荷之间的相互作用．（3）强相互作用——存在于核子（中子和质子）、介子和超子之间的一种相互作用．（4）弱相互作用——存在于基本粒子之间的另一种相互作用，主要存在于粒子的衰变过程中．后面两种相互作用，都是基本粒子之间的近距作用，人们在20世纪之前并不知道．对于宏观物体之间的相互作用，重要的是前两种．。

重心法重心法是将物流系统的需求点看成是分布在某一平面范围内的物体系统，各点的需求量和资源量分别看成是物体的重量，物体系统的重心将作为物流网点的最佳设置点，利用确定物体中心的方法来确定物流网点的位置。

具体过程如下。

设在某计划区域内，有N 个资源点和需求点，各点的资源量或需求量为),,2,1(n j W j =，它们各自的坐标是),,2,1)(,(n j y x j j =。

该网络用图5-2示如下：在计划区域内准备设置一个配送中心，设该配送中心的坐标是),(y x ，配送中心至资源点或需求点的运费率是jC 。

根据求平面中物体重心的方法，可以得到：⎪⎪⎩⎪⎪⎨⎧==∑∑∑∑====n j nj j j j j j n j nj j j j j j W C Y W C y W C X W C x 1111 （5-15）代入数值，实际求得),(y x 的值，即为所求得配送网点位置的坐标。

必须指出的是，通过上述方法求得的配送中心坐标还不是最优的，因为它没有考虑设置一个配送中心后现有资源点和需求点之间将不再直接联系而要通过该配送中心中转，运输距离将发生变化，从而运输成本也将变化。

所以必须将以上方法加以如下优化。

假设配送中心的地理坐标是),(00y x 。

配送中心到资源点或者需求点的发送费用为jC ，总的发送费用为D ，则有：∑==nj jC D 1（5-16）而jC 又可以用下面的式子来表示：jj j j d W r C = （5-17）式（5-17）中：j r——从配送中心到资源点或者需求点的发送费率（即单位吨公里的发送费）；jW ——资源点的供应量或者需求点的发送量；jd ——从配送中心到资源点或者需求点的直线距离。

其中，jd 也可以写成如下形式：][)(2)(2021j jj y yx x d --=- （5-18）把方程式（5-18）代入（5-17），得到：∑==nj jj j d W r D 1（5-19）从方程式（5-19）和方程式（5-16）可以求得使D 为最小的),(00y x 。