光的衍射一
- 格式:ppt
- 大小:272.50 KB
- 文档页数:11





第7章 光的衍射一、选择题 1(D ),2(B),3(D ),4(B),5(D),6(B),7(D),8(B),9(D ),10(B ) 二、填空题(1). 1.2mm ,3.6mm (2). 2, 4 (3). N 2,N(4). 0,±1,±3,.。
.。
.。
(5). 5 (6). 更窄更亮 (7). 0.025(8). 照射光波长,圆孔的直径 (9). 2。
24×10-4 (10). 13.9 三、计算题1. 在某个单缝衍射实验中,光源发出的光含有两种波长λ1和λ2,垂直入射于单缝上.假如λ1的第一级衍射极小与λ2的第二级衍射极小相重合,试问 (1) 这两种波长之间有何关系?(2) 在这两种波长的光所形成的衍射图样中,是否还有其他极小相重合?解:(1) 由单缝衍射暗纹公式得111sin λθ=a 222sin λθ=a 由题意可知 21θθ= , 21sin sin θθ=代入上式可得212λλ=(2) 211112sin λλθk k a == (k 1 = 1, 2, ……) a k /2sin 211λθ=222sin λθk a = (k 2 = 1, 2, ……) a k /sin 222λθ=若k 2 = 2k 1,则θ1 = θ2,即λ1的任一k 1级极小都有λ2的2k 1级极小与之重合.2. 波长为600 nm (1 nm=10-9 m)的单色光垂直入射到宽度为a =0。
10 mm 的单缝上,观察夫琅禾费衍射图样,透镜焦距f =1。
0 m ,屏在透镜的焦平面处.求: (1) 中央衍射明条纹的宽度∆ x 0;(2) 第二级暗纹离透镜焦点的距离x 2 解:(1) 对于第一级暗纹,有a sin ϕ 1≈λ因ϕ 1很小,故 tg ϕ 1≈sin ϕ 1 = λ / a故中央明纹宽度 ∆x 0 = 2f tg ϕ 1=2f λ / a = 1.2 cm(2) 对于第二级暗纹, 有 a sin ϕ 2≈2λx 2 = f tg ϕ 2≈f sin ϕ 2 =2f λ / a = 1.2 cm3. 如图所示,设波长为λ的平面波沿与单缝平面法线成θ向入射,单缝AB 的宽度为a 小值(即各暗条纹)的衍射角ϕ.解:1、2两光线的光程差,在如图情况下为ϕθδsin sin a a BD CA -=-=由单缝衍射极小值条件 a (sin θ -sin ϕ ) = ± k λ k = 1,2,……得 ϕ = sin —1( ± k λ / a+sin θ ) k = 1,2,……(k ≠ 0)4。
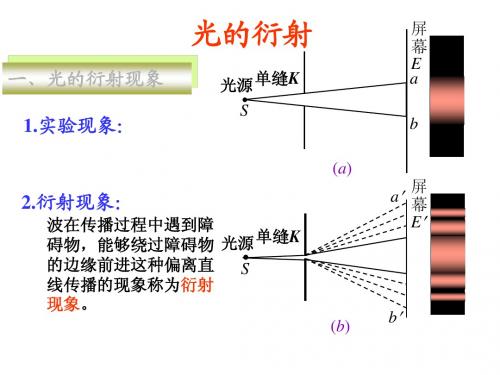
光的衍射单缝和双缝衍射光的衍射是光学中一个重要的现象,它揭示了光的波动性质。
在衍射现象中,光线经过一个障碍物或孔径后发生偏折,从而产生明暗的交替条纹。
在实际应用中,单缝和双缝衍射是常见的研究对象。
本文将对光的衍射,特别是单缝和双缝衍射进行探讨。
一、光的衍射概述光的衍射是指光通过物体的缝隙或者物体的边缘时发生偏折现象,并产生特定的干涉图样。
这种现象直接揭示了光的波动性质,是波动光学的重要内容。
二、单缝衍射原理及特点单缝衍射是指光通过一个非常细小的缝隙时发生的衍射现象。
它的原理可以用赫亚(Huygens)原理来解释。
根据赫亚原理,光波在传播过程中,每个点都可以看做是次波源,产生的新次波在各个方向上形成球面,当这些球面相互叠加时,形成了最终的衍射图样。
单缝衍射产生的主要特点包括:1. 衍射图样由中央的亮纹和两侧的暗纹构成,衍射角度较小,纹理较宽。
2. 亮纹的中央亮度最大,逐渐向两侧递减,直至变为暗纹。
3. 亮纹和暗纹的宽度与缝宽有关,缝宽越窄,亮纹和暗纹越窄。
4. 亮纹和暗纹的间距与波长有关,波长越短,间距越大。
三、双缝衍射原理及特点双缝衍射是指光通过两个平行的缝隙时产生的衍射现象。
它是由于两个缝隙同时成为光波的波前源,产生了一定的干涉现象。
双缝衍射的主要特点包括:1. 衍射图样由一组亮纹和暗纹构成,呈现出明暗相间的条纹。
2. 在中央的亮纹位置,两个波峰叠加形成增强,形成很亮的亮纹;在中央的暗纹位置,两个波峰和波谷相互抵消,形成较暗的暗纹。
3. 亮纹和暗纹的宽度与缝宽、波长有关,缝宽越窄,亮纹和暗纹越窄;波长越短,亮纹和暗纹越窄。
4. 亮纹和暗纹的间距与波长、缝间距有关,波长越短,间距越大;缝间距越大,间距越小。
四、单缝和双缝衍射的应用光的衍射在实际应用中有重要的作用,尤其是单缝和双缝衍射的研究和应用更加广泛。
在物理实验中,单缝衍射和双缝衍射可以用来测量光的波长。
通过测量衍射图样的亮纹和暗纹的间距,结合已知的缝宽和缝间距,可以得到光的波长。