.
10
I= E ~ ( θ )E ~ ( θ ) *= I 0 (sα i α ) n 2 (s siN i β n β n )2
I0—一个缝在( =0)P0点产生的光强。
( sin ) 2 —单缝衍射因子。
( sin N ) 2 —多缝干涉因子。 sin
可见: 多缝衍射图样是单缝衍射和多缝干涉两因
.
24
5.缺级
缺级—干涉主极大与衍射极小位置重合时称为缺级。
dsinθ=mλ 即同时满足条件:
asinθ= nλ
.
25
由 dsinθ=mλ asinθ= nλ
(m0, 1, 2) (n1, 2)
有缺级级数:
mnd n1,2 ; a
缺级数仅与d、a有关,装置一定缺级数确定.
可见: ①缺级级数与λ、N无关; ②缺级级数m不为整数时,不为缺级
平行光垂直光栅平面入射沿n方向衍射中央主极大方向干涉0级主极大方向光栅方程干涉m级主极大方向平行光垂直单槽面入射沿n方向2dsin衍射中央主极大方向干涉0级主极大方向2dsin光栅方程干涉m级主极大方向闪耀方向
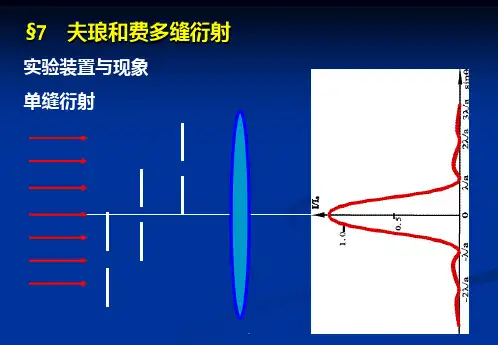
§7 夫琅和费多缝衍射
实验装置与现象 单缝衍射
.
1
多缝衍射装置
设有N条缝,每条缝宽a,不透明部分b。
.
34
由多缝衍射光强分布图可见: 决定各级光谱中光强分配的是单缝衍射因子,要改变 光谱中的能量分布,应将“能量转移”。
.
35
如何实现能量 转移呢?
.
36
1. 光线正入射时 光强分布公式
II0(sα iα n)2(ssiin N β n β)2
大部分能量集中在0级
单缝衍射主极大方向
asin, =0