第七讲 环形跑道问题

1、 掌握如下两个关系：（1）环形跑道问题同一地点出发，如果是相向而行，则每合走一圈相遇一次（2）环形跑道问题同一地点出发，如果是同向而行，则每追上一圈相遇一次2、遇见多人多次相遇、追及能够借助线段图进行分析3、用比例解、数论等知识解环形跑道问题本讲中的行程问题是特殊场地行程问题之一。

是多人（一般至少两人）多次相遇或追及的过程解决多人多次相遇与追击问题的关键是看我们是否能够准确的对题目中所描述的每一个行程状态作出正确合理的线段图进行分析。

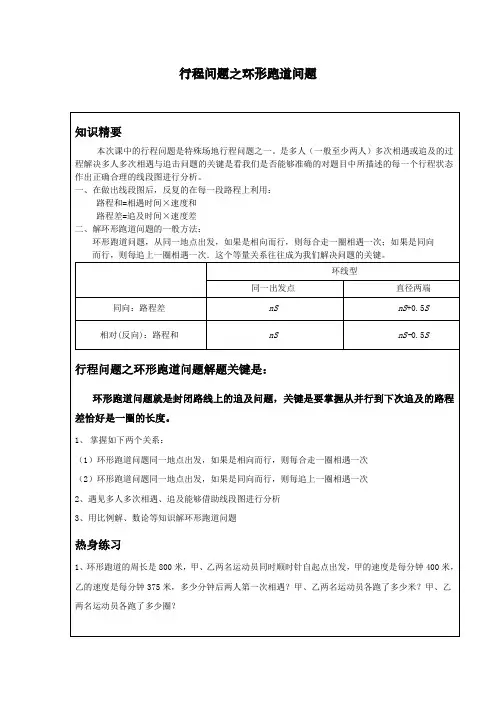
一、在做出线段图后，反复的在每一段路程上利用：路程和=相遇时间×速度和路程差=追及时间×速度差二、解环形跑道问题的一般方法：环形跑道问题，从同一地点出发，如果是相向而行，则每合走一圈相遇一次；如果是同向而行，则每追上一圈相遇一次．这个等量关系往往成为我们解决问题的关键。

环线型同一出发点直径两端 同向：路程差nS nS + 相对(反向)：路程和nS模块一、常规的环形跑道问题【例 1】 一个圆形操场跑道的周长是500米，两个学生同时同地背向而行．黄莺每分钟走66米，麻雀每分钟走59米．经过几分钟才能相遇【考点】行程问题之环形跑道 【难度】2星 【题型】解答【解析】 黄莺和麻雀每分钟共行6659125+=（千米），那么周长跑道里有几个125米，就需要几分钟，即500(6659)5001254÷+=÷=（分钟）．【答案】4分钟【巩固】 周老师和王老师沿着学校的环形林荫道散步，王老师每分钟走55米，周老师每分钟走65米。

已知林荫道周长是480米，他们从同一地点同时背向而行。

在他们第10次相遇后，王老师再走 米就回到出发点。

【考点】行程问题之环形跑道 【难度】2星 【题型】填空【关键词】希望杯,4年级,1试【解析】 几分钟相遇一次：480÷（55＋65）=4（分钟）知识精讲 教学目标环形跑道问题10次相遇共用：4×10=40（分钟）王老师40分钟行了：55×40=2200（米）2200÷480=4（圈）……280（米）所以正好走了4圈还多280米，480－280=200（米）答：再走200米回到出发点。

例1：环形跑道的周长是1000米，甲、乙两名同学同时顺时针自起点出发，甲的速度是每分钟400米，乙的速度是每分钟375米，多少分钟后两人第一次相遇？甲、乙两名同学各跑了多少米？甲、乙两同学员各跑了多少圈？
解题思路:因在环形跑道上，所以这是一道封闭路线上的追及问题，第一次相遇时，快的应比慢的多跑一圈，环形跑道的周长就是追及路程，已知了两人的速度，追及时间即是两人相遇的时间。

答案:400－375＝25（米）
1000÷25＝40（分钟）
甲：400×40＝16000(米)
乙:375×40＝15000(米)
甲:16000÷1000＝16(圈)
乙:16－1＝15(圈)
例2:：某小学有一条300米长的环形跑道，小明和小冬同时从起跑线起跑，小冬每秒钟跑6米，小明每秒钟跑4米，问小冬第一次追上小明时两人各跑了多少米，第2次追上小明时两人各跑了多少圈？
解题思路:此题第一次追上，与上一题类似，也就是快的应比慢的多跑一圈，环形跑道的周长就是追及路程，已知了两人的速度，追及时间即是两人相遇的时间。

第二次追上两人路程皆是第一次的2倍，时间也是第一次的2倍。

跑的圈数=跑的路程÷跑道长
答案：①小冬第一次追上小明所需要的时间：300÷（6－4）＝150（秒）
②小冬第一次追上小明时他所跑的路程应为：6×150＝900（米）
③小明第一次被追上时所跑的路程：4×150＝600（米）
④小冬第二次追上小明时所跑的圈数：（900×2）÷300＝6（圈）
⑤晶晶第2次被追上时所跑的圈数：（600×2）÷300＝4(圈)。

行程问题之环形跑道问题2 、幸福村小学有一条200米长的环形跑道，冬冬和晶晶同时从起跑线起跑，冬冬每秒钟跑6米，晶晶每秒钟跑4米，问冬冬第一次追上晶晶时两人各跑了多少米，第2次追上晶晶时两人各跑了多少圈？3、一条环形跑道长400米，小青每分钟跑260米，小兰每分钟跑210米，两人同时出发，经过多少分钟两人相遇4、两人在环形跑道上跑步，两人从同一地点出发，小明每秒跑3米，小雅每秒跑4米，反向而行，45秒后两人相遇。

如果同向而行，几秒后两人再次相遇5、林玲在450米长的环形跑道上跑一圈，已知他前一半时间每秒跑5米，后一半时间每秒跑4米，那么他后一半路程跑了多少秒？6、甲乙两人绕周长为1000米的环形跑道广场竞走，已知甲每分钟走125米，乙的速度是甲的2倍，现在甲在乙后面250米，乙追上甲需要多少分钟？求此圆形场地的周长？举一反三1、如图，A 、B 是圆的直径的两端，小张在A 点，小王在B 点同时出发反向行走，他们在C 点第一次相遇，C 离A 点80米；在D 点第二次相遇，D 点离B 点6O 米.求这个圆的周长.2、如图，有一个圆，两只小虫分别从直径的两端A 与C 同时出发，绕圆周相 向而行．它们第一次相遇在离A 点8厘米处的B 点，第二次相遇在离C 点处6厘米的D 点，问，这个圆周的长是多少?第一次相遇第二次相遇DC BA3、A 、B 是圆的直径的两端，甲在A 点，乙在B 点同时出发反向而行，两人在C 点第一次相遇，在D 点第二次相遇．已知C 离A 有75米，D 离B 有55米，求这个圆的周长是多少米？二、环形跑道——变道问题【例 1】如图是一个跑道的示意图，沿ACBEA 走一圈是400米，沿ACBDA 走一圈是275米，其中A 到B 的直线距离是75米．甲、乙二人同时从A 点出发练习长跑，甲沿ACBDA 的小圈跑，每100米用24秒，乙沿ACBEA 的大圈跑，每100米用21秒，问：⑴ 乙跑第几圈时第一次与甲相遇？ ⑵ 发多长时间甲、乙再次在A 相遇？三、环形跑道——变速问题【例 1】（难度等级※※）甲、乙两人沿 400 米环形跑道练习跑步，两人同时从跑道的同一地点向相反方向跑去。

环形跑道追及问题解题技巧
1. 嘿，大家知道吗，环形跑道追及问题其实没那么复杂啦！就比如说啊，甲在跑道上拼命跑，乙在后面追，这时候咋办呢？关键就是要算出速度差呀！想想看，要是你追别人，是不是得看自己比别人快多少才能知道啥时候能追上呀！所以速度差很重要哦！
2. 哇塞，遇到环形跑道追及问题不要慌呀！可以先找关键信息呀！像甲和乙的起始位置，他们的速度。

就好像你找宝藏，得先知道宝藏大概在啥地方，还有怎么去找到它的线索嘛！比如说，甲在乙前面100 米，甲每秒跑5 米，乙每秒跑 7 米，这不就可以开始算啥时候能追上了嘛！
3. 嘿呀，解决环形跑道追及问题还有一个诀窍哦，就是要算时间呀！时间就像是一把钥匙，能打开解决问题的大门呢！比如甲跑一圈要 60 秒，乙跑一
圈要 50 秒，那等乙跑完一圈的时候甲跑了多少呢？好好想想这个问题呀，
是不是很有趣呢？
4. 哦哟，环形跑道追及问题可别想得太可怕啦！要把它当成一个有趣的挑战嘛！就好像打游戏，要一关一关过呀！比如甲已经跑了半圈，乙才开始追，那这难度不就增加啦，但咱不怕呀，肯定能算出乙啥时候追到的，对不对呀！
5. 哈哈，记住啦，解决环形跑道追及问题别忘了画图呀！这就跟画地图一样，有了地图你才能知道怎么走，哪里是近路呀！比如说画出甲、乙在跑道上的位置和跑的方向，那答案是不是就清晰很多啦！
6. 哎呀呀，环形跑道追及问题其实真的不难呀！只要掌握好方法，就像掌握了一把宝剑！比如看清楚是同向追还是反向追，这很关键哟！就好像走路，知道往哪个方向走才能到目的地嘛！好啦，大家一定要记住这些技巧哦！我的观点结论就是，环形跑道追及问题并不可怕，只要学会方法就能轻松解决！。

环形跑道问题(U®1、掌握如下两个关系：（1）环形跑道问题同一地点出发，如果是相向而行，则每含走一圈相遇一次（2）环形跑道问题同一地点出发，如果是同向而行，则每追上一圈相遇一次2、遇见多人多次相遇、追及能够借助线段图进行分析3、用比例解，教论等勿识解环形跑道问题如虹本讲中的行程问题是特殊场地行程问题之一.是多人（一般至少两人）多次相遇或追及的过程解决多人多次相遇与追击问题的关键是看我们是否能够准确的对题目中所描述的每一个行程状态作出正境合理的级段图进行分析。

-、在做出线段图后，反复的在每一段路程上利用：路程和=相遇时间X速度和路程差=追及时间X速度差二、•解环形跑道问题的一般方法：环形跑道问题，从同一地点出发，如果是相向而行，则每合走一圈相遇一次：如果是同向而行,则每追上一国相遇一次.这个等量关系往往成为我们解决问题的关键。

环线型同一出发点直径两端同向：路程差nS〃S+0.5S 相对（反向）：路程和nS沾・0.55【例1]一个圆形操场跑道的周长是500米，两个学生同时同地背向而行.黄莺每分钟走66米，麻雀每分钟走59米.经过几分钟才能相遇？【解析】黄莺和麻雀每分钟共行66+59=125（千米）,那么周长跑道里有几个125米,就需要几分钟，即500+（66+59）=500-125=4（分仲）.【巩固】小张和小王各以一定速度,在周长为500米的环形跑道上跑步.小王的速度是200米/分.⑴小张和小王同时从同T&点出发，反向跑步，1分钟后两人第一次相遇，小张的速度是多少米/分？⑵小张和小王同时从同一点出发，同一方向跑步,小张跑多少圈后才能第•次追上小王？【解析】⑴两人相遇，也就是合起来跑了一个周长的行程.小张的速度是500+1-200=300（米/分）.⑵在环形的跑道上，小张要追上小王，就是小张比小王多跑一围（一个同长），因此需要的时间是：500-（300-200）=5（分）.300x5-500=3（圈）.【例2】（2008年第八届“春蕾杯”小学数学邀请赛决赛）上海小学有一长300米长的环形跑道，小亚和小胖同时从起跑线起跑，小亚每秒钟跑6米，小胖每秒钟跑4米,⑴小亚第一次追上小胖时两人各跑了多少米？（2）小亚第二次追上小胖两人各跑了多少圈？【解析】第一次追上时\小亚多跑了一国，所以需要300+（6-4）=150秒，小亚地.了6x150=900（米K 小胖跑了4x150=600（米）：第一次追上时，小胖跑了2圈，小亚跑了3圈，所以第二次追上时，小胖跑4圉.小亚跑6囹。

环形路上的行程问题1、环形运动问题：环形周长=〔大速度+小速度〕×相遇的时间环形周长=〔大速度-小速度〕×相遇的时间环形运动的追及问题和相遇问题：同时同向起点运动，第一次相遇，速度快的比速度慢的多跑一圈。

在环形跑道上同时同向，速度快的在前，慢的在后。

不是封闭的跑道追及问题，速度慢的在前，快的在后。

1.两名运发动在沿湖的环形跑道上练习长跑，甲分钟跑250米，乙每分钟跑200米，两人人同时同地同向出发，45分钟后甲追上了乙，如果两人同时同地反向而跑，经过多少钟后两人相遇？2.甲，乙两运发动在周长为400米的环形跑道上同向竞走，乙的平均速度是每分钟80米，甲的平均速度是乙的1.25倍，甲在乙前面100米处，问几分钟后，甲第1次追上乙？3.如图，A、B是圆的直径的两端，小军在A点，小勇在B点，同时出发相向而行，他俩第1次在C点相遇，C离A点50米；第2次在D点相遇，D点离B点3O米.求这个圆的周长是多少米？4.在一个长800米的环行湖边上，小明，小张两人同时从同一点出发，反向跑步，5分钟两人第一次相遇，小明每分钟跑100米，张静每分钟跑多少米？如果两人同时从同一点出发，同向跑步，多少分钟后小明能追上张静？(湘麓P29)5.有一条长400米的环形跑道，甲乙二人同时同地出发，反向而行，1分钟后第一次相遇，假设二人同时同地出发，同向而行，那么10钟后第一次相遇，假设甲比乙快，那第甲乙二人的速度分别是多少米？(湘麓P29)6.跑马场一周之长为1080。

甲乙两人骑自行车从同一地点同时出发，朝同一方向行驶，经过45分钟，甲追上乙，如果甲的速度分钟减少50米，乙的速度每分钟增加30米，从同一地点同时背向而行，那么经过3分钟两人相遇。

求原来甲，乙两人每分钟各行多少米？(湘麓P30)※7.在300米的环形跑道上，甲，乙两从同时从起跑线出发反向而跑，甲每秒跑4米，乙每秒跑6米，当他们第一次相遇在起跑点时，他们已在途中想遇多少次？(湘麓P30)8.小张和小王各以一定速度，在周长为500米的环形跑道上跑步.小王的速度是180米/分。

小学奥数：环形跑道问题环形跑道:同相向而行的等量关系:乙程-甲程=跑道长,背向而行的等量关系:乙程+甲程=跑道长。

一个周长为400米的正方形ABCD跑道,甲在B点，乙在A点，甲的速度是每秒25米，乙的速度是是每秒5米，问多长时间后甲乙第一次相遇？分析：因为是环形跑道，所以方向为逆时针，还是顺时针，不知道，所以需要分类讨论.（对于不确定的事情，又合理的问题需要分类讨论）逆时针时：可以转化为一般形成问题中的相遇问题。

把BC、CD、AD拉直，问题转化为一般的行程问题：转化为甲乙相向而行的相遇过程，其中相距的路程是300米.等量关系：甲的路程+乙的路程=相距路顺时针时：分析：因为甲的速度快，乙的速度慢，乙是追不上甲的，要想相遇，必须是甲追上乙，转化行程问题的追及问题：依上图，问题可以转化为：甲在A点，乙在B点，同时向右跑的追及问题，开始甲乙相距300米.等量关系：甲的路程-乙行的路程=相距路程转化为一般的行程问题后，问题可以迎刃而解。

这里体现了一个数学思想---转化思想，把未知的知识转化为已知的知识，把复杂的问题，转化为简单的问题，是获得新知的一个很重要的手段。

1.甲、乙两人从400米的环形跑道上一点A背向同时出发，8分钟后两人第五次相遇，已知每秒钟甲比乙多走0.1米，那么两人第五次相遇的地点与点A沿跑道上的最短路程是多少米；2.二人沿一周长400米的环形跑道均速前进，甲行一圈4分钟，乙行一圈7分钟，他们同时同地同向出发，甲走10圈，改反向出发，每次甲追上乙或迎面相遇时二人都要击掌。

问第十五次击掌时，甲走多长时间乙走多少路程？3.林玲在450米长的环形跑道上跑一圈，已知他前一半时间每秒跑5米，后一半时间每秒跑4米，那么他后一半路程跑了多少秒？4.某人在360米的环形跑道上跑了一圈，已知他前一半时间每秒跑5米，后一半时间每秒跑4米，则他后一半路程跑了多少秒？5.一条环形跑道长400米，小青每分钟跑260米，小兰每分钟跑210米，两人同时出发，经过多少分钟两人相遇（不用解方程）6.两人在环形跑道上跑步，两人从同一地点出发，小明每秒跑3米，小雅每秒跑4米，反向而行，45秒后两人相遇。

环形跑道上的追逐战：追及问题的公式与解法环形追及问题概述环形追及问题是行程问题的一种特殊类型，主要研究在环形跑道上，速度不同的两个物体，一个追赶另一个的运动规律。

这种问题在数学竞赛、智力题中经常出现，也是了解速度、时间、距离之间关系的重要课题。

公式推导基本概念：•追者：速度较快的物体。

•被追者：速度较慢的物体。

•追及时间：追者追上被追者所用的时间。

•环形跑道周长：环形跑道的长度。

公式：•追及时间= 环形跑道周长÷ (追者的速度- 被追者的速度)公式推导：假设追者和被追者同时从同一起点出发，追者速度为v1，被追者速度为v2（v1 > v2），环形跑道周长为s。

当追者追上被追者时，追者比被追者多跑了一圈，即追者比被追者多跑了s的距离。

因此，我们可以列出方程：(v1 - v2) × t = s 其中，t为追及时间。

解方程得：t = s / (v1 - v2)公式解读：这个公式告诉我们，追及时间与环形跑道周长成正比，与二者的速度差成反比。

也就是说，环形跑道越长，追及时间越长；二者的速度差越大，追及时间越短。

例题甲、乙两人在圆形跑道上跑步，甲的速度是乙的1.5倍。

如果跑道周长是400米，甲追上乙需要多少时间？解：设乙的速度为v米/秒，则甲的速度为1.5v米/秒。

根据公式：t = s / (v1 - v2) 代入数据得：t = 400 / (1.5v - v) = 800 / v (秒) 所以，甲追上乙需要800/v秒。

注意事项•单位统一：在进行计算时，一定要保证速度和距离的单位一致。

•速度差：公式中的速度差指的是追者的速度减去被追者的速度。

•特殊情况：如果追者和被追者同向而行，且速度相等，那么追者永远追不上被追者。

拓展环形追及问题还可以扩展到多个物体、不同出发点等多种情况。

对于这些复杂的问题，我们可以通过建立方程组或画图的方法来解决。

总结环形追及问题是行程问题中一个经典的模型，掌握其公式和解法对于解决相关问题具有重要意义。

本讲中的行程问题是特殊场地行程问题之一。

是多人（一般至少两人）多次相遇或追及的过程解决多人多次相遇与追击问题的关键是看我们是否能够准确的对题目中所描述的每一个行程状态作出正确合理的线段图进行分析。

一、在做出线段图后，反复的在每一段路程上利用：路程和=相遇时间×速度和路程差=追及时间×速度差二、解环形跑道问题的一般方法：环形跑道问题，从同一地点出发，如果是相向而行，则每合走一圈相遇一次；如果是同向而行，则每追上一圈相遇一次．这个等量关系往往成为我们解决问题的关键。

【例 1】上海小学有一长300米长的环形跑道，小亚和小胖同时从起跑线起跑，小亚每秒钟跑6米，小胖每秒钟跑4米，(1)小亚第一次追上小胖时两人各跑了多少米？(2)小亚第二次追上小胖两人各跑了多少圈？【考点】行程问题之环形跑道 【难度】☆☆ 【题型】解答【解析】 第一次追上时，小亚多跑了一圈，所以需要300(64)150÷-=秒，小亚跑了6150900⨯=（米）。

小胖跑了4150600⨯=（米）；第一次追上时，小胖跑了2圈，小亚跑了3圈，所以第二次追上时，例题精讲知识框架环形跑道小胖跑4圈，小亚跑6圈。

【答案】小胖跑4圈，小亚跑6圈【巩固】幸福村小学有一条200米长的环形跑道，冬冬和晶晶同时从起跑线起跑，冬冬每秒钟跑6米，晶晶每秒钟跑4米，问冬冬第一次追上晶晶时两人各跑了多少米，第2次追上晶晶时两人各跑了多少圈？【考点】行程问题之环形跑道【难度】☆☆【题型】解答【解析】这是一道封闭路线上的追及问题，冬冬与晶晶两人同时同地起跑，方向一致．因此，当冬冬第一次追上晶晶时，他比晶晶多跑的路程恰是环形跑道的一个周长(200米)，又知道了冬冬和晶晶的速度，于是，根据追及问题的基本关系就可求出追及时间以及他们各自所走的路程．①冬冬第一次追上晶晶所需要的时间：20064100（）(秒)÷-=②冬冬第一次追上晶晶时他所跑的路程应为：6100600⨯=(米)③晶晶第一次被追上时所跑的路程：4100400⨯=(米)④冬冬第二次追上晶晶时所跑的圈数：60022006（）(圈)⨯÷=⑤晶晶第2次被追上时所跑的圈数：40022004（）(圈)⨯÷=【答案】4圈【例 2】两名运动员在湖的周围环形道上练习长跑．甲每分钟跑250米，乙每分钟跑200米，两人同时同地同向出发，经过45分钟甲追上乙；如果两人同时同地反向出发，经过多少分钟两人相遇？【考点】行程问题之环形跑道【难度】☆☆【题型】解答【解析】在封闭的环形道上同向运动属追及问题，反向运动属相遇问题．同地出发，其实追及路程或相隔距离就是环形道一周的长．这道题的解题关键就是先求出环形道一周的长度．环形道一周的长度可根据两人同向出发，45分钟后甲追上乙，由追及问题，两人速度差为：25020050-=(米/分)，所以路程差为：50452250⨯=(米)，即环形道一圈的长度为2250米．所以反向出发的相遇时间为：22502502005（）(分钟)．÷+=【答案】5分钟【巩固】在400米的环形跑道上，甲、乙两人同时同地起跑，如果同向而行3分20秒相遇，如果背向而行40秒相遇，已知甲比乙快，求甲、乙的速度各是多少？【考点】行程问题之环形跑道【难度】☆☆【题型】解答【解析】甲乙的速度和为：4004010÷=(米/秒)，甲乙的速度差为：4002002÷=(米/秒)，甲的速度为：-÷=（）(米/秒)．+÷=10226（）(米/秒)，乙的速度为：10224【答案】4米/秒【例 3】周老师和王老师沿着学校的环形林荫道散步，王老师每分钟走55米，周老师每分钟走65米。

环形跑道问题1.环形跑道问题，从同一地点出发，如果是相向而行，则每相遇一次合走一圈（每隔第一次相遇时间就相遇一次）；第几次相遇就合走几圈；如果是同向而行，则每多跑一圈就追上一次（每隔第一次追及时间就追上一次）．第几次追上就多跑几圈。

2.解题方法：（1）审题：看题目有几个人或物参与；看题目时间：“再过多长时间”就是从此时开始计时，“多长时间后”就是从开始计时看地点是指是同地还是两地甚至更多。

看方向是同向、背向还是相向看事件指的是结果是相遇还是追及相遇问题中一个重要的环节是确定相遇地点，准确找到相遇地点对我们解题有很大帮助，一些是题目中直接给出在哪里相遇，有些则需要我们自己根据两人速度来判断。

追击问题中一个重要环节就是确定追上地点，从而找到路程差。

比如“用10秒钟快比慢多跑100米”我们立刻知道快慢的速度差。

这个是追击问题经常用到的，同过路程差求速度差（2）简单题利用公式（3）复杂题，尤其是多人多次相遇，一定要画路径图，即怎么走的线路画出来。

相遇问题就找路程和，追击问题就找路程差学习进阶典型例题小王、小李在某一450米环形道上(如图)散步，小王从A点，小李从B点同时出发，3分钟后小王与小李相遇，再过2分钟，小王到达B点，又再过4分钟，小王与小李再次相遇，问小王与小李每分钟各走多少米？解：根据题干分析可得：相遇后，小王与小李行驶相同的路程所用的时间之比是2：3，所以小王与小李的速度之比就是3：2，设小王的速度是3x米每分，小李的速度是2x米每分，根据题意可得方程：（3x+2x）×（4+2）=450，30x=450，x=15，小王的速度是：15×3=45（米/分），小李的速度是：15×2=30（米/分），答：小王的速度是45米/分，小李的速度是30米/分．最新试题1. 甲、乙两人同时从A点背向出发沿400米环行跑道行走，甲每分钟走80米，乙每分钟走50米，这二人最少用_____分钟再在A点相遇．2. 甲、乙两人沿400米环形跑道练习跑步，两人同时从跑道的同一地点向相反方向跑去．相遇后甲比原来速度增加2米/秒，乙比原来速度减少2米/秒，结果都用24秒同时回到原地．求甲原来的速度．(提示：环形跑道的相遇问题．)3. 一条环行跑道，每条直道长100米，两端弧道最内圈半径约32米．每条跑道宽1米．参加200米比赛时，小红在内圈第一道，小明在内圈第二道，小明在小红前面_____米处起跑．参加400米比赛时，小红在内圈第二道，小明在内圈第一道，小明在小红后面_____米处起跑．4. 一只猫追赶一只老鼠，猫和老鼠同时从平行四边形ABCD的A点出发，老鼠沿ABC方向跑，猫沿ADC方向跑，结果猫在E点将老鼠抓住了．老鼠与猫的速度比是17：20，C点与E点相距6米，猫和老鼠所跑的平行四边形的周长是多少米？5. 小明跑操场一圈要6分钟，爸爸跑一圈要3分钟，妈妈跑一圈4分钟．如果小明和妈妈同时起跑，至少多少分钟后两人在起点再次相遇？此时小明、妈妈分别跑了多少圈？6. 一个圆形跑道的周长为1200米，甲乙两人同时从同一地点沿圆周按相反方向出发，4分钟后相遇，若两人按同一方向行走，半小时后两人再次相遇，问两人速度各是多少？7. 甲、乙两人在圆形跑道上，同时从某地出发沿相反方向跑步．甲的速度是乙的3倍，他们第一次与第二次相遇地点之间的路程是100米．环形跑道有多少米？8. 爸爸妈妈在操场上跑步，妈妈每8分钟跑一圈，爸爸每6分钟跑一圈，他们同时从起点出发，至少再过几分钟又能在起点相遇？9. 甲、乙两人在400米环形跑道上练习长跑，同时从同一点出发．甲的速度是6 米/秒，乙的速度是4米/秒，乙跑几圈后，甲能超过乙一圈？10. 一只蚂蚁沿等边三角形的三条边由A点开始爬行一周．在三条边上爬行的速度分别为每分50厘米、每分20厘米、每分30厘米(如图)．它爬行一周的平均速度是_____．。

环形跑道问题，从同一地点出发，如果是相向而行，则每合走一圈相遇一次；如果是同向而行，则每追上一圈相遇一次．这个等量关系往往成为我们解决问题的关键。

环形跑道:同相向而行的等量关系:乙程-甲程=跑道长,背向而行的等量关系:乙程+甲程=跑道长。

于一个环形跑道问题的思考.一个周长为400米的正方形ABCD跑道,甲在B点，乙在A点，甲的速度是每秒25米，乙的速度是是每秒5米，问多长时间后甲乙第一次相遇？分析：因为是环形跑道，所以方向为逆时针，还是顺时针，不知道，所以需要分类讨论.（对于不确定的事情，又合理的问题需要分类讨论）逆时针时：可以转化为一般形成问题中的相遇问题。

等量关系：甲的路程+乙的路程=相距路顺时针时：分析：因为甲的速度快，乙的速度慢，乙是追不上甲的，要想相遇，必须是甲追上乙，转化行程问题的追及问题：依上图，问题可以转化为：甲在A点，乙在B点，同时向右跑的追及问题，开始甲乙相距300米.等量关系：甲的路程-乙行的路程=相距路程转化为一般的行程问题后，问题可以迎刃而解。

有一个圆形跑道周长是600米,甲在乙前面240米处, 两人同时沿顺时针方向跑.已知甲每分钟跑120米,乙每分钟跑100米,问几分钟后甲追上乙?如果追上后继续跑,问多少分钟后,甲第二次追上乙?这里体现了一个数学思想---转化思想，把未知的知识转化为已知的知识，把复杂的问题，转化为简单的问题，是获得新知的一个很重要的手段。

一个圆周长90厘米，3个点把这个圆周分成三等分，3只爬虫A，B，C分别在这3个点上.它们同时出发，按顺时针方向沿着圆周爬行.A 的速度是10厘米/秒，B的速度是5厘米/秒，C的速度是3厘米/秒，3只爬虫出发后多少时间第一次到达同一位置？解：先考虑B与C这两只爬虫，什么时候能到达同一位置.开始时，它们相差30厘米，每秒钟B能追上C（5-3）厘米0.30÷（5-3）＝15（秒）.因此15秒后B与C到达同一位置.以后再要到达同一位置，B要追上C一圈，也就是追上90厘米，需要90÷（5-3）＝45（秒）.B与C到达同一位置，出发后的秒数是15，，105，150，195，……再看看A与B什么时候到达同一位置.第一次是出发后30÷（10-5）=6（秒），以后再要到达同一位置是A追上B一圈.需要90÷（10-5）＝18（秒），A与B到达同一位置，出发后的秒数是6，24，42，，78，96，…对照两行列出的秒数，就知道出发后60秒3只爬虫到达同一位置. 答：3只爬虫出发后60秒第一次爬到同一位置.请思考， 3只爬虫第二次到达同一位置是出发后多少秒？例6绕湖一周是24千米，小张和小王从湖边某一地点同时出发反向而行.小王以4千米/小时速度每走1小时后休息5分钟；小张以6千米/小时速度每走50分钟后休息10分钟.问：两人出发多少时间第一次相遇？解：小张的速度是6千米/小时，50分钟走5千米我们可以把他们出发后时间与行程列出下表：例7甲村、乙村相距6千米，小张与小王分别从甲、乙两村同时出发，在两村之间往返行走（到达另一村后就马上返回）.在出发后40分钟两人第一次相遇.小王到达甲村后返回，在离甲村2千米的地方两人第二次相遇.问小张和小王的速度各是多少？解：画示意图如下：如图，第一次相遇两人共同走了甲、乙两村间距离，第二次相遇两人已共同走了甲、乙两村间距离的3倍，因此所需时间是例8A、B是圆的直径的两端，小张在A点，小王在B点同时出发反向行走，他们在C点第一次相遇，C离A点80米；在D点第二次相遇，D点离B点6O米.求这个圆的周长.解：第一次相遇，两人合起来走了半个周长；第二次相遇，两个人合起来又走了一圈.从出发开始算，两个人合起来走了一周半.因此，第二次相遇时两人合起来所走的行程是第一次相遇时合起来所走的行程的3倍，那么从A到D的距离，应该是从A到C距离的3倍，即A到D是例9小张和小王各以一定速度，在周长为500米的环形跑道上跑步.小王的速度是180米/分.（1）小张和小王同时从同一地点出发，反向跑步，75秒后两人第一次相遇，小张的速度是多少米/分？（2）小张和小王同时从同一点出发，同一方向跑步，小张跑多少圈后才能第一次追上小王例10.甲乙两人分别从圆形跑道直径的两端同时匀速按相反的方向绕环型跑道运动,当乙跑100米时与甲第一次相遇,甲走完一周差60米时与乙第二次相遇,求环行跑道的长度?。

一元一次方程——环形跑道问题教学目标：1.知识与技能：理解环形跑道问题就是一个封闭路线中的追击与相遇问题，掌握通向而行为追击，逆向而行为相遇。

并掌握其中的数学等量关系，列出一元一次方程解决问题。

2.过程与方法：通过动态演示，让学生理解追击中从第一次相遇到第二次相遇，运动快者的路程—运动慢者的路程=环形跑道的周长。

相遇中从第一次相遇到第二次相遇，运动快者的路程+运动慢者的路程=环形跑道的周长。

3.情感态度价值观：通过对环形跑道问题的分析，培养学生的逻辑思维能力。

教学重点：环形跑到问题中的数量关系及解题思路分析教学难点：让学生理解追击中从第一次相遇到第二次相遇运动快者比运动慢者多跑一圈。

教学过程：同学们好，在校园生活中，相信每年的春季秋季运动会一定会给同学们留下非常深刻的记忆，而最让人冲动的一定是在跑道上飞奔的长跑运动，特别是如果有人被套圈，那会把气氛推向高潮。

那么什么是套圈呢？今天我们就一起学习一下环形跑道中的追击与相遇问题。

首先环形跑道的第一类问题---追击问题。

追击问题是指甲乙两人在同一地点出发，同向而行〔甲快乙慢〕分析：那么这时两人是同一地点出发，当开始出发时，甲因为速度快，一开始就跑到了乙的前面，由以下图可知：甲追上乙时，甲肯定比乙多跑了一圈，这种情景就是赛道上的套圈。

那么甲总路程- 乙总路程= 跑道周长例1：小王、叔叔在400米长的环形跑道上练习跑步，小王每秒跑5米，叔叔每秒跑7.5米。

〔1〕假设两人同时同地反向出发，多长时间两人首次相遇？分析：由同时同地反向出发可知，这是典型的相遇问题。

即小王的路程+ 叔叔的路程= 400解：设x分钟两人首次相遇。

-x5.7=x4400解出未知数，此题可解环形跑道的第二类问题---相遇问题。

相遇问题是指甲乙两人在同一地点出发，背向〔反向〕而行〔甲快，乙慢〕分析：当甲与乙第一次相遇时，由以下图可知：甲乙共同跑了一圈。

那么甲总路程+乙总路程=跑道周长例2：小王、叔叔在400米长的环形跑道上练习跑步，小王每秒跑4米，叔叔每秒跑7.5米。

环形跑道一个周长为400米的正方形ABCD跑道,甲在B点，乙在A点，甲的速度是每秒25米，乙的速度是是每秒5米，问多长时间后甲乙第一次相遇？分析：因为是环形跑道，所以方向为逆时针，还是顺时针，不知道，所以需要分类讨论。

（对于不确定的事情，又合理的问题需要分类讨论）逆时针时：可以转化为一般形成问题中的相遇问题。

把BC、CD、AD拉直，问题转化为一般的行程问题：转化为甲乙相向而行的相遇过程，其中相距的路程是300米。

等量关系：甲的路程+乙的路程=相距路顺时针时：分析：因为甲的速度快，乙的速度慢，乙是追不上甲的，要想相遇，必须是甲追上乙，转化行程问题的追及问题：依上图，问题可以转化为：甲在A点，乙在B点，同时向右跑的追及问题，开始甲乙相距300米。

等量关系：甲的路程-乙行的路程=相距路程转化为一般的行程问题后，问题可以迎刃而解。

这里体现了一个数学思想-转化思想，把未知的知识转化为已知的知识，把复杂的问题，转化为简单的问题，是获得新知的一个很重要的手段。

环形跑道问题，从同一地点出发，如果是相向而行，则每合走一圈相遇一次；如果是同向而行，则每追上一圈相遇一次．这个等量关系往往成为我们解决问题的关键。

封闭环形上的相遇问题：环形周长÷速度和=相遇时间封闭环形上的追及问题：环形周长÷速度差=追及时间例1：如图，A、B是圆的直径的两端，小张在A点，小王在B点同时出发反向行走，他们在C点第一次相遇，C离A点80米；在D点第二次相遇，D点离B点60米。

求这个圆的周长。

解：第一次相遇，两人合起来走了半个周长；第二次相遇，两个人合起来又走了一圈。

从出发开始算，两个人合起来走了一周半。

因此，第二次相遇时两人合起来所走的行程是第一次相遇时合起来所走的行程的3倍，那么从A到D的距离，应该是从A到C距离的3倍，即A到D是803＝240（米）。

240-60=180（米）。

1802＝360（米）。

答：这个圆的周长是360米。

环形跑道知识框架本讲中的行程问题是特殊场地行程问题之一。

是多人（一般至少两人）多次相遇或追及的过程解决多人多次相遇与追击问题的关键是看我们是否能够准确的对题目中所描述的每一个行程状态作出正确合理的线段图进行分析。

一、在做出线段图后，反复的在每一段路程上利用：路程和=相遇时间×速度和路程差=追及时间×速度差二、解环形跑道问题的一般方法：环形跑道问题，从同一地点出发，如果是相向而行，则每合走一圈相遇一次；如果是同向而行，则每追上一圈相遇一次．这个等量关系往往成为我们解决问题的关键。

例题精讲【例 1】上海小学有一长300米长的环形跑道，小亚和小胖同时从起跑线起跑，小亚每秒钟跑6米，小胖每秒钟跑4米，(1)小亚第一次追上小胖时两人各跑了多少米？(2)小亚第二次追上小胖两人各跑了多少圈？【考点】行程问题之环形跑道【难度】☆☆【题型】解答【解析】第一次追上时，小亚多跑了一圈，所以需要300(64)150⨯=（米）。

÷-=秒，小亚跑了6150900小胖跑了4150600⨯=（米）；第一次追上时，小胖跑了2圈，小亚跑了3圈，所以第二次追上时，小胖跑4圈，小亚跑6圈。

【答案】小胖跑4圈，小亚跑6圈【巩固】幸福村小学有一条200米长的环形跑道，冬冬和晶晶同时从起跑线起跑，冬冬每秒钟跑6米，晶晶每秒钟跑4米，问冬冬第一次追上晶晶时两人各跑了多少米，第2次追上晶晶时两人各跑了多少圈？【考点】行程问题之环形跑道【难度】☆☆【题型】解答【解析】这是一道封闭路线上的追及问题，冬冬与晶晶两人同时同地起跑，方向一致．因此，当冬冬第一次追上晶晶时，他比晶晶多跑的路程恰是环形跑道的一个周长(200米)，又知道了冬冬和晶晶的速度，于是，根据追及问题的基本关系就可求出追及时间以及他们各自所走的路程．①冬冬第一次追上晶晶所需要的时间：20064100（）(秒)÷-=②冬冬第一次追上晶晶时他所跑的路程应为：6100600⨯=(米)③晶晶第一次被追上时所跑的路程：4100400⨯=(米)④冬冬第二次追上晶晶时所跑的圈数：60022006（）(圈)⨯÷=⑤晶晶第2次被追上时所跑的圈数：40022004（）(圈)⨯÷=【答案】4圈【例 2】两名运动员在湖的周围环形道上练习长跑．甲每分钟跑250米，乙每分钟跑200米，两人同时同地同向出发，经过45分钟甲追上乙；如果两人同时同地反向出发，经过多少分钟两人相遇？【考点】行程问题之环形跑道【难度】☆☆【题型】解答【解析】在封闭的环形道上同向运动属追及问题，反向运动属相遇问题．同地出发，其实追及路程或相隔距离就是环形道一周的长．这道题的解题关键就是先求出环形道一周的长度．环形道一周的长度可根据两人同向出发，45分钟后甲追上乙，由追及问题，两人速度差为：25020050-=(米/分)，所以路程差为：50452250⨯=(米)，即环形道一圈的长度为2250米．所以反向出发的相遇时间为：22502502005（）(分钟)．÷+=【答案】5分钟【巩固】在400米的环形跑道上，甲、乙两人同时同地起跑，如果同向而行3分20秒相遇，如果背向而行40秒相遇，已知甲比乙快，求甲、乙的速度各是多少？【考点】行程问题之环形跑道【难度】☆☆【题型】解答【解析】甲乙的速度和为：4004010÷=(米/秒)，甲的速度为：÷=(米/秒)，甲乙的速度差为：4002002（）(米/秒)．-÷=10226（）(米/秒)，乙的速度为：10224+÷=【答案】4米/秒【例 3】周老师和王老师沿着学校的环形林荫道散步，王老师每分钟走55米，周老师每分钟走65米。

奥数行程问题——环形跑道行程问题——环形跑道环形跑道问题就是封闭路线上的追及问题，关键是要掌握从并行到下次追及的路程差恰好是一圈的长度。

1、相遇问题：题型特点：甲、乙两人同时从同地反向出发。

解题规律：两人相遇时一起走一圈（跑道周长）。

之后每见面一次，就一起走1圈；见面n次，两人一起走n个周长。

2、追及问题：题型特点：甲、乙两人同时从同地同向出发。

解题规律：开始出发时由于速度不同两人之间的距离会越来越远，之后快的会追上慢的，此时快的人比慢的人多走1圈（路程差为跑道周长）。

之后每追上一次，就多走1圈；追上n次，快的就比慢的多走n个周长。

3、需要处理的问题：a、环形跑道中速度、时间、路程之间的关系处理。

b、多次追及问题的处理。

c、不同地点出发的追及问题。

1、一个圆形荷花池的周长为400米，甲、乙两人绕荷花池顺时针跑步。

甲每分钟跑250米，乙每分钟跑200米，现在甲在乙后面50米，甲第二次追上乙需要多少分钟？2、一条环形跑道长400米，小青每分钟跑260米，小兰每分钟跑140米，两人同时反向出发，经过几分钟两人相遇？3、上海小学有一长300米长的环形跑道，小亚和小胖同时从起跑线起跑，小亚每秒钟跑6米，小胖每秒钟跑4米，小亚第一次追上小胖时，小胖跑了多少米？4、幸福村小学有一条200米长的环形跑道，冬冬和晶晶同时从起跑线起跑，冬冬每秒钟跑6米，晶晶每秒钟跑4米，问冬冬第2次追上晶晶时，冬冬跑了多少圈？5、甲、乙二人骑自行车从环形公路上的同一地点出发，背向而行。

现在已知甲走一圈的时间为75分钟，如果在出发后第50分钟甲、乙两人相遇，那么乙走一圈的时间是多少分钟？6、甲、乙二人骑自行车从环形公路上同一地点同时出发，背向而行.现在已知甲走一圈的时间是70 分钟，如果在出发后45分钟甲、乙二人相遇，那么乙走一圈的时间是多少分钟?7、两名运动员在湖的周围环形道上练习长跑．甲每分钟跑250米，乙每分钟跑200米，两人同时同地同向出发，经过45分钟甲追上乙；如果两人同时同地反向出发，经过几分钟两人相遇？8、在400米的环形跑道上，甲、乙两人同时同地起跑，如果同向而行3分20秒相遇，如果背向而行40秒相遇，已知甲比乙快，求甲的速度是多少米/秒？9、环形跑道的周长是800米，甲乙两名运动员同时顺时针自起点出发，甲的速度是每分钟400米，乙的速度是每分钟375米。