三角形稳定性和四边形不稳定

《三角形的稳定性》教材分析本节是人民教育出版社义务教育教科书《数学》八年级上册第十一章《三角形》的第3节《三角形的稳定性》的教学内容，本节课是理解掌握三角形的有关概念的基础上，通过观察和实地操作得到三角形具有稳定性，四边形没有稳定性，稳定性与没有稳定性在生产、生活中广泛应用。

教学目标通过观察和实地操作得到三角形具有稳定性，四边形没有稳定性，稳定性与没有稳定性在生产、生活中广泛应用.教学重难点【教学重点】了解三角形稳定性在生产、生活是实际应用【教学难点】准确使用三角形稳定性与生产生活之中课前准备多媒体课件、教具等．教学过程（一）导入新课如图，盖房子时，在窗框未安装好之前，木工师傅常常先在窗框上斜钉一根木条，为什么要这样做呢？【设计意图】：学生联系生活，激发学生的学习兴趣。

（二）讲授新课观察上面这些图片，你发现了什么？发现这些物体都用到了三角形，为什么呢？这说明三角形有它所独有的性质，是什么呢？我们通过实验来探讨三角形的特性。

探究：1. 用三根木条用钉子钉成一个三角形木架，然后扭动它，它的形状会改变吗？2. 用四根木条用钉子钉成一个四边形木架，然后扭动它，它的形状会改变吗？3. 在四边形的木架上再钉一根木条，将它的一对顶点连接起来，然后扭动它，它的形状会改变吗？归纳总结：从上面实验过程你能得出什么结论？与同伴交流．三角形木架形状不会改变，四边形木架形状会改变，这就是说，三角形具有稳定性，四边形没有稳定性．还可以发现，斜钉一根木条的四边形木架的形状不会改变。

这是为什么呢？答：斜钉一根木条后，四边形变成两个三角形，由于三角形有稳定性，所以斜钉一根木条的四边形木架的形状不会改变。

四边形的不稳定性是我们常常需要克服的，那么四边形的不稳定性在生活中有没有应用价值呢？如果有，你能举出实例吗？【设计意图】：学生根据问题自主探究，解决问题学生活动：独立探究学习、思考，合作交流后回答。

培养学生合作交流的能力.（三）重难点精讲理解“稳定性”“只要三角形三条边的长度固定，这个三角形的形状和大小也就完全确定，三角形的这种性质叫做三角形的稳定性。

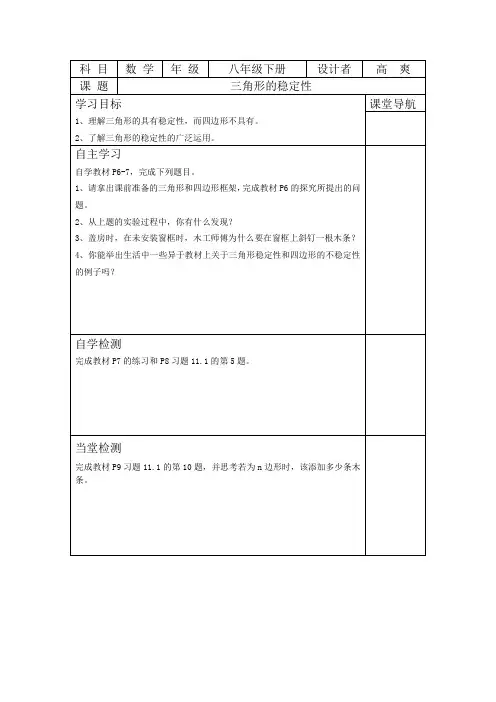
科目数学年级八年级下册设计者高爽课题三角形的稳定性
学习目标
课堂导航
1、理解三角形的具有稳定性，而四边形不具有。

2、了解三角形的稳定性的广泛运用。

自主学习
自学教材P6-7，完成下列题目。

1、请拿出课前准备的三角形和四边形框架，完成教材P6的探究所提出的问
题。

2、从上题的实验过程中，你有什么发现？
3、盖房时，在未安装窗框时，木工师傅为什么要在窗框上斜钉一根木条？
4、你能举出生活中一些异于教材上关于三角形稳定性和四边形的不稳定性
的例子吗？
自学检测
完成教材P7的练习和P8习题11.1的第5题。

当堂检测
完成教材P9习题11.1的第10题，并思考若为n边形时，该添加多少条木
条。

《三角形的稳定性》教学设计《三角形的稳定性》教学设计范文（精选3篇）《三角形的稳定性》教学设计1教学目标：通过观察和实地操作得到三角形具有稳定性，四边形没有稳定性，稳定性与没有稳定性在生产、生活中广泛应用重点：了解三角形稳定性在生产、生活是实际应用难点：准确使用三角形稳定性与生产生活之中课前准备：小木条8个，小钉若干教学过程：一、看一看，想一想课本P73投影出来二、做一做1、用三根木条用钉子钉成一个三角形木架，然后扭动它，它的形状会改变吗？2、用四根木条用钉子钉成一个四边形木架，然后扭动它，它的形状会改变吗？3、在四边形的木架上再钉一根木条，将它的一对顶点连接起来，然后扭动它，它的`形状会改变吗？三、议一议从上面实验过程你能得出什么结论？与同伴交流。

三角形木架形状不会改变，四边形木架形状会改变，这就是说，三角形具有稳定性，四边形没有稳定性。

四、三角形稳定性应用举例、四边形没有稳定性的应用举例五、练一练课本P74练习作业：课本P75――5,9《三角形的稳定性》教学设计2教学目标：知识与能力：了解三角形的稳定性过程与方法：知道三角形的稳定性在实际生活中的应用情感态度与价值观：通过对问题的解决，使学生有成就感，培养学生的合作精神教学重点：三角形的稳定性教学难点：三角形的稳定性在实际生活中的应用教学过程：一、情景诱导盖房子时，在窗框未安装好之前，木工师傅常常先在窗框上斜定一根木条，如图，为什么要这样做呢？（三角形的稳定性）这节课我们就来学习三角形的稳定性。

二、探究指导（学生按照探究提纲学习；教师做板书准备后，到学生中巡回指导，掌握学生的情况，为展示归纳做准备）（一）探究提纲：1、将三根木条用钉子定成一个三角形木架，然后扭动它，它的形状会变吗？（不会）2、将四根木条定成一个四边形木架，然后扭动它，它的形状会变吗？（会）3、如果在四边形木架上再定一根木条，将它的一对顶点连接起来，再扭动它，这时木架的形状还会改变吗？（不会）4、你发现什么规律？你能用一句话把这个规律叙述出来吗？三、展示归纳1、教师准备教具，学生逐题上前操作汇报2、发动学生评价、完善四、变式练习（一二口答，其它逐题出示，让学生练习，教师做必要的板书准备，然后巡回指导，了解情况；抽有一定问题的同学汇报，生说师写；发动其他同学评价、补充和完善；老师给予必要的强调，画龙点睛。

人教版_部编版八年级数学上册第十一章第一节三角形的稳定性试题（含答案)一、单选题1．下列图形具有稳定性的是（）A．菱形B．矩形C．三角形D．正方形【答案】C【解析】【分析】根据三角形具有稳定性，四边形具有不稳定性进行判断．【详解】解：三角形具有稳定性，而四边形具有不稳定性．故选：C．【点睛】本题考查了三角形的稳定性，难度不大，属于基础题型.2．如图，在生活中，我们经常会看见如图所示的情况，在电线杆上拉两条钢筋，来加固电线杆，这是利用了三角形的（）A．稳定性B．灵活性C．对称性D．全等性【答案】A【解析】【分析】三角形的特性之一就是具有稳定性．【详解】解：这是利用了三角形的稳定性．故选A．【点睛】此题考查三角形的稳定性，解题关键在于掌握其性质定义.3．将五根木棒按如下四种情形钉在一起，其整体结构不会发生变形，最稳定的是( )\A．B．C．D．【答案】A【解析】【分析】根据三角形具有稳定性，而四边形不具有进行判断.【详解】A选项：有两个三角形组成，故具有稳定性；B选项：有一个四边形，四边形不具有稳定性，故四边形部分不具有稳定性；C选项：有一个四边形，四边形不具有稳定性，故四边形部分不具有稳定性；D选项：有一个四边形，四边形不具有稳定性，故四边形部分不具有稳定性；故选：A.【点睛】考查了三角形的稳定性，解题关键是抓住图形中有没有四边形，因为四边形不具有稳定性.4．下列图形中具有稳定性的是（）A．长方形B．锐角三角形C．正六边形D．平行四边形【答案】B【解析】【分析】根据几何图形中三角形具有稳定性可知B答案正确．【详解】根据三角形具有稳定性，四边形、六边形都不具有稳定性，可知B答案符合题意要求．故选：B．【点睛】本题主要考查了三角形的稳定性，在几何图形中只有三角形具有稳定性，而四边形以及四边以上的多边形都不具有稳定性．5．不是利用三角形稳定性的是：（）A．自行车的三角形车架B．三角形房架C．大桥斜拉铁索D．伸缩门【答案】D【解析】利用三角形的稳定性进行解答．【详解】解：由四边形组成的伸缩门是利用了四边形的不稳定性，而A、B、C选项都是利用了三角形的稳定性，故选：D．【点睛】本题考查了三角形的稳定性，当三角形三边的长度确定后，三角形的形状和大小就能唯一确定下来，故三角形具有稳定性．6．下列图形具有稳定性的是( )A．锐角三角形B．正方形C．五边形D．六边形【答案】A【解析】【分析】根据三角形具有稳定性，可得答案．【详解】解：A、锐角三角形具有稳定性，故此选项正确；B、正方形不具有稳定性，故此选项错误；C、五边形不具有稳定性，故此选项错误；D、六边形不具有稳定性，故此选项错误；故选：A．本题主要考查三角形的性质，关键是掌握三角形具有稳定性．7．下列图形不具有稳定性的是（）A．正方形B．等腰三角形C．直角三角形D．钝角三角形【答案】A【解析】【分析】三角形具有稳定性，其它多边形不具有稳定性．【详解】解：根据三角形的稳定性可得，B、C、D都具有稳定性，不具有稳定性的是A选项，故选A．【点睛】本题主要考查三角形稳定性，解决本题的关键是要熟练掌握三角具有稳定性，四边形不具有稳定性.8．下列图形中不具有稳定性的是（）A．锐角三角形B．长方形C．直角三角形D．等腰三角形【答案】B【解析】【分析】三角形具有稳定性，根据三角形的性质，四边形的性质可得答案．【详解】长方形属于四边形，不具有稳定性，而三角形具有稳定性，故B符合题意；【点睛】本题考查了多边形和三角形的稳定性，解决问题的关键是利用了四边形的不稳定性．9．下列图形具有稳定性的是（）A．正五边形B．正方形C．梯形D．等腰三角形【答案】D【解析】【分析】根据三角形具有稳定性即可解答.【详解】解:因为三角形具有稳定性,所以正五边形,正方形,梯形,等腰三角形中具有稳定性的是等腰三角形.所以D选项是正确的.【点睛】本题考查了三角形的稳定性,三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等.10．下列图形中，不具有稳定性的是（）A．B．C．D．【答案】D【分析】根据三角形具有稳定性，四边形不具有稳定性即可判断．【详解】因为三角形具有稳定性，四边形不具有稳定性，故选D．【点睛】本题考查三角形的稳定性，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．。

四边形章节涉及的15个易错点精编精讲【知识点1】一、多边形与正多边形的概念1.在平面内，由一些线段首尾顺次相接组成的封闭图形叫作多边形2.在平面内，边相等，角也相等的多边形叫作正多边形二、多边形的内角和1.n边形的内角和等于（n-2）·180o2.任意多边形的外角和等于360o三、四边形的不稳定性三角形具有稳定性，四边形具有不稳定性易错点1 对多边形的截线问题考虑不全面，从而漏解例题1一个多边形截去一个角后，形成另一个多边形的内角和为720°，那么原多边形的边数为（）A.5B.5或6C.5或7D.5或6或7【错解】A【错因】首先求得内角和为720°的多边形的边数，即可确定原多边形的边数，设内角和为720°的多边形的边数是n，则（n-2）·180°=720°，解得n=6.错解是错误地认为截去一个角，多边形的内角就少了一个，从而得出原多边形的变数为5.由图2-1可知，五边形、六边形、七边形截去一个角后都可以得到六边形，故原边形的边数为5或6或7.【正解】由图2-1可知，五边形、六边形、七边形截去一个角后都可以得到六边形，故原边形的边数为5或6或7，故选D巩固1 内角和为540°的多边形截去一个角后，形成的新多边形的边数为（）A.4B.5C.6D.4或5或6【错解】A【正解】D【小结】结合图形很容易得出，一个多边形截去一个内角后，边数可能减l，可能不变，可能加1，反之，截去一个内角所得的多边形的边数比原多边形的边数可能少1，可能多1，也有可能相等。

易错点2 对多边形内角及内角和的取值(范围)认识不够全面，解题陷入误区例题2小华在进行多边形内角和计算时，求得的内角和为1680°，当发现错了之后，重新检查，发现少加了一个内角，则这个内角是多少度？他求的是几边形的内角和?【错解】设这个多边形的边数为n.由题意，得(n-2)×180°=1680°1680°不是180°的整数倍此题无解。