如何判别反褶积的效果
- 格式:docx
- 大小:43.46 KB
- 文档页数:4

反褶积及其应用刘能强(中油测井技术服务有限责任公司 北京100043) 摘要 Schroeter、H ollaender和G ringarten等人解决了反褶积计算方法上稳定性问题,使反褶积方法应用于试井解释。
从反褶积的意义入手,论述了反褶积方法和Schroeter方法及其在试井解释中的应用。
反褶积方法存在一定局限性,但实例说明,它能综合测试全过程所探测的信息,帮助正确确定模型,得出比常规解释更多、更可靠的解释结果,是一个很有用的新方法、新工具。
关键词 褶积 反褶积 试井解释 应用 非线性回归引 言褶积(又名卷积)和反褶积(又名去卷积)是一种积分变换的数学方法,在许多方面得到了广泛应用。
用褶积解决试井解释中的问题,早就取得了很好成果;而反褶积,直到最近,Schroeter、H ollaender和G ringarten等人解决了其计算方法上的稳定性问题,使反褶积方法很快引起了试井界的广泛注意。
有专家认为,反褶积的应用是试井解释方法发展史上的又一次重大飞跃。
他们预言,随着测试新工具和新技术的增加和应用,以及与其它专业研究成果的更紧密结合,试井在油气藏描述中的作用和重要性必将不断增大。
反褶积方法由实测资料构造出理想的、等效的、对应于相同时间段内以恒定产量生产条件下的压力变化,由此得到测试全部历程的压力响应,其探测范围要大得多,而且不存在叠加计算所带来的影响,也不存在产量史的不完整而造成的误差。
寻找到这些信息,便可获得比常规试井解释更多、更可靠的测试解释结果———这就是反褶积的大意和意义。
1.反褶积从测试录取得到的资料是产量变化史q(t)和压力变化史Δp(t),这就是试井解释的对象,而试井解释的任务就是从这些资料识别测试层和测试井的类型并算出它们的各种参数。
实际上,由实测的压力变化和产量资料计算dΔp udln t=t・Δp u′,是解释过程中至关要紧的一个步骤。
根据杜哈美(Duhamel)原理,得到研究压力降落和压力恢复的褶积方程为p(t)=p i-∫t0q(τ)9Δp u(t-τ)9(t-τ)dτ=p i-∫t0q(τ)Δp′u(t-τ)dτ(1)Δp(t)=pi-p(t)=∫t0q(τ)9Δp u(t-τ)9(t-τ)dτ=∫t0q(τ)Δp′u(t-τ)dτ(2)其中 Δpu=Kh0.9210qμBΔpΔp=pi-p wf(t)式中:pwf(t)———开井生产t时刻井底压力,MPa;t———测试井开井生产时间,h;q———测试井产量,m3Πd;p i———原始地层压力,MPa;Δpu———重整压力或单位产量下重整压力响应(以恒定1单位产量生产所造成压力变化)。

系统熵反褶积概述系统熵反褶积是一种用于图像处理和信号处理的数学运算方法,可以有效地去除图像或信号中的噪声,并提高其清晰度和可视化效果。
本文将详细介绍系统熵反褶积的原理、应用以及未来的发展方向。
一、系统熵反褶积的原理系统熵反褶积的原理基于信息熵的概念。
信息熵是信息论中的一个重要概念,用于衡量信号或数据中的不确定性程度。
在图像处理中,系统熵反褶积通过最小化图像的信息熵来实现去噪和增强的效果。
系统熵反褶积的过程可以分为以下几个步骤:1. 首先,将原始图像进行离散傅里叶变换(DFT),得到图像的频域表示。
2. 然后,计算图像频域的功率谱密度,并取对数得到系统熵。
3. 接下来,对系统熵进行反褶积处理,即将系统熵的对数值取反。
4. 最后,将反褶积后的系统熵进行逆变换,得到增强后的图像。
二、系统熵反褶积的应用系统熵反褶积在图像处理和信号处理中有广泛的应用。
以下是几个重要的应用领域:1. 医学图像处理:系统熵反褶积可以用于去除医学图像中的噪声,并提高图像的清晰度,从而帮助医生更准确地诊断疾病。
2. 遥感图像处理:系统熵反褶积可以用于去除遥感图像中的噪声,并增强图像的细节,从而提高图像的识别和分析能力。
3. 视频增强:系统熵反褶积可以用于对视频进行去噪和增强处理,提高视频的清晰度和可视化效果。
4. 语音信号处理:系统熵反褶积可以用于去除语音信号中的噪声,并提高语音信号的质量和可懂度。
三、系统熵反褶积的发展方向随着科学技术的不断进步,系统熵反褶积在未来还有很大的发展空间。
以下是一些可能的发展方向:1. 算法优化:目前的系统熵反褶积算法还存在一些问题,如计算复杂度较高、对噪声类型的适应性较差等。
未来的研究可以致力于优化算法,提高计算效率和噪声抑制效果。
2. 多模态融合:系统熵反褶积可以与其他图像处理算法结合,如深度学习、卷积神经网络等,进行多模态融合,提高图像处理的效果和性能。
3. 实时处理:目前的系统熵反褶积算法主要适用于离线处理,未来的研究可以将其应用于实时处理,满足实时图像处理的需求。

如何判断一幅图像是否已经应用了”反锯齿”效果?一、什么是反锯齿效果?反锯齿是一种图像处理技术,旨在消除锯齿状边缘,使图像边缘变得更平滑,更自然。
当图像边缘有锯齿状呈现时,我们常常会说这幅图像没有应用反锯齿效果。
那么,我们如何判断一幅图像是否已经应用了反锯齿效果呢?下面将详细介绍几种判断方法。
二、判断方法一:观察图像边缘是否平滑通过观察图像边缘的锯齿状情况,可以初步判断图像是否应用了反锯齿效果。
一幅经过反锯齿处理的图像,其边缘会呈现出相对平滑的状态,而没有明显的锯齿状。
在放大图像时,可以更加清晰地观察到边缘的变化情况。
如果观察到图像边缘有明显的锯齿状,那么这幅图像很可能没有应用反锯齿效果。
三、判断方法二:检测图像的分辨率图像的分辨率也是判断图像是否应用了反锯齿效果的一个重要指标。
一幅经过反锯齿处理的图像,其分辨率通常较高,可以保证图像边缘的细节更加清晰。
相反,如果图像的分辨率较低,边缘细节模糊不清,那么这幅图像很可能没有应用反锯齿效果。
可以通过查看图像属性或使用图像处理软件来获取图像的分辨率信息。
四、判断方法三:使用专业图像处理软件为了更准确地判断一幅图像是否应用了反锯齿效果,可以使用专业的图像处理软件进行分析。
这些软件通常提供了丰富的图像处理功能,可以直观地查看图像的反锯齿处理情况。
通过选择适当的工具和参数,可以对图像进行放大、检测锯齿状等操作,从而判断图像是否经过反锯齿处理。
五、判断方法四:了解图像源文件的处理过程有时候,我们无法直接判断一个图像是否应用了反锯齿效果。
这时,我们可以尝试了解图像源文件的处理过程。
如果图像的出处是经过专业处理的,如摄影作品、设计图等,那么很可能已经应用了反锯齿效果。
而一些抓取自互联网或其他渠道的图像,由于处理过程不可控,可能没有应用反锯齿效果。
综上所述,判断一幅图像是否已经应用了反锯齿效果可以通过观察图像边缘是否平滑、检测图像的分辨率、使用专业图像处理软件以及了解图像源文件的处理过程来进行。

维纳滤波反褶积维纳滤波反褶积是数字信号处理中一种重要的滤波技术,它可以帮助我们恢复由于褶积模糊造成的图像模糊。
在本文中,我将详细介绍维纳滤波反褶积的原理和应用。
一、维纳滤波反褶积的原理维纳滤波反褶积是一种通过对图像进行反褶积和滤波来恢复原始图像的方法。
根据维纳滤波反褶积的定义,它可以被定义为一种优化滤波方法,旨在通过最小化重建图像与理论模型之间的误差来恢复模糊图像的清晰度。
具体来说,维纳滤波反褶积利用噪声模型、图像抖动以及空间频率响应函数等信息来计算一个最佳的滤波器,该滤波器可以最小化图像退化过程所引起的噪声和失真。
通过使用正则化技术,维纳滤波反褶积可以对噪声和信号之间的平衡进行调整,并以最小化总方差为目标来选择最佳的滤波器。
二、维纳滤波反褶积的应用维纳滤波反褶积广泛应用于遥感图像处理、医学成像、地震学、天文学等领域,在这些领域中需要准确的图像重建和图像去噪。
例如,在医学成像中,由于诸如运动伪影、伽马射线散射等因素而导致的图像模糊,会严重影响诊断的准确性。
因此,维纳滤波反褶积可以帮助医生恢复丢失的细节并提高图像质量。
此外,维纳滤波反褶积还在工业品质检测、机器视觉等领域中得到了广泛应用。
例如,在制造业中,图像模糊可能会导致产品质量问题,而维纳滤波反褶积可以找到并消除这些模糊。
三、维纳滤波反褶积的优缺点维纳滤波反褶积作为一种优化方法,在实践中仍然具有一些优缺点。
优点:维纳滤波反褶积可以通过最小化重建图像与理论模型之间的误差来恢复图像,因此它可以有效减少噪声和提高图像质量。
此外,该方法还具有灵活性,可以根据具体情况进行优化,例如可以通过修改正则化参数来调整噪声和信号之间的平衡。
缺点:像维纳滤波反褶积这样的优化问题通常需要进行计算,因此需要一些计算资源和时间。
此外,在图像中存在大量噪声时,维纳滤波反褶积可能会变得复杂和不稳定。
四、总结总体而言,维纳滤波反褶积是一种强大的数字信号处理技术,能够在图像模糊处理、去噪等方面发挥重要作用。
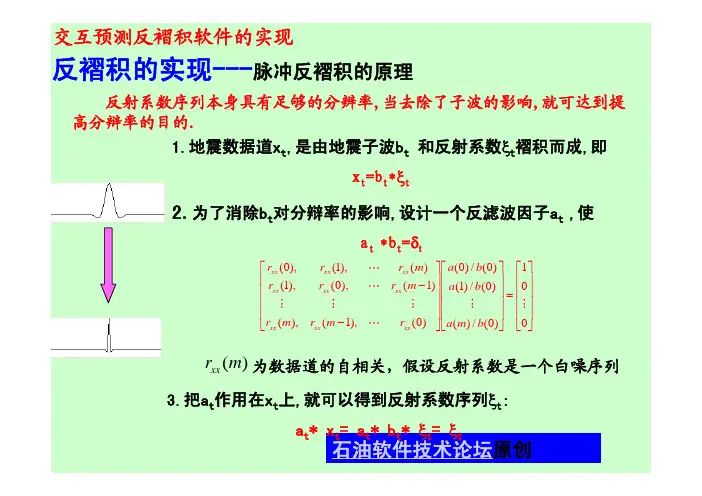


地表一致性反褶积方法浅析及应用佚名【摘要】提高地震资料分辨率的重要手段是采用反褶积技术。
反褶积方法很多,如子波反褶积、脉冲反褶积和预测反褶积等。
这些方法各有优缺点,在高分辨率资料处理中应用受到许多条件制约,不能有效地提高资料的分辨率,其效果不能满足解释人员的要求。
作地表一致性反褶积需要对记录进行频谱分析和频谱分解,同时要设计反褶积算子,然后在共炮点域和共接收点域分两步对资料进行褶积。
这种方法能够展宽频谱,压缩地震子波,并能校正地震信号的相位谱,输出零相位子波,较大程度地提高地震资料的分辨率。
该方法在高邮西部地区地震资料处理中取得较好效果。
【期刊名称】《内蒙古石油化工》【年(卷),期】2012(000)010【总页数】4页(P126-129)【关键词】地表一致性反褶积;提高信躁比;设计反褶积算子【正文语种】中文【中图分类】P631.4高分辨率地震勘探技术是一个系统工程。
在高分辨率地震资料处理的系统工程中,关键问题是新的噪音衰减技术、反褶积方法、动静校正方法和叠加成像方法四大环节和贯穿各种新技术于一体的处理流程。
反褶积方法是地震资料处理过程中的重要手段。
资料分辨率主要取决于地震波的频谱,它包括两方面的含义,即频带宽度和相位一致性。
高分辨率的地震资料应当有宽频带和零相位的频谱,改善地震波频谱的有效手段之一是反褶积技术[1]。
资料处理中应用的反褶积方法很多,每一种反褶积方法都是建立在一定假设条件下的地震褶积模型之上。
所以,反褶积的效果大都取决于所采用的褶积模型与实际地震记录的符合程度。
地表一致性反褶积是基于经过噪音衰减、速度滤波和真振幅恢复后的地震记录,对记录进行反褶积的频谱分析、反褶积频谱分解、反褶积算子设计以及对记录进行反褶积算子的应用来完成。
处理过程中在共炮点域和共接收点域进行两次反褶积,能展宽频谱,压缩地震子波,校正地震信号的相位谱,输出零相位子波,较大程度地提高地震资料分辨率[2]。
1.1 反褶积应用公式经过噪音衰减、速度滤波和真振幅恢复后的地震记录可以表示为[3]:式中,S(t,x)为偏移距为X的地震道,r(t)为反射系数序列,T 1(t,τ)为时变传输和多次波效应,M (t,x)为与偏移距有关的时差效应,SL(t)为排列损失和球面发散损失,T2(t,τ)为时变吸收或非弹性衰减效应,R 1(t,x)为与偏移距有关的浅层混响记录系统响应,W(t)为震源子波,N(t)为噪音。


位场欧拉反褶积方法适用性分析及其应用罗潇;王彦国;张瑾;邓居智;吴姿颖;陈姝霓【摘要】欧拉反褶积是重磁勘探常用的反演方法和资料解释工具.从单一场源出发,推导了叠加场源下的常规欧拉反褶积公式,理论分析出了异常叠加是影响常规欧拉反褶积应用效果的主要因素.为解决这一问题,可采用高阶导数来提高异常分辨率,削弱叠加影响,但高阶导数却易受高频干扰影响.为了深入研究欧拉反褶积方法的应用效果及其适用性,利用垂向导数形式的欧拉反褶积与常规欧拉反褶积进行对比分析.模型试验表明:在无噪声情况,基于垂向一阶导数的欧拉反褶积反演结果具有更高的聚合度和计算精度,可有效压制异常叠加影响;但当原异常含有噪声时,基于垂向导数的欧拉反褶积受噪声影响严重,反演效果不如常规方法,可以采用向上延拓方法来压制噪声干扰以提高高阶导数欧拉反褶积的反演精度.在江西相山实际重力资料处理中,垂向一阶导数的欧拉反褶积比常规欧拉反褶积反演出了更多的地质边界信息,而常规欧拉反褶积在主构造上反演点的连续性更强.因此,在实际资料处理中,建议常规欧拉反褶积和导数形式下的欧拉反褶积同时使用,以提高方法的解释能力.【期刊名称】《物探化探计算技术》【年(卷),期】2018(040)006【总页数】8页(P789-796)【关键词】位场;欧拉反褶积;叠加异常;垂向导数;反演效果【作者】罗潇;王彦国;张瑾;邓居智;吴姿颖;陈姝霓【作者单位】东华理工大学放射性地质与勘探技术国防重点学科实验室,南昌330013;东华理工大学放射性地质与勘探技术国防重点学科实验室,南昌 330013;东华理工大学放射性地质与勘探技术国防重点学科实验室,南昌 330013;东华理工大学放射性地质与勘探技术国防重点学科实验室,南昌 330013;东华理工大学放射性地质与勘探技术国防重点学科实验室,南昌 330013;东华理工大学放射性地质与勘探技术国防重点学科实验室,南昌 330013【正文语种】中文【中图分类】P631.20 引言重磁勘探具有经济、快速、范围大、探测深等优点,是进行大地构造划分、地质填图、矿产圈定等方面的重要方法[1-2]。

第二章反褶积反褶积是借助压缩基本地震子波来改善时间分辨率的一种处理过程。
为搞清这一过程要求综合研究正演问题,即必须首先研究记录的地震道的积木式分段单元。
地层是由不同类型岩性的岩层组成的,每种岩石类型都有地球物理学家所可利用的某种物理特性。
至于地震勘探,则根据波传播速度和岩层密度确定岩层。
密度与速度的乘积称之为地震波阻抗,地震资料分析期望的最终成果就是地震波阻抗剖面。
我们有在井中直接检测岩层速度和密度的方法,这种方法能向我们提供地震波阻抗与深度的关系。
在地面上沿测线记录到的地震反射波就是由于两地层之间的波阻抗差引起的。
记录到的反射记录可通过反射率与震源子波的褶积来模拟。
下面分别对褶积模型、各种反滤波进行介绍,并给出应用实例。
2.1褶积模型我们从图1给出的一个实际声测井记录入手,该声测井曲线是层速度与深度的关系图。
实际的速度测量是以2英尺的采样间隔在1000—5400英尺之间的深度段内完成的。
借助简单的斜坡把速度函数外延至地面。
该声测井记录显示出明显突变和强低频趋势特征,这两者构成了总的速度变化。
实际上我们通常用CM道集作速度分析进行估算的就是这种低频趋势。
对声测井曲线可通过人工分段提取其速度趋势,其结果可列表如下:由声测井记录确定的层速度趋势表1层速度深度范围地层序号(眺)(ft)1210001000 - -2000219000 探2000—22503187502250—25004126502500 - -37755196503775 - -5400探实际上该层速度是逐渐减小的。
我们所做的就是形成一组恒定层速度的层组。
把测井曲线进行这种分段多少有点类似于地质家对假想的地下模型所做的分层。
地质家是根据岩性分层,而我们根据声测井曲线的分段性质提取的分层则是以速度差为依据的。
下面对表1中所确定的地层的岩性分类:地层序号岩性1 灰岩2 泥质灰岩(泥岩含量逐渐增加)3 泥质灰岩4 泥岩5 白云岩在声测井曲线的低频趋势上附加有高频分量。

第二章反褶积反褶积是借助压缩基本地震子波来改善时间分辨率的一种处理过程。
为搞清这一过程要求综合研究正演问题,即必须首先研究记录的地震道的积木式分段单元。
地层是由不同类型岩性的岩层组成的,每种岩石类型都有地球物理学家所可利用的某种物理特性。
至于地震勘探,则根据波传播速度和岩层密度确定岩层。
密度与速度的乘积称之为地震波阻抗,地震资料分析期望的最终成果就是地震波阻抗剖面。
我们有在井中直接检测岩层速度和密度的方法,这种方法能向我们提供地震波阻抗与深度的关系。
在地面上沿测线记录到的地震反射波就是由于两地层之间的波阻抗差引起的。
记录到的反射记录可通过反射率与震源子波的褶积来模拟。
下面分别对褶积模型、各种反滤波进行介绍,并给出应用实例。
2.1 褶积模型我们从图1给出的一个实际声测井记录入手,该声测井曲线是层速度与深度的关系图。
实际的速度测量是以 2英尺的采样间隔在1000-5400英尺之间的深度段内完成的。
借助简单的斜坡把速度函数外延至地面。
该声测井记录显示出明显突变和强低频趋势特征,这两者构成了总的速度变化。
实际上我们通常用CMP道集作速度分析进行估算的就是这种低频趋势。
对声测井曲线可通过人工分段提取其速度趋势,其结果可列表如下:由声测井记录确定的层速度趋势表1地层序号层速度(ft/s)深度范围(ft)1 21000 1000—20002 19000 ※2000—22503 18750 2250—25004 12650 2500—37755 19650 3775—5400※实际上该层速度是逐渐减小的。
我们所做的就是形成一组恒定层速度的层组。
把测井曲线进行这种分段多少有点类似于地质家对假想的地下模型所做的分层。
地质家是根据岩性分层,而我们根据声测井曲线的分段性质提取的分层则是以速度差为依据的。
下面对表1中所确定的地层的岩性分类:地层序号岩性1 2 3 灰岩泥质灰岩(泥岩含量逐渐增加) 泥质灰岩4 5 泥岩白云岩在声测井曲线的低频趋势上附加有高频分量。
傅里叶反褶积算法简介傅里叶反褶积算法(Fourier Deconvolution)是一种在信号处理领域广泛应用的算法。
它主要用于恢复被模糊的信号,通过对信号进行傅里叶变换和逆变换,消除模糊效果,使得信号恢复清晰。
在实际应用中,由于各种原因(如传感器限制、噪声干扰等),信号往往会被模糊处理,这就给信号的分析和识别带来了困难。
傅里叶反褶积算法可以有效地解决这个问题,并广泛应用于图像处理、声音处理、通信系统等领域。
原理傅里叶反褶积算法基于傅里叶变换的思想。
傅里叶变换是将时域上的函数转换到频域上的函数,通过将函数表示为一系列正弦和余弦函数的和,可以更好地分析信号的频率成分。
具体而言,对于一个被模糊处理的信号f(t),我们可以通过以下步骤进行恢复:1.对信号f(t)进行傅里叶变换,得到频域上的函数F(ω)。
傅里叶变换将信号从时域转换到频域,使得我们可以更好地观察信号的频率成分。
2.对模糊核(Point Spread Function,PSF)进行傅里叶变换,得到频域上的函数H(ω)。
PSF描述了信号在传输过程中的模糊效果,通过对PSF进行傅里叶变换,可以得到其频率响应。
3.在频域上,将恢复的信号表示为G(ω)=F(ω)/H(ω),即原信号的频谱除以模糊核的频谱。
这样做的目的是消除模糊效果。
4.对G(ω)进行逆傅里叶变换,得到恢复后的信号g(t)。
通过以上步骤,我们可以将被模糊处理的信号恢复为清晰可见的信号。
算法流程1.输入被模糊处理的信号f(t)和PSF。
2.对f(t)进行傅里叶变换,得到F(ω)。
3.对PSF进行傅里叶变换,得到H(ω)。
4.计算G(ω)=F(ω)/H(ω),即原信号的频谱除以模糊核的频谱。
5.对G(ω)进行逆傅里叶变换,得到恢复后的信号g(t)。
应用领域傅里叶反褶积算法在许多领域都有广泛的应用,以下列举几个典型的应用领域:图像处理图像处理是傅里叶反褶积算法最常见的应用之一。
在图像处理中,由于传感器或者其他因素的限制,图像往往会产生模糊效果。
地震资料的处理方法和结果在很大程度上受野外采集参数的影响。
地震剖面的“三高”:高信噪比、高分辨率和高保真度。
地震资料处理主要有三个阶段;每一个阶段都是为了提高地震分辨率,即分离出两个无论在空间上还是时间上都非常相近的同相轴的能力。
●(a)反褶积是通过压缩基本地震子波成为尖脉冲并压制交混回响,沿着时间方向提高时间分辨率;●(b)叠加是沿着偏移距方向压缩,把地震资料的数据量压缩成零偏移距剖面,以提高信噪比;●(c)偏移是一个使绕射收敛,并将叠加剖面上的倾斜同相轴归到它们地下的真实位置上,通常在叠加剖面(接近于零偏移距剖面)上做偏移,来提高横向分辨率。
●几何扩散校正:通过给数据加一增益恢复函数以校正波前(球面)扩散对振幅的影响。
●建立野外观测系统:把所有道的炮点和接收点位置坐标等测量信息都储存于道头中以保证各道的正确叠加。
●野外静校正:对陆上资料,把所有炮点和接收点位置均校正到一个公共基准面上以消除高程、低降速带和井深对旅行时的影响。
关于分辩率的讨论:有一种普遍的误解,认为要增加时间分辨率只需要高频,这是不真实的。
只有低频或只有高频不能改善时间分辨率。
要增加时间分辨率低频和高频两者都需要。
时间分辨率取决于有效信号的频带宽度.最小平方法---根据误差的平方和最小来设计滤波器;最小相位信号是具有对相同振幅谱的物理可实现信号中相位最小的信号,或者说能量延迟最小的信号。
最小相位滤波器是具有同样振幅响应的一切可能的滤波器簇中能量延迟最小的滤波器,也称最小延迟滤波器。
若最小相位滤波器的输入是最小相位,则其输出也是最小相位,对于地震子波,除了零相位子波外,最小相位子波的分辨率最高。
下面的四个子波中哪一个是最小相位的:子波A :(4,0,-1) 子波B :(2,3,-2)子波C :(-2,3,2) 子波D :(-1,0,4)频率、视波数和视速度的关系为:**=k fV理想滤波器的滤波因子应为无穷序列,而数字滤波因子只能取有限个值。
反褶积的一大作用是压缩子波来提高分辨率,另一作用是统一子波及压制交混回响,使得波组特征更加清晰。
通过试验,本次处理使用了三个反褶积(如图十九为反褶积后的叠加剖面效果对比),在完成单炮去噪和一次剩余静校正后使用地表一致性反褶积,主要目的就是统一子波,尽可能地消除由于各种因素引起的子波不一致的现象,使得叠加达到更好的效果;然后在二次剩余静校正后做两步法反褶积,通过在炮集上预测子波,从而改善子波形态,同时也消除部分交混回响,叠加剖面的波组特征更为清晰;第三次反褶积在叠加剖面上做预测反褶积,使得剖面的面貌更为清秀,波组特征更为清晰。
至此已经基本解决了反褶积能解决的问题,也达到比较理想的效果。
1、叠后去噪试验
叠后去噪是在叠加剖面上去除一些随机干扰,提高剖面的信噪比,做好叠后去噪的试验也是相当重要的,要保证能提高信噪比,又不会因去噪过度而产生假分辨率。
本次处理试验验利用grisys的叠后去噪优势,充分组合试验各有用的去噪模块和参数,以达到理想的去噪效果。
如图十九是叠后去噪前后的对比,去噪后提高了信噪比却不失真,是通过多次试验对比后所采用的去噪方法。
实验二:观测系统的定义预处理与反褶积一、实验目的了解观测系统定义,会用模块解决原始资料中的废炮道、能量不均一及面波等噪音问题。
会试验反褶积模块和参数,能够输出经预处理与反褶积后的地震数据。
二、实验内容一)、原始资料导入(input)原始资料的路径图1 原始数据导入以第一炮为例图2 示例选择图中圆圈中的按钮,点击某一道,可以显示该道信息。
如图2所示选择第31道(chan)。
可以由数据导入知道,该每一炮的地震记录共120道,数据资料为275炮的地震记录,;道头长度184;采样频率为2.0ms。
还可以选择dx/dt,在图中鼠标中键可以观察地震资料中直达波是直线,反射波是双曲线,右键可以显示地震波在地层中的速度,如图3。
图3二)、切除、顶切和底切1、切除图4切除点击Picking-----Kill traces…打开一个对话框,输入列表名应用后选择切除道即CHAN,OK即可进行某一道或者几道的切除。
鼠标单击要切除的道,然后单击左侧刷子样的图标。
示例如图5。
切除了41、51和61道。
图5 切除2、顶切点击Picking-----Pick Top Mute…打开一个对话框输入列表名应用后选择aoffset,应用,在图上按住左键拖动选择,然后单击刷子的图标就能把所画线的上部切除。
如图6、7。
顶切底切图6 顶切和底切图7顶切注意图6中粗线以上的部分被完全切除。
3、底切点击Picking-----Pick Bottom Mute…打开一个对话框输入列表名应用后选择aoffset,应用,在图上按住左键拖动选择,然后单击刷子的图标就能把所画线的上部切除。
如图6、8。
图8 底切注意图8中粗线以下部分被完全切除。
在地震资料处理中,切除、底切、顶切很少使用,毕竟地震资料来之不易,而且资料珍贵,不容有部分缺失。
三)、二维海上观测系统定义(2D Marine Geometry)1、在ProMax中选择二维海上观测系统定义2D Marine Geometry Spreadsheet*,运行后进行参数等的设定。
反褶积是通过压缩地震记录中的基本地震子波,压制交混回响和短周期多次波,从而提
高时间分辨率,再现地下地层的反射系数。反褶积通常应用于叠前资料,也可广泛用于叠后
资料。反褶积得到具有更高时间分辨率的剖面。反褶积的作用有时不局限在压缩子波上,它
也能从记录上消除大部分的多次波能量。
在地震勘探中,岩石层由密度和地震波传播速度定义。密度和速度的乘积称为地震波阻
抗。相邻岩石层之间的波阻抗差形成反射后,由沿地表的测线所记录。这样得到的地震记录
可表示为一个褶积模型,即地层脉冲响应与地震子波的褶积。子波有许多成分,包括震源信
号、记录滤波器、地表反射和检波器响应等。地层脉冲响应是当子波为一个尖脉冲时所记录
的。理想的反褶积应该压缩子波并消除多次波,在地震道内只留下地层反射系数。
反褶积是通过压缩基本地震子波以提高地震资料的时间分辨率的过程,它既可用于叠前,
也可用于叠加资料。反褶积方法都基于地震波的传播过程是一个线性系统,符合褶积模型,
即地震数据是由震源子波和地层反射系数序列的褶积,加上一些随机噪声组成的。反射系数
序列本身具有足够的分辨率,我们只要去掉子波的影响,就能达到提高数据纵向分辨率的目
的。反褶积除了压缩子波外,还能从剖面上消除大部分的多次波能量。
反褶积的原理如下:
根据上述目的可以知道,反褶积基本原理可用图1来说明。
现在我们通过褶职模型公式(3-3)来说明如何实现这个目的。先假设不存在干扰波n (t),
即:
ttbtStx
对两边求傅氏变换,则得到频率域的地震记录表示式:
BX (1)
式中,X、B和分别为地震记录频谱、子波频谱和反射系数的频谱。
显然:
XB
1
(2)
如果令:
B
A1
(3)
则有:
XA (4)
再作傅氏反变换变至时间域,就可得到:
ttbtatxtat
(5)
式中,a(t)为A的时间函数。
根据(5)式知:
ttbta
因为b(t)为地震子波,而a(t)和b(t)之间又存在着频谱互为倒数的关系(即
BA/1
),所以把a(t)称为反子波,又叫做反褶积因子。
由此可知,如已知地震子波,利用数学方法求出a(t),再利用(3-8)式让反子波
a(t)
与地震记录x(t)作褶积,就可以求出反射系数序列t:
txat (6)
这样一个过程就叫做反褶积(或反滤波)。经过这样的处理,就可以达到把地震子波压缩
成尖脉冲,从而达到提高地震记录纵向分辨能力的目的。
为什么把这样一个褶积运算(其物理实质是一种滤波)的过程叫做反褶积(或反滤波)呢
把上述过程用图表示出来,大家就很清楚了。
由图2可知,反褶积仍然是一个滤波过程,不过由于这种滤波过程的作用恰好与某个
滤波过程的作用相反,因此才被叫做反滤波(而由于这里的滤波和反滤波在数学上都可以通
过褶积运算来完成,所以又可把后者叫做反褶积)。
图1 反褶积原理原理图
图2 反滤波过程示意图
由于反褶积实质上仍是一种滤波,所以我们在第一章数字滤波中学过的一些内容在这里
仍是有用的,即反褶积的计算仍可通过时域褶积或频域乘积来实现,它也可以放在叠加前进
行,也可以在叠加后实施。但应注意的是,滤波和反褶积在地震资料处理中的目的是不同的,
前者是为了提高信噪比,后者则主要是为了提高分辨率。
由上面的叙述知道,研究反褶积就是研究如何设计一个(反)滤波器以抵消大地滤波器
(包括地震记录中各种装备如检波器、记录仪器等对地震子波的滤波作用)的作用。通常有两
种方法来设计反滤波器:确定性方法和统计方法,也就是可以将反褶积分为确定性反褶积和
预测反褶积。由BA/1变换到Z变换域,有zBzA/1。该式可以作为确定地震勘
探中的反滤波因子的一个十分简单的代数方法的依据。但这中间存在两个问题:①求
A(z)
必须知道B(z),也就是说必须已知地震子波b(t)(或大地滤波因子b(t)),而这在地震勘探
中有时是很难做到的(特别是对陆上勘探炸药震源情况下);②由于ta一般情况下应是一无
穷序列(因为tb有限,所以B(z)为有限项多项式,其倒数A(z)则为无穷级数,而其系数构
成的a(t)则是无限长序列了),实际处理中仅能取有限项,所以只能近似地确定a(t),如何
近似可以有不同的方法。由此可知,确定性反滤波当①不能满足时是无法实现的,而当近似
截取时取得不妥当时,效果不会太好。所以,地震勘探中往往是利用统计的方法来求取最佳
反褶积因子的(某种条件下的最佳)。
反褶积在提高纵向分辨率的同时,往往会降低信噪比。这从频率域上讨论比较方便。理
想反褶积的输入为地震记录,输出为白噪反射序列。从频率域上说就是将地震记录的谱变为
幅值近似相等的白噪的谱。这样,如果记录上的干扰噪音没有消除干净,则残留的干扰会同
时得到放大,于是降低了信噪比。因此,在进行反褶积之前应当经过比较彻底的滤波处理以
最大限度地压制干扰,在反滤波之后还需进行宽档滤波以提高信噪比。发展同时提高信噪比
和分辨率的特殊处理方法,首先必须发展可以识别有效波或能区分有效波和干扰的特殊处理
方法,否则是不现实的。
在地震数据处理中,反褶积是用来提高分辨率的必要手段,但同时往往会降低资料的信
噪比。当地震资料不满足最小相位和白噪声约束条件时,常规的反褶积方法也将不再适用。
反卷积技术是广义的地震反演的一部分;严格的反演是要提取地震参数,而反褶积企图提取
反射系数,实际只能压缩子波。提高纵向分辨率是数据处理的一个主要任务,也是反褶积方
法的主要用途。
假设带来的问题:
各种常规反褶积方法都必须有一定的假设条件,而在实际工作中有些条件又是不可实现
的,限制了反褶积方法的应用。反射地震记录的褶积模型不可靠。褶积模型中的地震子波是
大地滤波器的脉冲响应,然而,大地滤波的作用十分复杂,所以,为了发展提高分辨率的反
滤波方法,应努力研究大地滤波的机制。反褶积在提高纵向分辨率的同时,往往会降低信噪
比,提高记录噪声水平,给信号的提取带来困难。传统的反褶积方法需要先做振幅补偿,再
做反褶积,其中在做振幅补偿时存在补偿误差,因此在其之上做的反褶积存在误差累计,导
致效果不佳。各种反褶积方法的前提大多是地震子波已知,而实际恰恰相反。因此,反滤波
发展的另一个方向是子波提取技术。
改进的方法:
混合相位未知脉冲的最小平方反褶积。混合相位未知脉冲的最小平方反褶积是一种多次
迭代方法,它把混合相位未知脉冲的最小平方反褶积和一种最小熵类型的脉冲成形技术结合
在一起,用来改进有限长度混合相位未知子波的反褶积效果。
多分辨率地震信号反褶积。地震信号各频段都包含反射系数的信息,只不过较低频段包
含的信息与高频段相比其分辨率较低。但是,由于低频段的信噪比往往比高频段高,如果能
够从低频段提取反射系数信息,则所提取的信息受噪声干扰将相对要少。这一特性使我们可
以对地震信号进行分频段反褶积处理,并依次以具有较高信噪比的低频段的反褶积结果对高
频段的反褶积结果进行预测或修正,从而消除测量噪声对反褶积的影响,提高反褶积处理的
精度。神经网络子波反褶积。常用的求反子波方法得到的反子波与子波褶积后输出并不接近
一个尖脉冲,而往往有过多且过大的旁瓣存在。可以利用超级多道振幅谱平均求取子波振幅
谱,用常相位校正估计子波相位,得到一估计子波。反子波的求取不是直接利用估计子波,
而是利用神经网络技术,即根据子波自动给出期望输出,然后利用此期望输出训练网络得到
反子波。