反褶积学习基础课件
- 格式:ppt
- 大小:1.74 MB
- 文档页数:109


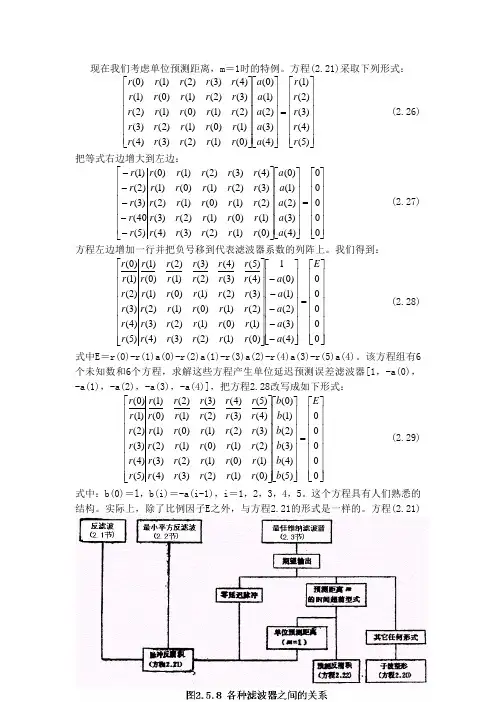
现在我们考虑单位预测距离,m =1时的特例。
方程(2.21)采取下列形式:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡)5()4()3()2()1()4()3()2()1()0()0()1()2()3()4()1()0()1()2()3()2()1()0()1()2()3()2()1()0()1()4()3()2()1()0(r r r r r a a a a a r r r r r r r r r r r r r r r r r r r r r r r r r (2.26) 把等式右边增大到左边: ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----00000)4()3()2()1()0()0()1()2()3()4()1()0()1()2()3()2()1()0()1()2()3()2()1()0()1()4()3()2()1()0()5(40()3()2()1(a a a a a r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r (2.27) 方程左边增加一行并把负号移到代表滤波器系数的列阵上。
我们得到: ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡00000)4()3()2()1()0(1)0()1()2()3()4()1()0()1()2()3()2()1()0()1()2()3()2()1()0()1()4()3()2()1()0()5()4()3()2()1()5()4()3()2()1()0(E a a a a a r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r (2.28) 式中E =r(0)-r(1)a(0)-r(2)a(1)-r(3)a(2)-r(4)a(3)-r(5)a(4)。

第二章 反褶积将地震记录看成是反射系数序列与地震子波的褶积,反褶积就是要消除这种褶积过程,从地震记录得到反射系数序列。
一般说来,反褶积的目的是消除某种已知的或未知的褶积过程的运算。
反褶积也可能用来消除震源信号或者记录仪器的响应。
反褶积也可能是用另一种褶积过程代替原来的褶积过程。
反褶积是一种滤波。
与一般滤波的区别有两点:一是着眼点在改变子波,而不是衰减噪声。
二是方法上是根据需要达到的目标由地震资料自动推导滤波器,而不是通过试验选择滤波器。
反褶积是子波级的处理,是常规处理中最精细的环节。
一 子波与反褶积原始记录上的子波不管如何千变万化,必然是单边子波。
可控震源原始记录上的子波也是单边的,即扫描信号,经过相关以后才变成双边子波。
单边子波是物理可实现的,双边子波是非物理可实现的。
单边子波可以是最小相位子波、最大相位子波或混合相位子波。
判别方法可以有很多,对于下面的讨论来说,用Z 变换大概是最方便的。
将子波的各个样点值作为系数、样点序号作为Z 的幂次,写成Z 多项式,如果Z 多项式的根的模全部大于1,即根全部在单位圆外,就是最小相位子波;如果Z 多项式的根全部在单位圆内,就是最大相位子波;如果Z 多项式的根有一些在单位圆外,有一些在单位圆内,就是混合相位子波。
Z 多项式可以因式分解,每个因式有01=+bZ 形式,它代表有一个根Z 1-=。
(b 可以是实数,也可以是复数。
如是复数,必然共轭成对出现。
)可见当1<b 时,这个因式是最小相位的;当1>b 时,这个因式是最大相位的。
如果所有因式是最小相位的,子波就是最小相位的;如果所有因式是最大相位的,子波就是最大相位的;如果有一部分因式是最小相位的,有一部分因式是最大相位的,子波就是混合相位的。
因此,最小相位子波的尾点的绝对值必然小于其首点的绝对值,最大相位子波的尾点的绝对值必然大于其首点的绝对值,混合相位子波则可以是任何情形。
根据这个简单规则,至少在看到尾点的绝对值大于首点的绝对值的子波时,立刻就能判断它绝对不可能是最小相位子波。




反褶积处理方法论文提要反褶积即反滤波是常用的地震资料处理方法。
反褶积的目的是由地震数据恢复反射系数。
反滤波的作用主要是压缩地震反射脉冲的长度,提高反射地震记录的分辨能力,并进一步估计地下反射界面的反射系数。
这不仅是常规地震资料处理所需要的,而且是对直接找油找气的亮点技术和岩性研究的地层地震学的地震资料处理尤为重要。
另外,反滤波还可以清除短周期鸣震和多次波等干扰波。
当前地震资料处理解释已经基本实现了数据化、自动化,我国各大解释公司、研究所、高等院校都已有了较为先进数字化处理软件,在处理数字化的地震数据时表现出了很好的速度性和准确性。
反褶积可分为确定性反褶积和估计性反褶积两种。
目前常用的反褶积有最小平方反褶积、预测反褶积、同态反褶积、地表一致性反褶积、最大熵反褶积、变模反褶积、Q反褶积等等;特殊的反褶积有Noah反褶积、最小信息反褶积等。
正文一、反褶积(一)研究目的和意义1、研究目的(1)弄清各种反褶积处理方法的原理。
(2)弄清反褶积处理模块的参数意义。
(3)掌握地震资料数字处理的基本流程及处理方法。
(4)完善反褶积方法,提高地震资料处理的分辨率,保持信噪比,振幅均匀化。
2、研究意义反褶积是地震资料数字处理流程中最关键的一环,也是提高地震勘探分辨率最有效的方法。
一个处理流程包括许多处理步骤。
而每一个处理步骤又要涉及到好几个处理模块。
一个处理流程通常由预处理、叠前处理和叠后处理三部分组成。
其中反褶积是最重要的一个部分,如图1所示。
反褶积的目的就是为了分离子波和反射系数序列。
子波就像无线电中的载波,反射系数序列就像无线电中的声波。
只有消除高频载波才能提取声波。
子波在地层中传播,携带着反射系数序列这种有用的地质信息返回地面,只有消除子波才能恢复反射系数序列的本来面目。
反射系数序列中有波阻抗随时间变化的信息,这就提供了速度和密度随时间变化的信息,随之就可得到地层、岩性及构造在地下中间分布的信息。
在有利条件下还可得到岩石孔隙率、渗透率、孔隙流体性质(油、气、水)乃至地层压力的信息。
复深层的较高频带资料。
图9(a)显示的是叠前脉冲反褶积剖面,图9(b)是叠前脉冲反褶积和叠后时变谱白化的处理结果。
显然。
后者与只作反褶积的剖面相比它包含着较高频率的信号。
通过另一种频率域方法可以获得展平的频谱。
如附录所讨论的那样,我们可以列出频率域最小相位脉冲反褶积公式。
除此之外,我们可以不涉及相位而只选择拉平的频谱。
这种情况可以称为零相位频率域反褶积。
这实质上等效于TVSW。
如果我们的目的只是拉平频谱,就可以取图10的处理方法,这个方法与图12中给出的频率域反褶积的表示形式是不同的。
图10中描述的频率域反褶积在某一方面与附录中描述的反褶积是不同的。
这个算子是在时间域设计的,并且在上述情况下应用在频率域中。
另一方面,在后面的情况中,设计的反褶积算子严格地应用在频率域中。
显然算子的域可能是不同的。
但最小相位频率域反褶积和维纳-莱文森反褶积技术都应获得同样的效果。
对比图1和图8说明频率域方法有产生一些噪音的趋势,这是与谱计算中的舍入误差有关。
频率域处理方法的优点是提供作只拉平频谱零相位运算的机会。
正如我们先前阐明的,这与TVSW等价。
频率域零相位反褶积是指TVSW要求把输入的地震记录分成许多小的时窗,并在各个时窗内计算和应用图10所描述的程序。
它有提供时变谱展平的能力,图8下图显示的是零相位频率域反褶积后的野外记录。
显然这个输入可与图8中的TVSW输出相比。
仅有叠前频率域反褶积和反褶积后又作了TVSW处理的剖面分别显示在图11(a),图11(b)中,这些结果可以分别与只有脉冲反褶积(维纳-莱文森)的输出结果及脉冲反褶积后又作TVSW处理的结果相比较〔见图9(a),(b)〕。
结论反褶积是指把非弹性地层转化为弹性地层。
脉冲震源的大地响应转换成子波,随着它向地下传播过程以不稳定方式使子波的振幅和相位不断地变化。
由于球面扩散使振幅衰减,甚至在均匀介质中也是如此。
子波变宽是由于岩层固有的吸收作用使其高频成分损失所致。

第七章用好反褶积的重要性第一节单道反褶积的坏处在地震资料处理流程中比较重要的一步是作反褶积,常规使用的有脉冲反褶积、预测反褶积及零相位反褶积三种。
长久以来,大家一直在使用单道上运算的反褶积,没有想到它是高分辨率的大敌。
我做了一个实际资料的试验。
图60是野外一张单炮记录在反褶积前的一段波形,从0.8s 至2.0s定为反褶积时窗。
采样率为2ms。
此段记录中间有较强的面波,炮点在第80道。
左方在面波范围以外可以见到有些反射同相轴,如箭头所指。
将此段记录作脉冲反褶积,使用常规的千分之一白噪系数,得到结果如图61。
此图中面波被反褶积所压制,似乎不错。
但是有效反射波却受到了损害,如左方1.15s处的反射同相轴上下抖动,套得很不好。
研究其所以然,且看图62。
图62(b)是对应于各道的自相关函数,可以看到凡是原始记录上面波很强的道,如79及81、83等,其自相关波形发胖,振幅很强。
而左方第63道附近自相关波形瘦而弱。
大家知道反褶积因子是由地震道的自相关函数所决定的,所以图62(a)所列的各道的反褶积因子就各异。
凡是自相关发胖的地方,反褶积因子就瘦而尖锐;而自相关瘦的道,它的反褶积因子就相对的发胖。
于是整张记录各个道就等于分别用了不同的滤淀因子来做滤波。
其后果是各道的真正的反射子波被改造了,而且改乱了,以后还无法弥补,因为它的相位谱也已经改乱了。
我接着对这张记录做多道统计的脉冲反褶积。
即将各道的自相关函数相加平均,求得一个统计平均自相关函数,然后求反褶积因子,将此反褶积因子作用于所有的道,就得到如图63的结果。
这个多道反褶积的效果就很好,特别是左方各反射波排得很整齐,如箭头所指。
1.lOs处的一个反射可以贯穿整张记录进行追踪。
显然,效果比单道反褶积(图61)为好。
当然,由于这次统计反褶积在中央部分并不是专门针对压面波的,所以面波的遗留振幅稍微多一些,不过无伤大雅。
我们宁可要一个各道统一的子波改造,也不能要许多个改造乱了的子波。

论反褶积的概念及类型论文提要地震勘探技术在油气田勘探开发中起着重要作用。
地震勘探包括地震采集、处理和解释三大部分。
地震采集是利用野外地震采集系统获取地震数据处理所需的反射波数据;地震数据处理的目的是对地震采集数据做各种处理提高反射波数据的信噪比、分辨率和保真度以便于解释;地震解释分为构造和岩性解释,目的是确定地震反射波数据的地质特征和意义。
地震数据处理依赖于地震采集数据的质量,处理结果直接影响解释的正确性和精确度。
探讨地震处理的基本原理和基本方法有助于全面利用采集数据,充分利用处理方法,为地震解释提供可靠的处理成果剖面。
正文地震数据处理主要包括地震反褶积、叠加和偏移成像三大技术。
地震反褶积是通过压缩地震子波提高地震时间分辨率;叠加的目的是压制随机噪声提高地震信噪比;偏移成像包括射线偏移和波动方程偏移两大类,主要目的是实现反射界面的空间归位和恢复反射界面空间的波场特征、振幅变化和反射系数,提高地震空间分辨率和地震保真度。
反褶积是地震资料最常用和最重要的处理方法之一。
反褶积可在叠前做也可在叠后做。
叠前反褶积的目的是把地震子波压缩成尖脉冲来改进时间分辨率。
叠后的预测反褶积主要是消除海上鸣震(交混回响)等多次波干扰,突出有效波,提高地震资料的信噪比。
在常规处理中反褶积的基础是最佳维纳滤波。
反褶积后要用某种类型的道均衡,以使数据达到通常的均方根振幅水平。
一、反褶积的概念(一)反褶积问题的提出实际地震记录由于受复杂子波的作用和干扰的影响,分辨能力较低,地质界面上各反射波互相叠加、彼此干涉,成为一复杂的形式,不能通过地质资料的解释,得到准确的地质界面。
反褶积的目的就是要通过某种数学方法,压缩地震子波,使地震记录分辨率提高,从而近似反射系数剖面,得到地下介质精确的反射结构。
假定地震记录不含干扰,何以得到x(t)=b(t)*ξ(t) (1-1)对应的频率域形式X(ω)=B(ω)×Ξ(ω)(1-2)令A(ω)=1/ B(ω)(1-3)则可得到Ξ(ω)= A(ω)×X(ω)(1-4)写成时间域形式ξ(t)=a(t)* x(t)(1-5)由x(t)=b(t)* ξ(t) 和ξ(t)=a(t)* x(t)可以看到:前者由子波和反射系数得到地震记录,是一褶积过程;后者则反过来,由一函数与地震记录褶积得到反射系数,这一过程可被称为反褶积。
论反褶积的方法及作用论文提要反褶积是地震资料最常用和最重要的处理方法之一,它可用于叠前,也可用于叠后。
反褶积的主要作用是压缩地震子波、提高地震资料的分辨率,从而提高地震资料的解释精度。
为油田精细勘探和开发服务。
另外,反褶积还可以消除短周期鸣震和其他多次波干扰,突出有效波,提高地震资料的信躁比。
反褶积的主要方法有:最小平方反褶积、预测反褶积、子波提取与子波整行反褶积、同态反褶积、地表一致性反褶积等。
做反褶积是为了得到一个反射系数序列,反射系数可以反映层的位置、层的反射能力及层之间差异。
总之,反褶积的目的是通过某种数学方法使地震纪录的分辨率提高从而近似放射系数剖面得到地下精确的反结构。
正文一、反褶积的概念(一)理想模型若地震波以脉冲形式激发经过地层时无吸收、透射和多次反射等因素的影响,而且整个过程不存在随即干扰,这样就可以得到理想的输出:x(t)=bδ(t)*ξ(t)=bξ(t)这时得到的输出实际上就是反射系数序列,做反褶积就是为了得到它,为了讨论问题方便起见,我们先假定不含干扰波,由此我们可以从以上的式子中得到x(t)=b(t)*ξ(t)设计反滤波因子a(t),在时间域上a(t)是b(t)的逆,即有:a(t)*x(t)=ξ(t)(二)实际地震纪录实际地震纪录x(t)由有效波s(t)和干扰波n(t)组成:x(t)=s(t)+n(t)有效波是指一次反射波,对反射波地震看探而言,除一次反射波以外的一切波都是干扰波,一次反射波可以用以下褶积模型表示:s(t)=b(t)*ξ(t)b(t)称为地震子波;§(t)称为反射系数序列。
严格意义上讲,地震子波同震源子波o(t)概念还是有区别的:b(t)=o(t)*g(t)*τ(t)*d(t)*i(t)=a(t)*f g(t)*f d(t)式中:g(t)-------地层响应τ(t)--------透射响应d(t)--------地面接收响应 i(t)---------仪器响应()t f g = g(t)* τ(t) (大地滤波器)()t f d = d(t)*i(t) (接收滤波器)式中干扰波并不是单单的随机干扰,有非激发干扰()t n 0、背景噪声()t n 1及规则干扰N(t)叠加而成:n(t)= ()t n 0 + ()t n 1+ N(t)规则干扰分为两类:一类与地质结构有关,包括多次波、转换波、断面波、绕射波、伴随波、折射波、瑞利波、勒夫波和斯通利波等,这类波在特定的条件下可能转化为有效波;另一类与地质结构无关,如水中鸣震、气泡效应、地表及海面散射等。