RLS和LMS自适应算法分析资料

回声消除几种常用的算法比较（1）LMS与RLS自适应滤波算法性能比较最小均方(LMS, Least Mean Squares)和递推最小二乘(RLS, Recursive Least Squares)两种基本自适应算法进行了算法原理、算法性能分析。

计算机模拟仿真结果表明，这两种算法都能通过有效抑制各种干扰来提高强噪声背景中的信号。

检测特性相比之下，RLS算法具有良好的收敛性能，除收敛速度快于LMS 算法和NLMS算法以及稳定性强外，而且具有更高的起始收敛速率、更小的权噪声和更大的抑噪能力。

基于自适应噪声抵消系统，对比研究了两类自适应滤波算法在噪声抵消应用中的滤波性能。

计算机仿真实验结果表明，两种算法都能从高背景噪声中提取有用信号。

相比之下，RLS算法具有比LMS好得多的启动速度和收敛速度，对非平稳信号适应性强，其滤波性能明显好于LMS算法，但其计算复杂度高，不便于实时处理。

而LMS算法相对存在收敛速度不够快和抵抗突出值干扰能力不够强。

值得深入研究的是降低RLS算法的计算复杂度，进一步提高LMS算法的收敛速度并减少其残余(失调)误差。

(2)LMS与NLMS的比较通过理论分析和实验对比得出NLMS算法的复杂度最小且鲁棒性最好，但是遇到相关信号时，收敛速率最慢。

在实际应用中，NLMS算法便可以基本满足要求，但是NLMS算法步长选择一种收敛速度和收敛精度的折衷。

(3) NLMS算法与NBLMS算法的比较由于回声消除的效果除了与算法有关外，还与滤波器系数的个数、采样率、削波处理、近端语音信号检测等因素相关，因此对两个算法进行比较时，这些因素都取相同值．两种算法在代码大小和所需指令周期上的比较两种算法在代码大小和所需指令周期上的比较见表1．由此可见：两种算法在性能上的差异与滤波器系数的个数N 和滤波器系数块大小M有关．上述的几种算法各有特点。

(1)RLS算法即使是在输入信号相关矩阵的特征值扩展比较大的情况都能实现快速收敛，且对输入参考信号特征值散布不敏感，但其实现都以增加计算复杂度和稳定性问题为代价，而这些问题对于基于LMS准则的算法来说却并不重要，因此实际应用中很少采用。

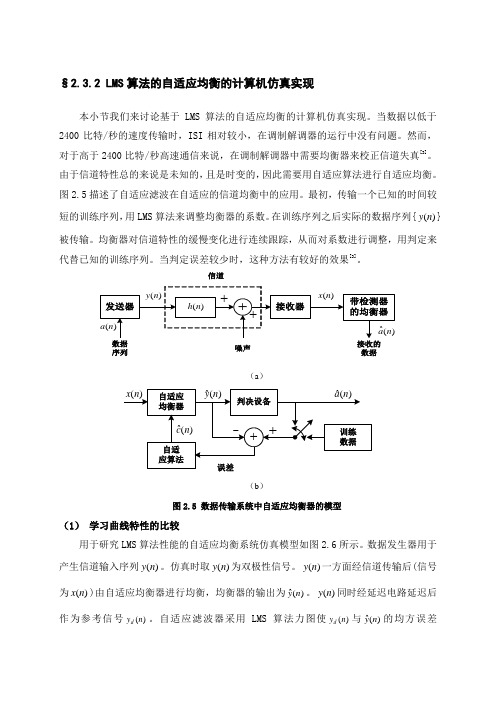
§2.3.2 LMS 算法的自适应均衡的计算机仿真实现本小节我们来讨论基于LMS 算法的自适应均衡的计算机仿真实现。

当数据以低于2400比特/秒的速度传输时，ISI 相对较小，在调制解调器的运行中没有问题。

然而，对于高于2400比特/秒高速通信来说，在调制解调器中需要均衡器来校正信道失真[3]。

由于信道特性总的来说是未知的，且是时变的，因此需要用自适应算法进行自适应均衡。

图2.5描述了自适应滤波在自适应的信道均衡中的应用。

最初，传输一个已知的时间较短的训练序列，用LMS 算法来调整均衡器的系数。

在训练序列之后实际的数据序列{)(n y }被传输。

均衡器对信道特性的缓慢变化进行连续跟踪，从而对系数进行调整，用判定来代替已知的训练序列。

当判定误差较少时，这种方法有较好的效果[3]。

信道（a ）（b ）图2.5 数据传输系统中自适应均衡器的模型（1） 学习曲线特性的比较用于研究LMS 算法性能的自适应均衡系统仿真模型如图2.6所示。

数据发生器用于产生信道输入序列()y n 。

仿真时取()y n 为双极性信号。

()y n 一方面经信道传输后(信号为)(n x )由自适应均衡器进行均衡，均衡器的输出为)(ˆn y。

()y n 同时经延迟电路延迟后作为参考信号()d y n 。

自适应滤波器采用LMS 算法力图使()d y n 与)(ˆn y的均方误差2{|()|}E e n 取最小。

数据发生器信道延迟D自适应均衡器噪声发生器LMS ()h n ()()d y n y n D =-()x n ()y n ()v n ++()c n ()e n ()y n ()s n图2.6 研究自适应均衡器性能的系统仿真框图仿真时，信道采用升余弦脉冲响应来模拟[3][7]：20.51cos (2)1,2,30()n n W h n π+-==⎧⎧⎫⎡⎤⎪⎨⎬⎢⎥⎨⎣⎦⎩⎭⎪⎩其他 (2.3.14)该脉冲响应关于2=n 对称。

自适应滤波器(分别采用LMS 和RLS 算法)对IIR 系统辨识1. LMS 和RLS 算法简介LMS 自适应滤波算法是以均方误差最小为准则的，其意义是是滤波器的输出信号和需要信号的误差平方的统计平均值最小，这个准则是依据输入数据的长期统计特性寻求最佳滤波的。

而最小二乘（RLS ）算法是只依据一组数据来寻求最佳滤波的方法。

因此，LMS 滤波是统计意义上的最佳滤波器，而RLS 滤波是针对不同的数据组生成不同的最佳滤波器。

RLS 算法实际上是FIR 维纳滤波器的一种时间递归算法，它是严格以最小二乘方准则为依据的算法。

它的主要优点是收敛速度快，因此，首先在快速信道均衡，实时系统辨识和时间序列分析中得到广泛应用。

其主要缺点是每次迭代计算量很大(对于L 阶横向滤波器，计算量数量级为2L ），因此，在信号处理中它的应用曾一度收到限制。

但是近年来人们重新对它产生了兴趣，主要是因为它具有收敛速度快的优点。

RLS 算法的关键是用二乘方的时间平均的最小化准则取代最小均方准则，并按时间迭代计算。

具体来说，是要对初始时刻到当前时刻所有误差的平方进行平均并使其最小化，在按照这一准则确定FIR 滤波器的权系数矢量w ，即所依据的准则是20()()min nk n e k ε===∑ (1)其中()()()e k d k y k =-式中，()d k 是期望响应，()y k 是L 阶FIR 滤波器的输出相应，即()()()T T y k k k ==w x x w (2)2. 自适应滤波器系统辨识原理如下图所示为自适应滤波器辨识未知系统的基本结构图，其中未知系统可以使FIR 结构，也可以是IIR 结构。

在结构图中，x(n)为辨识系统而产生的输入信号，通常可以选择为白噪声，同时输入未知系统和自适应滤波器。

d(n)为未知系统的输出信号，即自适应滤波器的参考信号。

调整自适应滤波器的系数，使误差信号e(n)的均方误差达到最小，则自适应滤波器的输出y(n)近似等于未知系统的输出d(n)。

RLS 自适应算法分析及仿真RLS 自适应算法是为了设计自适应的横向滤波器把最小二乘法推广为一种自适应算法。

使得在已知n-1时刻横向滤波器抽头系数的情况吓，能够通过简单的更新，求出n 时刻的滤波器抽头权系数。

这样一种自适应的最小二乘法称为递推最小二乘法，简称RLS 算法。

RLS 自适应算法使用的确定性线性回归模型Kalman 滤波算法的一种特殊的无激励的状态空间模型。

一、RLS 算法步骤：步骤一：初始化：(0)0w =，1(0)P I δ-=，其中δ是一个很小的值。

步骤二：更新： n=1,2,……()()(1)()H e n d n w n u n =--(1)()()()(1)()H P n u n k n u n P n u n λ-=+- 1()[(1)()()(1)]H P n P n k n u n P n λ=---*()(1)()()w n w n k n e n =-+其中，11(0)(0)P R I δ--==，δ是一个很小的正数。

二、仿真结果：从上图可以看出RLS滤波的跟踪性能是比较好的，滤波器的输入与输出在初始值之后几乎重合。

由于RLS存在自适应更新过程，因此其效果比LMS更好。

由下图可以看出，其RLS算法误差是具有收敛性的，收敛结果与δ密切相关，δ在取值为1的时候严重影响RLS算法的收敛速度及结果。

三、仿真程序：clear allclcM=5;%权系数个数N=100;%数据点数n=1:N;wn=0.36*randn(1,N);vn=randn(1,N);d(1)=0;for n=2:Nd(n)=0.8*d(n-1)+wn(n); %期望响应enduu=d+vn;w=zeros(M,1);P=0.05*eye(M,M);q=0.1; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%for n=M:N;u=uu(n:-1:n-M+1)' ;e(n)=d(n)-w'*u;k=P*u*inv(q+u'*P*u);P=(1/q)*(P-k*u'*P);w=w+k*e(n);out(n)=w'*u;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%subplot(211)t=1:N;hold on;plot(d(t));hold on;plot(out(t),'r');grid onlegend('滤波器输入','滤波器输出')subplot(212)semilogy(abs(out-d));title('误差值')。

自适应均衡实验1、实验内容和目的1）通过对RLS 算法的仿真，验证算法的性能，更加深刻的理解算法的理论。

2）分别用RLS 算法和LSM 算法实现图1中的自适应均衡器，比较两种算法的差异，分析比较算法的性能，从而掌握两种算法的应用。

图1 自适应均衡框图2、基本原理分析1）LMS 算法原理LMS 算法一般来说包括两个基本过程：滤波过程和自适应过程。

滤波过程来计算线性滤波器的输出及输出结果与期望响应的误差。

自适应则是利用误差来自动调节滤波器的参数。

LMS 算法也是一个递推的算法。

设()J n 是滤波器在n 时刻产生的均方误差，其梯度计算如下：()()22n n ∇=-+J p Rw其中R 和p 分别是输入的自相关矩阵和输入与期望输出的互相关矩阵：()()()ˆH n n n =Ru u()()()*ˆn n n =pu d 则梯度向量的瞬态估计为：()()()()()()*ˆˆ22H n n n n n n ∇=-+J u d u u w 由最速下降算法可以得到抽头向量更新的递推关系式：()()()()()()*ˆˆˆ1Hn n n n n n μ⎡⎤+=+-⎣⎦w w u d u w整个LMS 算法归纳总结如下： 参数设置：M=抽头数（滤波器长度） μ=步长参数 m a x20MS μ<<其中max S 是抽头输入功率谱密度的最大值，而滤波器长度M 为中到大 初始化：如果知道抽头权向量()n w 的先验知识，则用它来选择()ˆ0w 的合适值，否则令()ˆ00=w。

更新滤波过程：()()()ˆH y n n n =wu ()()()e n d n y n =- ()()()()*ˆˆ1n n n e n μ+=+ww u 2）RLS 算法原理RLS 算法是一个递归的过程，递归最小二乘问题的正则方程可用矩阵写为()()()ˆn n n =Φwz 其中n 是可测数据的可变长度，()n Φ更新抽头输入的自相关矩阵，()n z 是抽头输入与期望响应之间的互相关向量，()ˆn w 是抽头的权值向量。

LMS和RLS算法应用及仿真分析
LMS算法（Least Mean Squares）是一种基于梯度下降策略的机器学
习算法，它主要应用于解决系统辨识、信号分类和数据拟合等问题。

LMS
算法是一种收敛率较高的优化算法，由于其算法简单、快速，因此在工业
中被广泛应用。

基本原理：LMS算法的基本原理是进行参数更新，以最小化残差平方
和（RSS）作为目标函数，从而改善结果的稳定性和准确性。

LMS算法的
另一个重要思想是，在学习过程中每次迭代都仅使用当前一个输入和相应
的输出。

因此，该算法不需要获得训练样本数据的完整集合，可以仅仅从
一个训练样本中获得有限的信息，并通过这种限定的信息进行迭代。

LMS算法的算法步骤：
（1）初始化参数θ；
（2）给定一个输入样本xn，根据当前的参数θ计算出预测输出ŷn；
（3）根据已知的真实输出dn，计算出当前的残差en；
（4）根据梯度下降法更新参数θ；
（5）重复2～4步，直到达到目标函数的收敛性。

仿真分析：
首先，使用Matlab仿真模拟LMS算法，以模拟实际的系统辨识任务。

第三章 递归最小二乘(RLS)自适应均衡算法§3.1 引言在自适应滤波系统中，最陡梯度(LMS )法由于其简单获得了广泛的应用。

但各种LMS 算法均有收敛速度较慢(收敛所需码元数多)，对非平稳信号的适应性差(且其中有些调整延时较大)的缺点。

究其原因主要是LMS 算法只是用以各时刻的抽头参量等作该时刻数据块估计时平方误差均最小的准则，而未用现时刻的抽头参量等来对以往各时刻的数据块均作重新估计后的累积平方误差最小的原则(即所谓的最小平方(LS )准则)。

为了克服收敛速度慢，信号非平稳适应性差的缺点，根据上述内容，可采用新的准则，即在每时刻对所有已输入信号而言重估的平方误差和最小的准则(即LS 准则)。

从物理概念上可见，这是个在现有的约束条件下利用了最多可利用信息的准则，即在一定意义上最有效，信号非平稳的适应性能也应最好的准则。

这样建立起来的迭代方法就是递归最小二乘(RLS ：Recursive Least Square )算法，又称为广义Kalman 自适应算法。

用矩阵的形式表示RLS 算法非常方便，因此我们首先定义一些向量和矩阵。

假定在时刻t ，均衡器的输入信号为t r ，线性均衡器对于信息符号的估计可以表示为∑-=--=KK j j t j r t c t I )1()(ˆ 式(3-1)让)1(-t c j 的下标j 从0=j 到1-=N j ，同时定义K t v t y +=)(，则)(ˆt I变为 ∑-=--=10)()1()(ˆN j jj t y t c t I )()1(t Y t C N N-'= 式(3-2) 其中)1(-t C N 和)(t Y N 分别为均衡器系数)1(-t c j ，1,,1,0-=N j 和输入信号)(j t y -，1,,1,0-=N j 的列向量。

类似的，在DFE 均衡器结构中，均衡器系数)(t c j ，1,,1,0-=N j 的前11+K 个系数为前向滤波器系数，剩下的112--=K N K 为反馈滤波器系数。