LMS 算法自适应均衡器实验08S005073 房永奎一、实验目的1、掌握LMS 算法的计算过程，加深对LMS 算法的理解。
2、研究用LMS 算法自适应均衡引起失真的线性色散信道问题。
3、研究特征值扩散度()R χ和步长参数μ对学习曲线的影响。
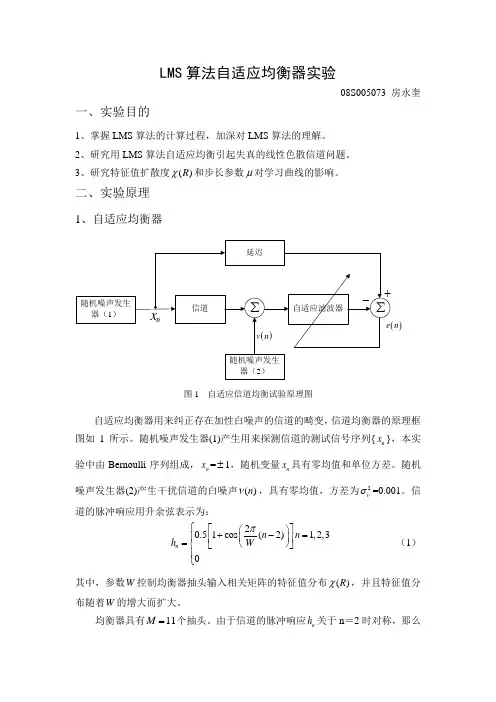
二、实验原理1、自适应均衡器)n图1 自适应信道均衡试验原理图自适应均衡器用来纠正存在加性白噪声的信道的畸变，信道均衡器的原理框图如1所示。
随机噪声发生器(1)产生用来探测信道的测试信号序列{n x }，本实验中由Bernoulli 序列组成，n x =±1，随机变量n x 具有零均值和单位方差。
随机噪声发生器(2)产生干扰信道的白噪声()n ν，具有零均值，方差为2νσ=0.001。
信道的脉冲响应用升余弦表示为：20.51cos (2)1,2,30n n n h W π⎧⎡⎤⎛⎫+-=⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪⎩（1） 其中，参数W 控制均衡器抽头输入相关矩阵的特征值分布()R χ，并且特征值分布随着W 的增大而扩大。
均衡器具有11M =个抽头。
由于信道的脉冲响应n h 关于n ＝2时对称，那么均衡器的最优抽头权值on ω在5n =时对称。
因此，信道的输入n x 被延时了257∆=+=个样值，以便提供均衡器的期望响应。
通过选择匹配横向均衡器中点的合适延时∆，LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。
2、均衡器输入相关矩阵在时刻n ，均衡器第1个抽头的输入为()()()31k k u n h x n k v n ==-+∑ （2）其中所有参数均为实数。
因此，均衡器输入的11个抽头(),(1),,(10)u n u n u n --的自相关矩阵R 为一个对称的1111⨯矩阵。
此外，因为脉冲响应n h 仅在1,2,3n =时为非零，且噪声过程()v n 是零均值、方差为2v σ的白噪声，因此相关矩阵R 是主对角线的，有以下特殊结构所示：()()()()()()()()()()()()()()()012001012021010021000000r r r r r r r r r r r r r r r ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦R （3） 其中()22221230v r h h h σ=+++ （4）()12231r h h h h =+ （5）()132r h h = （6）其中方差20.001v σ=。
