中心复合设计

响应面实验次数计算摘要：响应面实验次数计算1.响应面实验简介2.实验次数计算方法3.计算实例4.结果分析与讨论正文：响应面实验次数计算响应面实验是一种通过改变实验条件，观察响应变量变化以寻找最优实验条件的方法。

在进行响应面实验时，选择合适的实验次数至关重要，既要保证实验的有效性，又要避免实验资源的浪费。

本文将介绍一种计算响应面实验次数的方法。

实验次数计算方法主要基于中心复合设计（CCD）和Box-Behnken 设计（BBD）。

这两种设计方法都可以用来优化实验条件，提高实验的有效性。

在实际应用中，可以根据实验的具体需求选择合适的设计方法。

1.响应面实验简介响应面实验是一种实验设计方法，通过改变实验条件（输入变量），观察响应变量（输出变量）的变化，以寻找最优实验条件。

响应面实验通常采用多因素实验设计，涉及多个输入变量和输出变量。

实验过程中，通过对输入变量进行组合，得到不同的实验条件，从而获得响应变量的变化情况。

2.实验次数计算方法实验次数的计算方法主要基于中心复合设计（CCD）和Box-Behnken 设计（BBD）。

这两种设计方法都可以用来优化实验条件，提高实验的有效性。

（1）中心复合设计（CCD）中心复合设计是一种具有代表性的实验设计方法，适用于寻找影响响应变量的主导因素。

CCD 通过对输入变量进行组合，得到一系列实验条件，同时保证每个输入变量的变化范围在一定范围内。

实验次数的计算公式为：= (p + 1)(p + 2)/2其中，n 为实验次数，p 为输入变量的个数。

（2）Box-Behnken 设计（BBD）Box-Behnken 设计是一种更灵活的实验设计方法，适用于寻找多个输入变量对响应变量的交互影响。

BBD 通过对输入变量进行组合，得到一系列实验条件，同时保证每个输入变量的变化范围在一定范围内。

实验次数的计算公式为：= (p + 1)(p + 2)(p + 3)/6其中，n 为实验次数，p 为输入变量的个数。

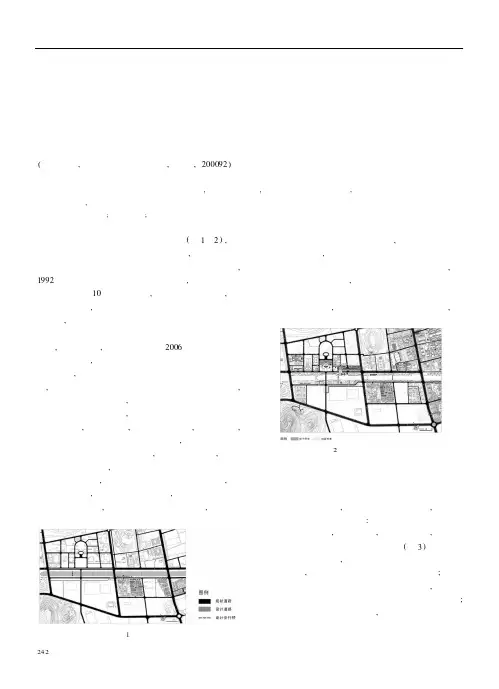
以水为核心的生态、行为复合中心———铜山县城中心城市设计卢济威　张凡　张力(同济大学,建筑与城市规划学院,上海,200092)【摘要】城市设计充分发挥自然生态资源的作用,以水为和核心,运用自然生态网络建设,功能空间交混组织和立体广场群构筑等方法,创造活力盎然、环境宜人和特色鲜明的县城中心。

【关键词】生态资源;县城中心;城市设计图　区位图 铜山县位于江苏省徐州市的南侧(图1、2),是徐州南部的综合性城区和特色的副中心,也是徐州优质生态居住发展区。

铜山县城原与徐州市区交混,1992年批准决定建设独立的县城中心,并移至现在的位置。

经过10多年的建设,已形成基本格局,路网框架已建成,县府行政办事机构结合广场已形成市政中心,沿县城东侧的北京路和行政中心的周边已建成大量居住区和相关公共建筑。

然而总体看县城建设松散,缺乏中心,没有凝聚力。

2006年县政府完成城区总体规划,规定沿楚河为县城中心发展区。

作为中小城市,中心区首先应该是商业、金融、服务中心,同时也应该是文化、娱乐中心和行政办公中心,这些公共设施大量聚集,有利于城市活力的形成。

一方面虽然经过多年建设,县城中心区域现状还是单一的行政中心,既无商业,又缺服务设施,布局分散,没有人气。

建县城之初急于形成气氛,由政府投资建行政办公机构有其充分的理由,但发展到今天,城市进入新的发展时期,需要结合总体规划制定新的建设计划。

另一方面,楚河作为城市极佳的环境资源,却没有充分利用,按常规的绿带建设,并有城市干道将城区与水体隔离,滨水区驻留者了了无几,十分冷清。

水是城市生态的重要组成要素,在我国长江以北地区更显得重要,如何将水环境作为生态资源充分发挥作用是本课题的重要目标。

楚河作为生态资源,如果能促进形成景观环境,而且又能形成城市的活力场所是最好的选择。

将水环境努力构建成自然生态与行为活动的复合中心,是城市资源运用的理想目标,也是城市设计的追求。

图2　现状与设计范围一、城市设计目标根据上面的分析,以及总体规划的要求,确定铜山县城中心的城市设计目标:建设环境宜人,活力盎然,特色鲜明的,以水为核心的生态、行为复合的县城中心。

1.RSM的四大类型：CCC中心复合序贯设计，CCI中心复合有界设计，CCF中心复合表面设计，BB Box-Behnken设计。

既具有序贯性又具有旋转性的：CCC，只有旋转性的:CCI和BB，只有序xx性的CCF。

具有序贯性的CCC和CCF都含有8个角点（以三因子为例），不具有序贯性的CCI和BB都没经过8个角点（以三因子为例）。

而8个角点是在RSM之前的全因子设计前已经有响应数据的，CCC和CCF可以利用全因子的实验数据，不需要再对角点做实验收集数据。

因此，我对序贯性的理解是能否利用前面全因子角点Y的实验数据，也即前面全因子设计的结果是否可用。

2.具有旋转性的CCC和CCI和BB，CCC可以用通过角点的外接圆球覆盖星点，CCI可以通过角点的内接圆球覆盖星点。

BB也可以用近似的圆球覆盖所有的点。

所以，我对旋转性的理解是能否用一个圆球的球面和球心覆盖所有的实验点。

根据上面的描述，如果全因子是个立方体，则CCC是立方体再加个外接球，CCI是立方体再加个内接球，CCF是立方体再加立方体六个面的中点，BB是立方体12条边的中心点。

它们之间的关系也就清晰了。

其实旋转性是指实验因子水平设计结构上的特性。

在计算信息函数时，有旋转性的设计，要比没有旋转性的设计简化很多。

打个简单比方：在一个正方形的边上，任何点的定位都需要两个参数（X,Y)，然而在一个圆上，所有点的定位只需要一个参数（角度）。

CCF设计就是因为所有设计的角点和星点都不在一个圆或者类圆上，因此缺乏旋转性。

但是CCF的角点是和之前一阶设计的实验水平组合是完全相同的，所以可以沿用，因而有旋转性。

而CCI和CCC以及BB设计是旋转设计，弹CCI和BB设计是没有序贯性的。

“序xx试验”通俗点就是“xx试验”。

用全因子2水平+N中心点试验做试探性试验，看看试验是否真的覆盖到了最高峰或最低峰（弯曲项失拟）；若没有，则改变因子水平继续做下去，如此，直到有为止；若真有，则接着做RSM中除去上面试验部分，新做的部分+上面做的部分=RSM试验这样就把前面试验充分利用起来，合二为一，有机连接；这样就大大降低了试验次数和成本。