下载文档原格式
探索DOE优化的奥秘（DOE系列之四）经过筛选设计的精简或完全析因设计的描述，很多人会满足已经取得的成绩，但也有一些精益求精的人会提出这样的问题：现有的最佳因子水平组合一定是所有因子设置中最理想的选择吗？如果不是，又应当如何找出最优化的因子设置？确实，析因类的DOE更侧重于分析哪些因子是重要的，到底有多重要以及它们之间是否会相互影响，却没有刻意去从整体中寻觅最佳的因子设置。
为了解决这个问题，需要引入DOE中另一种设计类型——响应曲面方法(Response Surface Methodology, 即RSM)，这也是我们本期DOE系列介绍的主题。
在实际工作中，常常需要研究响应变量Y究竟如何依赖于自变量X，进而能够找到自变量的设置使得响应变量获得最佳值。
当自变量的个数较少（通常不超过3个）时，则响应曲面方法是最值得推荐的方法，它尤其适合于响应变量望大（即越大越好）和望小（即越小越好）的情形。
通常来说，DOE的核心技术可分为实验计划和数据分析两大类，响应曲面方法也不例外。
在数据分析方面，它和以前介绍的方法没有什么本质的不同，但在实验计划方面，则有显著的改进。
响应曲面方法的实验计划主要有中心复合设计和Box-Behnken设计两种形式，具体用图形说明如下。
图-1 三因子中心复合设计布点示意图图-1是以三维空间立方体的形式展示了一个典型的三因子的中心复合设计的实验计划示意图，在以下的叙述中给出的坐标都已将各因子代码化。
整个实验由下面三部分实验点构成。
1.立方体点(Cube Point)，用蓝色点表示。
各点坐标皆为1或-1，这是与完全析因设计相同的部分。
2.中心点(Center Point)，用绿色点表示。
各点的三维坐标皆为0。
3.轴点(Axial Point)，用黄色点表示。
除了一维自变量坐标为±α（旋转性指数）外，其余维度的自变量坐标皆为0。
在三因子情况下，共有6个轴点。
当取k4=2α(k为因子个数)时，该类中心复合设计兼具旋转性和序贯性的优点，是最典型的α值设定情形。
中心复合设计原理
中心复合设计原理（Composite Design Pattern）是一种结构型
设计模式，它允许客户端统一处理单个对象和对象组合。
该模式以一种递归的方式组织对象，使得客户端可以像处理单个对象一样处理对象组合。
这个模式常被用于树状结构的场景。
中心复合设计原理包含以下几个关键角色：
1. 组件（Component）：定义对象的一些基本操作，它可以是
接口或抽象类。
这个角色通常包含了对子组件（组合的对象）的操作方法，比如添加、删除、获取子组件等。
2. 叶子组件（Leaf Component）：是组合中的具体单个对象，
不能再包含其他对象，实现组件接口。
3. 容器组件（Composite Component）：是组合中的具体对象
容器，能够包含其他对象，实现组件接口。
容器组件通常会调用其子组件的操作方法，并进行一些额外的操作。
使用中心复合设计原理的主要优点包括：
1. 客户端统一处理单个对象和对象组合，简化了客户端的代码。
2. 可以递归地组织对象，提供管理复杂对象结构的能力。
3. 可以方便地新增新的组件类型，符合开闭原则。
然而，中心复合设计原理也有一些缺点：
1. 在处理具体组合和单个对象时，需要额外的类型判断，可能会导致代码的复杂性增加。
2. 可能会降低系统的性能，因为递归遍历对象组合可能需要较长的时间。
中心复合序贯设计中心复合序贯设计是一种实验设计方法，它可以同时考虑多个因素对实验结果的影响，从而得出更加准确的结论。
本文将从以下几个方面进行详细介绍：一、中心复合序贯设计概述中心复合序贯设计是一种全面考虑因素交互作用的实验设计方法，它能够通过少量试验获得大量信息，提高试验效率和精度。
该方法通过将各因素水平在正交表上排列组合，并设置中心点，使各因素之间的交互作用达到最小，从而避免了传统单因素试验所存在的问题。
二、中心复合序贯设计步骤1. 确定试验因素及其水平：首先需要确定试验所涉及的因素及其水平，以便进行正交表的构建。
一般而言，应选择与研究对象相关联的关键性能指标作为试验响应变量，并确定影响该变量的主要因素。
2. 构建正交表：根据所选定的试验因素及其水平数目构建正交表，在其中设置中心点，并按照正交表进行试验。
3. 进行试验：按照正交表进行试验，并记录各组实验数据。
4. 进行统计分析：根据所得到的实验数据进行统计分析，包括方差分析、回归分析等。
5. 优化设计参数：通过对实验结果的分析，确定最佳组合，并进行优化设计参数。
三、中心复合序贯设计的优点1. 节省试验成本：中心复合序贯设计可以通过少量试验获得大量信息，从而节省试验成本。
2. 提高试验效率和精度：中心复合序贯设计能够全面考虑因素交互作用，从而提高试验效率和精度。
3. 可以同时考虑多个因素对实验结果的影响：传统单因素试验只能考虑一个因素对实验结果的影响，而中心复合序贯设计可以同时考虑多个因素对实验结果的影响。
4. 适用性广泛：中心复合序贯设计适用于各种领域的研究，如材料科学、生物医学、环境科学等。
四、中心复合序贯设计应用案例以某食品企业为例，该企业需要研发一种新型饮料，并确定其最佳配方。
该饮料需要满足以下要求：口感好、色泽艳丽、价格适中。
为了确定最佳配方，该企业采用中心复合序贯设计方法进行试验，试验因素包括三种原料的比例、加热温度、搅拌时间等因素。
三水平四因子的中心复合设计中心复合设计（Central Composite Design，CCD）是一种实验设计方法，通常用于多因素、多水平的实验设计。
这种方法可以帮助研究者探索并理解多个变量之间的相互作用，以便找出最优化的条件或找出最佳的实验设计配置。
中心复合设计的具体步骤包括：1．确定因素和水平：确定要研究的因素和它们的水平。
通常，每个因素都有两个或多个水平，这些水平可以是离散的或连续的。
2．确定实验设计点：在因素空间中确定实验设计点。
中心复合设计通常包括中心点、轴点和星点。
中心点是所有因素都处于零水平的点，轴点是因素水平达到最极端的点，星点则是在因素空间中随机选取的点。
3．实施实验：在确定的实验设计点上进行实验，并收集数据。
4．数据分析和模型拟合：对收集到的数据进行统计分析，通常使用回归分析方法来拟合一个数学模型。
这个模型可以帮助理解因素之间的相互作用，以及如何优化实验条件。
5．优化条件确定：根据数学模型的结果，确定最优化的实验条件。
这通常是通过求解数学模型来得到的。
6．验证实验：在最优化的条件下进行验证实验，以确认实验结果的可靠性和可重复性。
中心复合设计的主要特点：1．中心点重复多次，可以更准确地估计随机误差和模型中的纯误差项。
2．设计中含有轴向点（即远离中心点的试验条件），以充分估计二次项和其他高阶项效应。
3．通过较少的实验次数就能获取较多的信息，从而有效地降低实验成本，提高效率。
三水平四因子的中心复合设计是指在三个水平上对四个因素进行中心复合设计。
具体的实验设计点和数据收集、分析和模型拟合等步骤与上述过程类似。
需要注意的是，由于因素数量和水平的增加，实验设计和数据分析的复杂性也会相应增加。
因此，在进行三水平四因子的中心复合设计时，需要更加谨慎地选择实验设计和分析方法，以确保实验结果的准确性和可靠性。
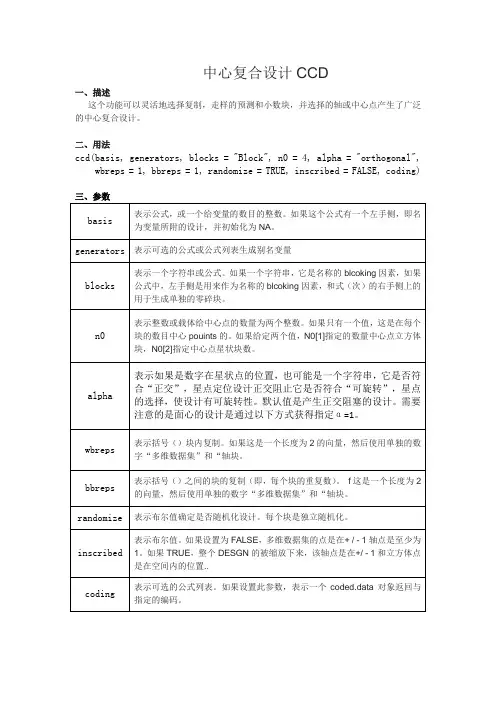
中心复合设计CCD一、描述这个功能可以灵活地选择复制，走样的预测和小数块，并选择的轴或中心点产生了广泛的中心复合设计。
二、用法ccd(basis, generators, blocks = "Block", n0 = 4, alpha = "orthogonal", wbreps = 1, bbreps = 1, randomize = TRUE, inscribed = FALSE, coding)三、参数四、详细信息中央复合设计的CCD响应面勘探中使用的流行的设计。
他们被堵塞的设计组成的至少一种的多维数据集的块（两水平因子或部分因子，附加中心点），和至少一个星状块（点沿每个轴的位置-α+α-），加上中心点。
一切都被假定为规模的编码的多维数据集的设计部分，其中为每个变量的值-1和1，中心点0。
使用的编码参数，如果需要的话，编码可以提供。
基础参数确定一个基本的设计，用来创建立方体块。
例如，basis = ~A+B+C会生成一个基本的8次试验的设计。
如果你需要额外的变量，可使用generators，例如，generators = c(D~-A*B, E~B*C)加在上面定义关系会产生一个5因素设计I = ABD = BCE = ACDE 。
如果你想立方体点分为零碎块，给块参数公式。
例如，basis =A+B+C+D+Egenerators =F~-A*C*D, 和blocks =Day ~c(A*B*C,C*D*E)。
阻挡变量将被命名为“Day”，将其分为4块8和32运行的基本设计（半部分6因素）运行每一个的基础上，结合标志的A * B * C 和C * D * E 。
请注意，这一天将混淆与发电机组，及其相互作用，以及所有这些别名：Day = ABC = CDE = ABDE = -BDF = -ADCF = -BCEF = -AEF。
对于每个模块，我们将添加N0（N0 [1 ]）的中心点。
