关于量子粒子群算法(QPSO)
- 格式:pdf
- 大小:635.23 KB
- 文档页数:3
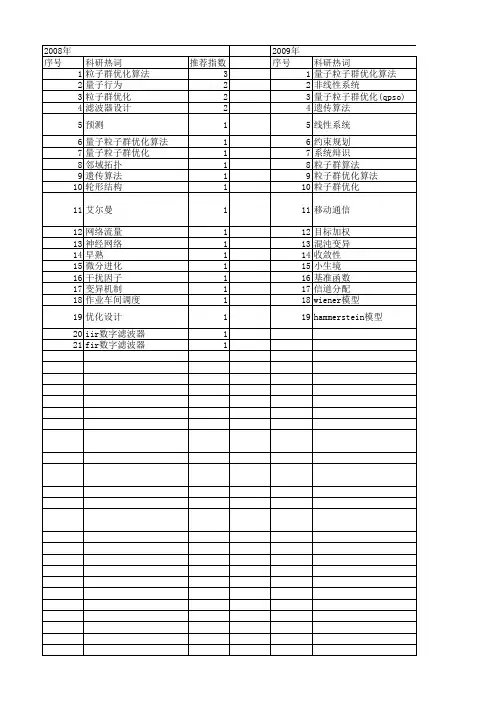

基于QPSO 算法的软件测试数据自动生成李文瑞,张伟,任洪丽摘要:针对目前进化算法生成测试数据方法存在算法复杂、参数设置不易、易陷入局部最优解等缺陷,提出了一种应用于软件测试中的基于量子粒子群算法(QPSO)的测试数据自动生成算法。
该算法是在PSO 算法基础上引入量子理论的思想。
解决了PSO 算法搜索空间有限,容易陷入局部最优解的问题。
通过具体实验证明,该方法是有效可行的,其效率也明显高于GA 算法和PSO 算法。
关键字:软件测试;测试数据生成;粒子群算法;量子粒子群算法0 引言软件测试是软件开发过程中必须完成的重要活动之一,而测试数据的自动生成是软件测试的最关键的问题,可以有效的提高软件测试的效率。
软件测试数据自动生成通常包括功能测试数据自动生成和结构测试数据自动生成,目前通过进化算法生成测试数据方面的研究取得的很大的进展。
文献[1]将遗传算法(GA )应用于面向对象软件的单元测试中,文献[2]提出“分支函数叠加法”来构造适应值函数。
文献[3]对遗传算法在软件测试用例生成的性能进行研究,并提出了两种提高遗传算法生成测试用例效率的方法。
文献[4]将把量子理论应用于PSO 算法中从而提出一种改进的粒子群优化算法。
文献[7]在传统的遗传算法中注入免疫算子,提出了基于免疫遗传算法生成软件测试数据的方法。
文献[8]提出一种基于PSO 算法的软件测试数据生成方法。
但是遗传算法及其改进算法都存在算法复杂、参数设置不易等问题,PSO 算法具有搜索空间有限、容易陷入局部最优解的缺陷。
本文提出一种基于QPSO 的软件测试数据生成方法,并通过实验验证,其效率明显优于遗传算法和粒子群算法,解决了PSO 算法容易陷入局部最优解的缺陷。
1 基本概念1.1 粒子群算法设X i = ( x i1 , x i2 ,…, x in ) 为粒子i 的当前位置;V i = ( v i1 ,v i2 ,…, v in ) 为粒子i 的当前飞行速度;P i = ( p i1 , p i2 , …, p in ) 为粒子i 所经历过的具有最好适应值的位置。


• 160•由于可再生能源深受环境、气候等外部因素影响,作为光伏转换的重要组成部分,当光伏电池发生局部遮挡时,就会伴随出现其特性曲线的多峰值现象。
对于该类情况,传统的电导增量法(incremental conductance,IC )、扰动与观察算法(perturb and observe,P&O )容易误追踪到局部最大功率点(local peak,LP ),导致效率降低。
所以,为了能够准确追踪到全局最大功率点(global peak,GP ),从而保证转换效率,本文提出一种基于量子粒子群算法的最大功率点跟踪技术(maximum power point tracking technique,MPPT )。
通过搭建Matlab 仿真,其结果表明该算法不仅能跟踪到GP ,而且能有效地减小稳态振荡。
在太阳能阵列中,如果出现至少一个光伏电池被遮挡的情况,即属于遮阴现象,若光伏阵列对此没有一些有效的应对保护措施,就会导致光伏系统整体功率的下降,并且受遮挡电池所在的光伏组件会成为负载而消耗功率。
当因此消耗的功率过多时,会造成该组件局部温度过高,甚至导致组件毁坏。
为了尽可能地避免上述问题,可通过给太阳能阵列外接旁路二极管的方法进行解决。
旁路二极管的工作逻辑设计如下:当太阳能阵列的电流未超过被遮挡电池的短路电流I sc 时,受遮挡电池所在支路的旁路二极管不导通;否则,旁路二极管导通,使得电流不从受遮挡的组件上流过,从而降低由此引起的功率消耗。
上述外接旁路二极管,在光照强度均匀照射下不起作用,但是,在受到不均匀光照强度照射时,由于旁路二极管的导通,便会造成太阳能阵列的特性曲线出现多峰值现象。
由此可知,当特性曲线出现多峰值时,传统MPPT 方法不再奏效,且容易陷入局部最大功率点LP 。
针对该问题,本文提出了一种基于量子粒子群算法的MPPT 技术,利用粒子群的全局搜索能力,达到精准追踪全局最大功率点GP 的目的。

基于Qpso算法的应急资源调度应用研究摘要:以连续性消耗应急过程为背景,运用量子行为粒子群算法求解多目标的应急资源调度数学模型。
考虑施救成本费用和因施救不及时造成损失的构造模型的目标函数。
针对该模型的特点,设计量子粒子群算法求解方法和步骤,用数值算例验证了所建立模型的合理性及量子粒子群算法的可行性和有效性。
abstract: a multi-objective emergency-resource scheduling model is established in the continuous consumption emergency system. considering rescue costs and the losses caused by not be rescued in time,the objective function of the model is designed with these two sides. according to the characteristic of the model, the solving procedure and its steps are based on quantum-behaved particle swarm algorithm.a data example verifies the rationality of the model, and the feasibility and the validity of using the quantum-behaved particle swarm optimization.关键词:应急资源;连续消耗;量子行为粒子群优化算法;整数规化key words: emergency resources;continuous consumption;quantum-behaved particle swarm optimization;integer programming中图分类号:tp301.6文献标识码:a 文章编号:1006-4311(2012)34-0205-020 引言目前,我国处于经济高速发展时期的同时,各种突发公共事件也接连不断的发生。

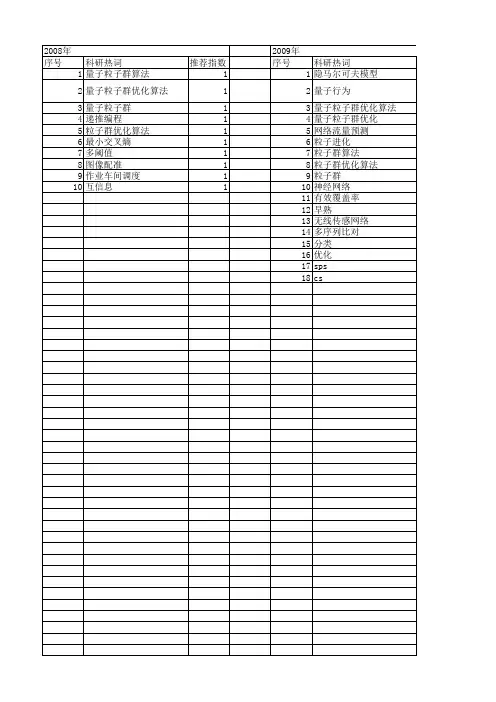


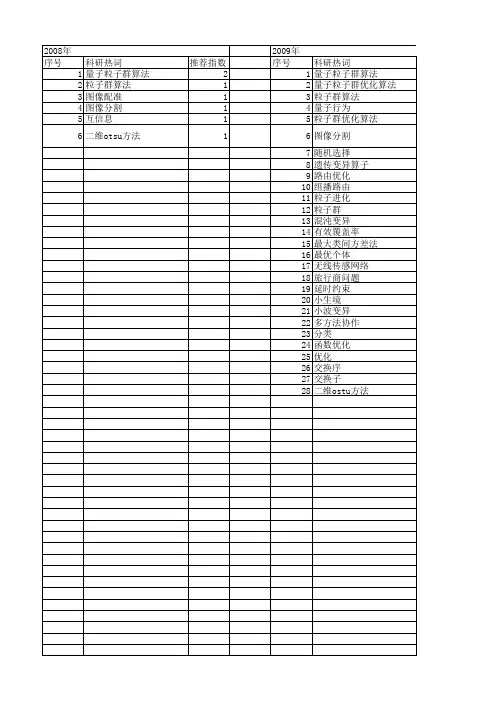

基于MATLAB的量子粒子群优化算法及其应用
余健;郭平
【期刊名称】《计算机与数字工程》
【年(卷),期】2007(35)12
【摘要】量子粒子群优化(QPSO)算法是在经典的粒子群优化(PSO)算法的基础上所提出的一种具有量子行为的粒子群优化算法,具有高效的全局搜索能力.通过求解J.D.Schaffer提出的多峰函数优化问题的实验分析表明,方法具有良好的收敛性和稳定性.
【总页数】2页(P38-39)
【作者】余健;郭平
【作者单位】韩山师范学院数信学院,潮州,521041;北京师范大学信息科学学院,北京,100875
【正文语种】中文
【中图分类】TP301.6
【相关文献】
1.基于CORBA的Matlab随机模型在计算机应用系统中的应用 [J], 权小红
2.一种基于空间混沌序列的量子粒子群优化算法及其应用 [J], 靳雁霞;师志斌
3.应用型本科线性代数教学模式的探索——基于MATLAB在解方程组中应用实践的分析 [J], 孙健;王翠芳
4.应用型本科线性代数教学模式的探索——基于MATLAB在解方程组中应用实践的分析 [J], 孙健;王翠芳;
5.基于MATLAB和ABAQUS的参数智能反分析程序在隧道工程中的应用 [J], 李宁;李昕珍;江昊鸿;张茂建;潘行
因版权原因,仅展示原文概要,查看原文内容请购买。
量子粒子群优化算法在结构参数识别中的应用
王兰彬
【期刊名称】《防灾减灾工程学报》
【年(卷),期】2013()1
【摘要】系统识别问题可以转化成一高维多模优化问题。
针对基本粒子群优化在分析此类问题时容易出现早熟收敛从而导致局部优化和较大误差的缺陷,提出将量子粒子群优化算法(QPSO)应用于结构参数识别。
QPSO具有参数少、编程简单、易实现、收敛速度快、可以避免早熟收敛、能够迅速在全局找到最优解的特点。
本文在测量数据不完备且含噪声污染,参数质量、刚度和阻尼等信息缺乏的情况下,通过数值模拟以及在真实结构参数识别中的应用,验证了QPSO的有效性。
【总页数】6页(P91-96)
【作者】王兰彬
【作者单位】同济大学结构工程与防灾研究所
【正文语种】中文
【中图分类】TU352.1
【相关文献】
1.粒子群优化算法在结构参数识别中的应用
2.量子粒子群算法在结构模态参数识别中的应用
3.量子粒子群优化算法在各向异性含水层参数中的应用
4.多粒子群优化算法和RBF神经网络在缺陷故障参数红外智能识别中的应用
5.多粒子群优化算法和RBF神经网络在缺陷故障参数红外智能识别中的应用
因版权原因,仅展示原文概要,查看原文内容请购买。
量子粒子群优化算法在训练支持向量机中的应用
山艳;须文波;孙俊
【期刊名称】《计算机应用》
【年(卷),期】2006(26)11
【摘要】训练支持向量机的本质问题就是求解二次规划问题,但对大规模的训练样本来说,求解二次规划问题困难很大.遗传算法和粒子群算法等智能搜索技术可以在较少的时间开销内给出问题的近似解.量子粒子群优化(QPSO)算法是在经典的微粒群算法的基础上所提出的一种有较高收敛性和稳定性的进化算法.将操作简单而收敛快速的QPSO算法运用于训练支持向量机,优化求解二次规划问题,为解决大规模的二次规划问题开辟了一条新的途径.
【总页数】4页(P2645-2647,2677)
【作者】山艳;须文波;孙俊
【作者单位】江南大学,信息工程学院,江苏,无锡,214122;江南大学,信息工程学院,江苏,无锡,214122;江南大学,信息工程学院,江苏,无锡,214122
【正文语种】中文
【中图分类】TP181
【相关文献】
1.支持向量机在弹药训练消耗量预测中的应用 [J], 宋彬;龚传信;管维荣
2.改进粒子群算法在支持向量机训练中的应用 [J], 田鹏;潘丰
3.改进量子粒子群优化算法在分子对接中的应用 [J], 傅毅;赵吉
4.改进量子粒子群优化算法在分子对接中的应用 [J], 傅毅;赵吉;;;;
5.混合量子粒子群优化算法在高职院校排课管理系统中的应用 [J], 高建兴
因版权原因,仅展示原文概要,查看原文内容请购买。
关于量子粒子群算法的杂七杂八
1 关于PSO
说到GPSO,必须要说到它的源头,也就是PSO,也就是粒子群算法
按照北京航空航天大学的王小川老师说法,粒子群优化算法(Particle swarm optimization,PSO)是模拟鸟群捕食行为的优化算法。
不同于遗传算法(Genetic Alogrithm,GA),粒子群算法是有记忆的,之前迭代过程中的最优位置和最优方向都会保留下来并作用于粒子群的更新。
这个算法的应用太广了,如果学习了一段时间的机器学习,即将迈入深度学习的阶段,一定要迈过去的两个坎,一个是RBM,就是受限玻尔兹曼机,另一个就是PSO
1.1相关的名词解释
粒子群长度:粒子群长度等于每一个参数取值范围的大小。
粒子群维度:粒子群维度等于待寻优参数的数量。
这个根据项目的具体要求可以十分容易的敲定
粒子群位置:粒子群位置包含参数取值的具体数值。
粒子群方向:粒子群方向表示参数取值的变化方向。
个人感觉这里也可以理解成想原本的粒子(或者是cluster中的拥有实际含义的矩阵)的方向向量进行进一步的分解,从某种意义上说,其实它加大了分解出来的向量之间的联系,算是在某种程度上对于数据的维度进行了一定的扩充。
适应度函数:表征粒子对应的模型评价指标。
关于适应度函数的取值其实不止一个算法或者是模型中提到了关于适应度函数的具体含义与在具有特定条件与背景之下可能有效的适应度函数的取法,经典的如北京航空航天大学的王小川老师在他的著作中认为可以将适应度函数的取值设定为cluster中的单个样本的值对应的总的cluster的mean值的均方差的倒数,当然这个说法并不唯一,而且是在不同的条件下取值并不完全相同。
《43个案例分析》中单只要是涉及到函数的拟合的,适应度函数的取值都为待拟合的函数的取值的倒数。
目前尚无较为肯定的经验公式或者是对应的参照物图表可以归纳所有情况。
pbest:(局部最优)pbest的长度等于粒子群长度,表示每一个参数取值的变化过程中,到目前为止最优适应度函数值对应的取值。
gbest:(全局最优)gbest的长度为1,表示到目前为止所有适应度函数值中最优的那个对应的参数取值。
1.2关于粒子的更新
在对于具有实际含义的矢量进行了分解之后,使用不同的矢量表示出原本的矢量,写成坐标
的形式
设定出取随机数在某种意义上也是为了代际过多的时候规避可能会出现的局部极小值问题,相当于使用了别的可能造成系统重新进行选路操作的算法进行优化,当然了,这种算法必然存在一定的随机性。
这种情况下粒子的更新变量为
2 由此衍生而来的GPSO
2.1前言
PSO算法的缺点:
1、需要设定的参数(惯性因子局部学习因子和全局学习因子)太多,不利于找到待优化模型的最优参数。
但是我感觉这个其实不算很明显的确定,只是对于新手而言不那么友好
2、粒子位置变化缺少随机性,容易陷入局部最优的陷阱。
这个确实是制约PSO的一个地方,这个时候可以介入第三方算法对于这种陷入局部极小值的情况进行路线的修正。
有的修正是局部的修正,必要的时候也可以进行全局的修正,不过进行全局的修正的时候需要慎重。
2.2改进的地方
量子粒子群优化(Quantum Particle Swarm Optimization,QPSO)算法取消了粒子的移动方向属性,粒子位置的更新跟该粒子之前的运动没有任何关系,这样就增加了粒子位置的随机性比较明显的史诗级更新在于其引入了一个新的量
mbest:表示pbest的平均值,即平均的粒子历史最好位置。
其实强调粒子的平均位置这个更加属于贝叶斯风格的分析问题的方式,与频率方式分析机器学习问题的方式差别更大
2.3具体计算步骤2.
3.1首先计算mbest
2.3.2进行位置的更新。