当前位置：文档之家 › 空间插值方法对比整理版 (1)

空间插值方法对比整理版 (1)

  • 格式：ppt
  • 大小：1.59 MB
  • 文档页数：56

下载文档原格式

  / 56

合集下载

空间插值方法对比整理版

空间插值方法对比整理版

• 由于建立在统计学的基础上，因此不仅可 以产生预测曲面，而且可以产生误差和不 确定性曲面，用来评估预测结果的好坏
• 多种 kriging 方法
a
9
3、精确插值和近似插值
• 精确插值：产生通过所有观测点的曲面。
• 在精确插值中，插值点落在观测点上，内插值等 于估计值。
• 近似插值：插值产生的曲面不通过所有观测 点。
a
11
插值方法选择的原则
① 精确性：
② 参数的敏感性：许多的插值方法都涉及到一个或多个参数， 如距离反比法中距离的阶数等。有些方法对参数的选择相当 敏感，而有些方法对变量值敏感。后者对不同的数据集会有 截然不同的插值结果。希望找到对参数的波动相对稳定，其 值不过多地依赖变量值的插值方法。
③ 耗时：一般情况下，计算时间不是很重要，除非特别费时。
空间插值 Spatial Interpolation
• 空间插值的概念 • 空间插值的类型 • 空间插值的方法
a
1
空间插值概念
空间插值——空间插值常用于将离散点的测量数据转换为连 续的数据曲面，以便与其它空间现象的分布模式进行比较， 它包括了空间内插和外推两种算法。空间内插算法：通过已 知点的数据推求同一区域未知点数据。空间外推算法：通过 已知区域的数据，推求其它区域数据。
• 典型例子是：全局趋势面分析 、Fourier Series （周期序列）
a
4
局部内插法
➢ 局部内插法只使用邻近的数据点来估计未知点的值，步骤如 下： • 定义一个邻域或搜索范围； • 搜索落在此邻域范围的数据点； • 选择能表达这有限个点空间变化的数学函数； • 为未知的数据点赋值。
➢ 局部内插方法： • 样条函数插值法 • 距离倒数插值 • Kriging插值（空间自由协方差最佳内插）

空间插值算法汇总

空间插值算法汇总

空间插值算法：1、距离倒数乘方法（Inverse Distance to a Power）距离倒数乘方格网化方法是一个加权平均插值法，可以进行确切的或者圆滑的方式插值。

方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。

对于一个较大的方次，较近的数据点被给定一个较高的权重份额，对于一个较小的方次，权重比较均匀地分配给各数据点。

计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。

当计算一个格网结点时，配给的权重是一个分数，所有权重的总和等于1.0。

当一个观测点与一个格网结点重合时，该观测点被给予一个实际为 1.0 的权重，所有其它观测点被给予一个几乎为0.0 的权重。

换言之，该结点被赋给与观测点一致的值。

这就是一个准确插值。

距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。

用距离倒数格网化时可以指定一个圆滑参数。

大于零的圆滑参数保证，对于一个特定的结点，没有哪个观测点被赋予全部的权值，即使观测点与该结点重合也是如此。

圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。

2、克里金法（Kriging）克里金法是一种在许多领域都很有用的地质统计格网化方法。

克里金法试图那样表示隐含在你的数据中的趋势，例如，高点会是沿一个脊连接，而不是被牛眼形等值线所孤立。

克里金法中包含了几个因子：变化图模型，漂移类型和矿块效应。

3、最小曲率法（Minimum Curvature）最小曲率法广泛用于地球科学。

用最小曲率法生成的插值面类似于一个通过各个数据值的，具有最小弯曲量的长条形薄弹性片。

最小曲率法，试图在尽可能严格地尊重数据的同时，生成尽可能圆滑的曲面。

使用最小曲率法时要涉及到两个参数：最大残差参数和最大循环次数参数来控制最小曲率的收敛标准。

4、多元回归法（Polynomial Regression）多元回归被用来确定你的数据的大规模的趋势和图案。

空间插值方法大致总结

空间插值方法大致总结

前段时间要对气象要素进行插值,翻看了多种方法,做了个PPT报告.对每个方法有简单的介绍极一些总结,不一定都是个人看法,参考了多方书面(sufer,ArcGIS应用教程)以及坛子里,百度上等搜到的资料的看后笔记,有些注了出处有些忘了.截图共享下,也不知有用没用.有错的地方请跟贴指正,谢谢啦!--------------------------------所谓空间数据插值,即通过探寻收集到的样点/样方数据的规律,外推/内插到整个研究区域为面数据的方法.即根据已知区域的数据求算待估区域值, 影响插值精度的主要因素就是插值法的选取空间数据插值方法的基本原理:任何一种空间数据插值法都是基于空间相关性的基础上进行的。

即空间位置上越靠近,则事物或现象就越相似, 空间位置越远,则越相异或者越不相关，体现了事物/现象对空间位置的依赖关系。

（/dky/nb/page/2000-3-3/2000332117262480.htm，南京师范大学地理科学学院地理信息系统专业网络课程教程）➢由于经典统计建模通常要求因变量是纯随机独立变量，而空间插值则要求插值变量具备某种程度的空间自相关性的具随机性和结构性的区域化变量。

即区域内部是随机的，与位置无关的，而在整体的空间分布上又是有一定的规律可循的，这也是不宜用简单的统计分析方法进行插值预估的原因。

从而空间统计学应用而生。

➢无论用哪种插值方法，根据统计学假设可知，样本点越多越好，而样本的分布越均匀越好。

常用的空间数据插值方法之一：趋势面分析⏹趋势面分析（Trend analyst）。

严格来说趋势面分析并不是在一种空间数据插值法。

它是根据采样点的地理坐标X，Y值与样点的属性Z值建立多元回归模型，前提假设是，Z值是独立变量且呈正态分布，其回归误差与位置无关。

⏹根据自行设置的参数可建立线性、二次…或n次多项式回归模型，从而得到不同的拟合平面，可以是平面，亦可以是曲面。

精度以最小二乘法进行验证。

空间插值介绍简洁明了

空间插值介绍简洁明了

一、最近邻法(Nearest Neighbor)
• 最近邻点法又叫泰森多边形方法。它采用一种极端的边界内 插方法—只用最近的单个点进行区域插值（区域赋值）。 • 泰森多边形按数据点位置将区域分割成子区域，每个子区域 包含一个数据点，各子区域到其内数据点的距离小于任何到 其它数据点的距离，并用其内数据点进行赋值。
（2）“实际”验证
将部分已知变量值的样本点作为“训练数据集”，用于插值 计算；另一部分样点 “验证数据集”，该部分站点不参加 插值计算。然后利用“训练数据集” 样点进行内插，插值 结果与“训练数据集”验证样点的观测值对比，比较插值的 效果。
插值方法
1. 最近邻法(Nearest Neighbor) 2. 算术平均值(Arithmetic Mean) 3. 距离反比法(Inverse Distance) 4. 高次曲面插值(Multiquadric) 5. 趋势面插值(Polynomial) 6. 最优插值(Optimal) 7. 样条插值(Spline Surface) 8. 径向基函数插值(Radial Basis Functions) 9. 克里金插值(Kriging) 10. 最小曲率 (Minimum Curvature)
四、高次曲面插值 (Multiquadric)
高次曲面插值由 Hardy 于1971年首先提出，随后应用于不同的 学科。每个样点对插值点的影响都用样点坐标函数构成的圆锥表 示，插值点的变量值是所有圆锥贡献值的总和(Caruso,1998)。 插值数学表达式为：
ve ci d ei
i 1
其中ci 是样本点（xi，yi）的系数，dei是待估点（xe, ye）与样 本点（xi, yi）的距离。
• 反距离权重插值综合了泰森多边形的自然邻近法和多元回归渐变 方法的长处，在插值时为待估点Z值为邻近区域内所有数据点都 的距离加权平均值，当有各向异性时，还要考虑方向权重。 • 权重函数与待估点到样点间的距离的U次幂成反比，即随着距离 增大，权重呈幂函数递减。且对某待估点而言，其所有邻域的样 点数的权重和为1。 • 决定反距离权重插值法结果的参数包括距离的U次幂值的确定， 同时还取决于确定邻近区域的所使用的方法。此外，为消除样点 数据的不均匀分布的影响，还可设置引入一个平滑参数，以保证 没有哪个样点被赋予全部的权重，即使得插值运算时尽可能不只 有一个样点参与运算。 • IDW是一种全局插值法，即全部样点都参与某一待估点的Z值的 估算； • IDW的适用于呈均匀分布且密集程度足以反映局部差异的样点数 据集； • IDW与之前介绍的插值法的不同之处在于，它是一种精确的插值 法，即插值生成的表面中预测的样点值与实测样点值完全相等。

基于ArcGIS的空间插值方法比较

基于ArcGIS的空间插值方法比较

的整体数据特征基本一致，且拉伸领域相比克里金插值更加接 近原始数据分布特征，而克里金插值数据变化幅度较大。下面 将通过使用监测点进行精度模型评价，表 1 为两种插值法检验 数据统计结果。表 2 为插值精度比。
表 1 插值检验数据统计
OBJECTID 1 2 3 4 5 6 7
heigh 60 51 102 96 124 100 58
表 2 两种插值法精度比较
方法
ＲMSE Ｒ-ＲMSE L-ＲMSE ME
SD
AＲ
反距离插值法 14．353 0．1913 0．2012 3．1742 14．5012 1．0124
克里金插值法 20．253 0．2625 0．2603 3．3618 20．0545 1．0113
图 1 数据原始数据与高程点数据 2．2 结果评价及改进思路 图 2 为反距离插值、克里金插值算法拉伸柱状图比较。
图 2 两种插值算法拉伸柱状图统计比较图 （ 左侧为反距离插值，右侧为克里金插值） 从图 2 的拉伸柱状图统计比较图中可以看出，反距离插值
从上表中可以看出，克里金插值法的误差以及平均误差远 大于反距离插值法，这也证明了前文中所说的克里金插值所计 算的结果波动较大，因此，就针对该组高程数据来说使用克里 金插值法的效果更好。
3 结语 使用科学合理的插值方法可以节约大量的时间，提升空间 信息数据获取与预测的效率，现今，各类插值技术以及使用都 较为成熟，相信在不久的将来，插值算法的自动性会更高，多尺 度建模以及多维表达形式更加完备。 参考文献： ［1］周海荣，张亮，俞伟柯，寿祝欢，卢月明． 基于自适应采 样的空间插值 方 法 比 较 研 究［J］． 科 学 技 术 创 新，2018 （ 04） ： 8-11． ［2］肖城龙．基于 ArcGIS 的空间数据插值方法的研究与实 验［J］．城市勘测，2017（ 06） ： 71-73+83．

空间插值方法对比整理版1ppt课件

空间插值方法对比整理版1ppt课件

方次，较近的数据点被给定一个较高的权重份额，对于一个
较小的方次，权重比较均匀地分配给各数据点。计算一个格
网结点时给予一个特定数据点的权值与指定方次的从结点到
观测点的该结点被赋予距离倒数成比例。当计算一个格网结
点时，配给的权重是一个分数，所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时，该观测点被给予一个
一般插值过程
内插方法（模型）的选择； 空间数据的探索性分析，包括对数据的均值、方
差、协方差、独立性和变异函数的估计等； 进行内插； 内插结果评价； 重新选择内插方法，直到合理； 内插生成最后结果。
10
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
（2）“实际”验证 将部分已知变量值的样本点作为“训练数据集”，用于插值 计算；另一部分样点 “验证数据集”，该部分站点不参加 插值计算。然后利用“训练数据集” 样点进行内插，插值 结果与“训练数据集”验证样点的观测值对比，比较插值的 效果。
12
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
17
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
算术平均值法评价
算术平均值的算法比较简单，容易实现。但只考虑算术 平均，根本没有顾及其他的空间因素，这也是其一个致命的 弱点，因而在实际应用中效果不理想。
插值方法选择的原则

(完整word版)空间内插方法比较

一、空间数据的插值用各种方法采集的空间数据往往是按用户自己的要求获取的采样观测值，亦既数据集合是由感兴趣的区 域内的随机点或规则网点上的观测值组成的。

但有时用户却需要获取未观测点上的数据，而已观测点上的数 据的空间分布使我们有可能从已知点的数据推算岀未知点的数据值。

在已观测点的区域内估算未观测点的数据的过程称为内插；在已观测点的区域外估算未观测点的数据的 过程称为外推。

空间数据的内插和外推在 GIS 中使用十分普遍。

一般情况下，空间位置越靠近的点越有可能获得与 实际值相似的数据，而空间位置越远的点则获得与实际值相似的数据的可能性越小。

下面介绍一些常用的内 插方法。

1、边界内插使用边界内插法时，首先要假定任何重要的变化都发生在区域的边界上，边界内的变化则是均匀的、同质的。

边界内插的方法之一是泰森多边形法。

泰森多边形法的基本原理是，未知点的最佳值由最邻近的观测值产生。

如图4-6-1所示。

泰森多边形的生成算法见§ 5.7。

2、趋势面分析趋势面分析是一种多项式回归分析技术。

多项式回归的基本思想是用多项式表示线或面，按最小二乘法原理对数据点进行拟合， 拟合时假定数据点的空间坐标 X 、Y 为独立变量，而表示特征值的Z 坐标为因变 量。

当数据为一维时，可用回归线近似表示为：-其中，Sb 、a i 为多项式的系数。

当n 个采样点方差和为最小时，则认为线性回归方程与被拟合曲线达工（N -乳〕之-min到了最佳配准，如图4-6-2左图所示，即： 一当数据以更为复杂的方式变化时，如图 4-6-2右图所示。

在这种情况下，需要用到二次或高次多项式:在GIS 中，数据往往是二维的，在这种情况下，需要用到二元二次或高次多项式:£ 二 ％ + a x X + a^X（二次曲线）7 1= +O,JV 2 +a 4J¥y4多项式的次数并非越高越好，超过 3次的多元多项式往往会导致奇异解，因此，通常使用二次多项 式。

空间曲线插值

空间曲线插值
空间曲线插值是指通过一系列已知的空间点，推导出两个或多个点之间的中间位置，从而形成一条平滑的曲线。

这种插值方法广泛应用于计算机图形学、计算机辅助设计以及三维动画等领域。

在空间曲线插值中，常用的方法包括线性插值、贝塞尔曲线插值和样条曲线插值。

1. 线性插值：线性插值是最简单的插值方法，它假设两个点之间的曲线段为一条直线。

通过计算两个点之间的距离和方向，可以得到中间点的位置。

线性插值适用于需要简单粗暴的连接两个点的情况，但不能提供更复杂的曲线形状。

2. 贝塞尔曲线插值：贝塞尔曲线插值是通过控制点来定义曲线形状的一种方法。

贝塞尔曲线可以通过调整控制点的位置和权重来改变曲线的形状。

常见的贝塞尔曲线包括二次贝塞尔曲线和三次贝塞尔曲线，它们分别由2个和3个控制点定义。

贝塞尔曲线插值可以提供更加自由和灵活的曲线形状。

3. 样条曲线插值：样条曲线插值是一种基于局部控制的插值方法，它通过一系列的支撑点和控制点来定义曲线。

样条曲线可以保持平滑，并且可以通过调整控制点的位置来改变曲线的形状。

常见的样条曲线包括B样条曲线和NURBS曲线。

样条曲线插值适用于需要精确控制曲线形状的情况，例如在计算机辅助设计中绘制曲线路径。

总之，空间曲线插值是一种通过已知点推导出中间点位置的方法，可以通过线性插值、贝塞尔曲线插值和样条曲线插值等方法实现。

选
择合适的插值方法取决于需要的曲线形状和应用场景。

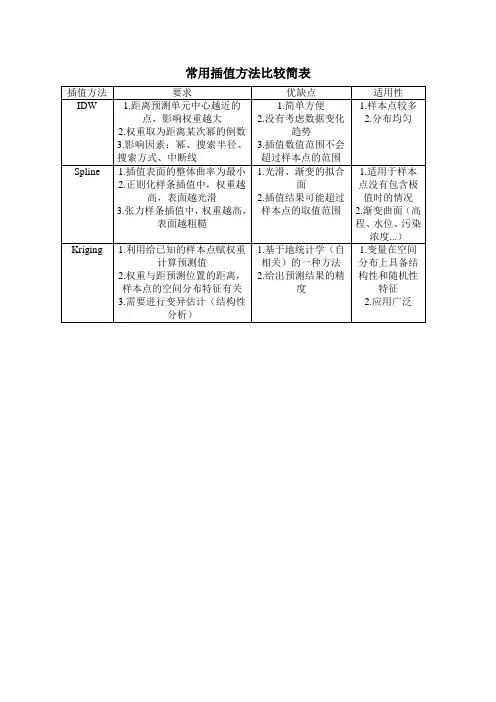
常用插值方法比较简表

常用插值方法比较简表
插值方法要求优缺点适用性
IDW 1.距离预测单元中心越近的
点，影响权重越大
2.权重取为距离某次幂的倒数
3.影响因素：幂、搜索半径、
搜索方式、中断线
1.简单方便
2.没有考虑数据变化
趋势
3.插值数值范围不会
超过样本点的范围
1.样本点较多
2.分布均匀
Spline 1.插值表面的整体曲率为最小
2.正则化样条插值中，权重越
高，表面越光滑
3.张力样条插值中，权重越高，
表面越粗糙1.光滑、渐变的拟合
面
2.插值结果可能超过
样本点的取值范围
1.适用于样本
点没有包含极
值时的情况
2.渐变曲面（高
程、水位、污染
浓度...）
Kriging 1.利用给已知的样本点赋权重
计算预测值
2.权重与距预测位置的距离，
样本点的空间分布特征有关
3.需要进行变异估计（结构性
分析）1.基于地统计学（自
相关）的一种方法
2.给出预测结果的精
度
1.变量在空间
分布上具备结
构性和随机性
特征
2.应用广泛。

空间插值方法汇总

空间插值方法汇总(2010-08-05 21:13:33)在科学计算领域中，空间插值是一类常用的重要算法，很多相关软件都内置该算法，其中GodenSoftware 公司的Surfer软件具有很强的代表性，内置有比较全面的空间插值算法，主要包括：Inverse Distance to a Power（反距离加权插值法）Kriging（克里金插值法）Minimum Curvature（最小曲率）Modified Shepard's Method（改进谢别德法）Natural Neighbor（自然邻点插值法）Nearest Neighbor（最近邻点插值法）Polynomial Regression（多元回归法）Radial Basis Function（径向基函数法）Triangulation with Linear Interpolation（线性插值三角网法）Moving Average（移动平均法）Local Polynomial（局部多项式法）下面简单说明不同算法的特点。

1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法，可以进行确切的或者圆滑的方式插值。

方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。

对于一个较大的方次，较近的数据点被给定一个较高的权重份额，对于一个较小的方次，权重比较均匀地分配给各数据点。

计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。

当计算一个格网结点时，配给的权重是一个分数，所有权重的总和等于1.0。

当一个观测点与一个格网结点重合时，该观测点被给予一个实际为1.0 的权重，所有其它观测点被给予一个几乎为0.0 的权重。

换言之，该结点被赋给与观测点一致的值。

这就是一个准确插值。

距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。

用距离倒数格网化时可以指定一个圆滑参数。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 克里格方法依赖于数学模型和统计模型，正是 由于引入了包括概率模型在内的统计模型，使 克里格方法与确定性插值方法区分开来。在克 里格方法中预测的结果将与概率联系在一起， 即用克里格方法进行插值，一方面能生成预测 表面，一方面能给出预测值的误差。
• 由于建立在统计学的基础上，因此不仅可 以产生预测曲面，而且可以产生误差和不 确定性曲面，用来评估预测结果的好坏
最近邻法评价
• 特征：用泰森多边形插值方法得到的结果图变化只发生在
边界上，在边界内都是均质的和无变化的；
• 适用于较小的区域内，变量空间变异性也不很明显的情况。
符合人思维习惯，距离近的点比距离远的点更相似，对插 值点的影响也更明显；
• 最近邻法插值的优点是不需其他前提条件，方法简单，效
率高；
• 缺点是受样本点的影响较大，只考虑距离因素，对其他空
（2）“实际”验证
将部分已知变量值的样本点作为“训练数据集”，用于插值 计算；另一部分样点 “验证数据集”，该部分站点不参加 插值计算。然后利用“训练数据集” 样点进行内插，插值 结果与“训练数据集”验证样点的观测值对比，比较插值的 效果。
插值方法
1. 最近邻法(Nearest Neighbor) 2. 算术平均值(Arithmetic Mean) 3. 距离反比法(Inverse Distance) 4. 高次曲面插值(Multiquadric) 5. 趋势面插值(Polynomial) 6. 最优插值(Optimal) 7. 样条插值(Spline Surface) 8. 径向基函数插值(Radial Basis Functions) 9. 克里金插值(Kriging) 10. 最小曲率 (Minimum Curvature)
三、距离反比法(Inverse Distance)
距离反比插值方法最早由 Shepard 提出(Richard Franke,1982)提出的，并逐步得到发展。每个采样对 插值结果的影响随距离增加而减弱，因此距目标点近的样 点赋予的权重较大。
•
距离倒数乘方格网化方法是一个加权平均插值法，可以进 行确切的或者圆滑的方式插值。方次参数控制着权系数如何 随着离开一个格网结点距离的增加而下降。对于一个较大的 方次，较近的数据点被给定一个较高的权重份额，对于一个 较小的方次，权重比较均匀地分配给各数据点。计算一个格 网结点时给予一个特定数据点的权值与指定方次的从结点到 观测点的该结点被赋予距离倒数成比例。当计算一个格网结 点时，配给的权重是一个分数，所有权重的总和等于1.0。 当一个观测点与一个格网结点重合时，该观测点被给予一个 实际为 1.0 的权重，所有其它观测点被给予一个几乎为 0.0 的权重。换言之，该结点被赋给与观测点一致的值。这就是 一个准确插值。距离倒数法的特征之一是要在格网区域内产 生围绕观测点位置的"牛眼"。用距离倒数格网化时可以指定 一个圆滑参数。大于零的圆滑参数保证，对于一个特定的结 点，没有哪个观测点被赋予全部的权值，即使观测点与该结 点重合也是如此。圆滑参数通过修匀已被插值的格网来降低" 牛眼"影响。
权重系数 wj 一般由下式给出： wj f d ej
f (d
i 1
n
ej
)
其中 n 是已知点数， f d ej

表示对于插值点(xe, ye) 的权重函数。
d ej 与已知点 (xj,, yj ) 之间距离
f d ej 最常用的一种形式是：
1 f d ej b d ej
局部内插法
局部内插法只使用邻近的数据点来估计未知点的值，步骤如 下： • 定义一个邻域或搜索范围； • 搜索落在此邻域范围的数据点； • 选择能表达这有限个点空间变化的数学函数； • 为未知的数据点赋值。 局部内插方法： • 样条函数插值法 • 距离倒数插值 • Kriging插值（空间自由协方差最佳内插） • …… • 单个数据点的改变只影响其周围有限的数据点。
间因素和变量所固有的某些规律没有过多地考虑。实际应 用中，效果常不十分理想。
二、算术平均值(Arithmetic Mean)
算术平均值方法以区域内所有测值的平均值来估计插值点 的变量值(Creutin, 1982)。
算术平均值法评价
算术平均值的算法比较简单，容易实现。但只考虑算术 平均，根本没有顾及其他的空间因素，这也是其一个致命的 弱点，因而在实际应用中效果不理想。
• 多种 kriging 方法
3、精确插值和近似插值
• 精确插值：产生通过所有观测点插值等 于估计值。
• 近似插值：插值产生的曲面不通过所有观测 点。
• 当数据存在不确定性时，应该使用近似插值，由 于估计值替代了已知变量值，近似插值可以平滑 采样误差。
⑤ 可视化、可操作性（插值软件选择）：三维的透视图等。
插值验证
（1） 交叉验证 交叉验证法（cross－validation），首先假定每一测点 的要素值未知，而采用周围样点的值来估算，然后计算所有 样点实际观测值与内插值的误差，以此来评判估值方法的优 劣。 各种插值方法得到的插值结果与样本点数据比较。
公式
其数学表达式为：
v e vi vi 表示 i 点的变量值。 其中ve 表示待估点变量值，
i 点必须满足如下条件：
d ei min( d e1 , d e 2 , d en )
d ij xi x j y i y j
2
其中
2
表示点 i(xi, yi)与点 j(xj, yj)间的欧几里德距离。
距离反比插值公式
其数学表达式为： ve
w
j 1
n
j
vj
其中 v e（j=1,…, n）是点（xj , yj ）的 变量值，wj 是其对应的权重系数
权重系数wj的计算是关键问题，不同类型距离反比法的差别 就是权重系数的计算公式不同，因而最后的插值结果也有细 微的差别。
距离反比权重系数的确定
• 反距离权重插值综合了泰森多边形的自然邻近法和多元回归渐变 方法的长处，在插值时为待估点Z值为邻近区域内所有数据点都 的距离加权平均值，当有各向异性时，还要考虑方向权重。 • 权重函数与待估点到样点间的距离的U次幂成反比，即随着距离 增大，权重呈幂函数递减。且对某待估点而言，其所有邻域的样 点数的权重和为1。 • 决定反距离权重插值法结果的参数包括距离的U次幂值的确定， 同时还取决于确定邻近区域的所使用的方法。此外，为消除样点 数据的不均匀分布的影响，还可设置引入一个平滑参数，以保证 没有哪个样点被赋予全部的权重，即使得插值运算时尽可能不只 有一个样点参与运算。 • IDW是一种全局插值法，即全部样点都参与某一待估点的Z值的 估算； • IDW的适用于呈均匀分布且密集程度足以反映局部差异的样点数 据集； • IDW与之前介绍的插值法的不同之处在于，它是一种精确的插值 法，即插值生成的表面中预测的样点值与实测样点值完全相等。
b 是合适的常数。当 b 取值为 1 或 2 时，对应的是距离倒数插值和 距离倒数平方插值。b 也可以对不同的已知点选择不同的值，即 bj 。
距离反比插值评价
• 优点——简便易行；可为变量值变化很大的数据集提 供一个合理的插值结果；不会出现无意义的插值结果 而无法解释。
• 不足——对权重函数的选择十分敏感；易受数据点集 群的影响，结果常出现一种孤立点数据明显高于周围 数据点的“鸭蛋”分布模式； • 全局最大和最小变量值都散布于数据之中。 • 距离反比很少有预测的特点，内插得到的插值点数据 在样点数据取值范围内。
n
高次曲面插值评价
• 高次曲面插值根据变量值已知点和变量值未知点的坐标所 构成的圆锥，进行插值，为从离散点构建一个连续的表面 提供了一个比较优秀的插值方法。
• 由于在计算权重系数时需要已知点的距离矩阵及其逆矩阵， 因而当数据点增多时，矩阵及其逆的求解都比较费时。
五、趋势面分析
• 通常把实际的地理曲面分解为趋势面和剩余面两部分，前 者反应地理要素的宏观分布规律，属于确定性因素作用的 结果；而后者则对应于微观区域，被认为是随机因素影响 的结果。 • 趋势面分析的一个基本要求就是，所选择的趋势面模型应 该是剩余值最小，而趋势值最大，这样拟合度精确度才能 达到足够的准确性。 • 趋势面分析是通过回归分析原理，运用最小二乘法拟合一 个二维非线性函数，模拟地理要素在空间上的分布规律， 展示地理要素在地域空间上的变化趋势。 • 在数学上，拟合数学曲面要注意两个问题：一是数学曲面 类型（数学表达式）的确定，二是拟合精度的确定。
空间插值 Spatial Interpolation
• 空间插值的概念 • 空间插值的类型 • 空间插值的方法
空间插值概念
空间插值——空间插值常用于将离散点的测量数据转换为连 续的数据曲面，以便与其它空间现象的分布模式进行比较， 它包括了空间内插和外推两种算法。空间内插算法：通过已 知点的数据推求同一区域未知点数据。空间外推算法：通过 已知区域的数据，推求其它区域数据。
一般插值过程
① 内插方法（模型）的选择； ② 空间数据的探索性分析，包括对数据的均值、方 差、协方差、独立性和变异函数的估计等；
③ 进行内插；
④ 内插结果评价； ⑤ 重新选择内插方法，直到合理；
⑥ 内插生成最后结果。
插值方法选择的原则
① 精确性：
② 参数的敏感性：许多的插值方法都涉及到一个或多个参数， 如距离反比法中距离的阶数等。有些方法对参数的选择相当 敏感，而有些方法对变量值敏感。后者对不同的数据集会有 截然不同的插值结果。希望找到对参数的波动相对稳定，其 值不过多地依赖变量值的插值方法。 ③ 耗时：一般情况下，计算时间不是很重要，除非特别费时。 ④ 存储要求：同耗时一样，存储要求不是决定性的。特别是在 计算机的主频日益提高，内存和硬盘越来越大的情况下，二 者都不需特别看重。
2、确定性方法和地统计方法 确定性方法