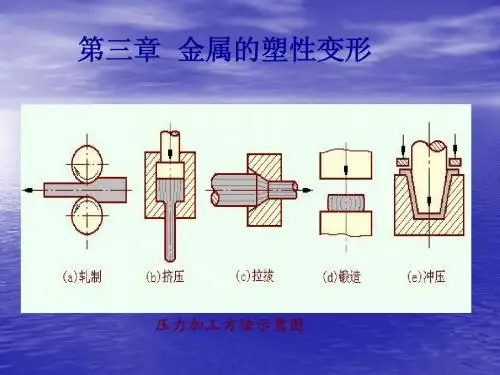
二、金属的塑性变形材料受力后要发生变形，变形可分为三个阶段：弹性变形；弹－塑性变形；断裂。
外力较小时产生弹性变形，外力较大时产生塑性变形，而当外力过大时就会发生断裂。
在整个变形过程中，对材料组织、性能影响最大的是弹－塑性阶段的塑性变形部分。
如：锻造、轧制、拉拔、挤压、冲压等生产上的许多加工方法，都要求使金属产生变形，一方面获得所要求的形状及尺寸，另一方面可引起金属内部组织和结构的变化，从而获得所要求的性能。
因此研究塑性变形特征与组织结构之间相互关系的规律性，具有重要的理论和实际意义。
弹性变形(Elastic Deformation)1.1 弹性变形特征(Character of Elastic Deformation)1．变形是可逆的；2．应力与应变保持单值线性函数关系，符合Hooke定律：σ＝Eε，τ＝Gγ，G＝E/2(1-ν) 3．弹性变形量随材料的不同而异。
1.2 弹性的不完整性(Imperfection of Elastane)工程上应用的材料为多晶体，内部存在各种类型的缺陷，弹性变形时，可能出现加载线与卸载线不重合、应变的发展跟不上应力的变化等现象，称为弹性的不完整性，包括包申格效应、弹性后效、弹性滞后等。
1．包申格效应(Bauschinger effect)现象：下图为退火轧制黄铜在不同载荷条件下弹性极限的变化情况。
曲线A：初次拉伸曲线，σe＝240Pa曲线B：初次压缩曲线，σe＝178Pa曲线C：B再压缩曲线，σe↑，σe＝278Pa曲线D：第二次拉伸曲线，σe↓，σe＝85Pa可见：B、C为同向加载，σe↑；C、D为反向加载，σe↓。
定义：材料经预先加载产生少量塑性变形,然后同向加载则σe升高，反向加载则σe降低的现象，称为包申格效应。
对承受应变疲劳的工件是很重要的。
2．弹性后效(Anelasticity)理想晶体(Perfect crystals)：实际金属(Actual metal)：弹性后效示意图这种在弹性极限范围内，应变滞后于外加应力，并和时间有关的现象称为弹性后效。
3．弹性滞后(Elastic hysteresis)由于应变落后于应力，在σ－ε曲线上使加载线与卸载线不重合而形成一封闭回线，称为弹性滞后。
弹性滞后表明：加载时消耗于材料的变形功大于卸载时材料恢复所释放的变形功，多余的部分被材料内部所消耗，称为内耗，大小＝弹性滞后环面积。
实际应用的金属材料有的要求高内耗，有的要求低内耗，如制作钟、乐器的材料，乐器低内耗，消振能力低，声音好听；制作机座、汽轮机叶片的材料，要求高内耗，以消除振动。
金属的塑性变形机理金属一般是由无数单个晶粒构成的多晶体。
要了解晶体的塑性变形机理必须先了解单个晶粒或单晶体的塑性变形机制。
塑性变形时变形体在外力的作用下，其大量原子群多次地、定向的从一个稳定平衡位置转移到另一个平衡位置，在宏观上便产生不能恢复的塑性变形。
在常温和低温下，单晶体的塑性变形主要通过滑移、孪生和扭折等方式进行。
1．滑移(Slipping)在切应力作用下，晶体的一部分沿着一定晶面（滑移面）和一定晶向（滑移方向）相对另一部分发生相对位移的现象。
←ττ→完整晶体滑移特点(Characteristics)：1) 滑移后，晶体的点阵类型不变；2) 晶体内部各部分位向不变；3) 滑移量是滑移方向上原子间距的整数倍；4) 滑移后，在晶体表面出现一系列台阶。
滑移系(Slip Systems)：滑移是沿着滑移面和滑移方向进行的，滑移面和滑移方向往往是金属晶体中原子排列最密的晶面和晶向，因为原子密度最大的晶面其面间距最大，点阵阻力小，因而容易沿着这些发生滑移；滑移方向为原子浓度最大的方向是由于最密排方向上的原子间距最短，位错b最小。
一个滑移面和此面上的一个滑移方向合起来称为一个滑移系。
可用{hkl}<uvw>来表示。
可见：构成滑移系必须满足两条，1)必须是密排面和密排方向；2)向一定在面上。
实验表明：滑移系越多，滑移越容易，塑性越好。
BCC与FCC的滑移系数相同，但滑移方向对塑性变形的作用比滑移面大，所以FCC的塑性比BCC的塑性好。
如Cu的塑性比α－Fe好。
滑移的临界分切应力(Critical resolved shear stressof slipping)：不是有切应力作用就能产生滑移，只有在滑移面上沿滑移方向的分切应力达到一定值时，才能发生滑移。
能引起滑移的最小分切应力称为临界分切应力，用τk表示。
设单晶体中只有一组滑移面，试样横截面积为A，轴心拉力为F，滑移面的法线与F夹角为φ，滑移方向与F的夹角为λ，滑移面面积Aˊ＝A/cosφ。
外力在滑移面上沿滑移方向的切向分力为：Fτ＝Fcosλ外力在滑移方向上的分切应力：τ=Fτ/ Aˊ= Fcosλ/( A/cosφ)=Fcosλcosφ/AF/A＝σ，当滑移系中的分切应力达到其临界分切应力值而开始滑移时，σ＝σS，此时τ＝τk，所以τk＝σS cosλcosφ cosλcosφ称为取向因子。
单向拉伸(Simple rension)：当外力与滑移面平行（φ＝90°）或垂直（λ＝90°）时，取向因子最小，σS为无限大，不可能产生滑移，此时的位向称为硬位向；当外力与滑移面和滑移方向的夹角都接近45°时，取向因子最大，σS最小，容易滑移，此时的位向称为软位向。
滑移时晶面的转动(Therotary of crystal face in the slipping)：单晶体滑移时，除滑移面发生相对位移外，还伴随着晶面的转动。
拉伸时，晶体转动力求使滑移系转到与力轴平行的方向；压缩时，晶体转动力求使滑移系转到与力轴垂直的方向。
由于晶体的转动，使原来有利于滑移的晶面滑移到一定程度后，变成不利于滑移的晶面；而原来不利于滑移的晶面，则可能转到有利于滑移的方向上，参与滑移。
所以，滑移可在不同的滑移系上交替进行，其结果造成晶体的均匀变形。
2．孪生(Twinning)在切应力作用下，晶体的一部分以一定的晶面（孪生面）为对称面和一定的晶向（孪生方向）与另一部分发生相对切变的现象。
特点(Characteristics)：1) 点阵类型不变但晶体位向发生变化，呈镜面对称；2) 孪生是一种均匀切变，每层原子面的位移量与该原子面到孪生面的距离成正比，其相邻原子面的相对位移量相等，且小于一个原子间距，即孪生时切变量是原子间距的分数倍；3) 孪生变形速度很快，接近声速。
滑移与孪生的区别(Distinction between slipping and twinning)：晶体位向位移量切应力塑变量变形速度滑移不变整数倍小大慢孪生改变分数倍大小快从而可促进滑移产生。
相同点：切应力作用产生、点阵不变、位错运动来实现。
3．扭折(Kink)对那些既不能进行滑移也不能进行孪生的地方，为了使晶体的形状与外力相适应，当外力超过某一临界值时晶体将会产生局部弯曲，这种变形方式称为扭折。
见图4.20，变形区域称为扭折带。
ABCD区域的点阵发生了扭曲，其左右两侧区域则发生了弯曲。
扭折是一种协调性变形，它能引起应力松弛，使晶体不致断裂。
扭折后，晶体取向与原取向不再相同，有可能使该区域内的滑移系处于有利取向，而发生滑移。
多晶体的塑性变形(Plastic deformation of polycrystals)多晶体是由许多大小、外形和取向不同的晶粒组成的，晶粒与晶粒之间存在着晶界，晶界上的原子排列不同于晶内，不规则，这样使多晶体的变形较单晶体变形复杂得多，下面分别加以讨论。
1．晶界在变形中的作用(Action of grain-boundary in the deformation)主要作用是提高变形抗力。
比如：两个晶粒构成的试样，做拉伸实验时，试样往往呈竹节状，晶界处较粗，变形小，因为晶界上原子排列紊乱，是杂质原子或各种缺陷集中的地方，使该处在滑移时，位错运动的阻力较大，难以发生变形。
2．晶粒在变形中的作用(Action of grain in the deformation)÷反映在晶粒大小对变形的影响上。
多晶体的屈服强度σS与晶粒平均直径d的关系可用著名的霍尔－佩奇（Hall-Petch）公式表示：σS＝σ0＋Kd-1/2式中，σ0反映晶内对变形的阻力，相当于单晶体的屈服强度；K反映晶界对变形影响系数，与晶界结构有关。
霍尔－佩奇公式适应性甚广。
①亚晶粒大小或者是两相片状组织的层片间距对屈服强度的影响；②塑性材料的流变应力与晶粒大小之间的关系；③脆性材料的脆断应力与晶粒大小之间的关系；④金属材料的疲劳强度、硬度与其晶粒大小之间的关系，都可用霍尔－佩奇公式来表达。
由此可见：σS∝d-1/2即d↓，σS↑。
实验表明：晶粒越细，不仅强度高，而且塑韧性也好。
强度高，是因为晶粒细，单位面积上的晶粒数多，晶界的总面积大，每个晶粒周围不同取向的晶粒数多，对塑性变形的抗力大；塑韧性好，是因为晶粒细，单位体积中的晶粒数越多，变形可在更多的晶粒中发生，且比较均匀，减少了应力集中，使金属发生很大的塑性变形也不断裂。
3．多晶体的塑性变形过程(Process of plastic deformation of polycrystals)多晶体是由单晶体组成的，在同样的外力作用下，不同晶粒滑移系上的切应力不一样，处于软位向的首先开始滑移，如：A晶粒，它周围的晶粒B、C处于硬位向，未发生塑性变形，只能以弹性变形来协调已变形晶粒A，因而限制了A的继续发展；当外力进一步增加时，位错在A晶粒晶界附近堆积，这样就产生了应力集中，达到一定程度时，变形就会越过晶界，传到它附近的晶粒B、C中，A晶粒也可能发生转动，转到硬位向，不再继续变形，另一批B、C晶粒开始发生变形。
总之，多晶体塑性变形总是一批一批晶粒逐步地发生，从少量晶粒开始逐步扩大到大量的晶粒，从不均匀变形逐步发展到比较均匀的变形。
特点：①各晶粒变形的不同时性；②各晶粒变形的相互协调性。
合金的塑性变形(Plastic deformation of alloy)合金是在纯金属的基础上又加入其它元素，使相结构发生了变化，也改变了基体金属的变形抗力，使强度、硬度提高，塑韧性降低。
按合金组成相不同，主要可分为单相固溶体合金和多相合金，它们的塑性变形具有不同的特点。
1. 单相固溶体合金的塑性变形(Plastic deformation of single-phase solid solution alloy)与纯金属相比其区别在于单相固溶体合金中存在溶质原子。
溶质原子对合金、塑性变形的影响主要表现在固溶强化作用上。
固溶强化：溶质原子的存在及其固溶度的增加，使基体金属的变形抗力提高。
2. 多相合金的塑性变形(Plastic deformation of multiphase alloy)多相合金与单相固溶体合金的不同之处是除基体相外，还有第二相存在，第二相的数量、尺寸、形状和分布不同，使多相合金的塑性变形更加复杂。
