齿轮传动EHL油膜厚度的计算_李锡玖

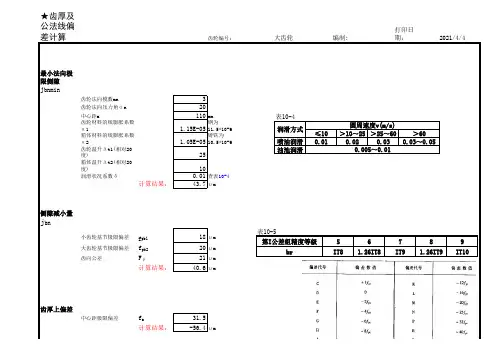
齿轮侧隙最简单的计算方法
齿轮侧隙是指齿轮齿面之间的间隙，是齿轮传动中的重要参数之一。

其计算方法如下：
1. 确定齿轮的模数m和齿数z。

2. 计算齿面高度系数ha和齿根高度系数hf。

齿面高度系数ha和齿根高度系数hf的计算公式如下：
ha = 2.25 / m
hf = 1.25 / m
3. 计算齿面厚度系数Cf和齿根厚度系数Cp。

齿面厚度系数Cf和齿根厚度系数Cp的计算公式如下：
Cf = 0.167 + 0.0333 * (z / 10)
Cp = Cf - ha
4. 计算齿轮侧隙J。

齿轮侧隙J的计算公式如下：
J = 0.3 * (Cf + Cp)
其中，J的单位为毫米。

以上是齿轮侧隙最简单的计算方法，但实际应用中还需要考虑齿轮的精度等因素。

齿轮设计计算说明书齿轮是一种常见的传动装置，广泛应用于机械设备中。

齿轮设计计算是指根据传动比、输入输出转速和所需扭矩等参数，计算出齿轮的模数、齿数、齿宽等具体尺寸。

齿轮设计计算的目的是确保齿轮系统具有良好的传动效率和耐久性，提高整个机械设备的性能和可靠性。

齿轮设计计算一般包括以下几个方面的内容：1. 计算传动比：传动比是指输入输出转速之间的比值，一般用来确定主动齿轮和从动齿轮的齿数。

传动比的计算公式为：传动比 = 输出转速 / 输入转速2. 计算齿轮模数：齿轮模数是齿轮齿廓尺寸的一个重要参数，直接影响到齿轮的传动效率和工作寿命。

齿轮模数的计算公式为：模数 = 齿轮齿数 / 齿轮直径模数的选取通常是根据齿轮材料的强度、传动功率等要求来确定的。

3. 计算齿数：齿数是齿轮设计中最为重要的参数之一，齿数的选择直接影响到齿轮的传动性能。

齿轮齿数的计算公式为：输入齿数 = 输出齿数 * 传动比在实际设计中，一般通过选择整数齿数或特定齿数的齿轮来满足传动比的要求。

4. 计算齿宽：齿宽是指齿轮的轴向长度，也是齿轮设计中一个重要的参数。

齿宽的计算公式为：齿宽 = 模数 * 齿数齿宽的选取通常是根据传动功率的大小和齿轮的强度要求来确定的。

5. 计算齿轮的模型参数：通过齿轮的模数、齿数、齿宽等尺寸参数，可以计算出齿轮的其他模型参数，如：齿顶高、齿根高、齿顶圆直径等。

以上是齿轮设计计算的一些基本内容，设计人员还需要根据具体的应用要求，考虑其他因素，如齿轮传动的噪声、振动、磨损等，并结合实际情况进行调整和优化。

齿轮设计计算需要考虑多个参数，需要设计人员有扎实的数学基础和专业知识，以确保设计出合理的齿轮系统。

在实际应用中，也可以借助专业的齿轮设计软件进行计算和验证，以提高设计的准确性和效率。

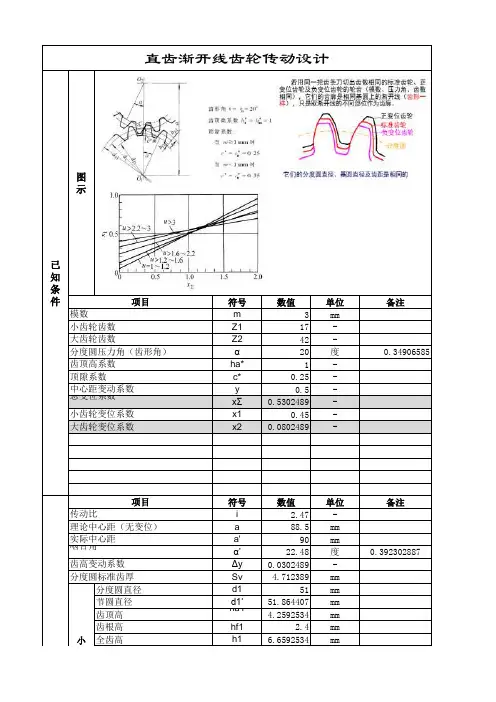
齿轮计算公式节圆柱上的螺旋角：L d /tan 00⋅=πβ 基圆柱上的螺旋角：n g αββcos sin sin 0⋅= 齿厚中心车角：Z θ/90︒= 销子直径：m 728.1dp ⋅=中心距离增加系数：)1cos /(cos )2/)((y b 021-⋅+=ααZ Z标准正齿轮的计算（小齿轮①，大齿轮②）1． 齿轮齿 标准 2． 工齿齿形 直齿 3． 模数 m 4． 压力角 c αα=0 5． 齿数 21,Z Z6． 有效齿深 m 2h e ⋅=7． 全齿深 c m h +=28． 齿顶隙 m 35.0,m 25.0,m 2.0c ⋅⋅⋅=9． 基础节圆直径 m d 0⋅=Z 10． 外径 m )2(d k ⋅+=Z 11． 齿底直径 c 2m )2(d r ⋅-⋅-=Z12． 基础圆直径 0g cos m d αZ ⋅⋅= 13． 周节 m t 0⋅=π 14． 法线节距 0e cos m t απ⋅⋅= 15． 圆弧齿厚2/m S 0⋅=π16． 弦齿厚)2sin(m S 1j Z πZ ⋅⋅⋅= 17． 齿轮油标尺齿高 m m h j +Z⋅-⨯⋅Z =)2cos1()2/(π18． 跨齿数5.0)180/(0m ⨯⋅=Z αZ19． 跨齿厚 ])5.0([cos 0o m inva m m S Z ⨯-⋅Z ⋅⋅=πα20． 销子直径 m 728.1d ⋅=21． 圆柱测量尺寸 d m d m +⋅Z =)cos /cos (0φα （偶数齿）d )]90(cos)cos /cos m [(d 0m +︒⨯⋅=ZφαZ （奇数齿）其中, 00)2cos (1απαφinv m d inv +-⋅Z 22． 齿隙f ?移位正齿轮计算公式（小齿轮①，大齿轮②）1． 齿轮齿形 转位 2． 工具齿形 直齿 3． 模数 m 4． 压力角 c αα=05． 齿数 Z6． 有效齿深 m 2h e ⋅=7． 全齿深 c m )]x x (y 2[h 21+⋅⋅-+= 或 c m 2h +⋅=8． 齿隙 c 9． 转位系数 x10． 中心距离 m y x ⋅+=αα11． 基准节圆直径m d 0⋅=Z12． 啮合压力角021210b inv )x x (tan 2inv αZ Z αα+++⋅=13． 啮合节圆直径)(x 2d 211b Z Z Z α+⋅⋅=14． 外径 m )x y (2m )2(d 21k ⋅-⋅+⋅+=Z15． 齿顶圆直径 h 2d d 1k r ⋅-=16． 基圆直径 0cos t g m d α⋅⋅Z = 17． 周节 m t 0⋅=π 18． 法线节距00cos m t απ⋅⋅=19． 圆弧齿厚 010tan m x 22mS απ⋅⋅⋅⋅⋅=20． 弦齿厚)tan x 2x 2sin(m S 1111j Z απZ ⋅⋅+⋅⋅⋅=21． 齿轮游标尺齿高2d d )]tan x 22cos(1[2mh 110k10111j -+⋅⋅+⋅-⋅⋅=Z αZ πZ 22． 跨齿数 5.0180x 1b m 1+⋅=αZ23． 跨齿厚 01m sin m x 2）(S 1α⋅⋅⋅+=标准齿轮的齿厚 24． 梢子直径m 728.1d 1⋅=25． 圆柱测量尺寸11cos cos 1d m d m +⋅⋅Z =φα （偶数齿）1110)90cos(cos cos 1d m d m +Z ︒⋅⋅⋅Z =φα （奇数齿）1010101i 1tan x 2)inv 2(cos m d inv Z ααZ παZ Φ⋅⋅+-⋅-⋅⋅=标准螺旋齿的计算公式（齿直角方式）（小齿轮①，大齿轮②）1. 齿轮齿形 标准2. 齿形基准断面 齿直角3. 工具齿形 螺旋齿4. 模数 n c m m =5. 压力角 n 0c ααα==6. 齿数 1Z7. 螺旋角方向 0β（左或右）8. 有效齿深 n e m 2h ⋅=9.全齿深c m 2h n +⋅=10. 正面压力角n1s cos m tan βZ α⋅=11. 中心距离n21cos 2m )(βZ Z α⋅⋅+=12. 基准节圆直径n10cos m d βZ ⋅=13. 外径 n 01k m 2d d ⋅+= 14. 齿底圆直径 )c m (2d d n 01r ++= 15. 基圆直径gnn 1g cos cos m d 1βαZ ⋅⋅=16. 基圆上的螺旋角 n 0g cos sin sin αββ⋅= 17. 导程1001cot d L 1βπ⋅⋅=18. 周节（齿直角）n n 0m t ⋅=π19. 法线节距（齿直角） n n en cos m t απ⋅⋅= 20. 圆弧齿厚（齿直角） 2m S nn 0⋅=π21. 相当正齿轮齿数101cos βZ Z =22. 弦齿厚)2sin(m S 1v n 1v j 1Z πZ ⋅⋅⋅=23. 齿轮游标尺齿深n 1v n1v 1j m )2cos 1(2m h +⋅-⋅⋅=Z πZ24. 跨齿数 5.01801v n m 1+⋅=Z αZ25. 跨齿厚]inv )5.0m ([cos m S s 11n n m 1αZ Z πα⋅+-⋅⋅⋅=26. 梢子直径)2(cos 1111n v n v n inv inv m d απφα-Z ⋅+⋅Z ⋅=其中，)(2tan 11Rad inv n v n απαφ-Z ⋅+=27. 圆柱测量尺寸11cos cos 1d m d m +⋅⋅Z =φα （偶数齿）1110)90cos(cos cos 1d m d m +Z ︒⋅⋅⋅Z =φα （奇数齿）10101011tan 2)2(cos Z ⋅⋅+-Z ⋅-⋅⋅Z =ααπαφx inv m d inv i 28. 齿隙f移位螺旋齿的计算公式（齿直角方式）（小齿轮①，大齿轮②）1. 齿轮齿形 移位2. 齿形基准断面 齿直角3. 工具齿形 螺旋齿4. 模数（齿直角） n c m m =5. 压力角（齿直角） 0a a a c n -=6. 齿数 1Z7. 螺旋方向 0β8. 有效齿深 n e m h 2= 9. 全齿深 c m h n +=2 10. 移位系数 1n x11. 中心距离n x ym a a +=12. 正面模数0cos βns m m =13. 正面压力角0cos tan βans m =14. 相当正齿轮齿数311βϑs z z v =15. 齿直角啮齿压力角an v v n n ann a inv z z x x b inv +++=2121t an 216. 基准节圆直径11cos βno m z d =17. 外径n n n nk m x m m z d 101122cos ++=β18. 啮齿节圆直径)(22111z z z a d x b +=19. 基圆直径gnn g a m z d βcos cos 11⋅=20. 基础圆柱上的螺旋角 n o g a cos sin sin ββ=21. 圆弧齿厚 n n n on m a x s ⋅⋅+=)tan 22(1π22. 弦齿厚 )t an 22sin(11111v on v n v j z a x z m z s ⋅+⋅⋅=π23. 齿轮游标尺齿高2)}t an 22cos(1{21111111o k v o n v n v d d z a x z m z hj -+⋅+-⋅=π24. 跨齿数 5.018011+=v n m z ab z25. 跨齿厚111sin 2n n n m a m x s ⋅⋅+=）（标准螺旋齿轮的齿厚 26. 销子直径 近似值=1d27. 圆柱测量尺寸/1111cos cos d a m z d ss m +⋅=φ（偶数齿）/1111190cos cos cos d z a m z d s s m +⋅= φ111111tan 2)2(cos z a x inva z a m z d in n n s n n ⋅+--='πφ 注：齿隙f=m 1.25以下 0.025-0.075m 1.25-2.5 0.05-0.10))*25.2((tan 2)2(cos 22111111m r r L z a x inva z a m z d in n n s n n ---⋅+--='πφ。

齿轮参数计算公式
齿轮是机械传动中常用的元件，用于将动力传递给其他机械部件。

在设计和计算齿轮系统时，需要考虑一些参数，以确保齿轮的正常运转和传动效率。

以下是一些常用的齿轮参数计算公式。

1. 齿轮模数（Module）：齿轮的模数是齿轮齿数与齿轮的分度圆直径之比。

模数的计算公式为：M = D / Z，其中M为模数，D为齿轮的
分度圆直径，Z为齿轮的齿数。

2. 齿轮轮齿高度（Tooth Height）：齿轮的轮齿高度是齿轮的齿顶到齿谷的距离。

轮齿高度的计算公式为：H = 2.25 * M，其中H为轮齿高度，M为模数。

3. 齿轮齿顶高度（Addendum）：齿轮的齿顶高度是齿顶到分度圆的距离。

齿顶高度的计算公式为：A = M，其中A为齿顶高度，M为模数。

4. 齿轮齿根高度（Dedendum）：齿轮的齿根高度是齿根到分度圆的距离。

齿根高度的计算公式为：B = 1.25 * M，其中B为齿根高度，M
为模数。

5. 齿轮齿宽度（Face Width）：齿轮的齿宽度是齿轮齿条的宽度。

齿宽度的计算公式为：F = K * M，其中F为齿宽度，K为齿宽系数，
通常取1.5-2。

6. 齿轮模数和齿数的关系：齿轮的模数和齿数是相互关联的。

齿数的计算公式为：Z = π * D / M，其中Z为齿数，D为齿轮的分度圆直径，M为模数。

以上是齿轮参数计算的一些常用公式，根据具体的设计要求和传动需求选择合适的参数，可以确保齿轮的正常工作和传递效率。

在实际应用中，还需要考虑齿轮的强度、齿面硬度等参数，以满足设计要求和使用条件。

齿轮尺寸计算《齿轮尺寸计算》
一、螺旋齿轮尺寸计算
1、计算齿轮模数：
齿轮模数＝齿轮外径÷齿数。

2、计算齿轮基圆：
齿轮基圆＝模数×齿数。

3、计算齿顶圆：
齿顶圆＝齿轮基圆＋2×模数。

4、计算齿根圆：
齿根圆＝齿轮基圆－2×模数。

5、计算齿宽：
齿宽＝模数×0.7071。

二、圆柱齿轮尺寸计算
1、计算齿轮模数：
齿轮模数＝齿轮外径÷齿数。

2、计算齿厚：
齿厚＝模数÷2。

3、计算齿顶圆半径：
齿顶圆半径＝模数×0.5。

4、计算齿根圆半径：
齿根圆半径＝模数×0.5。

三、立锥齿轮尺寸计算
1、计算齿轮模数：
齿轮模数＝齿轮顶径÷齿数。

2、计算齿厚：
齿厚＝模数÷2。

3、计算齿根母线夹角：
齿根母线夹角＝180°÷齿数＋顶隙角度。

4、计算齿顶面夹角：
齿顶面夹角＝180°÷齿数－顶隙角度。

5、计算齿宽：
齿宽＝模数×0.5。

内啮合齿轮参数计算已知：m＝2.5、Z1＝15、Z2＝19、α0＝28°、ha*＝1.0、C*＝0.25、π＝3.14159 分度圆d1＝m×Z1＝37.5 mm （外齿轮）d 2＝m×Z2＝47.5 mm （内齿轮）基圆d b1＝m×Z1×cosα0＝33.1105 mmd b2＝m×Z2×cosα0＝41.9400 mm基节t b1＝t b2＝π×m×cosα0＝6.9346 mm齿顶高ha1＝ha*×m＝2.5 mmha2＝ha*×m＝2.5 mm齿根高h f1＝(ha*＋C*)m＝3.125 mmh f2＝(ha*＋C*)m＝3.125 mm齿顶圆直径 da1＝d1＋2 ha1＝42.5 mmda2＝d2－2 ha2＋Δda＝42.9949 mmΔda＝2 ×ha*2×m÷Z2÷tgα0齿根圆直径d f1＝d1－2 h f1＝31.25 mmd f2＝d2＋2 h f2＝53.75 mm全齿高h1＝ha1＋h f1＝5.625 mmh 2＝（d f2－da2）÷2＝5.375 mm齿顶圆压力角αa1＝arccos(d b1÷da1)＝38.824442°αa2＝arccos(d b2÷da2)＝12.718233°重合度ε＝(1÷2π)×[Z1 (tgαa1－tgα0) －Z2 (tgαa2－tgα0)]＝1.577 中心距a＝m÷2×（Z2－Z1）÷2＝5 mm齿顶厚Sα1＝da1×(π÷2÷Z1＋invα0－invαa1)＝0.8724 mmSα2＝da2×(π÷2÷Z2－invα0－invαa2)＝1.5452 mm齿顶厚对应角度αd1＝360÷(da1×π÷Sα1)＝2.352229°αd2＝360÷(da2×π÷Sα2)＝4.118326°分度圆弧齿厚S1＝m×(π÷2)＝3.927 mmS 2＝m×(π÷2)＝3.927 mm公法线长W1＝m×cosα0×[π×(K1－0.5)＋Z1×invα0]＝18.7609 mm W2＝m×cosα0×[π×(K2－0.5)＋Z2×invα0]＝19.1408 mm K1＝Z×α0÷180＋0.5＝2.833 K2＝Z×α0÷180＋0.5＝3.455K: 四舍五入取整数。

弹性流体动压（力）润滑（Elastohydrodynamic Lubrication ，EHL ）弹性流体动力润滑是研究在相互滚动或滚动伴有滑动的两个弹性物体之间的流体动力润滑问题。

大部分的机械运动副，载荷是通过较大的支承面来传递的。

如滑轨、滑动轴承等。

其单位面积受的压力比较小，通常为1～100×105Pa 。

另一些运动副是通过名义上的线接触或点接触来传递载荷的，如齿轮、滚动轴承等。

因接触面积很小，平均单位面积压力很大，接触处的压力可达109Pa 以上。

在这种苛刻条件下，用古典润滑理论计算的油膜厚度与实际情况不符。

与古典理论不一致的原因是：⑴高的压力使油的粘度增大；已不是雷诺方程中假定的“粘度在间隙中保持不变”。

⑵重载使弹性体发生显著的局部变形，也不是雷诺方程假定的“两个固体表面是刚性的”。

由于上述两个效应，剧烈地改变了油膜的几何形状，而油膜形状又反过来影响接触区的压力分布。

因此，解决弹流润滑问题必须同时满足流体润滑方程和固体弹性方程。

凡表面弹性变形量与最小油膜厚度处在同一量级的润滑问题，都属于弹流问题。

3.1刚性滚动体的动压润滑①简化问题在分析齿轮、短圆柱滚子轴承等问题时，常用如图9所示两个圆柱的接触。

从图9（a ）中可得：0h h BC FE =++式中：h 位于x 处的油膜厚度； h 0 最小油膜厚度。

o 1当1ϕ很小时，1ϕ≈1x R ，略去1ϕ2以上的高次项，得：2211122x BC R R ϕ==同理，得则：2012112x h h R R ⎛⎫=++ ⎪⎝⎭如将圆柱对圆柱简化为圆柱对平面，如图9（b ）所示。

设：当量圆柱体的半径11211R R R -⎛⎫=+ ⎪⎝⎭ 。

（即：12111R R R =+）则：202x h h R=+②求解油膜压力与最小油膜厚度的关系假定（在载荷较小的时候可这样假定）： ⑴滚动体是刚性的，不考虑接触变形；⑵润滑油（流体）是等粘度的，粘度不随压力而变化； ⑶滚动体相对于油膜厚度为无限长，即不考虑润滑油有垂直于画面的法向流动。