齿轮传动强度计算例题01

齿轮传动例1 二级圆柱齿轮减速器，其中一级为直齿轮，另一级为斜齿轮。

试问斜齿轮传动应置于高速级还是低速级？为什么？若为直齿锥齿轮和圆柱齿轮组成减速器，锥齿轮传动应置于高速级还是低速级？为什么？答：在二级圆柱齿轮传动中，斜齿轮传动放在高速级，直齿轮传动放在低速级。

其原因有三点：1）斜齿轮传动工作平稳，在与直齿轮精度等级相同时允许更高的圆周速度，更适于高速。

2）将工作平稳的传动放在高速级，对下级的影响较小。

如将工作不很平稳的直齿轮传动放在高速级，则斜齿轮传动也不会平稳。

3）斜齿轮传动有轴向力，放在高速级轴向力较小，因为高速级的转矩较小。

由锥齿轮和斜齿轮组成的二级减速器，一般应将锥齿轮传动放在高速级。

其原因是：低速级的转矩较大，齿轮的尺寸和模数较大。

当锥齿轮的锥距R 和模数m 大时，加工困难，制造成本提高。

例3 一对闭式直齿圆柱齿轮传动，已知：z 1= 25，z 2 = 75，m = 3 mm ，d φ= 1，小齿轮的转速 n =970 r/min 。

主从动轮的][H σ 1 = 690 MPa ，][H σ 2 = 600 MPa ，载荷系数K = 1.6， 节点区域系数Z H = 2.5，材料弹性系数Z E = 189.8 MPa ，重合度系数εZ =0.9，是按接触疲劳强度，求该齿轮传动传递的功率。

提示：接触疲劳强度校核公式为][ )1(2211H H E H ubd u KT Z Z Z σσε≤+=解：由已知条件：u = z 2 / z 1 = 75/25 = 3d 1 = m z 1 = 3×25 = 75 mm b =φd d 1 = 1×75 = 75 mm因为大齿轮的许用接触应力较低，故按大齿轮计算承载能力：)1(2][21221+⋅⎪⎪⎭⎫ ⎝⎛=u K u bd ZZ Z T E H H εσ )13(6.12375759.08.1895.260022+⨯⨯⨯⨯⋅⎪⎭⎫⎝⎛⨯⨯== 195182 Nmm = 195.182 Nm 齿轮传动所能传递的功率为：=⨯⨯=⋅=30970182.1953011ππn T P 19826 W = 19.826 kW例4图示双级斜齿圆柱齿轮减速器，高速级：mn=2 mm ，z 1=22，z 2 =95，︒=20n α，a =120，齿轮1为右旋；低速级：mn= 3 mm ，z 3 =25，z 4=79，︒=20n α，a =160。

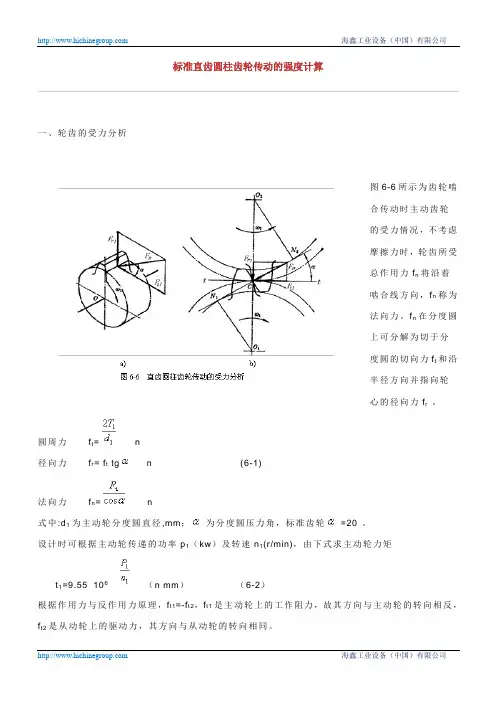
标准直齿圆柱齿轮传动的强度计算一、轮齿的受力分析图6-6所示为齿轮啮合传动时主动齿轮的受力情况，不考虑摩擦力时，轮齿所受总作用力f n将沿着啮合线方向，f n称为法向力。

f n在分度圆上可分解为切于分度圆的切向力f t和沿半径方向并指向轮心的径向力f r 。

圆周力f t=n径向力 f r= f t tg n (6-1)法向力 f n=n式中:d1为主动轮分度圆直径,mm；为分度圆压力角，标准齿轮=20°。

设计时可根据主动轮传递的功率p1（kw）及转速n1(r/min)，由下式求主动轮力矩t1=9.55×106×（n mm）（6-2）根据作用力与反作用力原理，f t1=-f t2，f t1是主动轮上的工作阻力，故其方向与主动轮的转向相反，f t2是从动轮上的驱动力，其方向与从动轮的转向相同。

同理，f r1=-f r2，其方向指向各自的轮心。

二、载荷与载荷系数由上述求得的法向力f n 为理想状况下的名义载荷。

由于各种因素的影响，齿轮工作时实际所承受的载荷通常大于名义载荷，因此，在强度计算中，用载荷系数k 考虑各种影响载荷的因素，以计算载荷f nc 代替名义载荷f n 。

其计算公式为(6-3)式中：k 为载荷系数，见表6-3。

表6-3 载荷系数k二、齿根弯曲疲劳强度计算齿根处的弯曲强度最弱。

计算时设全部载荷由一对齿承担，且载荷作用于齿顶，将轮齿看作悬臂梁，其危险截面可用30o 切线法确定，即作与轮齿对称中心线成30o 夹角并与齿根过渡曲线相切的两条直线，连接两切点的截面即为齿根的危险截面，如图6-7所示。

运用材料力学的方法，可得轮齿弯曲强度校核的公式为= ≤或σf =≤（6-4）或由上式得计算模数m的设计公式m≥ (6-5)式中:=b/d1称齿宽系数（b为大齿轮宽度），由表6-4查取；称为齿形系数，由图6-8查取；[]为弯曲许用应力，由式6-8计算。

表6-4齿宽系数=b/d1三、齿面接触疲劳强度计算齿面接触疲劳强度计算是为了防止齿间发生疲劳点蚀的一种计算方法，它的实质是使齿面节线处所产生的最大接触应力小于齿轮的许用接触应力，齿面接触应力的计算公式是以弹性力学中的赫兹公式为依据的，对于渐开线标准直齿圆柱齿轮传动，其齿面接触疲劳强度的校核公式为≤或≤ (6-6)将上式变换得齿面接触疲劳强度的设计公式d1≥ (6-7)式中：“±”分别用于外啮合、内啮合齿轮；z e为齿轮材料弹性系数，见表6-5；z h为节点区域系数，标准直齿轮正确安装时z h =2.5；[σh]为两齿轮中较小的许用接触应力，由式6-9计算；u为齿数比，即大齿轮齿数与小齿轮齿数之比。

直齿轮传动设计计算实例直齿轮传动设计计算实例已知条件：斜齿圆柱齿轮传动，输入功率为PI =4.17kw，齿轮转速为nI=626r/min，传动比为i2=3.7，由电动机驱动，工作寿命为10年，每年工作300天，每天工作16小时，轻微冲击，转向不变。

1、齿轮基本参数选定（齿轮设计参照《机械设计》教材进行设计）（1）运输机为一般工作机器，速度不高，故选用8级精度。

（2）材料：参照表10-1高速级小齿轮选用45#钢调质处理，齿面硬度为250HBS。

高速级大齿轮选用45#钢调质，齿面硬度为220HBS。

（3）小齿轮齿数初选为，大齿轮齿数。

2、按齿面接触强度计算由设计计算公式（10-9a）进行计算，即（1）确定公式内的各计算数据①试选载荷系数②计算小齿轮传递的转矩③由表10-7选取齿宽系数④由表10-6查得材料的弹性影响系数⑤由图10-21d按齿面硬度查得小齿轮的接触疲劳强度极限，大齿轮的接触疲劳强度极限⑥由式10-13计算应力循环次数。

⑦由图10-19取接触疲劳寿命系数。

⑧计算接触疲劳许用应力取失效概率为1％，安全系数S=1，由式（10-12）得﹙2﹚计算①试算小齿轮分度圆直径,代入中最小值。

②计算圆周速度v③计算齿宽b④计算齿宽与齿高之比模数齿高⑤计算载荷系数根据，8级精度，由图10-8查得动载荷系数；直齿轮,；由表10-2查得使用系数；由表10-4用插值法查得8级精度、小齿轮相对支承非对称布置时，。

由，查图得；故载荷系数⑥按实际的载荷系数校正所算得的分度圆直径，由式（10-10a）得⑦计算模数m3、按齿根弯曲强度设计由式（10-5）得弯曲强度的设计公式为（1）确定公式内的各计算数值①由图10-20c查得小齿轮的弯曲疲劳强度极限，大齿轮的弯曲疲劳强度极限；②由图10-18取弯曲疲劳寿命系数,；③计算弯曲疲劳许用应力取弯曲疲劳安全系数S=1.3，由式(10-12)得④计算载荷系数K⑤查取齿形系数由表10-5查得⑥查取应力校正系数由表10-5查得⑦计算大、小齿轮的并加以比较故小齿轮的数值较大。

齿轮传动设计计算的步骤(1)根据题目提供的工作情况等条件，确定传动形式，选定合适的齿轮材料和热处理方法，查表确定相应的许用应力。

(2)分析失效形式，根据设计准则，设计m或d1;(3)选择齿轮的主要参数；(4)计算主要集合尺寸，公式见表9-2.表9T0或表971;(5)根据设计准则校核接触强度或弯曲强度；(6)校核齿轮的圆周速度，选择齿轮传动的静的等级和润滑方式等；(7)绘制齿轮零件工作图。

以下为设计齿轮传动的例题：例题试设计一单级直齿圆柱齿轮减速器中得齿轮传动。

已知：用电动机驱动，传递功率P=10KW,小齿轮转速n1=950r/min,传动比i=4,单向运转，载荷平稳。

使用寿命10年，单班制工作。

解：(1)选择材料与精度等级小轮选用45钢，调质,硬度为229〜286HBs (表9-4)大轮选用45钢，正火，硬度为169〜217HBs(表9-4)。

因为是普通减速器，由表973 选IT8级精度。

因硬度小于350HBS,属软齿面，按接触疲劳强度设计，再校核弯曲疲劳强度。

(2)按接触疲劳强度设计①计算小轮传递的转矩为T. =9.55X106— =9.55X106 X —=105N • mmL 1nl 950查表9-5取③齿数Z 和齿宽系数〃. 取z1=25,则z2 = izl =4x25 = 100因单级齿轮传动为对称布置，而齿轮齿面又为软齿面，由表972选 取〃广1。

④许用接触应力【0〃】 由图979 (c)查得=57。

河&6nm 2 = 53OMP”由9-7表查得SH=1N| =60nJLh = 60x955乂 10x52x5x8)= 1.19xl09N,=M = 30= 3x1(/i 4查图 978 得Zw = l, Z N 2 = L08 由式(9-13)可得O H 1 = Z M P 〃皿=122Z2 = 570MPaS H 1= Z N 2 sM2 = 108x530 = 572 4”所S a查表9-6得Z/=189.8西西，故由式(9-14)得71.1X 1O 5X 5 f 3.52x189.8 Y\ 1x4 [ 570 J〃？=必=tLl = 2.296mm 乙25 由表97取标准模数m=2. 5mm"1.1=57.4mmd 1 = mzl = 2.5x25 = 62.5mmd2 = mz2 = 2.5x100 = 250mmb = y/ • d\X62.5 = 62.5〃〃〃圆整后取b2=65mm。

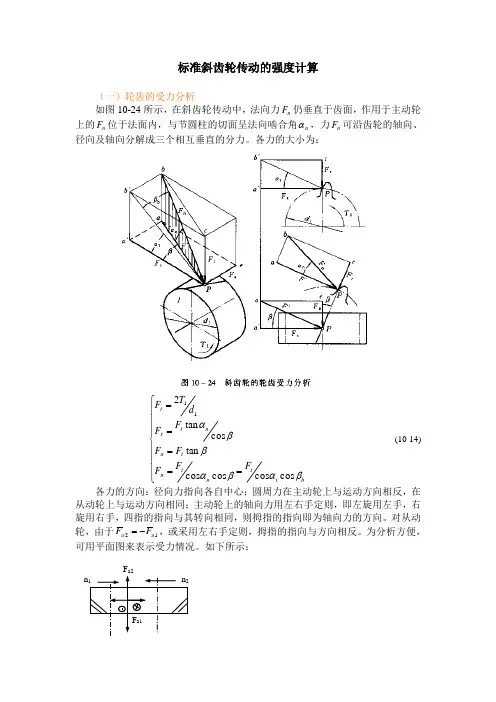
标准斜齿轮传动的强度计算（一）轮齿的受力分析如图10-24所示，在斜齿轮传动中，法向力n F 仍垂直于齿面，作用于主动轮上的n F 位于法面内，与节圆柱的切面呈法向啮合角n α，力n F 可沿齿轮的轴向、径向及轴向分解成三个相互垂直的分力。

各力的大小为：⎪⎪⎪⎩⎪⎪⎪⎨⎧=====b t t n t n t a n t r tF F F F F F F d T F βαβαββαcos cos cos cos tan cos tan 211 (10-14) 各力的方向：径向力指向各自中心；圆周力在主动轮上与运动方向相反，在从动轮上与运动方向相同；主动轮上的轴向力用左右手定则，即左旋用左手，右旋用右手，四指的指向与其转向相同，则拇指的指向即为轴向力的方向。

对从动轮，由于12a a F F -=，或采用左右手定则，拇指的指向与方向相反。

为分析方便，可用平面图来表示受力情况。

如下所示：n 1 n 2F r1 F r2F a1 F a2F a1从上面的计算知：轴向力a F 与βtan 成正比，为不使轴承承受大的轴向力，β不宜过大，一般︒=12~8β；人字齿有两个轴向力且大小相等，方向相反，故可取较大值，一般︒=40~15β。

（二）计算载荷由于轮齿上的计算载荷与啮合区的实际接触线的长度有关，在斜齿轮的轮齿上啮合线为斜线，且可能有几对齿同时啮合，故接触线的总长为所有啮合齿上接触线的长度之和，这个总和可用βεαcos b 来表示。

因此， t t b t bt n ca b KF b KF L KF p αεβαβεααcos cos cos cos === (10-15) αε为端面重合度，可按图10-26查取。

斜齿轮的纵向重合度可用如下公式计算：()βφπβεβtan 318.0sin 1Z m b d n ==计算载荷系数βαK K K K K v a =，各系数的查取可参考直齿轮。

（三）齿根弯曲强度的计算如右图所示，斜齿轮齿面上的接触线为一斜线。

直齿圆柱齿轮传动的强度计算齿面接触强度计算闭式齿轮传动的主要失效形式之一是齿面点蚀，故需进行齿面接触疲劳强度计算。

齿面的 疲劳点蚀与齿面接触应力有关，齿面的最大接触应力可用赫兹公式计算如下：222121211111E E bF n H μμρρπσ-+-±⋅=式中 Fn 为法向力；b 为两轮齿的接触宽度；E1,E2为两齿轮材料的弹性模量；12,μμ为两齿轮材料的泊松比；12,ρρ为两齿面接触点处的曲率半径；“+”号用于外啮合，“一”号用于内啮合。

前已述及，齿根部分靠近节线处最易发生点蚀，故常取节点处的接触应力为计算依据。

由图11．4，a 可知，节点处的齿廓曲率半径为111sin 2N C d αρ==111sin 2N C d αρ==取传动比i=z 2/z 1≥l ，式中z 2为大齿轮齿数，z 1为小齿轮齿数，则12(1)ad i =±方向相同。

径向力F ，6勺方向由作用点指向轮心。

2.计算载荷上述的法向力Fn 为名义载荷。

理论上Fn 应沿齿宽均匀分布，但由于轴和轴承的变形，传动装置的制造，安装误差等原因，载荷沿齿宽的分布并不是均匀的，因此会出现载荷集中现象。

如图9．29所示，齿轮位置对轴承不对称时，由于轴的弯曲变形齿轮将互相倾斜，这时，轮齿左端载荷增大。

轴和轴承的刚度越小，齿宽B 越宽，载荷集中越严重。

此外，由于各种原动机和工作机特性不同，齿轮制造误差以及轮齿变形等原因，还会引起附加动载荷。

精度越低，圆周速度越高，附加动载荷就越大。

因此，计算齿轮强度时，通常用计算载荷KFn 代替名义载荷Fn ，以考虑载荷集中和附加动载荷的影响。

其中K 为载荷系数，其值可由表9．6查取。

图9．29 载荷集中现象表9.6 载荷系数K9．11．2 载荷计算1．受力分析在图9．30中，当不计齿面间的摩擦力时，作用于主动轮齿上的总压力将垂直于齿面，即为图中法向力芦n 。

芦n 可分解为圆周力F ，和径向力芦r 。

1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中，由于赫兹应力是齿面间应力的主要指标，故把赫兹应力作为齿面接触应力的计算基础，并用来评价接触强度。

齿面接触疲劳强度核算时，根据设计要求可以选择不同的计算公式。

用于总体设计和非重要齿轮计算时，可采用简化计算方法；重要齿轮校核时可采用精确计算方法。

分析计算表明，大、小齿轮的接触应力总是相等的。

齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。

实际使用和实验也证明了这一规律的正确。

因此，在齿面接触疲劳强度的计算中，常采用节点的接触应力分析齿轮的接触强度。

强度条件为：大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力，即：⑴圆柱齿轮的接触疲劳强度计算1）两圆柱体接触时的接触应力在载荷作用下，两曲面零件表面理论上为线接触或点接触，考虑到弹性变形，实际为很小的面接触。

两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。

两圆柱体接触，接触面为矩形（2axb），最大接触应力σHmax位于接触面宽中线处。

计算公式为：接触面半宽:最大接触应力:•F——接触面所受到的载荷•ρ——综合曲率半径，（正号用于外接触，负号用于内接触）•E1、E2——两接触体材料的弹性模量•μ1、μ2——两接触体材料的泊松比2）齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况，都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。

在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。

节点附近处的ρ虽然不是最小值，但节点处一般只有一对轮齿啮合，点蚀也往往先在节点附近的齿根表面出现，因此，接触疲劳强度计算通常以节点为最大接触应力计算点。

参数直齿圆柱齿轮斜齿圆柱齿轮节点处的载荷为综合曲率半径为接触线的长度为，3）圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式，并考虑各载荷系数的影响，得到：接触疲劳强度的校核公式为：接触疲劳强度的设计公式为：•KA——使用系数•KV——动载荷系数•KHβ——接触强度计算的齿向载荷分布系数•KHα——接触强度计算的齿间载荷分配系数•Ft——端面内分度圆上的名义切向力，N；•T1——端面内分度圆上的名义转矩，N.mm；•d1——小齿轮分度圆直径，mm；•b ——工作齿宽，mm，指一对齿轮中的较小齿宽；•u ——齿数比；•ψd——齿宽系数，指齿宽b和小齿轮分度圆直径的比值（ψd=b/d1）。

§11—3 齿轮传动的精度GB规定：齿轮精度等级有12个按GB10095-88（圆柱齿轮）和GB11365-89（圆锥齿轮）规定：精度等级：高→低1，2，3，4，5，6，7，8，9，10，11，12常用齿轮公差分三个组，反映：传递运动的准确性——第Ⅰ公差组；传动的平稳性——第Ⅱ公差组；载荷分布的均匀性——第Ⅲ公差组；另外考虑齿侧间隙：制造误差、轮齿变形、受热膨胀、便于润滑→14种齿厚偏差精度等级选择，按圆周速度V、用途、工作条件和传动功率来确定，可参考表11-2§11—4 直齿圆柱齿轮传动的作用力及计算载荷一、受力分析忽略摩擦力，法向力F n沿啮合线作用于节点处（将分布力简化为集中力）F n与过节点P的圆周切向成角度α。

F n可分解为F t和F r1、力的大小圆周力F t=2T/d1F t1=-F t2径向力F r=F t tg αF r1=-F r2 大小相等，方向相反法向力F n=F t / cos αF n1=-F n2T1——小齿轮上传递的扭矩Nmm d1—小齿轮上的直径mm, α=20°2、力的方向F t——“主反从同”F r——指轮心齿面接触线上的法向载荷F n——名义载荷（未计及载荷波动，载荷沿齿宽方向的不均匀性和轮齿齿廓曲线误差等）二、计算载荷；KF n载荷系数：K=K A Kν KβKα表11-3K A——工作情况系数Kν——载荷系数Kβ——齿向载荷分布系数Kα——齿间载荷分配系数1、工作情况系数K A考虑了齿轮啮合时，外部因素引起的附加动载荷对传动的影响，它与原动机与工作机的类型与特性，联轴器类型等有关2、动载荷系数Kν——考虑齿轮制造误差和装配误差及弹性变形等内部因素引起的附加动载荷的影响3、齿向载荷分布系数K——考虑轴的弯曲、扭转变形、轴承、支座弹β性变形及制造和装配误差而引起的沿齿宽方向载荷分布不均匀的影响。

4、齿间载荷分配系数K——考虑同时有多对齿啮合时各对轮齿间载荷α分配不均匀的系数。

例 1 设计用于带式输送机传动装置的闭式单级直齿圆柱齿轮传 动。

传递功率 P=2.7kW ，小齿轮转速 n 1=350r/min ，传动比 i=3.57。

输送机工作平稳，单向运转，两班工作制，齿轮对称布置，预期寿命 10 年，每年工作 300天。

解： 1. 选择齿轮精度等级、材料、齿数1）带式输送机属于一般机械，且转速不高，故 初选择 8 级精度。

2）因载荷平稳，传递功率较小，可采用软齿面齿轮。

参考表 5-6， 小齿轮选用 45 钢调质处理，齿面硬度 220~250HBS ，σHLim1 =595MPa ， σ FE1=230MPa ；大齿轮选用 45 钢正火处理，齿面硬度 170~200HBS ， σ HLim2 =520MPa ，σ FE2=200MPa 。

3）初选小齿轮齿数 z 1=24，则 z 2=iz 1=3.57×24=85.68，取 z 2=87。

故实际传动比 i=z 2/ z 1=87/ 24=3.62，与要求的传动比 3.57的误差小于 3%。

对于齿面硬度小于 350 HBS 的闭式软齿面齿轮传动，应按齿面 接触强度设计，再按齿根弯曲强度校核。

2. 按齿面接触强度设计1）查表 5-8，原动机为电动机， 工作机械是输送机， 且工作平稳， 取载荷系数 K=1.2。

2）小齿轮传递的转矩T19550 P 9550 2.7 73.671N m 1 n 1 350设计公式 5-48 d 12000KT 1 2u 1 Z E Z H Z3）查表5-13，齿轮为软齿面，对称布置，取齿宽系数φd=14）查表 5-10，两齿轮材料都是锻钢，故取弹性系数 Z E =189.8 MPa 1/2。

5）两齿轮为标准齿轮，且正确安装，故节点区域系数 Z H =2.5，取重合度系数 Z ε=0.96）计算许用接触应力HHLimZ N Z W Z XSH① 应力循环次数小齿轮 N 1=60n 1jL h =60×350×1×(2×8×300×10)=10.08 ×108 大齿轮 N 2= N 1/i=10.08×108/ 3.62=2.78×108② 据齿轮材料、热处理以及 N 1、N 2，查接触疲劳寿命系数图表，不允许出现点蚀，得接触疲劳寿命系数 软齿面故 ZW=1，ZX=1 。

第四章齿轮传动计算题专项训练〔答案〕；1、一标准直齿圆柱齿轮的齿数z=36，顶圆d；2、一标准直齿圆柱齿轮副，其传动比i=3，主；3、有一对标准直齿圆柱齿轮，m=2mm，α=20；4、某传动装置中有一对渐开线；5、一对正确安装的标准渐开线正常齿轮的ɑ=2；解:144=4/2(Z1+iZ1)Z1=18Z2；d1=4*18=72d2=4*54=216第四章齿轮传动计算题专项训练〔答案〕1、一标准直齿圆柱齿轮的齿数 z=36，顶圆da=304mm。

试计算其分度圆直径d、根圆直径df、齿距p以及齿高h。

2、一标准直齿圆柱齿轮副，其传动比i=3，主动齿轮转速n1=750r/min，中心距a=240mm，模数m=5mm。

试求从动轮转速n2，以及两齿轮齿数z1和z2。

3、有一对标准直齿圆柱齿轮， m=2mm，α=200，Z1=25，Z2=50，求〔1〕如果n1=960r/min，n2=？〔2〕中心距a=？〔3〕齿距p=？答案：n2=480a=754、某传动装置中有一对渐开线。

标准直齿圆柱齿轮〔正常齿〕，大齿轮已损坏，小齿轮的齿数z1=24，齿顶圆直径da1=78mm,中心距a=135mm,试计算大齿轮的主要几何尺寸及这对齿轮的传动比。

解：78=m(24+2)m=3a=m/2(z1+z2)135=3/2(24+z2)z2=66da2=3*66+2*3=204i5、一对正确安装的标准渐开线正常齿轮的ɑ=200，m=4mm，传动比i12=3，中心距a=144mm。

试求两齿轮的齿数、分度圆半径、齿顶圆半径、齿根圆半径。

解:144=4/2(Z1+iZ1)Z1=18Z2=3*18=54d1=4*18=72d2=4*54=216da1=72+2*4=80ra1=(72+2*4)/2=40da 2=216+2*4=224ra2=(216+2*4)/2=112df1=72-2*1,25*4=62rf1=(72-2*1,25*4)/2=31df2=216-2*1,25*4=206rf2=(216-2*1,25*4)/2=1036、一对外啮合标准直齿圆柱齿轮传动的标准中心距a＝150mm，传动比i12=4,小齿轮齿数Z1=20。

1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效，应进行齿面接触疲劳强度计算。

因此，齿轮接触疲劳强度计算准则为：齿面接触应力σH小于或等于许用接触应力σHP，即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区，轮齿受力较大，故点蚀首先出现在节点附近。

因此，通常计算节点的接触疲劳强度。

图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。

为了简化计算，用一对轴线平行的圆柱体代替它。

两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径，如图b所示。

由弹性力学可知，当一对轴线平行的圆柱体相接触并受压力作用时，将由线接触变为面接触，其接触面为一狭长矩形，在接触面上产生接触应力，并且最大接触应力位于接触区中线上，其数值为式中σH-接触应力〔Mpa〕Fn-法向力〔N〕L-接触线长度〔mm〕rS-综合曲率半径〔mm〕；±-正号用于外接触，负号用于内接触ZE-材料弹性系数〔〕，，其中E1、E2分别为两圆柱体材料的弹性模量〔MPa〕；m1、m2分别为两圆柱体材料的泊松比。

上式说明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同，且靠近节点的齿根处最大〔图c、d〕。

但为了简化计算，通常控制节点处的接触应力。

节点处的参数〔1〕综合曲率半径由图可知，，代入rE公式得式中：，称为齿数比。

对减速传动，u=i；对增速传动，u=1/i。

因，则有〔2〕计算法向力〔3〕接触线长度L引入重合度系数Ze，令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令，称为节点区域系数。

则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数，并将代入上式，则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径〔mm〕；ZE-材料弹性系数()，按下表查取；注：泊松比m1＝m2＝0.3Z H-节点区域系数，考虑节点处轮廓曲率对接触应力的影响，可由下左图查取。