下载文档原格式
第一章绪论1-1．研究误差的意义是什么？简述误差理论的主要内容。
答：研究误差的意义为：(1）正确认识误差的性质,分析误差产生的原因,以消除或减小误差；（2）正确处理测量和实验数据，合理计算所得结果，以便在一定条件下得到更接近于真值的数据;（3)正确组织实验过程,合理设计仪器或选用仪器和测量方法,以便在最经济条件下，得到理想的结果。
误差理论的主要内容:误差定义、误差来源及误差分类等。
1—2．试述测量误差的定义及分类，不同种类误差的特点是什么？答:测量误差就是测的值与被测量的真值之间的差；按照误差的特点和性质,可分为系统误差、随机误差、粗大误差.系统误差的特点是在所处测量条件下，误差的绝对值和符号保持恒定，或遵循一定的规律变化（大小和符号都按一定规律变化）；随机误差的特点是在所处测量条件下，误差的绝对值和符号以不可预定方式变化；粗大误差的特点是可取性。
1-3．试述误差的绝对值和绝对误差有何异同，并举例说明。
答：(1）误差的绝对值都是正数，只是说实际尺寸和标准尺寸差别的大小数量，不反映是“大了”还是“小了”,只是差别量；绝对误差即可能是正值也可能是负值,指的是实际尺寸和标准尺寸的差值。
+多少表明大了多少,—多少表示小了多少。
（2)就测量而言,前者是指系统的误差未定但标准值确定的，后者是指系统本身标准值未定. 1-6．在万能测长仪上,测量某一被测件的长度为 50mm，已知其最大绝对误差为 1μm,试问该被测件的真实长度为多少？已知：L＝50，△L＝1μm＝0。
001mm，解: 绝对误差＝测得值－真值，即：△L＝L－L＝L－△L＝50－0.001＝49.999（mm）测件的真实长度Ｌ1—7．用二等标准活塞压力计测量某压力得 100。
2Pa，该压力用更准确的办法测得为100。
5Pa，问二等标准活塞压力计测量值的误差为多少?解:在实际检定中，常把高一等级精度的仪器所测得的量值当作实际值。
故二等标准活塞压力计测量值的误差＝测得值－实际值，即：100.2－100。
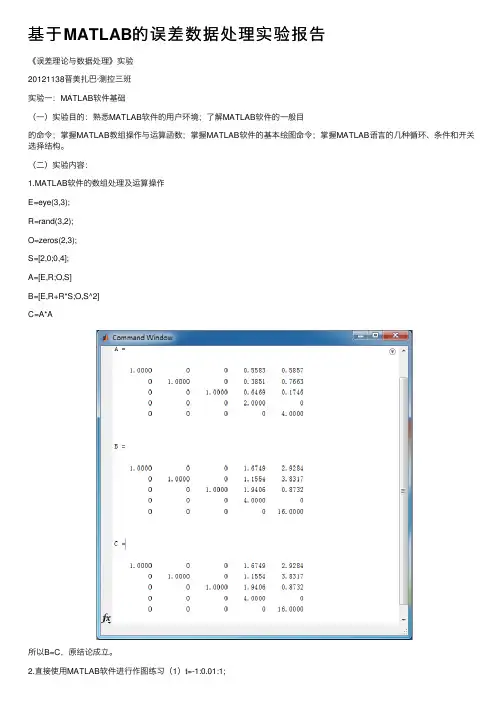
基于MATLAB的误差数据处理实验报告《误差理论与数据处理》实验20121138晋美扎巴·测控三班实验⼀：MATLAB软件基础（⼀）实验⽬的：熟悉MATLAB软件的⽤户环境；了解MATLAB软件的⼀般⽬的命令；掌握MATLAB教组操作与运算函数；掌握MATLAB软件的基本绘图命令；掌握MATLAB语⾔的⼏种循环、条件和开关选择结构。
（⼆）实验内容：1.MATLAB软件的数组处理及运算操作E=eye(3,3);R=rand(3,2);O=zeros(2,3);S=[2,0;0,4];A=[E,R;O,S]B=[E,R+R*S;O,S^2]C=A*A所以B=C，原结论成⽴。
2.直接使⽤MATLAB软件进⾏作图练习（1）t=-1:0.01:1;x=sin(2*pi*t);y=cos(2*pi*10*t);plot(t,x,t,y)xlabel('t');ylabel('函数值')legend('正弦函数','余弦函数')（2）1) x=-10:0.01:10; y=normpdf(x,0,1); plot(x,y)（3）[x,y]=meshgrid(-10:0.05:10);z=sin(pi*sqrt(x.^2+y.^2));mesh(x,y,z);3.⽤MATLAB语⾔编写命令M-⽂件和函数M-⽂件a=input('请输⼊a的值')x0=a./2x1=(x0+a./x0)./2while(abs((x0-x1)>1e-5))x0=x1;x1=(x0+a./x0)./2;enddigits(8)vpa(x1)实验⼆：测量数据的统计分析（⼀）实验⽬的：通过对测量数据进⾏统计分析，学习掌握测量数据统计分析的基本⽅法。
（⼆）实验内容：1.>> x=normrnd(10,5,500,1);>> mu=mean(x)mu =9.7672>> sigma=std(x)sigma =4.8754>> va=var(x)va =23.7697>> hist(x)>> y=normpdf(x,mu,sigma); >> plot(x,y)2. x=-15:0.01:15; y1=normpdf(x,0,1); y2=normpdf(x,0,4); y3=normpdf(x,10,1); plot(x,y1,y2,y3);3.>> x=randn(500,1);>> mu=mean(x);>> va=var(x);>> cs=skewness(x);>> ck=kurtosis(x);>> hist(x);>> sigma=std(x);>> y=normpdf(x,mu,sigma); >> plot(x,y) >> cscs =0.1117>> ckck =3.0089>> mumu =0.0730>> vava=0.99814. >> x=-5:0.1:5; >> y1=tpdf(x,5); >> y2=tpdf(x,10); >> y3=tpdf(x,20); >> z=normpdf(x,0,1); >>plot(x,y1,x,y2,x,y3,x,z)5.>> x=0:0.2:30; >> y1=chi2pdf(x,5); >> y2=chi2pdf(x,10); >> y3=chi2pdf(x,20); >>plot(x,y1,x,y2,x,y3)6.x=0:0.01:10;y1=fpdf(x,4,5);y2=fpdf(x,10,20);y3=fpdf(x,50,50); plot(x,y1,x,y2,x,y3)实验三：等精度和⾮等精度直接测量数据处理（⼀）实验⽬的：通过本实验使学⽣掌握等精度和⾮等精度直接测量数据的基本处理⽅法；学习如何发现和处理测量列中的随机误差、系统误差和粗⼤误差，如何科学地表达测量结果。
误差理论与大数据处理作业本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March第一章绪论1-1．研究误差的意义是什么？简述误差理论的主要内容。
答：研究误差的意义为：(1)正确认识误差的性质，分析误差产生的原因，以消除或减小误差；(2)正确处理测量和实验数据，合理计算所得结果，以便在一定条件下得到更接近于真值的数据；(3)正确组织实验过程，合理设计仪器或选用仪器和测量方法，以便在最经济条件下，得到理想的结果。
误差理论的主要内容：误差定义、误差来源及误差分类等。
1-2．试述测量误差的定义及分类，不同种类误差的特点是什么？答：测量误差就是测的值与被测量的真值之间的差；按照误差的特点和性质，可分为系统误差、随机误差、粗大误差。
系统误差的特点是在所处测量条件下，误差的绝对值和符号保持恒定，或遵循一定的规律变化（大小和符号都按一定规律变化）；随机误差的特点是在所处测量条件下，误差的绝对值和符号以不可预定方式变化；粗大误差的特点是可取性。
1-3．试述误差的绝对值和绝对误差有何异同，并举例说明。
答：(1)误差的绝对值都是正数，只是说实际尺寸和标准尺寸差别的大小数量，不反映是“大了”还是“小了”，只是差别量；绝对误差即可能是正值也可能是负值，指的是实际尺寸和标准尺寸的差值。
+多少表明大了多少，-多少表示小了多少。
(2)就测量而言,前者是指系统的误差未定但标准值确定的，后者是指系统本身标准值未定。
1-6．在万能测长仪上，测量某一被测件的长度为 50mm，已知其最大绝对误差为 1μm，试问该被测件的真实长度为多少？已知：L＝50，△L＝1μm＝0.001mm，解：绝对误差＝测得值－真值，即：△L＝L－L＝L－△L＝50－0.001＝49.999（mm）测件的真实长度Ｌ1-7．用二等标准活塞压力计测量某压力得 100.2Pa，该压力用更准确的办法测得为100.5Pa，问二等标准活塞压力计测量值的误差为多少解：在实际检定中，常把高一等级精度的仪器所测得的量值当作实际值。
第一章绪论1-1．研究误差的意义是什么？简述误差理论的主要内容。
答：研究误差的意义为：(1)正确认识误差的性质，分析误差产生的原因，以消除或减小误差；(2)正确处理测量和实验数据，合理计算所得结果，以便在一定条件下得到更接近于真值的数据；(3)正确组织实验过程，合理设计仪器或选用仪器和测量方法，以便在最经济条件下，得到理想的结果。
误差理论的主要内容：误差定义、误差来源及误差分类等。
1-2．试述测量误差的定义及分类，不同种类误差的特点是什么？答：测量误差就是测的值与被测量的真值之间的差；按照误差的特点和性质，可分为系统误差、随机误差、粗大误差。
系统误差的特点是在所处测量条件下，误差的绝对值和符号保持恒定，或遵循一定的规律变化（大小和符号都按一定规律变化）；随机误差的特点是在所处测量条件下，误差的绝对值和符号以不可预定方式变化；粗大误差的特点是可取性。
1-3．试述误差的绝对值和绝对误差有何异同，并举例说明。
答：(1)误差的绝对值都是正数，只是说实际尺寸和标准尺寸差别的大小数量，不反映是“大了”还是“小了”，只是差别量；绝对误差即可能是正值也可能是负值，指的是实际尺寸和标准尺寸的差值。
+多少表明大了多少，-多少表示小了多少。
(2)就测量而言,前者是指系统的误差未定但标准值确定的，后者是指系统本身标准值未定。
1-6．在万能测长仪上，测量某一被测件的长度为 50mm，已知其最大绝对误差为 1μm，试问该被测件的真实长度为多少？已知：L＝50，△L＝1μm＝0.001mm，解：绝对误差＝测得值－真值，即：△L＝L－L＝L－△L＝50－0.001＝49.999（mm）测件的真实长度Ｌ1-7．用二等标准活塞压力计测量某压力得 100.2Pa，该压力用更准确的办法测得为100.5Pa，问二等标准活塞压力计测量值的误差为多少？解：在实际检定中，常把高一等级精度的仪器所测得的量值当作实际值。
故二等标准活塞压力计测量值的误差＝测得值－实际值，即：100.2－100.5＝－0.3（ Pa）第二章 误差的基本性质与处理2-1．试述标准差 、平均误差和或然误差的几何意义。
误差理论——静态误差理论及数据处理综合应用报告静态误差理论及数据处理综合应用报告摘要：通过观察物理现象，定量测量，并对测量结果进行分析，从而实现对物理规律的认识和证实。
在进行实验测量时，产生误差是不可避免的。
因此，必须借助于误差理论，研究、估计和评判测量的数据和测量结果是否准确可靠，并应采取正确的数据处理方法，以便在一定条件下得到更接近于真值的数据。
本课题主要分为，测量与误差、误差的合成与分配、测量的不确定度评定、数据处理方法几部分。
在误差的合成与分配中，分析了多个测量量误差与总体误差之间的关系。
在测量的不确定度评定中，进行了误差与不确定度之间的区别与联系的探讨，以便对误差与不确定度有更好的理解。
在数据处理方法中，对经常使用的最小二乘法直线拟合进行了不确定度计算的深入探讨，分析了多元线性回归的数据处理方法。
关键词：误差理论；不确定度；最小二乘；线性回归目录引言 (1)第一章、测量与误差 (1)1.1测量与误差的基本概念 (2)1.2随机误差 (2)1.2.1随机误差来源及对测量结果的影响 (2)1.2.2等精度测量 (3)1.2.3不等精度测量 (4)1.3系统误差 (5)1.3.1系统误差来源及对测量结果的影响 (5)1.3.2系统误差的发现 (5)1.4粗大误差 (6)1.4.1粗大误差的产生原因 (6)1.4.2粗大误差的判别方法 (7)第二章、误差的合成与分配 (9)2.1函数误差 (9)2.2随机误差的合成 (10)2.3系统误差的合成 (10)2.4系统误差与随机误差的合成 (11)2.5误差分配 (11)第三章、测量的不确定度评定 (12)3.1测量不确定度 (12)3.1.1不确定度的定义与分类 (12)3.1.2测量不确定度与误差 (13)3.1.3测量不确定度的来源 (13)3.2标准不确定度的评定 (13)3.3测量不确定度的合成 (14)第四章、实验数据处理方法 (14)4.1最小二乘法处理数据 (15)4.2回归分析 (16)4.2.1直线拟合最小二乘法 (16)4.2.2一元线性回归 (18)4.2.3多元线性回归 (19)第五章、结论 (19)引言在自然科学中，人们通过实验得到对事物的认识，实验离不开测量。
本科生实验报告实验课程误差理论与数据处理学院名称核技术与自动化工程学院专业名称辐射防护与核安全学生姓名杨鹏学生学号201306140104指导教师杨强实验地点H2201实验成绩实验一3σ准则与格罗布斯准则的处理应用一、实验目的学会使用EXCEL利用3σ准则与格罗布斯准则对一组数据进行检验与处理。
二、实验内容内容一：表1-1是我国研制国家一级玄武岩标准物质时，参加标准物质含量定值的国内外16个实验室对同一份样品各自给出的Th元素的20个分析结果。
表1-1 国内外19个实验室提供的玄武岩样品中的Th元素含量 (单位：10-6)实验室编号No1 No2 No3 No4 No4 No5 No6 No8 No9 No11分析值，％8.04 7.55 12.6 8.3 8.8 4.99 7.1 8.03 13.8 7.6实验室编号No12 No13 No14 No14 No15 No16 No16 No17 No19 No20分析值，％7.95 56.9 8.1 8.8 7.7 9.37 7.1 8.04 8.11 8.59试对表进行统计计算，利用3σ法和格罗布斯法进行数据处理。
内容二：对文件夹下的实验数据EXCEL进行数据处理分析。
三、实验要求求数据值的均值和标准偏差，绘制数据散点图，利用两种方法剔除离群数据。
四、实验步骤内容一：1）对表1-1数据进行统计计算，并将统计结果记录在表1-2中。
表1-2 数据统计表统计元素 数据个数 平均值 标准差 备注202010.873510.991932）将上述数据按照一倍、两倍、三倍标准偏差进行统计，并画出数据统计分布散点图。
标准偏差 -1 -0.118425876 -0.118425876 121.86542588 21.86543 -2 -11.11035175 -11.1104 232.85735175 32.85735 -3 -22.10227763 -22.1023 343.84927763 43.849283）利用3σ法判断，剔除含有粗大误差的分析数据。
实用文档 标准 《误差理论与数据处理》实验报告 实验名称：MATLAB软件基础 班级：学号： 姓名： 实验时间： 成绩： 一、 实验目的 熟悉MATLAB软件的用户环境；了解MATLAB软件的一般目的命令；掌握MATLAB数组操作与运算函数；掌握MATLAB软件的基本绘图命令；掌握MATLAB语言的几种循环、条件和开关选择结构。
通过该实验的学习，使学生能灵活应用MATLAB软件解决一些简单问题，能借助MATLAB软件进行曲线或图形的绘制。
二、 实验原理 三、 实验内容和结果 1. 程序及流程
1. MATLAB软件的数组操作及运算练习 设有分块矩阵A=[EROS],其中E,R,O,S分别为单位矩阵，随机阵、零阵和对角阵，试通过数值计算验证A2=[ER+RSOS2]
程序： >> E=eye(3); >> R=rand(3,2); >> O=zeros(2,3); >> S=diag([1 2]) >> A=[E R O S] >> a=[E,R+R*S O,S^2] 实用文档 标准 >> A^2-a 2. 直接使用MATLAB软件进行作图练习 1. 在同一个坐标下作出sin(2π*1*t)和cos(2π*10*t)2条曲线的图形，并要求在图上加粗相应标注
程序：>> x=0:0.001:1;
>> plot(x,sin(2*pi*x),x,cos(2*pi*10*x)) 2.用subplot分别在不同的坐标系下作出下列两条曲线，为每幅图形加上标题。
1. 正态分布N(0,1)的概率密度函数曲线； 2. 反正弦分布的概率密度函数曲线，取a=1。 程序：x=-5:0.01:5;
r = randn(1,1); y1=normpdf(x,0,1); y2=1/(pi*sqrt(1-(r ^2))); subplot(2,1,1) plot(x,y1) subplot(2,1,2) plot(x,y2) 3画出下列曲面的3维图形：z=sin（π√x2+y2）。 程序：[x,y]=meshgrid(0:0.25:4*pi);
z=sin(pi*sqrt(x^2+y^2)); mesh(x,y,z); axis([0 4*pi 0 4*pi -2.5 1]); 3. 用MATLAB语言编写命令M-文件和函数M-文件 编写函数M-文件sq.m：用迭代法求x=√a的值。求平方根的迭代公式为xn+1=12（xn+axn）迭代的终止条件为前后两次求出的x的差的绝对值小于10−5。 实用文档 标准 程序：function y=sq(a)
err=10^-5; Xn=a; Xn1=0.5*(Xn+a/Xn) while abs(Xn1-Xn)>= err; Xn=Xn1; Xn1=0.5*(Xn+a/Xn) end y=Xn1;
2. 实验结果（数据或图表） 实用文档
标准 实用文档
标准 3. 结果分析 四、 心得体会 1、通过本次实验，我初步学习使用clc、clear指令，观察command window、command history和workspace等窗口的变化结果。明白了两者的区别：Clc：是清除workspace，command window、command history不变化；Clear 清除workspace，command window、command history不变化。
2、本次实验掌握了一些基本的运算指令，像数组和矩阵的各种运算符号，尤其要注意两者的区别。例如A*B是指内维相同矩阵相乘，而A.*B是指A数组与B数组对应元素的相乘。同时注意矩阵的左乘和右乘。例如A/B是A右除B，指B矩阵乘以A矩阵的逆；而B/A是A左除B，指Ａ矩阵乘以Ｂ矩阵的逆。
3、此外，本实验要掌握一些标准数组生成函数的使用，例如diag（产生对角行矩阵）、eye（产生单位矩阵）等；还有一些数组操作函数，例如det（求方阵的行列式值），rank（求矩阵的秩）。 实用文档
标准 《误差理论与数据处理》实验报告 实验名称：实验数据的统计分析 班级：学号： 姓名： 实验时间： 成绩： 一、 实验目的 通过对试验数据进行统计分析，学习掌握实验数据统计分析的基本方法，学习利用matlab软件编程长生不同分布规律的随机数据并对之进行统计分析，具体包括画出统计直方图，求解均值，方差等统计参数。
二、 实验原理 三、 实验内容和结果 1、 程序及其流程 1. 利用matlab软件编程产生500个均值为10，方差为5的正态分布随机数据，求出该组数据的均值、方差并画出其统计直方图和概率密度曲线
r=10+5.*randn(1,500); bar（r） plot(r) 2. 在同一个坐标下画出正态分布密度N（0,1），N(0,4)和N(10,1)3条曲线的图形，并比较它们之间的差异。
x = [-15:0.001:20]; y1=normpdf(x,0,1);
y2=normpdf(x,0,4); y3=normpdf(x,10,1); plot(x,y1) 实用文档 标准 hold on plot(x,y2) hold on plot(x,y3) 3. 利用matlab软件编程产生500个均匀分布随机数据，求出该组数据的均值、方差并画出其统计直方图和概率密度曲线。
A = unifrnd (0,1,1000,1) bar(A) plot(A) 4. 在同一坐标下滑出标准正态分布，自由度分别为5,10,20的t分布的概率密度曲线，并对之进行比较。
>> bar(A) >> plot(A) >> x=-10:0.01:10; >> y=tpdf(x,5); >> y1=tpdf(x,10); >> y2=tpdf(x,20); >> plot(x,y) >> hold on >> plot(x,y1) >> hold on >> plot(x,y2) >> hold on >> y3=normpdf(x,0,1); >> plot(x,y3) 实用文档 标准 5. 在同一坐标下画出自由度分别为5,10,20的想x^2分布的概率密度曲线，并对之进行比较。
>> x=0:0.01:30; >> y=chi2pdf(x,5); >> y2=chi2pdf(x,10); >> y3=chi2pdf(x,20); >> plot(x,y) >> hold on >> plot(x,y2) >> hold on >> plot(x,y3) 6. 在同一坐标下画出F分布：F(4,5)F(10，20)和F（50,50）的概率密度曲线，并对之进行比较。
>> x=0:0.001:8; >> y=fpdf(x,4,5); >> y2=fpdf(x,10,20); >> y3=fpdf(x,50,50); >> plot(x,y) >> hold on >> plot(x,y2) >> hold on >> plot(x,y3) 2、 实验结果 r = Columns 1 through 1012.6883 19.1694 -1.2942 14.3109 11.5938 3.4616 7.8320 11.7131 27.8920 23.8472 Columns 11 through 203.2506 25.1746 13.6270 9.6847 13.5737 8.9752 9.3793 17.4485 17.0452 17.0860Columns 21 through 30 13.3575 3.9626 13.5862 18.1512 12.4445 15.1735 13.6344 8.4828 11.4694 6.0636 Columns 31 through 4014.4420 4.2646 4.6556 5.9525 -4.7214 17.1919 11.6260 6.2254 16.8515 1.4424 Columns 41 through 50 9.4888 8.7928 11.5960 11.5643 5.6756 9.8497 9.1756 13.1385 15.4663 15.5464 Columns 51 through 605.6817 实用文档 标准 10.3868 3.9294 4.4325 9.9658 17.6632 6.1517 11.8569 8.8721 15.5868 Columns 61 through 704.5547 10.1628 12.7626 15.5031 17.7211 10.4297 2.5420 6.2885 4.6921 21.7523 Columns 71 through 806.9220 13.7404 9.0379 14.4431 6.1758 2.9887 2.8881 12.4410 9.1131 9.0197Columns 81 through 9017.0966 11.4579 10.9891 17.9385 5.9777 13.4831 14.1754 8.7814 11.0784 4.1708Columns 91 through 1004.2602 10.5244 13.6113 22.9275 6.6655 10.9367 9.5875 0.3349 7.8052 1.0266Columns 101 through 11014.2019 5.5598 10.5005 7.2774 11.5176 6.9984 12.4498 13.6968 18.5594 9.0294Columns 111 through 120-0.6918 5.8021 16.7730 4.6392 14.8048 10.6202 17.1835 0.1955 9.0115 3.9608Columns 121 through 13024.5400 14.1261 16.8949 4.7091 7.6569 8.6377 15.4921 8.6106 13.5077 -0.2591Columns 131 through 1408.2308 5.8821 2.1147 12.5399 11.4099 10.1674 3.3316 15.6375 11.7509 8.5047Columns 141 through 15010.1144 8.6900 1.2489 8.5717 5.8432 5.1040 4.2180 7.3322 -0.0132 14.8211Columns 151 through 16012.6003 9.8999 9.8261 6.0092 15.0934 9.3339 6.4273 16.7569 8.8761 7.0549Columns 161 through 1708.5312 5.7604 4.3994 22.6300 18.2775 11.5377 3.7144 5.6727 9.1173 13.9571Columns 171 through 1803.3400 -1.6493 2.7545 11.6676 11.9568 12.2584 9.3486 10.9184 7.6192 14.3101Columns 181 through 1903.1915 12.2751 5.7565 8.3256 12.7639 15.1955 4.4118 16.3033 13.3007 9.6607 Columns 191 through 2009.0239 8.9120 8.4845 10.1152 10.2565 14.1303 17.6349 12.3346 8.9514 13.1260Columns 201 through 21010.9161 4.8512 14.7461 11.5353 10.6759 12.5762 11.3070 5.2926 9.1883 9.2697Columns 211 through 2207.3399 18.4105 5.6214 7.5809 6.4400 4.1289 9.0388 8.6296 17.6504 8.7549Columns 221 through 2304.6789 18.0173 16.1734 8.8519 2.4692 7.7769 9.2203 11.3803 8.6942 12.2171Columns 231 through 24011.9595 3.7466 5.2602 6.2945 7.4609 8.3971 10.0623 -5.1459 7.7149 16.2122Columns 241 through 2504.6665 14.6686 11.7516 9.8550 10.9123 2.1747 9.5773 18.0197 10.4917 10.2069Columns 251 through 2606.3292 9.8459 11.1617 12.1319 8.1360 8.8177 20.1185 -1.2918 21.1472 11.6878Columns 261 through 27015.0003 1.6792 7.0498 8.6097 12.1136 1.6490 12.3582 3.9358 10.3310 13.2618Columns 271 through 28011.6353 15.4132 15.0304 6.7455 11.2853 5.2781 3.3911 14.6241 10.0002 9.7254Columns 281 through 29014.5556 12.9729 11.7510 16.2513 14.6489 11.1988 6.5482 6.7422 15.9605 1.9408 Columns 291 through 3009.8777 0.2558 15.1025 14.3086 10.0058 9.6458 -2.4314 12.9059 -0.9622 -1.5964Columns 301 through 31010.3997 5.2576 12.0575 13.3849 14.2887 6.5442 12.2469 10.5032 14.1303 12.6808Columns 311 through 32014.4894 9.3403 9.2640 15.0389 -0.6183 7.4771 3.6470 8.0871 13.2434 14.1286Columns 321 through 3304.9253 7.6447 10.6851 8.5407 11.5091 11.9997 5.3502 9.1158 -0.6605 15.7268Columns 331 through 3406.8545 3.9808 8.7303 2.8568 9.8957 7.1967 20.8889 15.6923 -2.4844 12.2066Columns 341 through 3503.0093 8.7247 10.8220 13.7387 8.6348 17.8815 7.5953 11.6376 13.3237 10.4259Columns 351 through 36014.4048 11.6161 6.0793 0.9731 19.2930 6.9773 10.5168 12.8158 10.5680 5.476Columns 361 through 3707.6614 9.3756 17.3948 5.6959 13.9233 11.5431 8.8307 4.7151 8.5793 9.5665Columns 371 through 3802.6530 10.9609 5.8885 9.5288 11.6811 5.4767 8.5587 11.7503 0.8207 15.1799Columns 381 through 39022.1223 14.7970 8.4211 12.1431 4.8201 19.3893 14.7035 13.9367 5.6206 11.5997Columns 391 through 4007.2085 8.4429 7.1500 4.8713 5.4563 8.9505 1.5057 13.0380 9.4110 13.4958Columns 401 through 41011.3482 12.4714 2.5844 4.8987 7.7650 10.5483 15.6437 8.5502 16.3078 12.3771Columns 411 through 42015.8706 10.6347 6.7159 2.5930 10.7774 14.0928 8.5371 7.2961 8.4568 4.5170Columns 421 through 4307.5350 9.0963 10.2292 9.6811 13.0567 10.5466 19.0701 11.5601 19.0225 6.3844Columns 431 through 44012.6327 8.6987 13.0007 12.9697 -0.9301 3.3648 2.7949 12.0092 17.3510 8.3659Columns 441 through 45014.0616 12.7277 4.7418 11.9873 6.2405 17.5813 9.8372 18.1800 7.8747 12.9472Columns 451 through 4609.6860 -0.1098 5.0893 13.0626 9.7256 4.4063 6.8681 11.2476 5.0349 14.8748Columns 461 through 4706.7965 19.0443 4.6007 10.9959 2.3949 6.3818 7.0337 12.0067 14.7107 11.5024Columns 471 through 4808.1346 14.0774 13.9944 10.6010 12.8562 12.0640 5.0652 13.7978 6.7140 6.9804Columns 481 through 49010.8847 8.4625 9.3409 12.9768 15.2342 9.0102
