李雅普诺夫稳定性分析

稳态李雅普诺夫稳定性分析在不确定系统控制中的应用研究随着科学技术的快速发展，现代化复杂系统的建模和控制问题变得越来越重要。

不确定性常常是复杂系统中的一个普遍特征，包括参数变化、外部干扰等，而这些因素往往会影响到系统稳定性和性能。

因此，寻找有效的控制方法来保证系统稳定性和性能成为了复杂系统研究中的一个热点问题。

本文将探讨稳态李雅普诺夫稳定性分析在不确定系统控制中的应用研究。

一、稳态李雅普诺夫稳定性分析的基本理论稳态李雅普诺夫稳定性分析是现代系统控制理论中的一个重要分支。

其核心思想是通过研究系统状态变量的稳态变化规律，来判断系统的稳定性特征。

该方法的基本理论可以总结如下：1.1 稳态李雅普诺夫函数稳态李雅普诺夫（LS）函数是指在一定条件下，系统状态变量通过某种方式组合而成的函数。

它可以用来刻画系统在达到稳态时的状态变化规律。

具体而言，稳态LS函数的定义如下：$$V(x)=\int_0^{\infty} \sum_{i=1}^n \frac{\partial V}{\partial x_i}f_i(x,t)p(t)dt$$其中，$x=\left[x_1,x_2,\cdots,x_n\right]^{\mathrm{T}}$是系统状态变量，$f_i(x,t)$是系统状态变量的方程，$p(t)$是某个概率密度函数，$\frac{\partialV}{\partial x_i}$是某个函数。

在该式中，$V(x)$越小，表示稳态时系统的稳定性越强。

1.2 稳态李雅普诺夫函数的性质稳态LS函数具有许多重要的性质，其中最基本的包括：1）非负性：$V(x)\geq0$，且$V(x)=0$当且仅当$x=0$；2）单调性：如果$f_i(x,t)\geq0$，则对于$x_1\neq x_2$，有$V(x_1)-V(x_2)>0$或$V(x_1)=V(x_2)$；3）对称性：如果对于任意的$x$和$y$有$f_i(x,t)=f_i(y,t)$，则$V(x)=V(y)$；4）上界性：如果存在$yu>0$，使得$f_i(x,t)\leq f_i(y,t)$，则有$V(x)\leq V(y)$。

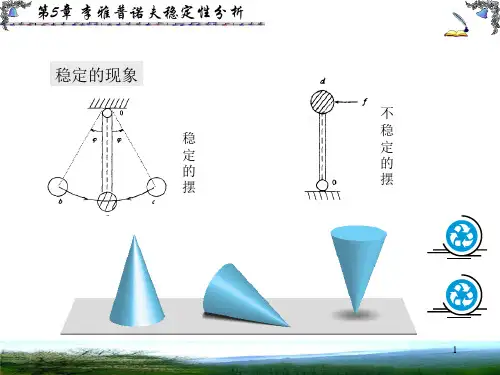
第4章李雅普诺夫稳定性分析李雅普诺夫稳定性分析是数学分析中的一个重要概念，它用于判断非线性系统在其中一点附近的稳定性。

李雅普诺夫稳定性分析方法最初由俄国数学家李雅普诺夫提出，广泛应用于控制论、微分方程和动力系统等领域。

在进行李雅普诺夫稳定性分析时，首先需要确定非线性系统的平衡点。

平衡点是指系统在其中一时刻的状态不再发生变化，即各个状态变量的导数为零。

在平衡点附近，可以通过线性化的方法来近似非线性系统，即将非线性系统转化为线性系统进行分析。

接下来，利用李雅普诺夫稳定性定理可以判断线性化系统的稳定性。

根据定理的不同形式，可以分为不动点稳定性定理和周期解稳定性定理。

不动点稳定性定理是指当线性化系统的特征根都具有负的实部时，非线性系统在平衡点附近是稳定的；而当至少存在一个特征根具有正的实部时，非线性系统在平衡点附近是不稳定的。

这个定理对于线性化系统为一阶系统或者线性化系统的特征根为复数的情况适用。

周期解稳定性定理是指当线性化系统的所有特征根满足一定条件时，非线性系统在周期解附近是稳定的。

这个定理对于封闭曲线解以及周期解的情况适用。

当线性化系统无法满足上述定理时，可以使用李雅普诺夫直接法来判断非线性系统的稳定性。

李雅普诺夫直接法是基于李雅普诺夫函数的概念，通过构造合适的李雅普诺夫函数来判断非线性系统的稳定性。

李雅普诺夫函数是满足以下条件的函数：1）李雅普诺夫函数的导数在其中一区域内是负定的，即导数的每个分量都小于或等于零；2）在平衡点附近，李雅普诺夫函数取得最小值。

通过构造合适的李雅普诺夫函数，并验证满足上述条件，就可以判断非线性系统的稳定性。

如果李雅普诺夫函数的导数在整个状态空间都是负定的，则非线性系统是全局稳定的；如果李雅普诺夫函数的导数在一些有限的状态空间内是负定的，则非线性系统是局部稳定的。

总之，李雅普诺夫稳定性分析是一种有力的工具，可以用于判断非线性系统的稳定性。

不过需要注意的是，李雅普诺夫稳定性分析方法仅适用于平衡点附近的稳定性分析，对于非线性系统的全局稳定性分析还需要其他的方法。

基于MATLAB的李雅普诺夫第二法稳定性分析李雅普诺夫第二法是一种广泛应用于非线性动力系统稳定性分析的方法。

在MATLAB中，我们可以利用多种功能和工具来实现这种分析。

在本文中，将介绍如何使用MATLAB进行李雅普诺夫第二法稳定性分析。

首先，我们将介绍李雅普诺夫第二法的基本概念，然后是在MATLAB中实现该方法的步骤和示例。

李雅普诺夫第二法是一种通过具有特定属性的李雅普诺夫函数来判断非线性系统的稳定性的方法。

具体来说，李雅普诺夫第二法通过找到一个正定函数V(x)以及一个正数a和b，使下式成立：a，x，^2≤V(x)≤b，x，^2其中x是系统状态，x，^2表示欧几里德范数的平方，a和b是正定的。

如果满足这个不等式，那么系统就是稳定的。

现在，我们将介绍在MATLAB中实现李雅普诺夫第二法的步骤。

首先，我们需要编写系统的状态方程。

这可以通过定义一个MATLAB函数来实现。

例如，考虑以下非线性系统：dx/dt = f(x)其中x是系统状态，f(x)是非线性函数。

我们可以将此方程定义为一个名为f.m的函数，它将系统状态作为输入，并返回状态变量的导数。

下面是一个简单的f.m文件的示例：function dxdt = f(x)dxdt = x^2 - x^4;接下来，我们需要选择一个合适的李雅普诺夫函数V(x)。

我们可以通过考虑系统的能量来选择一个合适的函数。

在这种情况下，我们可以选择V(x) = x^2，因为它是系统能量的一种度量方式。

然后，我们需要计算李雅普诺夫函数的时间导数Vdot(x)。

这可以通过将李雅普诺夫函数应用于系统的状态方程来实现。

在MATLAB中，我们可以利用符号计算工具箱来实现这一点。

下面是一个计算Vdot(x)的示例代码：syms xf_sym = x^2 - x^4;V=x^2;Vdot = diff(V, x) * f_sym;最后，我们需要使用MATLAB的求解器来满足条件的李雅普诺夫函数。

理论力学中的稳定性分析有哪些常用方法？在理论力学的领域中，稳定性分析是一个至关重要的课题。

它帮助我们理解和预测物体或系统在各种力的作用下保持平衡或稳定状态的能力。

下面将为您介绍一些常用的稳定性分析方法。

首先，让我们来谈谈静力平衡法。

这是一种基于物体所受的力和力矩来判断稳定性的基本方法。

当一个物体处于静止状态时，如果它所受到的所有外力的合力为零，并且所有外力矩的总和也为零，那么我们就说这个物体处于静力平衡状态。

通过分析这些力和力矩的分布情况，我们可以初步判断物体是否稳定。

例如，一个放置在水平面上的圆柱体，如果它的重心在底面的投影位于底面的范围内，那么它在受到轻微扰动后能够恢复到原来的平衡位置，从而被认为是稳定的；反之，如果重心投影超出底面范围，那么它在受到扰动后就容易倾倒，是不稳定的。

接下来是能量法。

在这种方法中，我们通过分析系统的势能来判断其稳定性。

如果一个系统在平衡位置处的势能具有最小值，那么它在受到微小扰动后，势能会增加，从而产生一个恢复力，使系统回到平衡位置，这表明系统是稳定的。

相反，如果平衡位置处的势能不是最小值，那么系统就是不稳定的。

能量法在处理一些复杂的力学系统时非常有用，尤其是对于那些难以直接通过力和力矩进行分析的情况。

然后是动力法。

这一方法考虑了物体的运动状态和加速度。

通过建立物体的运动方程，并分析其特征值或频率等动态特性，来判断系统的稳定性。

例如，在振动系统中，如果系统的固有频率都是实数且为正值，那么系统是稳定的；如果存在负实部的特征值，那么系统是不稳定的。

李雅普诺夫直接法也是一种重要的稳定性分析方法。

它通过构造一个被称为李雅普诺夫函数的正定函数，来判断系统的稳定性。

如果能够找到这样一个函数，其沿着系统的运动轨迹总是递减的，那么系统就是稳定的。

李雅普诺夫直接法具有广泛的适用性，可以用于线性和非线性系统的稳定性分析。

在实际应用中，还经常会用到数值模拟的方法。

借助计算机软件，如有限元分析（FEA），对物体或系统进行建模，并施加各种力和边界条件，然后通过数值计算来模拟其运动和变形过程，从而判断其稳定性。