常用体积及表面积计算公式
- 格式:doc
- 大小:57.50 KB
- 文档页数:3

一些数学的体积和表面积计算公式3 立方图形名称符号面积S和体积V正方体 a-边长 S=6a2 V=a3长方体 a-长 b-宽 c-高 S=2(ab+ac+bc)V=abc棱柱 S-底面积 h-高 V=Sh棱锥 S-底面积 h-高 V=Sh/3棱台 S1和S2-上、下底面积h-高 V=h[S1+S2+(S1S2)1/2]/3正棱台拟柱体 S1-上底面积 S2-下底面积 S0-中截面积 h-高V=h(S1+S2+4S0)/6圆柱 r-底半径 h-高 C—底面周长 S底—底面积 S侧—侧面积S表—表面积 C=2πr S底=πr2 S侧=Ch S表=Ch+2S底V=S底h=πr2h空心圆柱 R-外圆半径 r-内圆半径 h-高V=πh(R2-r2)直圆锥 r-底半径 h-高V=πr2h/3圆台 r-上底半径 R-下底半径 h-高V=πh(R2+Rr+r2)/3球 r-半径 d-直径V=4/3πr3=πd2/6球缺 h-球缺高 r-球半径 a-球缺底半径V=πh(3a2+h2)/6 =πh2(3r-h)/3a2=h(2r-h)球台 r1和r2-球台上、下底半径 h-高V=πh[3(r12+r22)+h2]/6圆环体 R-环体半径 D-环体直径 r-环体截面半径 d-环体截面直径V=2π2Rr2=π2Dd2/4桶状体 D-桶腹直径 d-桶底直径 h-桶高V=πh(2D2+d2)/12 (母线是圆弧形,圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15 (母线是抛物、、长方形的周长=(长+宽)×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=(上底+下底)×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=(长×宽+长×高+宽×高)×2长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体(正方体、圆柱体)的体积=底面积×高平面图形名称符号周长C和面积S正方形a—边长C=4aS=a2长方形a和b-边长C=2(a+b)S=ab三角形a,b,c-三边长h-a边上的高s-周长的一半A,B,C-内角其中s=(a+b+c)/2 S=ah/2=ab/2·sinC=[s(s-a)(s-b)(s-c)]1/2=a2sinBsinC/(2sinA)四边形d,D-对角线长α-对角线夹角S=dD/2·sinα平行四边形a,b-边长h-a边的高α-两边夹角S=ah=absinα菱形a-边长α-夹角D-长对角线长d-短对角线长S=Dd/2=a2sinα梯形a和b-上、下底长h-高m-中位线长S=(a+b)h/2=mh圆r-半径d-直径C=πd=2πrS=πr2=πd2/4扇形r—扇形半径a—圆心角度数C=2r+2πr×(a/360)S=πr2×(a/360)弓形l-弧长b-弦长h-矢高r-半径α-圆心角的度数S=r2/2·(πα/180-sinα)=r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2 =παr2/360 - b/2·[r2-(b/2)2]1/2=r(l-b)/2 + bh/2≈2bh/3圆环R-外圆半径r-内圆半径D-外圆直径d-内圆直径S=π(R2-r2)=π(D2-d2)/4椭圆D-长轴d-短轴S=πDd/4立方图形名称符号面积S和体积V正方体a-边长S=6a2V=a3长方体a-长b-宽c-高S=2(ab+ac+bc)V=abc棱柱S-底面积h-高V=Sh棱锥S-底面积h-高V=Sh/3棱台S1和S2-上、下底面积h-高V=h[S1+S2+(S1S1)1/2]/3 拟柱体S1-上底面积S2-下底面积S0-中截面积h-高V=h(S1+S2+4S0)/6圆柱r-底半径h-高C—底面周长S底—底面积S侧—侧面积S表—表面积C=2πrS底=πr2S侧=ChS表=Ch+2S底V=S底h=πr2h空心圆柱R-外圆半径r-内圆半径h-高V=πh(R2-r2)直圆锥r-底半径h-高V=πr2h/3圆台r-上底半径R-下底半径h-高V=πh(R2+Rr+r2)/3球r-半径d-直径V=4/3πr3=πd2/6球缺h-球缺高a-球缺底半径V=πh(3a2+h2)/6=πh2(3r-h)/3a2=h(2r-h)球台r1和r2-球台上、下底半径h-高V=πh[3(r12+r22)+h2]/6圆环体R-环体半径D-环体直径r-环体截面半径d-环体截面直径V=2π2Rr2=π2Dd2/4桶状体D-桶腹直径d-桶底直径h-桶高V=πh(2D2+d2)/12(母线是圆弧形,圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15(母线是抛物线形)棱台体体积计算公式:V=(1/3)H(S上+S下+√[S上×S下])H是高,S上和S下分别是上下底面的面积。

1、正方体S=6×a×a;V=a×a×a2,长方体S = 2ab + 2ah + 2bh= 2 ( ab + ah + bh );V = abh3,正四面体当其棱长为a时,其体积等于(√2/12)a^3,表面积等于√3*a^2。
4,圆柱体圆柱的表面积=2×底面积+侧面积;设一个圆柱底面半径为r,高为h,则表面积S:S=2πr^2;+2πrh=2πr(r+h);则体积V:V=πr^2*h5,球体半径是R的球的体积计算公式是:V=(4/3)πR^3(三分之四乘以π乘以R的三次方)。
半径是R的球的表面积计算公式是:S=4πR^2(4倍的π乘以R的二次方)。
6,圆锥的表面积=底面积+侧面积S=πr的平方+πra (注a=母线)圆锥的体积= 1/3πr^2*h7、平面图形周长C和面积S正方形 a—边长 C=4aS=a2长方形 a和b-边长 C=2(a+b)S=ab三角形 a,b,c-三边长h-a边上的高s-周长的一半A,B,C-内角其中s=(a+b+c)/2 S=ah/2 =ab/2·sinC =[s(s-a)(s-b)(s-c)]1/2=a2sinBsinC/(2sinA)四边形 d,D-对角线长α-对角线夹角 S=dD/2·sinα平行四边形 a,b-边长h-a边的高α-两边夹角 S=ah=absinα菱形 a-边长α-夹角D-长对角线长d-短对角线长 S=Dd/2=a2sinα梯形 a和b-上、下底长h-高m-中位线长 S=(a+b)h/2=mh圆 r-半径d-直径 C=πd=2πrS=πr2=πd2/4扇形 r—扇形半径a—圆心角度数C=2r+2πr×(a/360)S=πr2×(a/360)弓形 l-弧长b-弦长h-矢高r-半径α-圆心角的度数 S=r2/2·(πα/180-sinα) =r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2=παr2/360 - b/2·[r2-(b/2)2]1/2=r(l-b)/2 + bh/2≈2bh/3圆环 R-外圆半径r-内圆半径D-外圆直径d-内圆直径 S=π(R2-r2)=π(D2-d2)/4椭圆 D-长轴d-短轴 S=πDd/4立方图形名称符号面积S和体积V正方体 a-边长 S=6a2V=a3长方体 a-长b-宽c-高 S=2(ab+ac+bc)V=abc棱柱 S-底面积h-高 V=Sh棱锥 S-底面积h-高 V=Sh/3棱台 S1和S2-上、下底面积h-高 V=h[S1+S2+(S1S1)1/2]/3 拟柱体 S1-上底面积S2-下底面积S0-中截面积h-高 V=h(S1+S2+4S0)/6圆柱 r-底半径h-高C—底面周长S底—底面积S侧—侧面积S表—表面积 C=2πrS底=πr2S侧=ChS表=Ch+2S底V=S底h=πr2h空心圆柱 R-外圆半径r-内圆半径h-高 V=πh(R2-r2)直圆锥 r-底半径h-高 V=πr2h/3圆台 r-上底半径R-下底半径h-高 V=πh(R2+Rr+r2)/3S=πL(R+r)球 r-半径d-直径 V=4/3πr3=πd2/6球缺 h-球缺高r-球半径a-球缺底半径 V=πh(3a2+h2)/6 面积:S=2πrh =πh2(3r-h)/3a2=h(2r-h)球台 r1和r2-球台上、下底半径h-高 V=πh[3(r12+r22)+h2]/6圆环体 R-环体半径D-环体直径r-环体截面半径d-环体截面直径 V=2π2Rr2=π2Dd2/4桶状体 D-桶腹直径d-桶底直径h-桶高 V=πh(2D2+d2)/12(母线是圆弧形,圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15。

体积和表面积计算公式在数学中,体积和表面积计算是令人头疼的课题。
每个物体的形状及大小都不一样,所以计算它们的体积和表面积时,必须找到正确的公式。
在本文中,将介绍一些体积和表面积计算公式,供大家参考和参考。
首先,介绍一下球体体积和表面积的计算公式。
球体的体积可以用以下公式来计算:V=4/3πr,其中r为球体的半径,π是圆周率。
同时,球体的表面积也可以通过以下公式来计算:S=4πr。
其次,介绍一下圆柱体体积和表面积的计算公式。
由于圆柱体的两端形状是圆形,因此可以借助圆的面积公式来计算它的体积:V=πrh,其中r为圆柱体的半径,h为圆柱体的高度,π是圆周率。
圆柱体的表面积可以用以下公式来计算:S=2πr(r+h)。
此外,介绍一下正方体体积和表面积的计算公式。
由于正方体的四个面是正方形,因此可以用以下公式来计算:V=a,其中a为正方底的边长;正方体的表面积可以用以下公式来计算:S=4a。
再次,介绍一下三棱柱体积和表面积的计算公式。
三棱柱体的体积可以用以下公式来计算:V=αlh,其中α为平面角的余弦值,l为三角柱底面的边长,h为高度;三棱柱体的表面积可以用以下公式来计算:S=l(α+h)。
最后,介绍一下圆锥体体积和表面积的计算公式。
圆锥体的体积可以用以下公式来计算:V=1/3πrh,其中r为圆锥体底部圆的半径,h为圆锥体的高度,π是圆周率;圆锥体的表面积可以用以下公式来计算:S=πrl,其中r为圆锥体底部圆的半径,l为圆锥体侧面的长度。
以上就是本文关于体积和表面积计算公式的详细介绍。
有了以上这些公式,大家就可以轻松的计算出不同物体的体积和表面积了。
只要熟练掌握这些计算公式,就可以很方便的计算出正确的结果。
同时,大家也可以根据自己的需要来灵活运用这些公式,以解决实际的工程计算问题。

立方体的体积和表面积计算立方体是一种常见的几何体,它具有六个相等的正方形面。
在初中数学中,我们经常会遇到计算立方体的体积和表面积的问题。
本文将重点介绍如何计算立方体的体积和表面积,并通过实例进行说明。
一、立方体的体积计算立方体的体积是指立方体所包含的三维空间的大小。
体积的计算公式为:V =边长 ×边长 ×边长,其中V表示体积,边长表示立方体的任意一条边的长度。
例如,如果一个立方体的边长为3厘米,那么它的体积可以通过以下计算得到:V = 3厘米 × 3厘米 × 3厘米 = 27立方厘米。
通过这个简单的例子,我们可以看出,计算立方体的体积只需要将边长相乘即可。
这是因为立方体的六个面都是相等的正方形,所以它的体积就等于边长的立方。
二、立方体的表面积计算立方体的表面积是指立方体所有面的总面积。
计算立方体的表面积需要分别计算六个面的面积,然后将它们相加。
由于立方体的六个面都是正方形,所以每个面的面积可以通过边长的平方来计算。
因此,立方体的表面积计算公式为:S = 6 ×边长×边长,其中S表示表面积。
举个例子,如果一个立方体的边长为4厘米,那么它的表面积可以通过以下计算得到:S = 6 × 4厘米 × 4厘米 = 96平方厘米。
通过这个例子,我们可以看出,计算立方体的表面积只需要将边长的平方乘以6即可。
这是因为立方体的六个面都是相等的正方形,所以它的表面积就等于每个面的面积乘以6。
三、应用举例现在我们通过一些实际问题来应用立方体的体积和表面积的计算。
例题一:一个立方体的体积为64立方米,求它的边长。
解析:根据立方体的体积计算公式,我们可以得到体积为64立方米的立方体的边长为4米。
因为4米 × 4米 × 4米 = 64立方米。
例题二:一个立方体的表面积为54平方厘米,求它的边长。
解析:根据立方体的表面积计算公式,我们可以得到表面积为54平方厘米的立方体的边长为3厘米。

计算多面体的表面积和体积多面体是一个立体几何体,它的表面由多个平面的面构成。
计算多面体的表面积和体积是几何学中的基本问题之一。
本文将介绍如何计算一个多面体的表面积和体积。
一、计算多面体的表面积多面体的表面积是指多面体所有面的总面积。
不同类型的多面体有不同的计算方法,以下分别介绍几种常见多面体的计算方法。
1. 计算正方体的表面积:正方体是一种六个面都是正方形的多面体。
正方体的表面积可以通过以下公式计算:表面积 = 6 × (边长)²2. 计算长方体的表面积:长方体是一种六个面都是矩形的多面体。
长方体的表面积可以通过以下公式计算:表面积 = 2 × (长 ×宽 + 长 ×高 + 宽 ×高)3. 计算球体的表面积:球体是一种所有面都是由半径相等的球面覆盖的多面体。
球体的表面积可以通过以下公式计算:表面积= 4 × π × (半径)²4. 计算圆柱体的表面积:圆柱体是一种由上下底面和侧面围成的多面体。
圆柱体的表面积可以通过以下公式计算:表面积= 2 × π × (半径)² + 2 × π × 半径 ×高5. 计算锥体的表面积:锥体是一种由底面和侧面围成的多面体,其中底面为一个封闭曲面,侧面为多个直线段。
锥体的表面积可以通过以下公式计算:表面积= π × (半径) ×(半径 + 斜高)二、计算多面体的体积多面体的体积是指多面体所包围的空间的大小。
不同类型的多面体有不同的计算方法,以下分别介绍几种常见多面体的计算方法。
1. 计算正方体的体积:正方体的体积可以通过以下公式计算:体积 = (边长)³2. 计算长方体的体积:长方体的体积可以通过以下公式计算:体积 = 长 ×宽 ×高3. 计算球体的体积:球体的体积可以通过以下公式计算:体积= (4/3) × π × (半径)³4. 计算圆柱体的体积:圆柱体的体积可以通过以下公式计算:体积= π × (半径)² ×高5. 计算锥体的体积:锥体的体积可以通过以下公式计算:体积 = (1/3) ×底面积 ×高综上所述,根据不同多面体的类型,我们可以采用相应的公式来计算多面体的表面积和体积。
小学数学常用图形计算公式精读_公式总结如何让小学生学会用数学的思维方式去观察和分析生活,如何帮助他们更好地学好数学这门学科呢?查字典数学网小学频道精心准备了小学数学常用图形计算公式,希望对大家有所帮助!1 、正方形C周长S面积a边长周长=边长×4 C=4a 面积=边长×边长S=a×a2 、正方体V:体积a:棱长表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a3 、长方形C周长S面积a边长周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4 、长方体V:体积s:面积a:长b: 宽h:高(1)表面积(长×宽+长×高+宽×高)×2S=2(ab+ah+bh)(2)体积=长×宽×高V=abh5 三角形s面积a底h高面积=底×高÷2s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6 平行四边形s面积a底h高面积=底×高s=ah7 梯形s面积a上底b下底h高面积=(上底+下底)×高÷2s=(a+b)× h÷28 圆形S面积C周长∏ d=直径r=半径(1)周长=直径×∏=2×∏×半径C=∏d=2∏r(2)面积=半径×半径×∏9 圆柱体v:体积h:高s;底面积r:底面半径c:底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10 圆锥体v:体积h:高s;底面积r:底面半径体积=底面积×高÷3更多小学数学常用图形计算公式和其他相关复习资料,尽在查字典数学网!请大家及时关注!。
体积与表面积的计算知识点总结在数学和物理学中,体积和表面积是基础的计算概念。
体积是指一个物体所占据的空间大小,而表面积则描述了物体外部的相对大小。
这两个概念在科学和实际生活中都具有重要的应用。
本文将总结体积与表面积的计算知识点,以帮助读者更好地理解和运用这些概念。
一、体积的计算体积的计算方法因不同几何体而异。
下面将根据常见几何体的形状介绍其体积的计算方法。
1. 立方体与长方体立方体和长方体是最基本的几何体,它们的体积计算非常简单。
立方体的体积等于边长的立方,公式为V = a³,其中V表示体积,a表示边长。
而长方体的体积则是长度、宽度和高度的乘积,公式为V = l ×w × h,其中l、w和h分别表示长度、宽度和高度。
2. 圆柱体圆柱体的体积计算需要利用底面积和高度。
底面积可通过圆的面积公式计算得出,即A = πr²,其中π为圆周率,r为底面半径。
再将底面积乘以高度h,即可得到圆柱体的体积,公式为V = A × h = πr²h。
3. 圆锥体与圆柱体类似,圆锥体的体积计算也需要利用到底面积和高度。
底面积仍然为A = πr²,而圆锥体的体积等于底面积乘以高度再除以3,公式为V = A × h / 3 = πr²h / 3。
4. 球体球体的体积计算相对复杂一些。
球体的体积等于4/3乘以π与半径r 的立方的乘积,公式为V = (4/3) × πr³。
这个公式是由球的表面积公式导出的。
二、表面积的计算与体积类似,不同几何体的表面积计算方法也不同。
下面将介绍几种常见几何体的表面积计算方法。
1. 立方体与长方体立方体和长方体的表面积计算比较简单,可以根据各个面的尺寸进行求和。
立方体的表面积等于6倍的边长的平方,公式为A = 6a²,其中A表示表面积,a表示边长。
而长方体的表面积等于2倍的长×宽加上2倍的长×高加上2倍的宽×高,公式为A = 2lw + 2lh + 2wh,其中l、w和h分别表示长度、宽度和高度。
长方体表面积和体积计算公式长方体是一种常见的几何体,有着广泛的应用。
在工程、建筑、制造、物流等领域,长方体都扮演着重要的角色。
在计算长方体的体积和表面积时,我们需要使用相应的公式。
1. 长方体的体积公式长方体的体积是指其所占据的空间大小,通常用立方体积单位(如立方米、立方厘米等)来表示。
计算长方体的体积可以使用以下公式:体积 = 长× 宽× 高其中,长、宽、高分别表示长方体的三个相邻的棱长。
例如,一个长方体的长为3厘米、宽为4厘米、高为5厘米,则其体积为3 × 4 × 5 = 60立方厘米。
在实际应用中,我们可以使用尺子、卷尺等工具来测量长方体的三个边长,然后带入公式进行计算,得出长方体的体积。
2. 长方体的表面积公式长方体的表面积是指其六个面积之和,通常用平方面积单位(如平方米、平方厘米等)来表示。
计算长方体的表面积可以使用以下公式:表面积= 2 × (长× 宽 + 长× 高 + 宽× 高)其中,长、宽、高分别表示长方体的三个相邻的棱长。
例如,一个长方体的长为3厘米、宽为4厘米、高为5厘米,则其表面积为2 × (3 × 4 + 3 × 5 + 4 × 5) = 94平方厘米。
在实际应用中,我们可以使用尺子、卷尺等工具来测量长方体的三个边长,然后带入公式进行计算,得出长方体的表面积。
3. 长方体的应用长方体在生活中有着广泛的应用。
例如,我们常见的家具如衣柜、书柜、电视柜、餐桌等都是长方体的形状。
此外,在建筑、制造、物流等领域,长方体也扮演着重要的角色。
例如,在建筑工程中,我们需要计算房间的体积和表面积,以确定所需的建材数量;在制造业中,我们需要计算产品的体积和表面积,以确定所需的原材料数量;在物流行业中,我们需要计算货物的体积和表面积,以确定运输费用。
长方体是一种常见的几何体,其体积和表面积的计算公式十分简单易懂。
二年级科学下长方锥体表面积和体积
长方锥体是一个具有长方形底面和一个顶点的立体图形。
计算长方锥体的表面积和体积是数学中的基本概念。
下面将介绍如何计算长方锥体的表面积和体积。
表面积的计算公式
长方锥体的表面积由底面积和侧面积组成。
计算公式如下:
表面积 = 底面积 + 侧面积
底面积 = 长方形底面的长 ×长方形底面的宽
侧面积 = 底面周长 ×锥体的高 ÷ 2
体积的计算公式
长方锥体的体积是指锥体所包含的三维空间的量。
计算公式如下:
体积 = 底面积 ×锥体的高 ÷ 3
实例计算
假设一个长方锥体的底面长为5cm,底面宽为3cm,锥体的高
为10cm。
那么根据上述公式,我们可以计算出以下结果:
表面积 = 5cm × 3cm + (5cm + 3cm) × 10cm ÷ 2 = 15cm² + 40cm²= 55cm²
体积 = 5cm × 3cm × 10cm ÷ 3 = 50cm³
总结
长方锥体的表面积和体积的计算需要使用相应的公式进行计算。
通过掌握这些计算方法,我们可以更好地理解长方锥体的属性和特点,在科学研究中得到更多的自由探索。
希望本文能帮助您理解和掌握长方锥体的表面积和体积的计算方法。
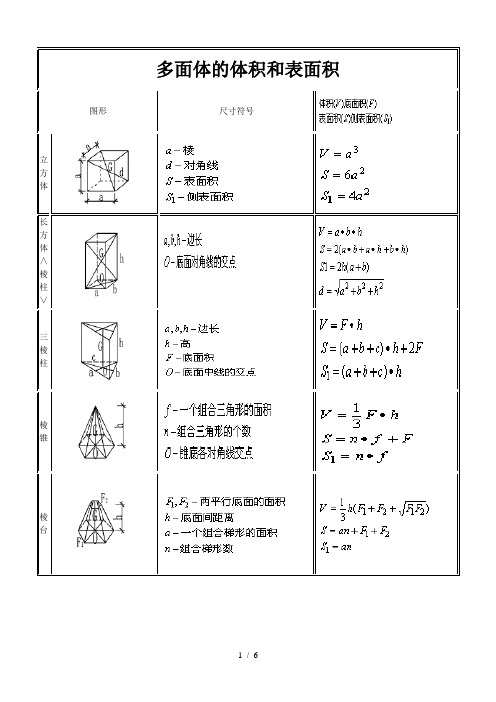
常用体积及表面积计算公式
名称 简 图
计算公式
表面积S、
侧表面积M
体积V
正
立
方
体
26aS 3
aV
长
立
方
体
)(2abbhahS
abhV
圆
柱
dhrhM2
2
hrV
空
心
圆
柱
(
管
)
)(21rrrM
外侧表面
内侧表面积
(2rhV
斜
底
截
圆
柱
)(1hhrM
2
(2hrV
正
六
角
柱
ahaS61962.52 aV5981.2
正
方
角
锥
台
1
22
)(2hbabaS
3
(22baV
球
22
4drS
3
43r
V
圆
锥
22
hrrrlM
3
2
hr
V
截
头
圆
锥
)(1rrlM
3
(212rrhV
r