非稳态传热计算方法及举例

传热学--第三章第三节一维非稳态导热问题§3 — 3 一维非稳态导热的分析解本节介绍第三类边界条件下：无限大平板、无限长圆柱、球的分析解及应用。

如何理解无限大物体，如：当一块平板的长度、宽度>> 厚度时，平板的长度和宽度的边缘向四周的散热对平板内的温度分布影响很少，以至于可以把平板内各点的温度看作仅是厚度的函数时，该平板就是一块“无限大”平板。

若平板的长度、宽度、厚度相差较小，但平板四周绝热良好，则热量交换仅发生在平板两侧面，从传热的角度分析，可简化成一维导热问题。

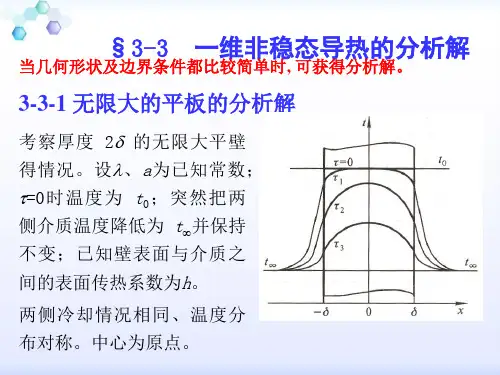
一、无限大平板的分析解已知：厚度的无限大平板，初温t0，初始瞬间将其放于温度为的流体中，而且>t0，流体与板面间的表面传热系数为一常数。

试确定在非稳态过程中板内的温度分布。

解：如图3-5 所示，平板两面对称受热，所以其内温度分布以其中心截面为对称面。

对于x 0 的半块平板，其导热微分方程：(0<x< , )定解条件：t(x,0)= t0(0 x )（边界条件）（边界条件）引入过余温度：则（0<x< , ）(3-9)(x,0)= (0 x ) （初始条件）（边界条件）（边界条件）对偏微分方程分离变量求解得：（3-10 ）其中离散值是下列超越方程的根，称为特征值。

其中Bi 是以特征长度为的毕渥数。

由此可见：平板中的无量纲过余温度与三个无量纲数有关：以平板厚度一半为特征长度的傅立叶数、毕渥数及即：（3-12)二、非稳态导热的正规状况阶段1 、平板中任一点的过余温度与平板中心的过余温度的关系前述得到的分析解是一个无穷级数，计算工作量大，但对比计算表明，当Fo>0.2 时，采用该级数的第一项与采用完整的级数计算平板中心温度的误差小于1% ，因此，当Fo>0.2时，采用以下简化结果：（3-13 ）其中特征值之值与Bi 有关。

由上式（3-13 ）可知：Fo>0.2 以后平板中任一点的过余温度(x ，τ) 与平板中心的过余温度(0 ，τ)=（τ ）之比为：（3-14 ）此式反映了非稳态导热过程中一种很重要的物理现象：即当Fo>0.2 以后，虽然(x ，τ) 与（τ ）各自均与τ 有关，但其比值则与τ 无关，而仅取决于几何位置（x/ ）及边界条件（Bi ）。

第三章 非稳态导热分析解法1、 重点内容：① 非稳态导热的基本概念及特点；② 集总参数法的基本原理及应用；③一维及二维非稳态导热问题。

2、掌握内容：① 确定瞬时温度场的方法；② 确定在一时间间隔内物体所传导热量的计算方法。

3、了解内容：无限大物体非稳态导热的基本特点。

许多工程问题需要确定：物体内部温度场随时间的变化，或确定其内部温度达某一极限值所需的时间。

如：机器启动、变动工况时，急剧的温度变化会使部件因热应力而破坏。

因此，应确定其内部的瞬时温度场。

钢制工件的热处理是一个典型的非稳态导热过程，掌握工件中温度变化的速率是控制工件热处理质量的重要因素；金属在加热炉内加热时，要确定它在炉内停留的时间，以保证达到规定的中心温度。

§3—1 非稳态导热的基本概念一、非稳态导热1、定义：物体的温度随时间而变化的导热过程称非稳态导热。

2、分类：根据物体内温度随时间而变化的特征不同分：1）物体的温度随时间的推移逐渐趋于恒定值，即：const t =↑τ2）物体的温度随时间而作周期性变化1）物体的温度随时间而趋于恒定值如图3-1所示，设一平壁，初值温度t 0，令其左侧的表面温度突然升高到1t 并保持不变，而右侧仍与温度为0t 的空气接触，试分析物体的温度场的变化过程。

首先，物体与高温表面靠近部分的温度很快上升，而其余部分仍保持原来的t 0 。

如图中曲线HBD ，随时间的推移，由于物体导热温度变化波及范围扩大，到某一时间后，右侧表面温度也逐渐升高，如图中曲线HCD 、HE 、HF 。

最后，当时间达到一定值后，温度分布保持恒定，如图中曲线HG （若λ=const ，则HG 是直线）。

由此可见，上述非稳态导热过程中，存在着右侧面参与换热与不参与换热的两个不同阶段。

（1）第一阶段（右侧面不参与换热）温度分布显现出部分为非稳态导热规律控制区和部分为初始温度区的混合分布，即：在此阶段物体温度分布受t 分布的影响较大，此阶段称非正规状况阶段。

1 第三章 非稳态导热的分析计算 3-1 非稳态导热过程分析 一、非稳态导热过程及其特点 导热系统（物体）内温度场随时间变化的导热过程为非稳态导热过程。在过程的进行中系统内各处的温度是随时间变化的，热流量也是变化的。这反映了传热过程中系统内的能量随时间的改变。我们研究非稳态导热过程的意义在于，工程上和自然界存在着大量的非稳态导热过程，如房屋墙壁内的温度变化、炉墙在加热（冷却）过程中的温度变化、物体在炉内的加热或在环境中冷却等。归纳起来，非稳态导热过程可分为两大类型，其一是周期性的非稳态导热过程，其二是非周期性的非稳态导热过程，通常指物体（或系统）的加热或冷却过程。这里主要介绍非周期性的非稳态导热过程。下面以一维非稳态导热为例来分析其过程的主要特征。 今有一无限大平板，突然放入加热炉中加热，平板受炉内烟气环境的加热作用，其温度就会从平板表面向平板中心随时间逐渐升高，其内能也逐渐增加，同时伴随着热流向平板中心的传递。图3-1显示了大平板加热过程的温度变化的情况。 从图中可见，当0时平板处于均匀的温度0tt下,随着时间的增加平板温度开始变化，并向板中心发展，而后中心温度也逐步升高。当时平板温度将与环境温度拉平，非稳态导热过程结束。图中温度分布曲线是用相同的来描绘的。总之，在非稳态导热过程中物体内的温度和热流都是在不断的变化，而且都是一个不断地从非稳态到稳态的导热过程，也是一个能量从不平衡到平衡的过程。 二、加热或冷却过程的两个重要阶段

从图3-1中也可以看出，在平板加热过程的初期，初始温度分布0tt仍然在影响物体整个的温度分布。只有物体中心的温度开始变化之后(如图中τ>τ2之后)，初始温度分布0tt的影响才会消失，其后的温度分布就是一条光滑连续的曲线。据此，我们可以把非稳态导热过程分为两个不同的阶段，即： 初始状况阶段――环境的热影响不断向物体内部扩展的过程，也就是物体（或系统）仍然有部分区域受初始温度分布控制的阶段； 正规状况阶段――环境对物体的热影响已经扩展到整个物体内部，且仍然继续作用于物体的过程，也就是物体（或系统）的温度分布不再受初始温度分布影响的阶段。 由于初始状况阶段存在初始温度分布的影响而使物体内的整体温度分布必须用无穷级数来加以描述，而在正规状况阶段，由于初始温度影响的消失，温度分布曲线变为光滑连续的曲线，因而可以用初等函数加以描述，此时只要无穷级数的首项来表示物体内的温度分布。 3 边界条件对导热系统温度分布的影响 从上面的分析不难看出，环境（边界条件）对系统温度分布的影响是很显著的，且在整个过程中都一直在起作用。因此，分析一下非稳态导热过程的边界条件是十分重要的，