河北专版九年级数学下册专项训练九实践操作图形的剪切、拼接、折叠等新版
- 格式:ppt
- 大小:15.13 MB
- 文档页数:11


第二十八章 锐角三角函数 28.1 锐角三角函数第1课时 正弦基础题知识点1 已知直角三角形的边长,求锐角的正弦值1.如图,在Rt △ABC 中,∠C =90°.若AB =5,BC =3,则sinA =(A)A.35B.45C.34D.432.(2018·孝感)如图,在Rt △ABC 中,∠C =90°,AB =10,AC =8,则sinA 等于(A)A.35B.45C.34D.433.(教材P65练习T2变式)将Rt △ABC 三边的长度都扩大为原来的3倍,则锐角A 的正弦值(A)A .不变B .缩小为原来的13C .扩大为原来的3倍D .不能确定4.如图,P 是∠α的边OA 上一点,点P 的坐标为(12,5),则∠α的正弦值为513. 5.分别求出图1,图2中∠A ,∠B 的正弦值.图1 图2解:图1中AC =AB 2-BC 2=62-22=42, ∴sinA =BC AB =26=13,sinB =AC AB =426=223.图2中AB =AC 2+BC 2=(6)2+(2)2=22, ∴sinA =BC AB =222=12,sinB =AC AB =622=32.6.(教材P64练习T1变式)如图所示,在Rt △ABC 中,∠C =90°,a ∶c =2∶3,求sinA 和sinB 的值.解:在Rt △ABC 中,∠C =90°,a ∶c =2∶3, 设a =2k ,c =3k(k>0), ∴b =c 2-a 2=5k.∴sinA =a c =2k 3k =23,sinB =b c =5k 3k =53.知识点2 已知锐角的正弦值,求直角三角形的边长 7.在Rt △ABC 中,∠C =90°,sinA =35,BC =6,则AB =(D)A .4B .6C .8D .108.在△ABC 中,AB =AC =5,sin ∠ABC =0.8,则BC =6.9.如图,在△ABC 中,∠C =90°,sinA =45,AB =15,求△ABC 的周长.解:在Rt △ABC 中,∠C =90°, AB =15,sinA =BC AB =45,∴BC =12,AC =AB 2-BC 2=152-122=9. ∴△ABC 的周长为9+12+15=36. 易错点 点的位置不确定10.(分类讨论思想)已知正方形ABCD 的边长为2,点P 是直线CD 上一点.若DP =1,则sin ∠BPC 5或13中档题11.如图,在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD =2,AC =3,则sinB 的值为(C)A.23B.43C.34D.3512.如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D.若AC =5,BC =2,则sin ∠ACD 的值为(A)A.53B.255C.52D.2313.如图所示,△ABC 的顶点是正方形网格的格点,则sinC 的值为(B)A.23B.21313C.31313D.131314.如图,⊙O 的直径CD =10 cm ,且AB ⊥CD ,垂足为P ,AB =8 cm ,则sin ∠OAP =35.15.如图,已知直线l 1∥l 2∥l 3∥l 4,相邻两条平行直线间的距离都是1.如果正方形ABCD 的四个顶点分别在四条直线上,那么sin α516.如图,菱形ABCD 的边长为10 cm ,DE ⊥AB ,sinA =35,求DE 的长和菱形ABCD 的面积.解:∵DE ⊥AB , ∴∠AED =90°.在Rt △AED 中,sinA =DE AD ,即35=DE10.解得DE =6.∴菱形ABCD 的面积为10×6=60(cm 2).17.如图,已知⊙O 的半径为5 cm ,弦AB 的长为8 cm ,P 是AB 延长线上一点,BP =2 cm ,求sin ∠OPA 的值.解:作OC ⊥AB 于点C. 根据垂径定理,得 AC =BC =4.(cm)∴CP =4+2=6(cm).在Rt △OAC 中,根据勾股定理,得 OC =OA 2-AC 2=52-42=3(cm). 在Rt △OCP 中,根据勾股定理,得 OP =OC 2+CP 2=32+62=35(cm). 故sin ∠OPA =OC OP =335=55.综合题18.如图,在矩形ABCD 中,AB =8,BC =12,点E 是BC 的中点,连接AE ,将△ABE 沿AE 折叠,点B 落在点F 处,连接FC ,则sin ∠ECF =(D)A.34 B.43C.35D.45第2课时 锐角三角函数基础题知识点1 余弦1.(2017·湖州)如图,已知在Rt △ABC 中,∠C =90°,AB =5,BC =3,则cosB 的值是(A)A.35B.45C.34D.432.如图,在Rt △ABC 中,∠C =90°,AB =6,cosB =23,则BC 的长为(A)A .4B .2 5C.181313D.1213133.如图,在平面直角坐标系中,点A 的坐标为(4,3),那么cos α的值是(D)A.34B.43C.35D.454.如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8,则AB =10,cosA =35.知识点2 正切5.在Rt △ABC 中,∠C =90°,tanB =32,BC =23,则AC 等于(C) A .4 5B .4C .3D .66.(2018·广州)如图,旗杆高AB =8 m ,某一时刻,旗杆影子长BC =16 m ,则tanC =12.7.已知等腰三角形的腰长为6 cm ,底边长为10 cm 58.如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D.若BC =2,AB =3,求tan ∠BCD 的值.解:∵CD ⊥AB ,∴∠ADC =90°. ∴∠A +∠ACD =90°.又∵∠BCD +∠ACD =∠ACB =90°, ∴∠BCD =∠A.在Rt △ABC 中,AC =AB 2-BC 2=32-22= 5. ∴tanA =BC AC =25=255.∴tan ∠BCD =tanA =255.知识点3 锐角三角函数9.(2017·宜昌)△ABC 在网格中的位置如图所示(每个小正方形的边长为1),AD ⊥BC 于点D ,下列四个选项中,错误的是(C)A .sin α=cos αB .tanC =2C .sin β=cos βD .tan α=110.(2018·滨州)在△ABC 中,∠C =90°.若tanA =12,则sinB 511.在Rt △ABC 中,∠C =90°,AC =7,BC =24.(1)求AB 的长;(2)求sinA ,cosA ,tanA 的值. 解:(1)由勾股定理,得AB =AC 2+BC 2=72+242=25.(2)sinA =BC AB =2425,cosA =AC AB =725,tanA =BC AC =247.中档题12.在Rt △ABC 中,∠C =90°,若斜边AB 是直角边BC 的3倍,则tanB 的值是(D)A.13B .3C.24D .2 213.(2018·河北考试说明)如图,梯子(长度不变)跟地面所成的锐角为∠A ,关于∠A 的锐角三角函数值与梯子的倾斜程度之间,叙述正确的是(A)A .sinA 的值越大,梯子越陡B .cosA 的值越大,梯子越陡C .tanA 的值越小,梯子越陡D .陡缓程度与∠A 的锐角三角函数值无关14.如图,以O 为圆心,1为半径的弧交坐标轴于A ,B 两点,P 是弧上一点(不与A ,B 重合),连接OP ,设∠POB =α,则点P 的坐标是(C)A .(sin α,sin α)B .(cos α,cos α)C .(cos α,sin α)D .(sin α,cos α)15.已知抛物线y =-x 2-2x +3与x 轴交于A ,B 两点,将这条抛物线的顶点记为C ,连接AC ,BC ,则tan ∠CAB 的值为(D)A. 3B.55C.255D .216.(转化思想)(2018·河北考试说明)如图,∠1的正切值等于13.17.如图,在△ABC 中,AB =AC ,∠A =45°,AC 的垂直平分线分别交AB ,AC 于D ,E 两点,连接CD.如果AD =1,那么tan ∠BCD18.如图,在△ABC 中,CD ⊥AB ,垂足为D.若AB =12,CD =6,tanA =32,求sinB +cosB 的值.解:在Rt △ACD 中, CD =6,tanA =32,∴CD AD =6AD =32, 即AD =4.又∵AB =12,∴BD =AB -AD =8. 在Rt △BCD 中,BC =CD 2+BD 2=10.∴sinB =CD BC =610=35,cosB =BD BC =810=45.∴sinB +cosB =35+45=75.综合题19.(2018·荆州)如图,在平面直角坐标系中,⊙P 经过三点A(8,0),O(0,0),B(0,6),点D 是⊙P 上的一动点.当点D 到弦OB 的距离最大时,tan ∠BOD 的值是(B)A .2B .3C .4D .520.如图,将矩形ABCD 沿CE 折叠,点B 恰好落在边AD 的F 处.如果AB BC =23,那么tan ∠DCF 2提示:∵四边形ABCD 是矩形, ∴AB =CD ,∠D =90°. ∵AB BC =23,且由折叠知,CF =BC ,∴CD CF =23. 设CD =2x ,CF =3x(x>0), ∴DF =CF 2-CD 2=5x. ∴tan ∠DCF =DF CD =5x 2x =52.21.如图所示,正方形ABCD 边长为2,点E 在CB 的延长线上,BD =BE ,则tan ∠BAE 的值为(C)A.22B .1C. 2D .2 2第3课时 特殊角的锐角三角函数值基础题知识点1 特殊角的锐角三角函数值 1.tan60°的值等于(D)A.12B.33C.32D. 3 2.(2018·河北第二次模拟大联考)cos30°的相反数是(C)A .-12B .-33C .-32D .-223.(2018·白银)计算:2sin30°+(-1)2 018-(12)-1=0. 4.计算:tan45°+2cos45°=2.5.在等腰△ABC 中,∠C =90°,则tanA =1. 6.(教材P67练习T1变式)计算:(1)sin30°+cos45°;解:原式=12+22=1+22.(2)cos30°·tan30°-tan45°; 解:原式=32×33-1=12-1=-12.(3)sin 260°+cos 260°;解:原式=(32)2+(12)2=1.(4)22sin45°+sin60°·cos45°. 解:原式=22×22+32×22=2+64.知识点2 由锐角三角函数值求特殊角7.(2018·河北考试说明)在Rt △ABC 中,∠C =90°,如果cosB =12,那么sinA 的值是(B)A .1B.12C.32D.228.(2018·河北模拟)在△ABC 中,若|cosA -32|+(1-tanB)2=0,则∠C 的度数是(D) A .45°B .60°C .75°D .105°9.如果在△ABC 中,sinA =cosB =22,那么下列最确切的结论是(C) A .△ABC 是直角三角形 B .△ABC 是等腰三角形 C .△ABC 是等腰直角三角形 D .△ABC 是锐角三角形知识点3 用计算器计算锐角三角函数值10.如图是我们数学课本上采用的科学计算器面板,利用该型号计算器计算2cos55°,按键顺序正确的是(C)11.已知sinA =0.370 6,则锐角A =21.75°.(保留两位小数)12.利用计算器求∠A =18°36′的三个锐角三角函数值.(结果保留四位小数)解:sinA =sin18°36′≈0.319 0, cosA =cos18°36′≈0.947 8, tanA =tan18°36′≈0.336 5.中档题13.如图,以O 为圆心,任意长为半径画弧,与射线OM 交于点A ,再以A 为圆心,AO 长为半径画弧,两弧交于点B ,画射线OB ,则sin ∠AOB 的值等于(C)A.12B.22C.32D. 314.菱形OABC 在平面直角坐标系中的位置如图所示,∠AOC =45°,OC =2,则点B 的坐标为(C)A .(2,1)B .(1,2)C .(2+1,1)D .(1,2+1)15.如图,点O 在△ABC 内,且到三边的距离相等.若∠BOC =120°,则tanA 的值为(A)A. 3B.33C.32D.2216.式子2cos30°-tan45°-(1-tan60°)2的值是0.17.(2017·烟台)在Rt △ABC 中,∠C =90°,AB =2,BC =3,则sin A 2=12.18.正比例函数y =33x 的图像与x 轴的夹角为α,则α=30°. 19.计算:(1)8×sin45°-2 0180+2-1; 解:原式=22×22-1+12=2-1+12=32.(2)|-3|+2sin45°+tan60°-(-13)-1-12+(π-3)0.解:原式=3+2×22+3-(-3)-23+1 =3+1+3+3-23+1 =5.20.已知α为锐角,且tan α是方程x 2+2x -3=0的一个根,求2sin 2α+cos 2α-3tan(α+15°)的值.解:解方程x 2+2x -3=0,得x 1=1,x 2=-3. ∵tan α>0,∴tan α=1.∴α=45°.∴2sin 2α+cos 2α-3tan(α+15°)=2sin 245°+cos 245°-3tan(45°+15°)=2sin 245°+cos 245°-3tan60° =2×(22)2+(22)2-3× 3 =-32.综合题21.如图,在Rt △BCD 中,∠BDC =30°,延长CD 到点A ,连接AB ,∠A =15°,求tan 15°的值.(结果保留根号,提示:12+3=2-3(2+3)(2-3)=2-3)解:∵∠A =15°,∠BDC =30°, ∴∠ABD =∠BDC -∠A =15°. ∴AD =BD.设BC =x ,在Rt △BDC 中,∵∠BDC =30°, ∴BD =2BC =2x ,DC =BD 2-BC 2=3x. ∴AD =BD =2x ,AC =AD +DC =(2+3)x.在Rt △ABC 中,tan15°=BC AC =x(2+3)x=2- 3.22.如图为张小亮的答卷,他的得分应是(C)姓名__张小亮__ 得分 __?__填空(每小题20分,共100分)①sin30°=12.②tan30°-13-1.③若∠α的补角为135°,则cos α2④若钝角α满足3tan(α+20°)=1,则∠α=30°. ⑤在sin60°,3.14,π,0中,无理数的个数为2.A .100分B .80分C .60分D .40分河北常考点专题(六) 求锐角三角函数值的常用方法方法1 定义法直接根据定义求三角函数值,首先求出相应边的长度,然后代入三角函数公式计算即可.1.如图,在△ABC 中,DE 是BC 的垂直平分线,DE 交AC 于点E ,连接BE.若BE =5,BC =6,则cosC =35.2.如图,PA 与⊙O 相切于点A ,PC 经过圆心且与该圆相交于点B ,C 两点.若PA =4,PB =2,则sinP =35.方法2 设参数法若已知两边的比值或一个三角函数值,而不能直接求出三角函数相应边的长,则可采用设参数的方法,先用参数表示出三角函数相应边的长,再根据三角函数公式计算它们的比值,即可得出三角函数值.3.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D.若BD∶CD=3∶2,则tanB=(D)A.32B.23C.62D.634.(2018·枣庄)如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是 (A)A.24B.14C.13D.235.(2018·泰安)如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A′处.若EA′的延长线恰好过点C,则sin∠ABE106.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).(1)求证:△ACE≌△AFE;(2)求tan∠CAE的值.解:(1)证明:∵AE是∠BAC的平分线,EC⊥AC,EF⊥AF,∴CE=FE.在Rt△ACE和Rt△AFE中,⎩⎪⎨⎪⎧CE =FE ,AE =AE ,∴Rt △ACE ≌Rt △AFE(HL). (2)由(1)可知△ACE ≌△AFE , ∴AC =AF.设BF =m ,则AC =AF =2m ,∴AB =3m. ∴BC =AB 2-AC 2=9m 2-4m 2=5m.∴在Rt △ABC 中,tanB =AC BC =2m 5m =25.在Rt △EFB 中,EF =BF ·tanB =2m 5,∴CE =EF =2m 5.在Rt △ACE 中,tan ∠CAE =CE AC =2m52m =55,∴tan ∠CAE =55.方法3 等角转换法若要求的角的三角函数值不容易求出,且这个角可以转化为其他角,则可以直接求转化后的角的三角函数值.7.如图,A ,B ,C 三点在正方形网格线的交点处.若将△ABC 绕着点A 逆时针旋转得到△AB ′C ′,则tanB ′的值为(B)A.12B.13C.14D.248.如图,点D(0,3),O(0,0),C(4,0)在⊙A 上,BD 是⊙A 的一条弦,则sin ∠OBD =(D)A.12B.34C.45D.359.(2018·河北模拟)将一张矩形纸片ABCD 如图那样折起,使顶点C 落在C ′处,测量得AB =4,DE =8.则sin ∠C ′ED 的值为(B)A .2B.12C.22D.3210.如图,在Rt △ABC 中,∠ACB =90°,AC =8,BC =6,CD ⊥AB ,垂足为D ,则tan ∠BCD 的值是34.11.如图,点E 在正方形ABCD 的边AB 上,连接DE ,过点C 作CF ⊥DE 于点F ,过点A 作AG ∥CF 交DE 于点G.(1)求证:△DCF ≌△ADG ;(2)若点E 是AB 的中点,设∠DCF =α,求sin α的值.解:(1)证明:在正方形ABCD 中,AD =DC ,∠ADC =90°, ∵CF ⊥DE ,∴∠CFD =∠CFG =90°. ∵AG ∥CF ,∴∠AGD =∠CFG =90°. ∴∠AGD =∠CFD.又∵∠ADG +∠CDE =∠ADC =90°, ∠DCF +∠CDE =90°, ∴∠ADG =∠DCF. 在△DCF 和△ADG 中, ⎩⎪⎨⎪⎧∠DFC =∠AGD ,∠DCF =∠ADG ,DC =AD ,∴△DCF ≌△ADG(AAS).(2)设正方形ABCD 的边长为2a. ∵点E 是AB 的中点, ∴AE =12×2a =a.在Rt △ADE 中,DE =AD 2+AE 2=(2a )2+a 2=5a , ∴sin ∠ADG =AE DE =a 5a =55.∵∠ADG =∠DCF =α, ∴sin α=55. 方法4 构造直角三角形若要求三角函数值的角不在直角三角形中,则需要我们根据已知条件构造直角三角形解决.12.在平面直角坐标系中,已知点A(2,1)和点B(3,0),则sin ∠AOB 的值等于(A)A.55 B.52 C.32 D.1213.(2018·河北沧州期末)如图所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为(C)A.102B.32C.55D.2314.(2017·贵港)如图,点P 在等边△ABC 的内部,且PC =6,PA =8,PB =10,将线段PC 绕点C 顺时针旋转60°得到P ′C ,连接AP ′,则sin ∠PAP ′的值为35.28.2 解直角三角形及其应用28.2.1 解直角三角形基础题知识点1 已知两边解直角三角形1.在△ABC 中,∠C =90°,AC =3,AB =4,欲求∠A 的值,最适宜的做法是(C)A .计算tanA 的值求出B .计算sinA 的值求出C .计算cosA 的值求出D .先根据sinB 求出∠B ,再利用90°-∠B 求出2.(2017·日照)在Rt △ABC 中,∠C =90°,AB =13,AC =5,则sinA 的值为(B)A.513B.1213C.512D.1253.在Rt △ABC 中,∠C =90°,a =20,c =202,则∠A =45°,∠B b4.(教材P73例1变式)如图,在Rt △ABC 中,∠C =90°,已知BC ==解:∵tanA =BC AC =2662=33,∴∠A =30°.∴∠B =90°-∠A =90°-30°=60°, AB =2BC =4 6.知识点2 已知一边和一锐角(或锐角的三角函数值)解直角三角形5.如图,在△ABC 中,∠C =90°,∠B =50°,AB =10,则BC 的长为(B)A .10tan50°B .10cos50°C .10sin50°D.10cos50°6.如果等腰三角形的底角为30°,腰长为6 cm ,那么这个三角形的面积为(B) A .4.5 cm 2B .9 3 cm2C .18 3 cm 2D .36 cm 27.(2017·广州)如图,在Rt △ABC 中,∠C =90°,BC =15,tanA =158,则AB =17.8.(教材P73例2变式)在Rt △ABC 中,∠C =90°,c =83,∠A =60°,解这个直角三角形. 解:∵∠A =60°,∴∠B =90°-∠A =30°.∴b =12c =4 3.∵sinA =ac,∴a =c ·sinA =83×sin60°=83×32=12. 9.如图,在Rt △ABC 中,∠C =90°,∠B =55°,AC =4,解此直角三角形.(结果保留小数点后一位)解:∵∠B =55°,∠A =90°-∠B =90°-55°=35°. ∵tanB =ACBC ,∴BC =AC tanB =4tan55°≈2.8. ∵sinB =ACAB ,∴AB =AC sinB =4sin55°≈4.9. 易错点 忽视钝角三角形而漏解10.(分类讨论思想)在△ABC 中,AB =23,AC =2,∠B =30°,则∠C =60°或120°,BC =2或4.中档题11.如图,⊙O 是正五边形ABCDE 的外接圆,这个正五边形的边长为a ,半径为R ,边心距为r ,则下列关系式错误的是(A)A .R 2-r 2=a 2B .a =2Rsin36°C .a =2rtan36°D .r =Rcos36°12.在△ABC 中,AB =122,AC =13,cosB =22,则BC 边的长为(D) A .7 B .8C .8或17D .7或1713.(2018·河北考试说明)如图,在▱ABCD 中,AB =8,AD =5,sinA =45,E 是DC 上一点,且BE =BC ,则DE 的长为2.14.如图,在四边形ABCD 中,对角线AC ,BD 相交于点E ,∠DAB =∠CDB =90°,∠ABD =45°,∠DCA =30°,AB =6,则AE =2.15.(2018·河北考试说明)如图,在Rt △ABC 中,∠C =90°,BC =8,tanB =12,点D 在BC 上,且BD =AD.求AC的长和cos ∠ADC 的值.解:∵在Rt △ABC 中,BC =8,tanB =12,∴AC =4.设AD =x ,则BD =x ,CD =8-x ,由勾股定理,得(8-x)2+42=x 2.解得x =5. ∴cos ∠ADC =DC AD =35.16.已知:如图,在△ABC 中,AB =AC =9,BC =6.求:(1)sinC 的值;(2)AC 边上的高BD 的长.解:(1)作AE ⊥BC 交BC 于点E. ∵AB =AC ,∴BE =EC =3. 在Rt △AEC 中,AE =92-32=62,∴sinC =AE AC =629=223.(2)在Rt △BDC 中,sinC =BDBC ,∴BD 6=223.∴BD =4 2. 综合题17.探究:已知,如图1,在△ABC 中,∠A =α(0°<α<90°),AB =c ,AC =b ,试用含b ,c ,α的式子表示△ABC 的面积;图1 图2应用:如图2,在▱ABCD 中,对角线AC ,BD 相交成的锐角为α,若AC =a ,BD =b ,试用含b ,c ,α的式子表示▱ABCD 的面积.解:探究:过点B 作BD ⊥AC ,垂足为D. ∵AB =c ,∠A =α,∴BD =c ·sin α.∴S △ABC =12AC ·BD =12bcsin α.应用:过点C 作CE ⊥DO 于点E. ∴sin α=ECCO.∵在▱ABCD 中,AC =a ,BD =b , ∴CO =12a ,DO =12b.∴S △BCD =12CE ·BD=12×12asin α×b =14absin α. ∴S ▱ABCD =2S △BCD =12absin α.河北必考点专题(七) 与解直角三角形有关的综合类型1 三角形、四边形中的三角函数1.如图所示,在矩形ABCD 中,DE ⊥AC 于点E ,设∠ADE =α,且cos α=35,AB =4,则AD 的长为(B)A .3B.163C.203D.1652.(2018·湖州)如图,已知菱形ABCD ,对角线AC ,BD 相交于点O.若tan ∠BAC =13,AC =6,则BD 的长是2.3.如图,在四边形ABCD 中,∠B =∠D =90°,AB =3,BC =2,tanA =43,则CD =65.4.(2017·石家庄模拟)如图,在矩形ABCD 中,BC =2,将矩形ABCD 绕点D 顺时针旋转90°,点A ,C 分别落在点A ′,C ′处,并且点A ′,C ′,B 在同一条直线上,则tan ∠ABA 25.如图,在正方形ABCD 中,DE ⊥AM 于点E ,BF ⊥AM 于点F.若AF =2,四边形ABED 的面积为24,则sin ∠EBF 136.如图,在矩形ABCD 中,AB =4,BC =6,点E 为BC 的中点,连接AE ,将△ABE 沿AE 折叠,点B 落在点B ′处,则sin ∠B ′EC 的值为2425.7.(2018·石家庄新华区二模)如图是由六个全等的菱形组成的网格图,菱形的顶点称为格点,A ,O ,B ,C 均在格点上.当菱形的边长为1且∠AOB =60°时,则有AB sin ∠ABC 148.(2018·邢台宁晋县模拟)已知:如图,在△ABC 中,∠ACB =90°,CD ⊥AB 于点D ,BE ∶AB =3∶5.若CE =2,cos ∠ACD =45.求:(1)cos ∠ABC 的值; (2)AC 的长.解:(1)在Rt △ACD 与Rt △ABC 中,∵∠ABC +∠CAD =90°,∠ACD +∠CAD =90°, ∴∠ABC =∠ACD.∴cos ∠ABC =cos ∠ACD =45.(2)在Rt △ABC 中,cos ∠ABC =BC AB =45,令BC =4k ,AB =5k ,则AC =3k.由BE ∶AB =3∶5, 知BE =3k.则CE =k.∵CE =2, ∴k =2,AC =3 2.9.(分类讨论思想)(2017·河北改编)平面内,如图,在▱ABCD 中,AB =10,AD =15,tanA =43,点P 为AD 边上任意一点,连接PB ,将PB 绕点P 逆时针旋转90°得到线段PQ.(1)当∠DPQ =10°时,求∠APB 的大小;(2)当tan ∠ABP ∶tanA =3∶2时,求点Q 与点B 间的距离(结果保留根号). 解:(1)如图1,①当点Q 在▱ABCD 内时,∠AP ′B =180°-∠Q ′P ′B -∠Q ′P ′D =180°-90°-10°=80°. ②当点Q 在▱ABCD 外时,∠APB =180°-(∠QPB -∠QPD)=180°-(90°-10°)=100°. 综上所述,当∠DPQ =10°时,∠APB 为80°或100°.图1图2(2)如图2,连接BQ ,作PE ⊥AB 于点E.∵tan ∠ABP ∶tanA =3∶2,tanA =43,∴tan ∠ABP =2.在Rt △APE 中,tanA =PE AE =43,设PE =4k ,则AE =3k.在Rt △PBE 中,tan ∠ABP =PEEB =2,∴EB =2k. ∴AB =5k =10. ∴k =2.∴PE =8,EB =4.∴PB =82+42=4 5.∵△BPQ 是等腰直角三角形,∴BQ =2PB =410. 类型2 圆中的三角函数10.如图,AB 是⊙O 的直径,C 是⊙O 上的点,过点C 作⊙O 的切线交AB 的延长线于点E.若∠A =30°,则sinE 的值为(A)A.12B.22C.32D.3311.如图,已知△ABC 的外接圆O 的半径为3,AC =4,则sinB 的值为23.12.(分类讨论思想)(2018·石家庄裕华区一模)如图1、图2,在圆O 中,OA =1,AB =3,将弦AB 与弧AB 所围成的弓形(包括边界的阴影部分)绕点B 顺时针旋转α度(0≤α≤360),点A 的对应点是A ′.(1)点O 到线段AB 的距离是12;∠AOB =120°;点O 落在阴影部分(包括边界)时,α的取值范围是30°≤α≤60°;(2)如图3,线段A ′B 与优弧ACB 的交点是D ,当∠A ′BA =90°时,说明点D 在AO 的延长线上; (3)当直线A ′B 与圆O 相切时,求α的值并求此时点A ′运动路径的长度.解:(2)连接AD ,∵∠A ′BA =90°, ∴AD 为直径.∴D 在AO 的延长线上.(3)①当A ′B 与⊙O 相切,∴∠OBA ′=90°.此时∠ABA ′=90°+30°=120° 或∠ABA ′=90°-30°=60° ∴α=120°或300°. ②当α=120°时,A ′运动路径的长度=120·3180=233π.当α=300°时,A ′运动路径的长度=300π·3180=533π.13.(分类讨论思想)(2018·河北)如图,点A 在数轴上对应的数为26,以原点O 为圆心,OA 为半径作优弧AB ︵,使点B 在O 右下方,且tan ∠AOB =43,在优弧AB ︵上任取一点P ,且能过P 作直线l ∥OB 交数轴于点Q.设Q 在数轴上对应的数为x ,连接OP.(1)若优弧AB ︵上一段AP ︵的长为13π,求∠AOP 的度数及x 的值; (2)求x 的最小值,并指出此时直线l 与AB ︵所在圆的位置关系; (3)若线段PQ 的长为12.5,直接写出这时x 的值.解:(1)由题意知,r =OA =26,AP ︵的长为=13π, ∴n πr 180=n π×26180=13π, ∴n =90°.∴∠AOP =90°. ∵l ∥OB ,∴∠PQO =∠AOB. ∵tan ∠AOB =43,∴tan ∠PQO =43.∴Rt △POQ 中,PO OQ =43,即26OQ =43.∴OQ =392,故x =392.(2)l 与AB ︵所在圆相切时,OP ⊥l ,l ∥OB ,OP =26,∠AOB =∠OQP , ∴tan ∠AOB =tan ∠OQP =43,PO PQ =43,∴QP =392.在Rt △POQ 中,PQ 2+OP 2=OQ 2,即(392)2+262=OQ 2.∴OQ =32.5.∴x min =-32.5. (3)31.5,-31.5,-16.5.周测(28.1~28.2.1)(时间:45分钟 满分:100分)一、选择题(每小题4分,共32分)1.在△ABC 中,∠C =90°,则下列等式成立的是(B)A .sinA =ACABB .sinA =BCABC .sinA =ACBCD .sinA =BCAC2.在Rt △ABC 中,∠C =90°,若AB =2,AC =1,则tanA 的值为(D)A.12B.32C.33D. 33.计算sin 245°+cos30°tan60°,其结果是(A) A .2B .1C.52D.544.在△ABC 中,∠A ,∠B ,∠C 对边分别为a ,b ,c ,a =5,b =12,c =13,下列结论成立的是(C)A .sinA =125B .cosA =513C .tanA =512D .cosB =12135.在△ABC 中,∠C =90°,BC =2,sinA =23,则边AC 的长是(A)A. 5B .3C.43D .136.如图,在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于点D.若BD ∶CD =3∶2,则tanB 的值为(D)A.32B.23C.62D.637.如图,已知AD 是△ABC 的外接圆的直径,AD =13 cm ,cosB =513,则AC 的长等于(D)A .5 cmB .6 cmC .10 cmD .12 cm8.如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积为49,则sin α-cos α=(D)A.513 B .-513C.713 D .-713二、填空题(每小题4分,共24分)9.计算:(π-3.14)0+tan6010.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC 的顶点都在格点上,则∠BAC 的正弦值511.如图,将∠AOB 放在由边长为1个单位长度的小正方形组成的网格中,则tan ∠AOB =12.12.如图,菱形ABCD 的对角线AC =6,BD =8,∠ABD =α,则tan α=34.13.如果等腰三角形的三边长分别为1,1,3,那么它的一个底角为30°.14.如图,在矩形ABCD 中,AB =6,BC =10,将矩形ABCD 沿BE 折叠,点A 落在A ′处.若EA ′的延长线恰好过点C ,则sin ∠ABE 10三、解答题(共44分) 15.(9分)计算:(1)cos45°sin45°-tan45°;解:原式=2222-1 =1-1 =0.(2)tan45°sin 260°-4sin30°cos45°+6tan30°; 解:原式=1×(32)2-4×12×22+6×33=34-2+ 2 =34. (3)(-1)2 019+2sin60°+(π-3.14)0+|-3|.解:原式=-1+2×32+1+ 3 =-1+3+1+ 3 =2 3.16.(9分)如图,在△ABC 中,AB =AC =13,BC =10,求tanB ,cosB ,sinB 的值.解:过点A 作AD ⊥BC 于点D. ∵AB =AC =13,BC =10. ∴BD =DC =12BC =5.在Rt △ABD 中, AD =AB 2-BD 2=12.∴sinB =AD AB =1213,cosB =BD AB =513,tanB =AD BD =125.17.(12分)如图,在△ABC 中,∠C =90°,点D,E 分别在AC ,AB 上,BD 平分∠ABC ,DE ⊥AB ,AE =6,cosA =35.求:(1)DE ,CD 的长; (2)tan ∠DBC 的值.解:(1)∵DE ⊥AB ,cosA =35,∴AE AD =35.又∵AE =6,∴AD =10.∴DE =8.又∵BD 平分∠ABC ,∠C =∠DEB =90°, ∴CD =DE =8,即DE =8,CD =8.(2)由(1)知AC =AD +DC =10+8=18, cosA =AC AB =35,∴18AB =35,解得AB =30.∴BE =AB -AE =30-6=24.在Rt △BCD 和Rt △BED 中,BD =BD ,CD =DE , ∴Rt △BCD ≌Rt △BED.∴BC =BE =24, ∴tan ∠DBC =CD BC =824=13.18.(14分)如图,在△ABC 中,AB =AC ,以AC 边为直径作⊙O 交BC 边于点D ,过点D 作DE ⊥AB 于点E ,ED ,AC 的延长线交于点F.(1)求证:EF 是⊙O 的切线;(2)若EB =32,且sin ∠CFD =35,求⊙O 的半径与线段AE 的长.解:(1)证明:连接OD ,∵AB =AC ,∴∠B =∠ACD. ∵OC =OD ,∴∠ODC =∠OCD. ∴∠B =∠ODC ,∴OD ∥AB. ∵DE ⊥AB ,∴OD ⊥EF. 又∵OD 是⊙O 的半径, ∴EF 是⊙O 的切线.(2)在Rt △ODF 中,sin ∠OFD =OD OF =35,设OD =3x(x>0),则OF =5x , ∴AB =AC =6x ,AF =8x.在Rt △AEF 中,∵sin ∠AFE =AE AF =35,∴AE =35×8x =245x.∵BE =AB -AE =6x -245x =65x ,∴65x =32,解得x =54. ∴AE =245×54=6,OD =3×54=154,即⊙O 的半径为154,线段AE 的长为6.28.2.2 应用举例第1课时 与视角有关的解直角三角形应用题基础题知识点1 利用解直角三角形解决简单问题1.如图,已知AC =100 m ,∠B =30°,则B ,C 两地之间的距离为(A)A.100 3 mB.50 2 mC.50 3 mD.10033m2.(2018·宜昌)如图,要测量小河两岸相对的两点P ,A 的距离,可以在小河边取PA 的垂线PB 上的一点C ,测得PC =100米,∠PCA =35°,则小河宽PA 等于(C)A.100sin35°米B.100sin55°米C.100tan35°米D.100tan55°米3.如图,一架梯子斜靠在墙上,若梯子到墙的距离AC =3米,cos ∠BAC =34,则梯子AB 的长度为4米.4.如图,某航天飞船在地球表面P 点的正上方A 处,从A 处观测到地球上的最远点Q.若∠QAP =α,地球半径为R ,则航天飞船距离地球表面的最近距离AP =Rsin α-R .5.(2017·台州)如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB 与墙MN 平行且距离为0.8米,已知小汽车车门宽AO 为1.2米,当车门打开角度∠AOB 为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)解:过点A 作AC ⊥OB ,垂足为C ,在Rt △ACO 中,∵∠AOC =40°,AO =1.2米, ∴AC =sin ∠AOC ·AO ≈0.64×1.2=0.768(米).∵汽车靠墙一侧OB 与墙MN 平行且距离为0.8米,∴车门不会碰到墙. 知识点2 利用视角解直角三角形6.(教材P78习题T3变式)如图,飞机在空中A 处探测到它的正下方地面上目标C ,此时飞行高度AC =1 200米,从飞机上看地面指挥台B 的俯角α的正切值为34,则飞机与指挥台之间的距离AB 为(D)A.1 200米B.1 600米C.1 800米D.2 000米7.(教材P75例4变式)如图,小东在教学楼距地面9米高的窗口C 处,测得正前方旗杆顶部A 点的仰角为37°,旗杆底部B 点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处.若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)解:在Rt △BCD 中,BD =9米,∠BCD =45°,则 BD =CD =9米, ∴AD =CD ·tan37°=6.75米. ∴AB =AD +BD =15.75米. 整个过程中国旗上升高度是: 15.75-2.25=13.5(米), ∵耗时45秒,∴上升速度为13.545=0.3(米/秒).答:国旗应以0.3米/秒的速度匀速上升.中档题8.(2018·广西)如图,从甲楼底部A 处测得乙楼顶部C 处的仰角是30°,从甲楼顶部B 处测得乙楼底部D 处的俯角是45°,已知甲楼的高AB 是120 m ,则乙楼的高CD 是结果保留根号)9.(2018·菏泽)2018年4月12日,菏泽国际牡丹花会拉开帷幕,菏泽电视台用直升机航拍技术全程直播.如图,在直升机的镜头下,观测曹州牡丹园A 处的俯角为30°,B 处的俯角为45°.若此时直升机镜头C 处的高度CD 为200 m ,点A ,B ,D 在同一条水平直线上,则A ,B 两点间的距离为多少米?(结果保留根号)解:由图可知,∠ECA =30°,∠ECB =45°, ∴∠ACD =60°,∠BCD =45°. 在Rt △BCD 中,DC =BD =200 m. 在Rt △ACD 中,tan ∠ACD =ADDC ,∵∠ACD =60°,DC =200 m ,∴AD =tan60°·DC =200 3 m. ∴AB =AD -BD =(2003-200)m.答:A ,B 两点间的距离为(2003-200)m.10.某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A 处水平飞行至B 处需8秒,在地面C 处同一方向上分别测得A 处的仰角为75°,B 处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)解:作AD ⊥BC 于点D ,BH ⊥水平线于点H.由题意,得∠ACH =75°,∠BCH =30°,AB ∥CH , ∴∠ABC =30°,∠ACB =45°. ∵AB =32 m ,∴AD =CD =16 m ,BD =AB ·cos30°=16 3 m. ∴BC =BD +CD =(163+16)m. ∴BH =BC ·sin30°=(83+8)m.答:这架无人机的飞行高度是(83+8)m.11.(2018·内江)如图是某路灯在铅垂面内的示意图,灯柱AC 的高为11米,灯杆AB 与灯柱AC 的夹角∠A =120°,路灯采用锥形灯罩,在地面上的照射区域DE 长为18米,从D ,E 两处测得路灯B 的仰角分别为α和β,且tan α=6,tan β=34.求灯杆AB 的长度.解:过点B 作BF ⊥CE 于点F ,过点A 作AG ⊥BF 于点G.则∠CAG =90°,∴∠BAG =∠BAC -∠CAG =30°.设AB =x ,则BG =x 2,AG =32x.∴BF =x2+11.∵DE =18,DF =BF tan α,EF =BFtan β,∴x 2+116+x 2+1134=18.∴x =2.答:灯杆AB 的长度为2米.综合题12.如图,体育场内一看台与地面所成夹角为30°,看台最低点A 到最高点B 的距离为103米,A ,B 两点正前方有垂直于地面的旗杆DE ,在A ,B 两点处用仪器测量旗杆顶端E 的仰角分别为60°和15°(仰角即视线与水平线的夹角).(1)求AE 的长;(2)已知旗杆上有一面旗在离地面1米的F 点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?解:(1)∵BG ∥CD ,∴∠GBA =∠BAC =30°. 又∵∠GBE =15°,∴∠ABE =45°. ∵∠EAD =60°,∴∠BAE = 90°.∴∠AEB =∠ABE =45°.∴AB =AE =103米. 答:AE 的长为103米.(2)在Rt △ADE 中,DE =AE ·sin60°=103×32=15(米),又∵DF =1米, ∴FE =14米.∴时间t =140.5=28(秒).答:这面旗到达旗杆顶端需要28秒.第2课时 与方位角有关的解直角三角形应用题基础题知识点 与方位角有关的应用问题1.如图,小雅家(图中点O 处)门前有一条东西走向的公路,经测得有一水塔(图中点A 处)在距离北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB 是(A)A .250米B .2503米 C.50033米D .5002米2.(2018·河北模拟)如图,在距离铁轨200米处的B 处观察由东向西的动车,当动车车头在A 处时,恰好位于B 处的北偏东60°方向上,10秒钟后,动车车头到达C 处,恰好位于B 处北偏西45°方向上,则这时段动车的平均速度是(A)A .20(3+1)米/秒B .20(3-1)米/秒C .200米/秒D .300米/秒3.(教材P77练习T1变式)(2018·成都)由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A 处时,测得小岛C 位于它的北偏东70°方向,且与航母相距80海里,再航行一段时间后到达B 处,测得小岛C 位于它的北偏东37°方向,如果航母继续航行至小岛C 的正南方向的D 处,求还需航行的距离BD 的长.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)解:由题意可知:∠ACD =70°,∠BCD =37°,AC =80海里. 在Rt △ACD 中,cos ∠ACD =CD AC ,∴0.34=CD80.∴CD =27.2海里.在Rt △BCD 中,tan ∠BCD =BD CD ,∴0.75=BD27.2.∴BD =20.4海里.答:还需航行的距离BD 的长为20.4海里.中档题4.(2018·青岛)某区域平面示意图如图,点O 在河的一侧,AC 和BC 表示两条互相垂直的公路.甲勘测员在A 处测得点O 位于北偏东45°,乙勘测员在B 处测得点O 位于南偏西73.7°,测得AC =840 m ,BC =500 m .请求出点O 到BC 的距离.(参考数据:sin73.7°≈2425,cos73.7°≈725,tan73.7°≈247)解:由点O 分别向BC ,AC 作垂线,垂足为D ,E ,则四边形OECD 为矩形.设OD =x.在Rt △ODB 中, ∠ODB =90°, ∵tan ∠OBD =ODBD ,∴BD =OD tan ∠OBD =724x ,CD =500-724x.AE =AC -EC =840-x.又∵∠OAC =45°,∠OEA =90°, ∴OE =AE =840-x.∴840-x =500-724x.解得x =480.答:点O 到BC 的距离为480米.5.(2018·河北考试说明)如图,油井A 位于油库P 南偏东75°方向,主输油管道AP =12 km ,一新建油井B 位于P 的北偏东75°方向,且位于A 的北偏西15°方向.(1)∠PBA =90°; (2)求A ,B 间的距离;(3)要在AP 上选择一个支管道连接点C ,使从B 到C 处的支输油管道最短,求这时BC 的长.(结果保留根号) 解:(2)在Rt △APB 中,∠PBA =90°,∠BPA =180°-75°-75°=30°,AP =12,∴AB =12AP =12×12=6.∴A ,B 间的距离是6 km.(3)要使B 到C 的管道最短,则BC ⊥PA 于点C. ∵∠BPA =30°,∠PBA =90°,∴∠PAB =60°. 在Rt △ABC 中,BC =AB ·sin ∠BAC =6×32=33,∴BC 的长是3 3 km.第3课时 与坡度、坡角有关的解直角三角形应用题基础题知识点 与坡度、坡角有关的应用问题1.如图,修建抽水站时,沿着坡度为i =1∶6的斜坡铺设管道,下列等式成立的是(C)A .sin α=16B .cos α=16C .tan α=16D .以上都不对2.如图,一山坡的坡度为i =1∶3,小辰从山脚A 出发,沿山坡向上走了200米到达点B ,小辰上升了100米.3.某商场为方便顾客使用购物车,准备将滚动电梯的坡面坡度由1∶1.8改为1∶2.4(如图).若改动后电梯的坡面长为13米,则改动后电梯水平宽度增加部分BC 的长为3米.4.(2018·安顺)如图是某市一座人行天桥的示意图,天桥离地面的高BC 是10米,坡面AC 的倾斜角∠CAB =45°,在距A 点10米处有一建筑物HQ ,为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面DC 的倾斜角∠BDC =30°.若新坡面下D 处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除?(计算最后结果保留一位小数,参考数据:2≈1.414,3≈1.732)解:由题意,得AH =10米,BC =10米,在Rt △ABC 中,∠CAB =45°,∴AB =BC =10(米). 在Rt △DBC 中,∠CDB =30°, ∴DB =BCtan ∠CDB=103(米).∴DH =AH -AD =AH -(DB -AB)=10-103+10=20-103≈2.7(米). ∵2.7<3,∴该建筑物需要拆除.中档题5.(2018·重庆A 卷)如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E 点处测得旗杆顶端的仰角∠AED =58°,升旗台底部到教学楼底部的距离DE =7米,升旗台坡面CD 的坡度i =1∶0.75,坡长CD =2米.若旗杆底部到坡面CD 的水平距离BC =1米,则旗杆AB 的高度约为(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)(B)A .12.6米B .13.1米C .14.7米D .16.3米6.如图,天星山山脚下西端A 处与东端B 处相距800(1+3)米,小军和小明同学分别从A 处和B 处向山顶匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为22米/秒.若小明与小军同时到达山顶C 处,则小明的行走速度是1米/秒.7.(2018·连云港)如图1,水坝的横截面是梯形ABCD ,∠ABC =37°,坝顶DC =3 m ,背水坡AD 的坡度i(即tan ∠DAB)为1∶0.5,坝底AB =14 m.(1)求坝高;(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE =2DF ,EF ⊥BF ,求DF 的长.(参考数据:sin37°≈35,cos37°≈45,tan37°≈34)解:(1)过点D 作DM ⊥AB ,垂足为M ,过点C 作CN ⊥AB ,垂足为N , ∵背水坡AD 的坡度i 为1∶0.5,∴tan ∠DAB =2. 设AM =x ,则DM =2x.又∵四边形DMNC 是矩形,∴DM =NC =2x. 在Rt △BNC 中,tan ∠ABC =tan37°=CN BN =2x BN =34,∴BN =83x.由x +3+83x =14,得x =3,∴DM =6,即坝高为6 m.(2)过点F 作FH ⊥AB ,垂足为H ,过点D 作DM ⊥AB ,垂足为M. 设DF =y ,则AE =2y. ∴EH =3+2y -y =3+y , BH =14+2y -(3+y)=11+y.由FH ⊥BE ,EF ⊥BF ,得△EFH ∽△FBH. ∴HF HB =EH FH ,即611+y =3+y 6. 解得y =-7+213或y =-7-213(舍). ∴DF =213-7.答:DF 的长为(213-7)米.河北常考点专题(八) 解直角三角形的实际应用解直角三角形的实际应用题时,要灵活运用转化思想,通常是根据以下方法和步骤解决:(1)有图的要将题干中的已知量在图中表示出来,找到与已知量和未知量相关联的三角形,画出平面几何图形,弄清楚已知条件中各量之间的关系;(2)若三角形是直角三角形,根据边角关系进行计算.若三角形不是直角三角形,可通过添加辅助线构造直角三角形来解决,其中作某边上的高是常用的辅助线. 类型1 构造单一直角三角形解决实际问题1.(2017·青海)如图所示,小芳在中心广场放风筝,已知风筝拉线长100米(假设拉线是直的),且拉线与水平地面的夹角为60°.若小芳的身高忽略不计,则风筝离水平地面的高度是(结果保留根号)2.(2018·台州)图1是一辆吊车的实物图,图2是其工作示意图,AC 是可以伸缩的起重臂,其转动点A 离地面BD 的高度AH 为3.4 m .当起重臂AC 长度为9 m ,张角∠HAC 为118°时,求操作平台C 离地面的高度.(结果保留小。

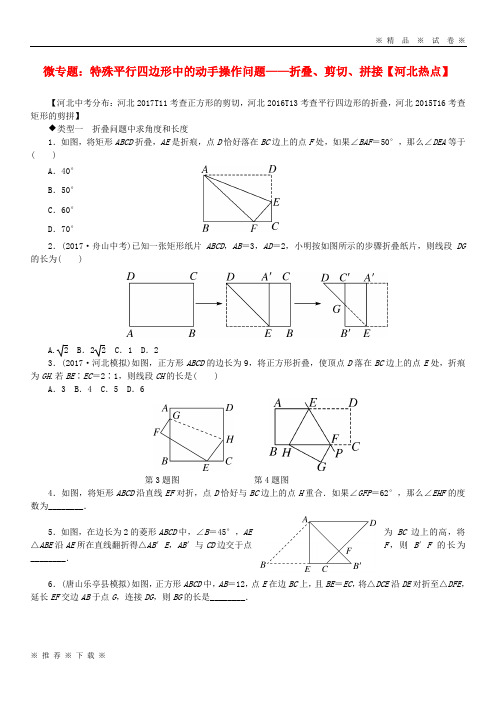
微专题:特殊平行四边形中的动手操作问题——折叠、剪切、拼接【河北热点】【河北中考分布:河北2017T11考查正方形的剪切,河北2016T13考查平行四边形的折叠,河北2015T16考查矩形的剪拼】◆类型一折叠问题中求角度和长度1.如图,将矩形ABCD折叠,AE是折痕,点D恰好落在BC边上的点F处,如果∠BAF=50°,那么∠DEA等于( )A.40°B.50°C.60°D.70°2.(2017·舟山中考)已知一张矩形纸片ABCD,AB=3,AD=2,小明按如图所示的步骤折叠纸片,则线段DG 的长为( )A. 2 B.2 2 C.1 D.23.(2017·河北模拟)如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是( )A.3 B.4 C.5 D.6第3题图第4题图4.如图,将矩形ABCD沿直线EF对折,点D恰好与BC边上的点H重合.如果∠GFP=62°,那么∠EHF的度数为________.5.如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长为________.6.(唐山乐亭县模拟)如图,正方形ABCD中,AB=12,点E在边BC上,且BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,则BG的长是________.7.(2017·定州期中)如图,把矩形ABCD沿对角线BD折叠,使点C落在点F处,BF交AD于点E.(1)求证:△BEA≌△DEF;(2)若AB=2,AD=4,求AE的长.◆类型二特殊四边形的剪切与拼接8.如图,把一张矩形纸片对折两次,然后剪下一个角,为了得到一个正方形,剪刀与折痕所成的角的度数应为( )A.30° B.45° C.60° D.90°第8题图第9题图9.(河北中考)如图,将长为2、宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n不可能是( )A.2 B.3 C.4 D.510.(河北中考)如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼成一个与原来面积相等的正方形,则( )A.甲、乙都可以B.甲、乙都不可以C.甲不可以、乙可以D.甲可以、乙不可以11.(2017·保定二模)如图,五个全等的小正方形无缝隙、不重合地拼成了一个“十字”形,连接A、B两个顶点,过顶点C作CD⊥AB,垂足为D.“十字”形被分割为了①、②、③三个部分,这三个部分恰好可以无缝隙、不重合地拼成一个矩形,这个矩形的长与宽的比为( )A.2∶1 B.10∶1 C.3∶1 D.23∶112.(2017·廊坊文安县期中)请阅读下列材料:问题:现有5个边长为1的正方形,排列形式如图甲,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中的每一个小正方形的边长均为1)中用实线画出拼接成的新正方形.小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得x= 5.由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图乙所示的分割线,拼出如图丙所示的新的正方形.请你参考小东同学的做法,解决如下问题:现有10个边长为1的小正方形,排列形式如图丁,请把它们分割后拼接成一个新的正方形.要求:在图丁中画出分割线,并在图戊的正方形网格图中用实线画出拼接成的新正方形(直接画出图形,不需写过程).13.★(2016·张家口宣化县模拟)如图,长方形纸片ABCD中,AB=8cm,AD=6cm,按下列步骤进行裁剪和拼图:第一步:如图①,在线段AD上任意取一点E,沿EB,EC剪下一个三角形纸片EBC(余下部分不再使用);第二步:如图②,沿三角形纸片EBC的中位线GH将纸片剪成两部分,并在线段GH上任意取一点M,线段BC 上任意取一点N,沿MN将梯形纸片GBCH剪成两部分;第三步:如图③,将MN左侧纸片绕G点按顺时针方向旋转180°,使线段GB与GE重合,将MN右侧纸片绕H 点按逆时针方向旋转180°,使线段HC与HE重合,拼成一个与三角形纸片EBC面积相等的四边形纸片.求拼成的这个四边形纸片的周长的最小值和最大值.参考答案与解析1.D 2.A 3.B 4.56°5.2- 2 解析:∵在边长为2的菱形ABCD 中,∠B =45°,AE 为BC 边上的高,∴AE = 2.由折叠易得△ABB ′为等腰直角三角形,∴BB ′=AB 2+AB ′2=22,∴CB ′=BB ′-BC =22-2.∵AB ∥CD ,∴∠FCB ′=∠B =45°.又由折叠的性质知,∠B ′=∠B =45°,∴△B ′CF 为等腰直角三角形,∴CF 2+B ′F 2=B ′C 2,即2B ′F 2=B ′C 2,∴B ′F =2- 2.6.8 解析:由折叠可知EF =EC =12BC =6,DF =DC =DA ,∠DFE =∠C =90°,∴∠DFG =∠A =90°.在Rt△ADG和Rt△FDG中,⎩⎪⎨⎪⎧DA =DF ,DG =DG ,∴Rt△ADG ≌Rt△FDG (HL),∴AG =FG .设AG =FG =x ,则EG =x +6,BG =12-x ,由勾股定理得EG 2=BE 2+BG 2,即(x +6)2=62+(12-x )2,解得x =4,∴AG =4,∴BG =8.7.(1)证明:∵四边形ABCD 是矩形,∴AB =CD ,∠A =∠C =90°.由折叠得FD =CD ,∠F =∠C =90°,∴AB =FD ,∠A =∠F .在△BEA 和△DEF 中⎩⎪⎨⎪⎧∠AEB =∠FED ,∠A =∠F ,AB =FD ,∴△BEA ≌△DEF .(2)解:∵△BEA ≌△DEF ,∴BE =DE =AD -AE =4-AE .设AE =x ,则BE =4-x .在Rt△BAE 中,由勾股定理得AB 2+AE 2=BE 2,∴22+x 2=(4-x )2,解得x =32,∴AE =32.8.B9.A 解析:如图,将长为2、宽为1的矩形纸片分割成n 个三角形后,拼成面积为2的正方形,则n 可以为3,4,5,故n 不可能为2.10.A 解析:所拼图形如图所示,甲、乙都可以拼成一个与原来面积相等的正方形.故选A.11.A 解析:如图,易知四边形ACBE 是正方形,AB 与CE 是正方形的对角线,则CD =DE =AD =BD ,则组成的这个矩形的长与宽的比为2∶1,故选A.12.解:如图所示.13.解:如图①为第三步剪拼之后的四边形M1N1N2M2的示意图.N1N2=EN1+EN2=NB+NC=BC,M1M2=M1G+GM+MH+M2H=2(GM+MH)=2GH=BC(三角形中位线定理).∵M1M2∥N1N2,∴四边形M1N1N2M2是平行四边形,其周长为2N1N2+2M1N1=2BC+2MN.∵BC=6为定值,∴四边形的周长取决于MN的大小.如图②是剪拼之前的完整示意图,过点G,H作BC边的平行线,分别交AB,CD于P点、Q点,则四边形PBCQ 是一个矩形,这个矩形是矩形ABCD的一半,∵M是线段PQ上的任意一点,N是线段BC上的任意一点,根据垂线段最短,得到MN的最小值为PQ与BC平行线之间的距离,即MN最小值为4;而MN的最大值等于矩形对角线的长度,即PB2+BC2=42+62=213.四边形M1N1N2M2的周长为2BC+2MN=12+2MN,∴四边形M1N1N2M2周长的最小值为12+2×4=20,最大值为12+2×213=12+413.故拼成的四边形纸片的周长的最小值为20,最大值为12+413.。