最优控制(3)

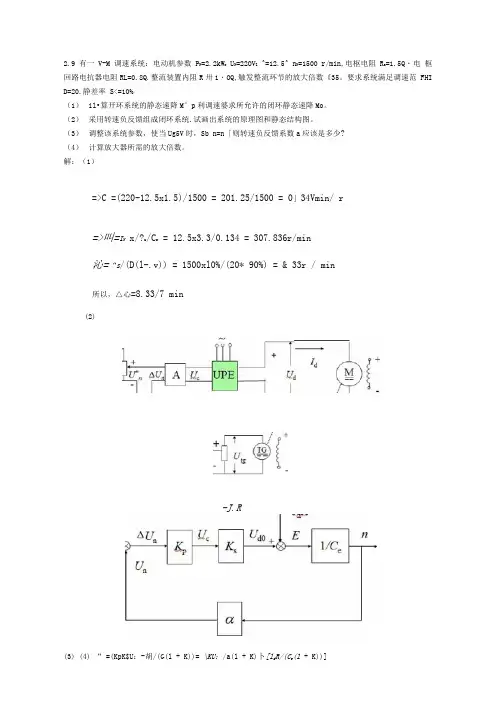
2.9 有一 V-M 调速系统：电动机参数 PN =2.2kWrUN=22OVZ^=12.5^ nN=1500 r/min,电枢电阻 Ra=1.5Q・电枢回路电抗器电阻RL=0.8Q.整流装置内阻R卅1・OQ,触发整流环节的放大倍数《35。

要求系统满足调速范 FHI D=20.静差率 S<=10%：（1）il•算开环系统的静态速降M°p利调速婆求所允许的闭环静态速降Mo。

（2）采用转速负反馈组成闭环系统.试画出系统的原理图和静态结构图。

（3）调整该系统参数，使当Ug5V时，Sb n=n「则转速负反馈系数a应该是多少?（4）计算放大器所需的放大倍数。

解：（1）=>C =(220-12.5x1.5)/1500 = 201.25/1500 = 0」34Vmin/ r=>叫=I N x/?z/C r = 12.5x3.3/0.134 = 307.836r/min沁=“s/(D(l-.v)) = 1500xl0%/(20* 90%) = & 33r / min所以，△心=8.33/7 min(2)-J.R(3) (4) “ =(KpK$U：-胡/(G(l + K))= \KU；/a(l + K)卜[l d R/(C e(l + K))]K = (% / An f/)-l = 307.836/8.33-1 = 35.955 1500 = [35.955 xl5/a(l +35.955)] - [12.5 x 3.3 /(0.134(1 + 35.955))]na = 0.0096V mill/ /•空= 35.955® 34 十34K]a 35*0.0096也可以用*11略算法:& = KC e / K 、a • Ky = 35.955 x 0.134 / (35 x 0.01) = 13.762.4 直流电动机为 P N =74kW /UN=220V, l N =378A, n N =1430r/min. Ra=0.023 Q .相控整流器内阻 Rrec=0.022 Q 。

最优控制理论与系统第三版课程设计设计背景与意义最优控制理论是现代控制领域的核心内容之一，它是将优化理论和控制理论有机结合的产物。

在工程实践中，最优控制理论被广泛应用于机械、航空、航天、自动化等领域中的复杂系统控制问题。

本次课程设计旨在通过实践，让学生更深入地理解最优控制理论的基本概念、设计方法和应用技巧，提高学生的实际操作能力和综合素质。

课程设计内容一、案例说明本次课程设计将以某飞行器为例，通过设计控制器的方式使其达到最优控制，也就是最大速度的情况下最小燃料消耗。

并根据实际系统反馈对设计的控制器进行调整优化。

二、设计流程1.建立系统模型将飞行器的状态和控制变量建立数学模型。

2.确定控制器类型选择合适的最优控制理论与方法，设计控制器。

3.模拟仿真使用Simulink软件进行模拟仿真，通过寻找最优控制策略使系统达到最优状态。

4.设计实验结合实际情况，设计并开展实验证明最优控制的效果。

三、实验要求1.独立完成实验设计、设置，唯一限制条件是实验所需资源不能超出课程要求。

2.实验完成过程中，重视记录和总结。

需要书写详细的实验报告，对实验过程、数据和分析进行说明。

3.需要根据实验结果进行总结思考，对设计控制器的方法、控制效果进行讨论。

四、实验日期本次课程设计将于X月X日开始，为期X周。

其中，模拟仿真时间1周，实验设计设置时间2周，实验完成并提交实验报告1周。

总结最优控制理论与系统课程设计是系统控制理论与工程实践的结合，是培养学生控制设计能力和解决实际问题能力的有效途径。

通过本次设计，学生将深入掌握最优控制手段，提高了实践能力，为未来工作和学习奠定了坚实基础。

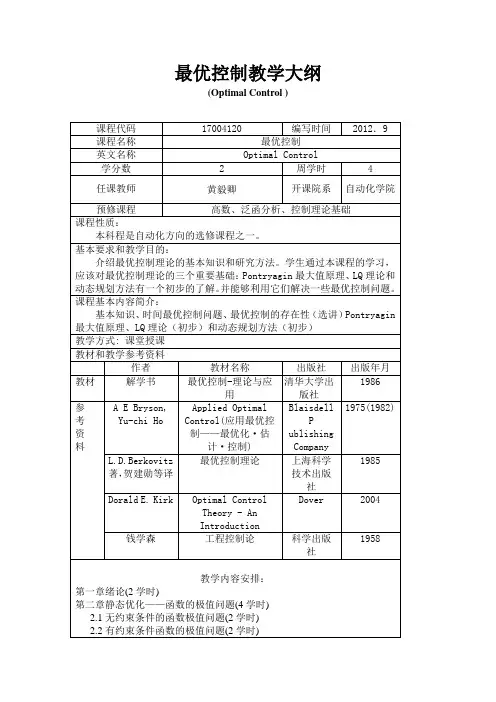
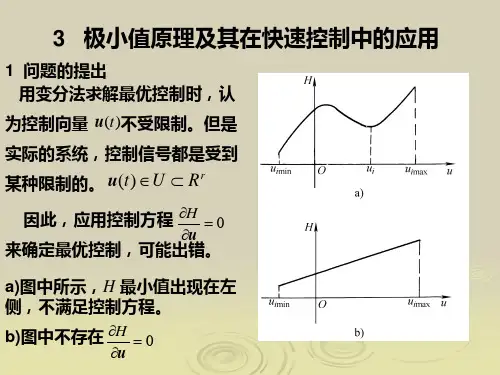
双积分系统最优控制的三次hermite配点法双积分系统最优控制的三次Hermite配点法随着科学技术的不断发展，控制理论在现代工程技术中的应用越来越广泛。

在控制理论中，最优控制理论是一种常用的控制方法，其能够使系统在输出满足一定约束条件的前提下，实现最小化某个指标的目标。

在最优控制中，配点法是一种常用的数值解法，该方法可以将最优控制转化为较为容易求解的数值计算问题。

其中，三次Hermite配点法是一种比较常用的配点法。

本文将介绍双积分系统最优控制的三次Hermite配点法及其应用。

首先，将引入双积分系统和最优控制的概念。

其次，将介绍三次Hermite配点法的基本原理和计算方法。

最后，将给出三次Hermite配点法在双积分系统最优控制中的应用实例及其优缺点。

双积分系统和最优控制的概念双积分系统是指含有两个二阶积分项的系统，其一般形式如下：$$ \begin{aligned} y(t) &=\int_{0}^{t}\int_{0}^{s} f(\tau, x(\tau)) d \tau d s \\&=\int_{0}^{t}\left[\int_{0}^{s} f(\tau, x(\tau)) d \tau\right] d s \end{aligned} $$其中，$f(\tau, x(\tau))$为系统的输入，$x(\tau)$为系统的状态。

最优控制是指，在一定约束条件下，通过调整系统的输入，使得系统的某个性能指标达到最小值。

控制系统满足最优性的条件是其状态方程必须满足哈密顿-雅可比-贝尔曼(HJB)方程。

对于双积分系统来说，其HJB方程可以表示为：$$ \frac{\partial V}{\partial t}(t, y(t))+\min _{u(t)}\left\{\frac{\partial V}{\partial y}(t,y(t)) f(t, y(t), u(t))+g(t, y(t), u(t))\right\}=0 $$其中，$V(t,y(t))$为值函数，$u(t)$为控制输入，$f(t,y(t),u(t))$为系统的状态方程，$g(t,y(t),u(t))$为系统的性能指标。

现代控制理论试题(含详细答案)一、选择题（每题5分，共25分）1. 系统的状态变量是指（）A. 系统的输入信号B. 系统的输出信号C. 系统内部描述系统行为的变量D. 系统的反馈信号答案：C2. 状态空间表达式中，系统的状态方程和输出方程分别为（）A. x(t) = Ax(t) + Bu(t)，y(t) = Cx(t) + Du(t)B. x(t) = Bu(t) + Ax(t)，y(t) = Du(t) + Cx(t)C. x(t) = Ax(t) + Bu(t)，y(t) = Du(t) + Cx(t)D. x(t) = Bu(t) + Ax(t)，y(t) = Cx(t) + Du(t)答案：A3. 系统传递函数的零点和极点分别对应于（）A. 频率响应的幅值和相位B. 频率响应的相位和幅值C. 频率响应的谐振频率和谐振峰度D. 频率响应的稳态增益和相位答案：C4. 在控制系统中，以下哪种控制器可以使系统具有无静差特性（）A. 比例控制器B. 积分控制器C. 比例-积分控制器D. 比例-微分控制器答案：C5. 状态空间表达式中，系统的可观性矩阵和可控制性矩阵分别为（）A. Q = [C A]，P = [B A]B. Q = [C A]，P = [B A^(-1)]C. Q = [C^T A^T]，P = [B^T A^T]D. Q = [C^T A^T]，P = [B^T A]答案：D6. 状态空间表达式中，系统的状态方程为______，输出方程为______。

答案：x(t) = Ax(t) + Bu(t)，y(t) = Cx(t) +Du(t)7. 系统传递函数的零点是指______，极点是指______。

答案：使传递函数等于零的频率点，使传递函数分母等于零的频率点8. 控制系统中的稳态误差与______、______和______有关。

答案：系统类型、输入信号类型、开环增益9. 状态反馈控制器的设计方法包括______、______和______。

现代控制理论试题B 卷及答案一、1 系统[]210,01021x x u y x ⎡⎤⎡⎤=+=⎢⎥⎢⎥-⎣⎦⎣⎦能控的状态变量个数是，能观测的状态变量个数是cvcvx 。

2试从高阶微分方程385y y y u ++=求得系统的状态方程和输出方程（4分/个）解 1． 能控的状态变量个数是2，能观测的状态变量个数是1。

状态变量个数是2。

…..（4分）2．选取状态变量1x y =，2x y =，3x y =，可得 …..….…….（1分）12233131835x x x x x x x u y x ===--+= …..….…….（1分）写成010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦…..….…….（1分）[]100y x = …..….…….（1分）二、1给出线性定常系统(1)()(),()()x k Ax k Bu k y k Cx k +=+=能控的定义。

（3分）2已知系统[]210 020,011003x x y x ⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦，判定该系统是否完全能观？(5分)解 1．答：若存在控制向量序列(),(1),,(1)u k u k u k N ++-，时系统从第k 步的状态()x k 开始，在第N 步达到零状态，即()0x N =，其中N 是大于0的有限数，那么就称此系统在第k 步上是能控的。

若对每一个k ，系统的所有状态都是能控的，就称系统是状态完全能控的，简称能控。

…..….…….（3分） 2.[][]320300020012 110-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=CA ………..……….（1分） [][]940300020012 3202=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=CA ……..……….（1分） ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=940320110 2CA CA C U O ………………..……….（1分） rank 2O U n =<，所以该系统不完全能观……..….…….（2分）三、已知系统1、2的传递函数分别为2122211(),()3232s s g s g s s s s s -+==++-+求两系统串联后系统的最小实现。

1. 2**'2**'*'*01min ()2y J y y y y y y dx ⎡⎤=+++⎢⎥⎣⎦⎰,若(0)y 与(2)y 任意，求*y 及(*)J y 。

解：这是端点自由问题，相应的欧拉—拉格朗日方程为：()0f d f y dt y∂∂-=∂∂即''1(1)0d y y y dt +-++=得''1y =则'1y x c =+，21212y x c x c =++由横截条件：0f y∂=∂得'1y y ++=0即21121(1)102x c x c c +++++=0x =，1210c c ++=；2x =，12350c c ++=。

联立得122,1c c =-=所以*21212y x x =-+，*'2y x =-代入得2**'2**'*'*02321()21(221)243J y y y y y y dxx x x dx⎡⎤=+++⎢⎥⎣⎦=-+-=-⎰⎰2.电枢控制的直流电动机忽略阻尼时的运动方程：()u t θ=式中，θ为转轴的角位移，()u t 为输入。

目标函数为221min ()2u J dt θ=⎰，使初态(0)1θ=及(0)1θ=转移到终态(2)0θ=及(2)0θ=，求最优控制*()u t 及最优角位移*()t θ，最优角速度*()t θ。

解： 设12,x x θθ==则122,x x x u ==。

哈密顿函数：212212H u x u λλ=++ 协态方程: 121120,0H Hx x λλλ∂∂=-==-=-=∂∂ 控制方程：20Hu uλ∂=+=∂即*2()()u t t λ=-将*()u t 代入状态方程，可得 1222121(),(),0,()x x t x t t λλλλ==-==-边界条件为1212(0)1,(0)1,(2)0,(2)0x x x x ==== 可见这是两点边值问题，对正则方程进行拉氏变换，可得11222211221()(0)()()(0)()()(0)0()(0)()sX s x X s sX s x s s s s s s λλλλλλ-=-=--=-=-联立以上四式，可解出43211221()(0)(0)(0)(0)s X s s x s x s λλ=+-+代入初始条件12(0)1,(0)1x x ==，可得1212341111()(0)(0)X s s s s sλλ=+-+ 故 2312111()1(0)(0)26x t t t t λλ=+-+同样可解得 22212322221111()(0)(0)(0)1()(0)(0)(0)2X s x s s sx t x t t λλλλ=-+=-+利用终端条件12(2)0,(2)0x x ==可得2121432(0)(0)0312(0)2(0)0λλλλ-+=-+=解得127(0)3,(0)2λλ== 1111(0)(),()(0)s t s λλλλ==；221221211()(0)(0),()(0)(0)s t t s sλλλλλλ=-=-即 127()3,()32t t t λλ==-所以：最优控制*27()()32u t t t λ=-=-+最优角位移*23171()142x t t t t θ==+-+最优角速度*2273()122x t t t θ==-+3. 222201min (2)()22.,(),(0) 1.()u s J x u t dt s t x u t x s =+==⎰为常量试求出最优控制*u ()t 及相应的轨线*()x t 。

最优控制问题的数值方法最优控制问题涉及如何通过调整系统的状态或控制变量，使得系统的性能指标达到最优。

在实际应用中，最优控制问题具有广泛的应用，例如经济管理、自动控制系统和机器人等领域。

为了解决最优控制问题，数值方法成为了一种重要的工具。

本文将介绍最优控制问题的基本概念，并重点探讨数值方法在解决最优控制问题中的应用。

一、最优控制问题概述最优控制问题可以用数学模型表示为如下形式：$$\begin{align*}\text{最小化} & \quad J(x(t), u(t)) \\\text{约束条件} & \quad \dot{x}(t) = f(x(t), u(t)), \quad t\in [t_0, t_f] \\ & \quad x(t_0) = x_0, \quad x(t_f) = x_f \\\end{align*}$$其中，$J(x(t), u(t))$表示性能指标，$x(t)$和$u(t)$分别表示系统的状态和控制变量，$f(x(t), u(t))$表示系统的动力学方程。

最优控制问题的目标是找到一个控制策略$u(t)$，使得性能指标$J$达到最小，同时满足系统的动力学方程和初始、终端条件。

二、解决最优控制问题的标准数值方法包括动态规划和最优化方法。

1. 动态规划方法动态规划方法将最优控制问题划分为多个子问题，并迭代求解每个子问题的最优解。

具体而言，动态规划方法通过构建一个值函数$V(x(t), t)$来表示从状态$x(t)$开始，在时间$t$到$t_f$的时间段内的性能指标$J$。

值函数$V(x(t), t)$满足动态规划方程：$$\begin{align*}V(x(t), t) = \min_{u(t)} \left[ J(x(t), u(t)) + \int_{t}^{t+\Delta t}V(x(t+\Delta t), \tau) d\tau \right]\end{align*}$$其中，$\Delta t$表示时间步长。