4.4 一次函数的应用 北师大版八年级教案(第1课时)(公开课)
- 格式:doc
- 大小:142.00 KB
- 文档页数:3

2017秋期八年级数学上册4.4 一次函数的应用第1课时确定一次函数的表达式教案(新版)北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017秋期八年级数学上册 4.4 一次函数的应用第1课时确定一次函数的表达式教案 (新版)北师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017秋期八年级数学上册 4.4 一次函数的应用第1课时确定一次函数的表达式教案(新版)北师大版的全部内容。
4 一次函数的应用第1课时确定一次函数的表达式【知识与技能】1.了解两个条件确定一次函数,一个条件确定正比例函数.2。
能由两个条件求出一次函数的表达式,并解决有关实际问题。
【过程与方法】经历用两个已知条件确定一次函数表达式的应用过程,提高学生研究数学问题的技能,体验数形结合,逐步学习利用这一思想分析解决问题。
【情感与态度】具体感知数形结合的思想在一次函数中的应用价值.【教学重点】根据所给信息确定一次函数的表达式。
【教学难点】灵活运用一次函数的有关知识解决相关问题.一、创设情境,导入新课我们前面学习了有关一次函数的一些知识,掌握了其关系式的特点及图象特征,并学会了已知关系式画出其图象的方法以及分析图象特征与关系式之间的联系规律.如果反过来,告诉我们有关一次函数图象的某些特征或实际问题,能否确实关系式呢?这将是我们这节课要解决的主要问题,大家可有兴趣?【教学说明】利用一次函数图象的特征和关系式的相互转化,加强学生对知识的理解.通过提问,引发同学分析思考、寻求解决问题的办法,激起学生探求知识的欲望.二、思考探究,获取新知确定一次函数的表达式。


课题:一次函数的应用(第一课时)●教学目标:知识与技能目标:1、能通过函数图象获取信息,发展形象思维。
2、能利用函数图象解决简单的实际问题,3、初步体会方程与函数的关系。
过程与方法目标:1、通过方程与函数关系的研究,建立良好的知识联系。
情感与态度目标通过函数图象解决实际问题,培养学生的数学应用能力,同时培养学生良好的环保意识和热爱生活的意识。
重点:一次函数图象的应用●难点:学会解较为复杂的一次函数的应用题.●教学流程:一、课前回顾1. 什么是一次函数?若两个变量x,y间的关系式可以表示成y=kx+b (k,b为常数,k≠0)的形式,则称y 是x的一次函数.2. 一次函数的图象是什么?一条直线常数项b决定一次函数图象与y轴交点的位置.二、情境引入探究1:某物体沿一个斜坡下滑,它的速度v (米/秒)与其下滑时间t(秒)的关系如右图所示:(1)请写出 v 与t的关系式;(2)下滑3秒时物体的速度是多少(1)请写出 v 与t的关系式;设V=kt;∵(2,5)在图象上∴由5=2k得,k=2.5∴V=2.5t(2)下滑3秒时物体的速度是多少?将3s代入V=2.5t,得V=7.5总结:确定正比例函数的表达式需要1个条件确定一次函数的表达式需要2个条件.探究1:在弹性限度内,弹簧的长度 y(厘米)是所挂物体质量 x(千克)的一次函数。
一根弹簧不挂物体时长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米。
请写出 y 与x之间的关系式,并求当所挂物体的质量为4千克时弹簧的长度。
解:设y=kx+b,根据题意,得14.5=b ①16=3k+b ②将b=14.5代入②,得k=0.5所以在弹性限度内,y=0.5x+14.5当x=4时,y=0.5×4+14.5=16.5即物体的质量为4千克时,弹簧长度为16.5厘米.总结:怎样求一次函数的表达式?这种求函数解析式的方法叫做待定系数法求一次函数的表达式的详细步骤1.设——一次函数表达式 y=kx+b或者y=kx;2.代——将点的坐标代入y=kx+b中,列出关于K、b的方程3.解——解方程求出K、b值;4.定——把求出的k、b值代回到表达式中即可.练习1:1.如图,直线l是一次函数y=kx+b的图象,求它的表达式.解:设正比例函数y=kx将点(-1,3)代入其中3=-1×k,得k=-3∴y=-3x2. 已知直线l与直线y=-2x平行,且与y轴交于点(0,2),求直线l的解析式。


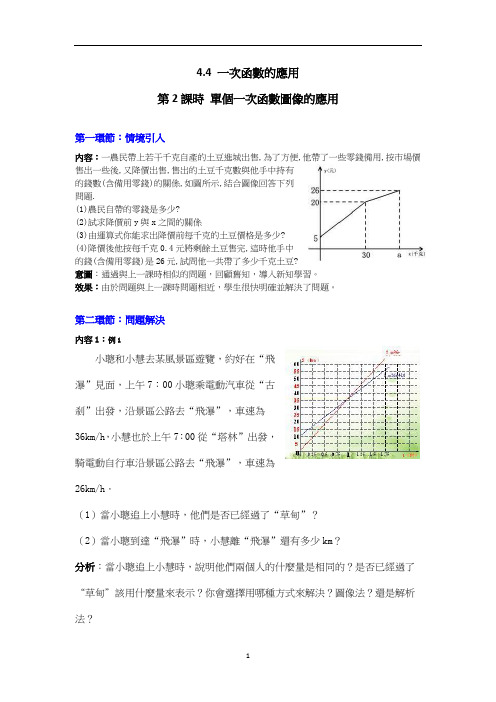
4.4 一次函數的應用第2課時單個一次函數圖像的應用第一環節:情境引入內容:一農民帶上若干千克自產的土豆進城出售,為了方便,他帶了一些零錢備用,按市場價售出一些後,又降價出售,售出的土豆千克數與他手中持有的錢數(含備用零錢)的關係,如圖所示,結合圖像回答下列問題.(1)農民自帶的零錢是多少?(2)試求降價前y與x之間的關係(3)由運算式你能求出降價前每千克的土豆價格是多少?(4)降價後他按每千克0.4元將剩餘土豆售完,這時他手中的錢(含備用零錢)是26元,試問他一共帶了多少千克土豆?意圖:通過與上一課時相似的問題,回顧舊知,導入新知學習。
效果:由於問題與上一課時問題相近,學生很快明確並解決了問題。
第二環節:問題解決內容1:例1小聰和小慧去某風景區遊覽,約好在“飛瀑”見面,上午7:00小聰乘電動汽車從“古刹”出發,沿景區公路去“飛瀑”,車速為36km/h,小慧也於上午7:00從“塔林”出發,騎電動自行車沿景區公路去“飛瀑”,車速為26km/h.(1)當小聰追上小慧時,他們是否已經過了“草甸”?(2)當小聰到達“飛瀑”時,小慧離“飛瀑”還有多少km?分析:當小聰追上小慧時,說明他們兩個人的什麼量是相同的?是否已經過了“草甸”該用什麼量來表示?你會選擇用哪種方式來解決?圖像法?還是解析法?解:設經過t時,小聰與小慧離“古刹”的路程分別為S1、S2,由題意得:S1=36t, S2=26t+10將這兩個函數解析式畫在同一個直角坐標系上,觀察圖像,得⑴兩條直線S1=36t, S2=26t+10的交點座標為(1,36)這說明當小聰追上小慧時,S1=S2=36 km,即離“古刹”36km,已超過35km,也就是說,他們已經過了“草甸”⑵當小聰到達“飛瀑”時,即S1=45km,此時S2=42.5km.所以小慧離“飛瀑”還有45-42.5=2.5(km)思考:用解析法如何求得這兩個問題的結果?小聰、小慧執行時間與路程之間的關係式分別是什麼(小聰的解析式為S1=36t,小慧的解析式為S2=26t+10)?意圖:培養學生的識圖能力和探究能力,調動學生學習的自主意識.通過問題串的精心設計,引導學生根據實際問題建立適當的函數模型,利用該函數圖像的特徵解決這個問題.在此過程中滲透數形結合的思想方法,發展學生的數學應用能力.說明:在這個環節的學習過程中,如果學生入手感到困難,可用以下問題串引導學生進行分析。
1
4.4一次函数的应用(第一课时)
教学目标:
知识与技能:
1.了解两个条件确定一个一次函数,一个条件确定一个正比例函数。
2.会利用一次函数表达式解决有关现实问题。
过程与方法:
从一次函数“数”的角度入手,转移到“形”。让学生感受确定一个函数需要两个条件,
进而探索需要哪些条件。
情感态度与价值观:
培养学生数形结合的能力,体会数学在生活中发挥着巨大的作用。
教学重难点
重点:掌握确定一个一次函数解析式的方法。
难点:将数和形建立起联系。
教学过程
(一) 课前研究:
学生自学教材89页,并完成书中问题完成课本P89“某物体沿一个斜坡下滑……”回
答:确定正比例函数的表达式需要几个条件?确定一次函数的表达式呢?
(二) 课中展示:
小组合作交流,完成问题。
小组可以对问题的结果进行互相交流,共同得出结论。
(三)应用新知:
1 在弹性限度内,弹簧的长度y(厘米)是所挂物体质量x(千克)的一次函数,一根弹簧不
挂物体时长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米。写出y与x之间的
关系式,并求当所挂物体的质量为4千克时弹簧的长度。
小组讨论,根据上面得出的结论正确完成练习。
2
2 写出满足下表的一个一次函数的解析式
x −1 0 2
y 7.5 7 6
(四)小结梳理:
已知函数图象,怎样求函数的表达式?
(1) 根据图象判断是正比例函数还是一次函数;
(2) 设出表达式;
(3) 正比例函数找出除原点外的一个点的坐标;一次函数找出两个点的坐标。(因为一
次函数的图像是一条直线,两点确定一条直线,所以需要两个条件,而正比例函数
的图像是经过原点的一条直线,所以只需要一点就可以确定这条直线。)
(五)后测达标:
1.若一次函数y = x+n的图象经过点A(−3,2),则n = __________;
2.一条直线与x轴的交点为(−3,0),与y轴的交点为(0,−7),那么这条直线对应的函数表
达式是__________,这条直线与两坐标轴围成的三角形的面积S = ________
3.已知三点(3,5),(t,9),(−4,−9)在同一直线上,则t = ________
4.已知y−2与x成正比例,当x = 3时,y = 1,求y与x之间的函数关系式。
点评:用换元的思想,将y−2看成一个整体。
(六)拓展延伸:
1.如图,已知直线2xy与x轴、y轴分别交于点A和点B,另一直线
0kbkxy
经过点C(1,0),且把△AOB分成两部分,
(1)若ΔAOB被分成的两部分的面积相等,求k和b的值;
(2)若ΔAOB被分成的两部分的面积比为1∶5,求k和b的值。
3