切线性质与判定练习题(20200930114407)

圆的切线的判定方法练习题
知识要点：
一：切线的定义：与圆有唯一公共点的直线叫做圆的切线。

二：切线的性质：圆的切线垂直于过切点的半径。

三：切线的判定：①到圆心的距离等于半径的直线是圆的切线；
②经过半径的外端，并且垂直于这条半径的直线是圆的切线。

例题讲解：
方法一：当条件不能确定直线是否有公共点时，利用“①到圆心的距离等于半径的直线是圆的切线；”证明。

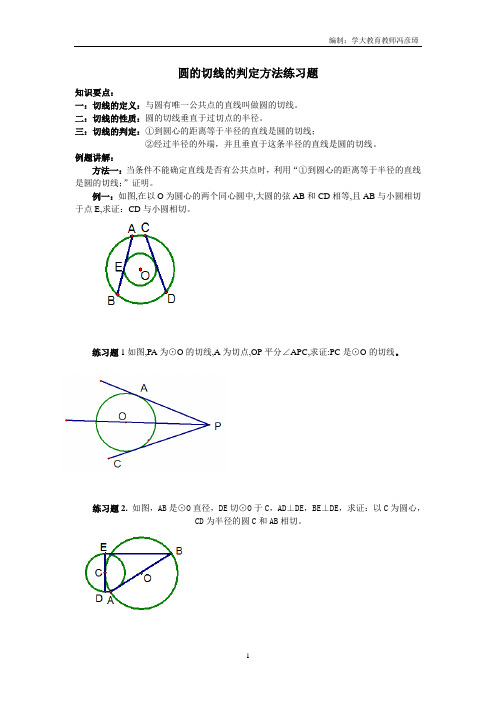
例一：如图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,求证：CD与小圆相切。

练习题1如图,PA为⊙O的切线,A为切点,OP平分∠APC,求证:PC是⊙O的切线。

练习题2.如图，AB是⊙O直径，DE切⊙O于C，AD⊥DE，BE⊥DE，求证：以C为圆心，
CD为半径的圆C和AB相切。

练习题3.如图，在以O为圆心的两个同心圆中，AB经过圆心O，且于小圆相交于点A、于大圆相交于点B。

小圆的切线AC于大圆相交于点D，且CO平分∠ACB。

（1）试判断BC所在直线与小圆的位置关系，并说明理由；
（2）试判断线段AC、AD、BC之间的数量关系，并说明理由；
（3）若AB=4cm，BC=5cm，求大圆与小圆围成的圆环的面积。

2020年人教版九年级数学上册《切线的性质与判定》夯基练习一、选择题1.如图，直线l与⊙O相切于点A，直径BC的延长线与切线l交于点D，连接AB.且∠BDA=3∠DBA，则∠DBA的度数为（）A.15°B.20°C.18°D.22°2.如图，AB是⊙O的直径，点C在⊙O上，且不与A、B两点重合，过点C的切线交AB的延长线于点D，连接AC，BC，若∠ABC=53°，则∠D的度数是（）A.16°B.18°C.26.5°D.37.5°3.如图，AB是⊙O的直径.点P、Q在⊙O上，过点P的切线与AB的延长线交于点C，连接AQ、PQ，若∠C=36°，则∠Q的度数为（）A.66°B.65°C.64°D.63°4.如图，AB是半圆O的直径，C是半圆O上一点，CD是⊙O的切线，OD∥BC，OD与半圆O交于点E，则下列结论中不一定正确的是（）A.AC⊥BCB.BE平分∠ABCC.BE∥CDD.∠D=∠A5.如图，BM与⊙O相切于点B，若∠MBA=140°，则∠ACB的度数为（）A.40°B.50°C.60°D.70°6.如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，CD与AB的延长线交于点C，∠A=30°，给出下面三个结论：①AD=CD；②BD=BC；③AB=2BC.其中正确结论的个数是( )A.3B.2C.1D.07.如图，在以点O为圆心的两个同心圆中，大圆的弦AB与小圆相切，切点为C，若大圆的半径是13，AB=24，则小圆的半径是（）A.4B.5C.6D.7二、填空题8.如图，AB是⊙O的直径，O是圆心，BC与⊙O切于点B，CO交⊙O于点D，且BC=8，CD=4，那么⊙O的半径是______．9.如图，线段AB与⊙O相切于点B，线段AO与⊙O相交于点C，AB=12，AC=8，则⊙O的半径为________.10.在周长为26π的⊙O中，CD是⊙O的一条弦，AB是⊙O的切线，且AB∥CD，若AB和CD之间的距离为18，则弦CD的长为________.11.如图，BD是⊙O的直径，BA是⊙O的弦，过点A的切线交BD延长线于点C，OE⊥AB于E，且AB=AC，若CD=2，则OE的长为.12.如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，P为切点，如果，小圆半径为3cm，那么大圆半径为 cm.13.把球放在长方体纸盒内，球的一部分露出盒外，其主视图如图．⊙O与矩形ABCD的边BC，AD分别相切和相交（E，F是交点），已知EF=CD=8，则⊙O的半径为．14.如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（﹣3，0），将⊙P沿x轴正方向以0.5个单位/秒的速度平移，使⊙P与y轴相切，则平移的时间为秒.三、解答题15.如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C．（1）若∠ADE=25°，求∠C的度数；（2）若AC=4，CE=2，求⊙O半径的长．16.如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且∠DBC=∠A，连接OE延长与圆相交于点F，与BC相交于点C．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为6，BC=8，求弦BD的长．17.如图，⊙O的直径AB的长为2，点C在圆周上，∠CAB=30°，点D是圆上一动点，DE∥AB交CA的延长线于点E，连接CD，交AB于点F．（1）如图1，当∠ACD=45°时，请你判断DE与⊙O的位置关系并加以证明；（1）如图2，当点F是CD的中点时，求△CDE的面积．18.已知，如图，AB是⊙O的直径，AD平分∠BAC交⊙O于点D，过点D的切线交AC的延长线于E．求证：DE⊥AE．19.如图，AB是半圆O的直径，C是半圆O上的一点，CF切半圆O于点C，BD⊥CF于为点D，BD与半圆O交于点E.（1）求证：BC平分∠ABD.（2）若DC=8，BE=4，求圆的直径.20.已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C.（1）如图①，若∠P=35°，求∠ABP的度数；（2）如图②，若D为AP的中点，求证：直线CD是⊙O的切线.参考答案1.答案为：C2.答案为：A3.答案为：D4.答案为：C5.答案为：A6.答案为：A.7.答案为：B.8.答案为：69.答案为：5；10.答案为：24；11.答案为：12.答案为：5；13.答案为：5．14.答案为：2或1015.解：（1）连接OA，∵∠ADE=25°，∴由圆周角定理得：∠AOC=2∠ADE=50°，∵AC切⊙O于A，∴∠OAC=90°，∴∠C=180°﹣∠AOC﹣∠OAC=180°﹣50°﹣90°=40°；（2）设OA=OE=r，在Rt△OAC中，由勾股定理得：OA2+AC2=OC2，即r2+42=（r+2）2，解得：r=3，答：⊙O半径的长是3．16.（1）证明：连接OB，如图所示：∵E是弦BD的中点，∴BE=DE，OE⊥BD，=，∵∠DBC=∠A，∴∠BOE=∠DBC，∴∠OBE+∠DBC=90°，∴∠OBC=90°，即BC⊥OB，∴BC是⊙O的切线；（2）解：∵OB=6，BC=8，BC⊥OB，∴OC==10，∵△OBC的面积=OC•BE=OB•BC，∴BE===4.8，∴BD=2BE=9.6，即弦BD的长为9.6．17.解：（1）如图1中，连接OD．∵∠C=45°，∴∠AOD=2∠C=90°，∵ED∥AB，∴∠AOD+∠EDO=180°，∴∠EDO=90°，∴ED⊥OD，∴ED是⊙O切线．（2）如图2中，连接BC，∵CF=DF，∴AF⊥CD，∴AC=AD，∴∠ACD=∠ADC，∵AB∥ED，∴ED⊥DC，∴∠EDC=90°，在RT△ACB中，∵∠ACB=90°，∠CAB=30°，AB=2，∴BC=1，AC=，∴CF=AC=，CD=2CF=，在RT△ECD中，∵∠EDC=90°，CD=，∠E=∠CAB=30°，∴S△ECD=．18.证明：连接OD．∵DE是⊙O的切线，∴OD⊥DE，∴∠ODE=90°，∵OA=OD，∴∠OAD=∠ODA，∵AD平分∠BAC，∴∠CAD=∠DAB，∴∠CAB=∠ADO，∴OD∥AE，∴∠E+∠ODE=180°，∴∠E=90°，∴DE⊥AE．19.（1）证明：连结OC，如图，∵CD为切线，∴OC⊥CD，∵BD⊥DF，∴OC∥BD，∴∠1=∠3，∵OB=OC，∴∠1=∠2，∴∠2=∠3，∴BC平分∠ABD；（2）解：连结AE交OC于G，如图，∵AB为直径，∴∠AEB=90°，∵OC∥BD，∴AG=EG，易得四边形CDEG为矩形，∴GE=CD=8，∴AE=2EG=16，在Rt△ABE中，AB==4，即圆的直径为4.20.（1）解：∵AB是⊙O的直径，AP是⊙O的切线，∴AB⊥AP，∴∠BAP=90°；又∵∠P=35°，∴∠AB=90°﹣35°=55°.（2）证明：如图，连接OC，OD、AC.∵AB是⊙O的直径，∴∠ACB=90°（直径所对的圆周角是直角），∴∠ACP=90°；又∵D为AP的中点，∴AD=CD（直角三角形斜边上的中线等于斜边的一半）；在△OAD和△OCD中，，∴△OAD≌△OCD（SSS），∴∠OAD=∠OCD（全等三角形的对应角相等）；又∵AP是⊙O的切线，A是切点，∴AB⊥AP，∴∠OAD=90°，∴∠OCD=90°，即直线CD是⊙O的切线.。

切线的性质与判定、切线长定理专题班级：姓名：1、切线的性质例1：（1）AB是⊙O的直径，PA切⊙O于点A，PO交⊙O于点C；连接BC，若∠P=40°，则∠B等于 . （2）．如图，在矩形ABCD中，AB=6，AD=10，AD，AB，BC分别与⊙O相切于E、F、G三点，过点D作⊙O的切线交BC于点M，且点为N，则DM的长为（）A． B．8 C． D．2（1）（2）练习：1、如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=115°，过D点的切线PD与射线BA交于点P，则∠ADP的度数为；2．如图，AB是⊙的直径，CD是∠ACB的平分线交⊙O于点D，过D作⊙O的切线交CB的延长线于点E．若AB=4，∠E=75°，则CD的长为；3．如图，在平面直角坐标系xOy中，⊙P的圆心是（2，a）（a＞0），半径是2，与y轴相切于点C，直线y=x被⊙P截得的弦AB的长为，则a的值是（）A． B． C． D．（1）（2）（3）4．如图，在矩形ABCD中，AD=8，E是边AB上一点，且AE=AB．⊙O经过点E，与边CD所在直线相切于点G（∠GEB为锐角），与边AB所在直线交于另一点F，且EG：EF=：2．当⊙O与边BC所在的直线与相切时，则AB的长是．5．如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CA，CB分别相交于点P，Q，则线段PQ的最小值（） A．5 B．4 C．4.75 D．4.82、切线的判定例2：(1)如图，在Rt△ABC中，∠B=90°，∠BAC的平分线交BC于点D，E为AB上的一点，DE=DC，以D 为圆心，DB长为半径作⊙D，AB=10，EB=6．（1）求证：AC是⊙D的切线；（2）求线段AC的长．(2)如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C 作CD⊥PA，垂足为D．（1）求证：CD为⊙O的切线；（2）若DC+DA=6，⊙O的直径为10，求AB的长度．练习：1．已知：如图，四边形ABCD为菱形，△ABD的外接圆⊙O与CD相切于点D，交AC于点E．（1）判断⊙O与BC的位置关系，并说明理由；（2）若CE=2，求⊙O的半径r．3、切线长定理例3：（P102，第11题）若AB、BC、CD分别与⊙O相切于E、F、G 三点，且AB∥CD，BO=6,CO=8.(1)求∠BOC的度数；（2）求BC的长；（3）求半径OF的长；（4）E、O、G共线吗？说明理由.(5)连接G、F,求证OB∥FG(6)连接EF 、GF 分别交OB 于P ，交OC 于Q,求证：四边形OPFQ 为矩形.(7)若延长CO 交⊙O 于点M ，过点M 作MN ∥OB 交CD 于点N ，求MN 的长．变式1．如图，在直角梯形ABCD 中，AD ∥BC ，∠ABC=90°，AB=12cm ，AD=8cm ，BC=22cm ，AB 为⊙O 的直径，动点P 从点A 开始沿AD 边向点D 以1cm/s 的速度运动，动点Q 从点C 开始沿CB 边向点B 以2cm/s 的速度运动．P 、Q 分别从点A 、C 同时出发，当其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t （s ）．（1）当t 为何值时，四边形PQCD 为平行四边形？（2）当t 为何值时，PQ 与⊙O 相切？变式2．如图，四边形ABCD 中，AD 平行BC ，∠ABC=90°，AD=2，AB=6，以AB 为直径的半⊙O 切CD 于点E ，F 为弧BE 上一动点，过F 点的直线MN 为半⊙O 的切线，MN 交BC 于M ，交CD 于N ，则△MCN 的周长为（ ）A ．9B ．10C ．3D ．2（变式2） （变式3） （变式4） （变式5） 变式3．如图，正方形ABCD 边长为4cm ，以正方形的一边BC 为直径在正方形ABCD 内作半圆，过A 作半圆的切线，与半圆相切于F 点，与DC 相交于E 点，则△ADE 的面积（ ）A ．12B ．24C ．8D ．6变式4．如图，PA 、PB 、分别切⊙O 于A 、B 两点，∠P=40°，则∠C 的度数为 ;变式5．如图，PA 、PB 、CD 分别切⊙O 于A 、B 、E ，CD 交PA 、PB 于C 、D 两点，若∠P=40°，则∠PAE+∠PBE 的度数为PQ变式6．如图，在平面直角坐标系xOy中，直线AB经过点A（6，0）、B（0，6），⊙O的半径为2（O为坐标原点），点P是直线AB上的一动点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（）A．B．3 C．3 D．（变式6） (例4)4、动态问题例4：如图，直线AB、CD相交于点O，∠AOC=30°，半径为1cm的⊙P的圆心在射线OA上，且与点O的距离为6cm，如果⊙P以1cm/s的速度沿由A向B的方向移动，那么⊙P与直线CD相切时运动时间是 s.练习：1．如图，⊙O的半径OC=5cm，直线l⊥OC，垂足为H，且l交⊙O于A、B两点，AB=8cm，则l沿OC所在直线平移后与⊙O相切，则平移的距离是 cm.(1题) (2题)2．如图，∠AOB=60°，点M是射线OB上的点，OM=4，以点M为圆心，2cm为半径作圆．若OA绕点O按逆时针方向旋转，当OA和⊙M相切时，OA旋转的角度是．变式：如2题图，已知∠AOB=60°，M为OB边上一点，以M为圆心、2cm为半径作⊙M．若⊙M在OB边上运动，则当OM= cm时，⊙M与OA相切．3．如图，P为正比例函数y=x图象上的一个动点，⊙P的半径为3，设点P的坐标为（x，y）．则⊙P与直线x=2相切时点P的坐标为．4．如图，已知⊙P的半径为2，圆心P在抛物线y=﹣1上运动，当⊙P与x轴相切时，圆心P的坐标为．。

切线的判定练习题切线的判定练习题切线是数学中的一个重要概念，它在几何学、微积分和物理学中都有广泛的应用。

切线的判定是切线问题中的基本内容，掌握切线的判定方法对于解决相关问题至关重要。

本文将通过一些练习题来帮助读者更好地理解和掌握切线的判定。

题目一：给定函数y = x^2 + 2x + 1，判断点P(1, 4)是否在曲线y = x^2 + 2x + 1上，并求出曲线在点P处的切线方程。

解析：首先，我们将点P的坐标代入函数y = x^2 + 2x + 1中，得到y = 1^2 + 2 × 1 + 1 = 4。

由此可知，点P在曲线y = x^2 + 2x + 1上。

接下来，我们需要求出曲线在点P处的切线方程。

切线的斜率可以通过求函数在该点的导数来得到。

对函数y = x^2 + 2x + 1求导得到y' = 2x + 2。

将x = 1代入导数表达式中，得到斜率k = 2 × 1 + 2 = 4。

切线方程的一般形式为y - y1 = k(x - x1)，其中(x1, y1)为切点的坐标。

代入点P 的坐标和斜率k，得到切线方程为y - 4 = 4(x - 1)。

题目二：已知函数y = 3x^3 - 4x^2 + 2x + 1，求曲线y = 3x^3 - 4x^2 + 2x + 1在点Q(2, 19)处的切线方程。

解析：与题目一类似，首先将点Q的坐标代入函数y = 3x^3 - 4x^2 + 2x + 1中，得到y = 3 × 2^3 - 4 × 2^2 + 2 × 2 + 1 = 19。

因此，点Q在曲线y =3x^3 - 4x^2 + 2x + 1上。

接下来，我们需要求出曲线在点Q处的切线方程。

对函数y = 3x^3 - 4x^2 + 2x + 1求导得到y' = 9x^2 - 8x + 2。

将x = 2代入导数表达式中，得到斜率k =9 × 2^2 - 8 × 2 + 2 = 14。

小专题(九) 切线的性质与判定1．(衡阳中考改编)如图，AB是⊙O的直径，点C、D为半圆O的三等分点，过点C作CE⊥AD，交AD的延长线于点E.求证：CE为⊙O的切线．2．(天津中考)已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D.当直线l与⊙O 相切于点C时，若∠DAC＝30°，求∠BAC的大小．3．如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的直线互相垂直，垂足为D，且AC平分∠DAB.(1)求证：DC为⊙O的切线；(2)若⊙O的半径为3，AD＝4，求AC的长．4．如图，已知BC是⊙O的直径，AC切⊙O于点C，AB交⊙O于点D，E为AC 的中点，连接DE.(1)若AD＝DB，OC＝5，求切线AC的长；(2)求证：ED是⊙O的切线．5．(天水中考)如图，点D为⊙O上一点，点C在直径BA的延长线上，且∠CDA ＝∠CBD.(1)判断直线CD和⊙O的位置关系，并说明理由；(2)过点B作⊙O的切线BE交直线CD于点E，若AC＝2，⊙O的半径是3，求BE 的长．6．已知：△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F，连接DF.(1)求证：直线EF是⊙O的切线；(2)当直线DF与⊙O相切时，求⊙O的半径．7．(江西中考)如图，AB 是⊙O 的直径，点P 是弦AC 上一动点(不与A 、C 重合)，过点P 作PE ⊥AB ，垂足为E ，射线EP 交AC ︵于点F ，交过点C 的切线于点D. (1)求证：DC ＝DP ；(2)若∠CAB ＝30°，当F 是AC ︵的中点时，判断以A 、O 、C 、F 为顶点的四边形是什么特殊四边形？说明理由．参考答案1．证明：连接OD.∵点C 、D 为半圆O 的三等分点，∴∠BOC ＝12∠BOD.∵∠BAD＝12∠BOD ，∴∠BOC ＝∠BAD.∴AE ∥OC.∵AD ⊥EC ，∴OC ⊥EC.∴CE 为⊙O 的切线．2．连接OC.∵直线l 与⊙O 相切于点C ，∴OC ⊥l.又∵AD ⊥l ，∴AD ∥OC.∴∠ACO ＝∠DAC.∵在⊙O 中，OA ＝OC ，∴∠BAC ＝∠ACO.∴∠BAC ＝∠DAC ＝30°. 3．(1)证明：连接OC.∵OC ＝OA ，∴∠OAC ＝∠OCA.又∵∠OAC ＝∠DAC ，∴∠DAC ＝∠OCA.∴OC ∥AD.∴OC ⊥CD.∴OC 为⊙O 的切线．(2)连接BC.由(1)知△ADC ∽△ACB ，∴AD AC ＝AC AB ，即AC 2＝AD ·AB.又∵⊙O 的半径为3，∴AB ＝6，AD ＝4.∴AC ＝2 6.4．(1)连接CD.∵BC 是⊙O 的直径，∴∠BDC ＝90°，即CD ⊥AB.∵AD ＝DB ，∴AC ＝BC ＝2OC ＝10.(2)证明：连接OD.∵∠ADC ＝90°，E 为AC 的中点，∴DE ＝EC ＝12AC.∴∠EDC ＝∠ECD.∵OD ＝OC ，∴∠ODC ＝∠OCD.∵AC 切⊙O 于点C ，∴AC ⊥OC.∴∠EDC ＋∠ODC ＝∠ECD ＋∠OCD ＝90°，即DE ⊥OD.∴ED 是⊙O 的切线．5．(1)直线CD 和⊙O 的位置关系是相切．理由：连接OD.∵AB 是⊙O 的直径，∴∠ADB ＝90°.∴∠DAB ＋∠DBA ＝90°.∵∠CDA ＝∠CBD ，∴∠DAB ＋∠CDA ＝90°.∵OD ＝OA ，∴∠DAB ＝∠ADO.∴∠CDA ＋∠ADO ＝90°，即OD ⊥CE.∴直线CD 是⊙O 的切线，即直线CD 和⊙O 的位置关系是相切．(2)∵AC ＝2，⊙O 的半径是3，∴OC ＝2＋3＝5，OD ＝3.∴CD ＝4.∵CE 切⊙O 于D ，EB 切⊙O 于B ，∴DE ＝EB ，∠CBE ＝90°.设DE ＝EB ＝x ，在Rt △CBE 中，由勾股定理，得CE 2＝BE 2＋BC 2，则(4＋x)2＝x 2＋(5＋3)2.解得x ＝6，即BE ＝6.6．(1)证明：连接OE ，则OB ＝OE.∵△ABC 是等边三角形，∴∠ABC ＝∠C ＝60°.∴△OBE 是等边三角形．∴∠OEB ＝∠C ＝60°.∴OE ∥AC.∵EF ⊥AC ，∴∠EFC ＝90°.∴∠OEF ＝∠EFC ＝90°.∴EF 是⊙O 的切线．(2)∵DF 是⊙O 的切线，∴∠ADF ＝90°.设⊙O 的半径为r ，则BE ＝r ，EC ＝4－r ，AD ＝4－2r.在Rt △ADF 中，∵∠A ＝60°，∴AF ＝2AD ＝8－4r.∴FC ＝4－(8－4r)＝4r －4.在Rt △CEF 中，∵∠C ＝60°，∴EC ＝2FC.∴4－r ＝2(4r －4)，解得r ＝43.∴⊙O 的半径是43.7．(1)证明：连接OC.∵CD 是⊙O 的切线，∴OC ⊥CD.∴∠OCD ＝90°.∴∠DCA ＝90°－∠OCA.又PE ⊥AB ，点D 在EP 的延长线上，∴∠DEA ＝90°.∴∠DPC ＝∠APE ＝90°－∠OAC.∵OA ＝OC ，∴∠OCA ＝∠OAC.∴∠DCA ＝∠DPC.∴DC ＝DP. (2)四边形AOCF 是菱形．理由：连接CF 、AF 、OF.∵F 是AC ︵的中点，∴AF ︵＝CF ︵.∴AF ＝FC.∵∠BAC ＝30°，∴∠BOC ＝60°.又AB 是⊙O 的直径，∴∠AOC ＝120°.∴∠AOF ＝∠COF ＝60°.∴△AOF 、△COF 是等边三角形．∴AF ＝FC ＝OC ＝OA.∴四边形AOCF 是菱形．。

2020-2021学年中考数学培优训练讲义（五）《圆的切线的性质与判定》专题训练班级姓名座号成绩1.如图，AB是⊙O的直径，弦CD与AB相交，连接CO，过点D作⊙O的切线，与AB的延长线交于点E，若DE∥AC，∠BAC＝40°，则∠OCD的度数为2.如图，直线AB、CD相交于点O，∠AOC＝30°，半径为2cm的⊙P的圆心在射线OA上，且与点O 的距离为6cm，如果P以1cm/s的速度沿直线AB由A向B的方向移动，那么⊙P与直线CD相切时，⊙P运动的时间是．（第1题图）（第2题图）（第3题图）3.如图，AB为半圆O的直径，AD、BC分别切⊙O于A，B两点，CD切⊙O于点E，AD与CD相交于D，BC与CD相交于C，连结OD、OE、OC，对于下列结论：①AD+BC=CD；②∠DOC=90°；③S梯形ABCD=CD•OA；④OD CDDE OD．其中结论正确的有（填序号）4.如图，在△ABC中，∠C=90°，∠BAC的平分线AD交BC于D，过点D作DE⊥AD交AB于点E，以AE为直径作⊙O．（1）求证：BC是⊙O的切线；（2）若AC=6，BC=8，求BE的长度．5．如图，AB是⊙O的直径，过点B作⊙O的切线BM，点C为BM上一点，连接AC与⊙O交于点D，E为⊙O上一点，且满足∠EAC＝∠ACB，连接BD，BE．（1）求证：∠ABE＝2∠CBD；（2）过点D作AB的垂线，垂足为F，若AE＝6，BF＝，求⊙O的半径长．6．如图，已知：C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B点的切线相交于点D，E为CH中点，连接AE并延长交BD于点F，直线CF交直线AB于点G．（1）求证：点F是BD中点；（2）求证：CG是⊙O的切线；（3）若FB = FE = 2，求⊙O的半径．作业思考：如图1，A为⊙O的弦EF上的一点，OB是和这条弦垂直的半径，垂足为H，BA的延长线交⊙O于点C，过点C作⊙O的切线与EF的延长线相交于点D．（1）求证：DA=DC；（2）当DF：EF= 1：8，且DF=时，求AB•AC的值；（3）将图1中的EF所在直线往上平行移动到⊙O外，如图2的位置，使EF与OB，延长线垂直，垂足为H，A为EF上异于H的一点，且AH小于⊙O的半径，AB的延长线交⊙O于C，过C作⊙O的切线交EF于D．试猜想DA=DC是否仍然成立？并证明你的结论．【答案】5．解：（1）∵AB是⊙O的直径，∴∠ADB＝90°，即∠DAB+∠DBA＝90°，∵BM是⊙O的切线，∴AB⊥BC，∴∠ABC＝90°，即∠CBD+∠DBA＝90°，∴∠DAB＝∠CBD，∵∠ABC＝90°，∴∠ACB＝90°﹣∠BAC，∵∠EAC＝∠ACB，∴∠EAC＝90°﹣∠BAC＝90°﹣（∠EAC﹣∠BAE），∴∠BAE＝2∠EAC﹣90°，∵AB是直径，∴∠AEB＝90°，∴∠ABE＝90°﹣∠BAE＝90°﹣（2∠EAC﹣90°）＝2（90°﹣∠EAC）＝2（90°﹣∠ACB）＝2∠CAB＝2∠CBD．∴∠ABE＝2∠CBD；（2）如图，连接DO并延长交AE于点G，∵∠DOB＝2∠BAD，∠ABE＝2∠CAB，∴∠DOB＝∠ABE，∴DG∥BE，∴∠AGO＝∠AEB＝90°，∴AG＝EG＝AE＝3，∠AOG＝∠DOF，OA＝OD，∴△AOG≌△DOF（AAS）∴DF＝AG＝3，又OF＝OB﹣BF＝OD﹣，在Rt△DOF中，根据勾股定理，得OD2＝DF2+OF2，即OD2＝32+（OD﹣）2，解得OD＝．答：⊙O的半径长为．6．（1）证明：∵CH⊥AB，DB⊥AB，∴△AEH∽△AFB，△ACE∽△ADF；（1分）∴．∵HE=EC，∴BF=FD，即点F是BD中点．（2）证明：连接CB、OC；∵AB是直径，∴∠ACB=90°．∵F是BD中点，∴∠BCF=∠CBF=90°﹣∠CBA=∠CAB=∠ACO．∴∠OCF=90°，又∵OC为圆O半径，∴CG是⊙O的切线．（6分）（3）解：∵FC=FB=FE，∴∠FCE=∠FEC．（7分）∵∠FEC=∠AEH，∴∠FCE=∠AEH，∵∠G+∠FCE=90°，∠FAB+∠AEH=90°，∴∠G=∠FAB，∴FA=FG，∵FB⊥AG，∴AB=BG．（8分）∵（2+FG）2=BG×AG=2BG2①BG2=FG2﹣BF2②由①、②得：FG2﹣4FG﹣12=0∴FG1=6，FG2=﹣2（舍去）∴AB=BG=．∴⊙O半径为2．（10分）作业思考：（1）证明：如图1，连接OC，则OC⊥DC，∴∠DCA=90°﹣∠ACO = 90°﹣∠B．∵∠DAC=∠BAE= 90°﹣∠B，∴∠DAC=∠DCA．∴DA=DC．（2）解：如图1，∵DF：EF=1：8，∵DF=，∴EF= 8DF= 8．∵DC为⊙O的切线，∴DC2 = DF•DE = ×9= 18．∴DC=3，∴AF=2，AE=6．∴AB•AC = AE•AF = 24．（3）解：答：结论DA=DC仍然成立．理由如下：如图2，延长BO交⊙O于K，连接CK，则∠KCB=90°；∵DC为⊙O的切线，∴∠DCA=∠CKB=90°﹣∠CBK．∵∠CBK=∠HBA，∴∠BAH=90°﹣∠HBA=90°﹣∠CBK．∴∠DCA=∠BAH．∴DA=DC．。

2020年九年级数学中考压轴专题：切线的性质与判定（含答案）切线的性质1.如图1,在Rt△ABC中,∠ABC=90°,以AB为直径作☉O,点D为☉O上一点,且CD=CB,连接DO并延长交CB 的延长线于点E.(1)判断直线CD与☉O的位置关系,并说明理由;(2)若BE=2,DE=4,求☉O的半径及AC的长.图12.如图2,在△ABC中,AB=AC,以AB为直径的☉O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.(1)判断DH与☉O的位置关系,并说明理由;(2)求证:点H为CE的中点.图23.如图3,BE是☉O的直径,点A和点D是☉O上的两点,过点A作☉O的切线交BE的延长线于点C.(1)若∠ADE=25°,求∠C的度数;(2)若AB=AC,CE=2,求☉O的半径长.图34.如图4,AB是☉O的直径,点C为☉O上一点,CN为☉O的切线,OM⊥AB于点O,分别交AC,CN于D,M两点.(1)求证:MD=MC;(2)若☉O的半径为5,AC=4√5,求MC的长.图4|类型2| 切线的判定5.如图5,☉O与△ABC的AC边相切于点C,与AB,BC边分别交于点D,E,DE∥OA,CE是☉O的直径.(1)求证:AB是☉O的切线;(2)若BD=4,CE=6,求AC的长.图56.如图6,△ABC内接于☉O,∠B=60°,CD是☉O的直径,点P是CD延长线上一点,且AP=AC.(1)求证:P A是☉O的切线;(2)若PD=√5,求☉O的直径.图67.如图7,点P在☉O外,PC是☉O的切线,C为切点,直线PO与☉O相交于点A,B.(1)若∠A=30°,求证:P A=3PB;(2)小明发现,∠A在一定范围内变化时,始终有∠BCP=1(90°-∠P)成立.请你写出推理过程.2图78.如图8,BD是☉O的直径,弦BC与OA相交于点E,AF与☉O相切于点A,交DB的延长线于点F,∠F=30°,∠BAC=120°,BC=8.(1)求∠ADB的度数;(2)求AC的长度.图8【参考答案】1.解:(1)直线CD与☉O相切.理由如下:连接CO.∵点D在圆上,∴OD=OB,又∵CD=CB,CO=CO,∴△COD≌△COB(SSS).∵∠ABC=90°,∴∠ODC=∠ABC=90°,∴OD⊥DC,∴直线CD与☉O相切.(2)设☉O的半径为x,∵DE=4,∴OE=4-x.在Rt△OBE中,BE2+BO2=OE2,即22+x2=(4-x)2,解得x=1.5,∴OD=OB=1.5.AB=2OB=3.∵CB,CD是圆的切线,∴CB=CD.则设CB=CD=y,在Rt△CDE中,CD2+DE2=CE2,即y2+42=(y+2)2,解得y=3,∴BC=3.在Rt△ABC中,AC=√AB2+BC2=3√2.2.(1)连接OD,AD,先利用圆周角定理得到∠ADB=90°,再根据等腰三角形的性质得BD=CD,再证明OD为△ABC 的中位线得到OD∥AC,根据DH⊥AC,所以OD⊥DH,然后根据切线的判定定理可判断DH为☉O的切线. (2)连接DE,由圆内接四边形的性质得∠DEC=∠B,再证明∠DEC=∠C,然后根据等腰三角形的性质得到CH=EH.解:(1)DH与☉O相切.理由如下:连接OD,AD,如图,∵AB为直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=CD,而AO=BO,∴OD为△ABC的中位线,∴OD∥AC,∵DH⊥AC,∴OD⊥DH,∴DH为☉O的切线.(2)证明:连接DE,如图,∵四边形ABDE为☉O的内接四边形,∴∠DEC=∠B,∵AB=AC,∴∠B=∠C,∴∠DEC=∠C,∵DH⊥CE,∴CH=EH,即H为CE的中点.3.解:(1)如图,连接OA,∵AC为☉O的切线,OA是☉O的半径,∴OA⊥AC.∴∠OAC=90°.∵∠ADE=25°,∴∠AOE=2∠ADE=50°.∴∠C=90°-∠AOE=90°-50°=40°. (2)∵AB=AC,∴∠B=∠C.∵∠AOC=2∠B,∴∠AOC=2∠C.∵∠OAC=90°,∴∠AOC+∠C=90°,∴3∠C=90°,∠C=30°.OC.∴OA=12设☉O 的半径为r , ∵CE=2,∴r=12(r +2).∴r=2.∴☉O 的半径为2. 4.解:(1)证明:连接OC , ∵CN 为☉O 的切线, ∴OC ⊥CM ,∴∠OCA +∠MCD=90°. ∵OM ⊥AB ,∴∠OAC +∠ODA=90°. ∵OA=OC , ∴∠OAC=∠OCA , ∴∠MCD=∠ODA. 又∵∠ODA=∠MDC , ∴∠MCD=∠MDC , ∴MD=MC.(2)依题意可知AB=5×2=10,AC=4√5, ∵AB 为☉O 的直径,∴∠ACB=90°, ∴BC=√102-(4√5)2=2√5. ∵∠AOD=∠ACB ,∠A=∠A , ∴△AOD ∽△ACB , ∴OD BC=AO AC,即2√5=4√5,得OD=52.设MC=MD=x ,在Rt △OCM 中, 由勾股定理得x +522=x 2+52, 解得x=154,即MC=154.5.解:(1)证明:连接OD ,∵DE ∥OA ,∴∠AOC=∠OED ,∠AOD=∠ODE , ∵OD=OE ,∴∠OED=∠ODE , ∴∠AOC=∠AOD , 又∵OA=OA ,OD=OC ,∴△AOC ≌△AOD (SAS),∴∠ADO=∠ACO. ∵CE 是☉O 的直径,AC 为☉O 的切线, ∴OC ⊥AC ,∴∠OCA=90°, ∴∠ADO=∠OCA=90°,∴OD ⊥AB. ∵OD 为☉O 的半径, ∴AB 是☉O 的切线.(2)∵CE=6,∴OD=OC=3, ∵∠BDO=180°-∠ADO=90°, ∴BO 2=BD 2+OD 2, ∴OB=√42+32=5, ∴BC=8,∵∠BDO=∠OCA=90°,∠B=∠B , ∴△BDO ∽△BCA , ∴BD BC =ODAC , ∴48=3AC , ∴AC=6.6.解:(1)证明:连接OA ,∵∠B=60°,∴∠AOC=2∠B=120°,又∵OA=OC,∴∠OAC=∠OCA=30°,又∵AP=AC,∴∠P=∠ACP=30°,∴∠OAP=∠AOC-∠P=90°,∴OA⊥P A,∴P A是☉O的切线.(2)在Rt△OAP中,∵∠P=30°,∴PO=OD+PD=2OA,又∵OA=OD,∴PD=OA,∵PD=√5,∴CD=2OA=2PD=2√5.∴☉O的直径为2√5.7.解:(1)证明:∵AB是直径,∴∠ACB=90°,∵∠A=30°,∴AB=2BC.连接OC.AB,∵PC是☉O的切线,∴∠OCP=90°,∴∠BCP=∠P=30°,∴PB=BC,又∵BC=12∴P A=3PB.(2)∵点P在☉O外,PC是☉O的切线,C为切点,直线PO与☉O相交于点A,B,∴∠BCP=∠ACO=∠A,∵∠A+∠P+∠ACB+∠BCP=180°,且∠ACB=90°,∴2∠BCP=90°-∠P,(90°-∠P).∴∠BCP=128.解:(1)∵AF与☉O相切于点A,∴AF⊥OA,∵BD是☉O的直径,∴∠BAD=90°,∵∠BAC=120°,∴∠DAC=30°,∴∠DBC=∠DAC=30°,∵∠F=30°,∴∠F=∠DBC,∴AF∥BC,∴OA⊥BC,∴∠BOA=90°-30°=60°,∠AOB=30°.∴∠ADB=12(2)∵OA ⊥BC ,∴BE=CE=12BC=4,∴AB=AC ,∵∠AOB=60°,OA=OB ,∴△AOB 是等边三角形,∴AB=OB , ∵∠OBE=30°,∴OE=12OB ,BE=√3OE=4,∴OE=4√33,∴AC=AB=OB=2OE=8√33.。