当前位置：文档之家 › 切线的判定和性质

切线的判定和性质

  • 格式：ppt
  • 大小：374.00 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

切线的性质与判定

切线的性质与判定

P 图1切线的性质与判定直线与圆相切是直线与圆的特殊位置关系，有关的性质与判定也是圆中重点知识，现举例说明，供大家参考．一、切线性质的应用例1如图1，AB 是⊙O 的直径，PA 切⊙O 于A ，OP 交⊙O 于C ，连BC ．若∠P=30º，求∠B 的度数．分析：要求∠B 周角的2倍”，因此∠AOC=2∠B ，所以只要求出∠AOC 的度数，而PA 是⊙O 切线，根据圆的切线性质知△PAO 是直角三角形，而∠P 知，这样根据“直角三角形两锐角互余”即可求出∠B 的度数． 解：因为PA 切⊙O 于A ，AB 是⊙O 的直径，所以OA ⊥PA ，即∠PAO=90º．因为∠P=30º，所以∠AOC =90º－∠P=90º－30º=60º．又因为∠AOC=2∠B ，所以∠B=30º．点评：“圆的切线垂直于经过切点的半径”，这一性质在求角的度数和线段长度中有着广泛的应用．二、切线的判定例2（兴义）如图2，AB 是⊙O 的直径，点P 在BA ∠BPC=30°．求证：PC 是⊙O 的切线．分析：由于题目中没有明确直线PC 与⊙O 因为∠BPC=30°，所以OD=12OP ．因为AP=12AB AP=OA=12OP ．所以OD= OA ，即圆心O 到直线PC O 的切线．点评：圆的切线的判定常见方法有两种类型：一当已知条件中已明确给出直线与圆的公共点时，常采用连接这点和圆心这条辅助线，去证明这个半径垂直于已知直线．这种方法简称“连半径，证垂直”．二当已知条件中没有明确给出直线与圆的公共点时，常采用过圆心作直线的垂线段这条辅助线，去证明垂线段的长度等于圆的半径长．这种方法简称“作垂直，证半径”．本例属于第二种类型．。

2.3、 圆的切线的性质及判定定理

2.3、 圆的切线的性质及判定定理

即B一定点在圆外．由点B的任意性可知，圆与直线 只有一个公共点，因此l 是圆的切线．由此可得：
切线的判定定理：
经过半径的外端并且垂直于这 条半径的直线是圆的切线．
O
l
AB
例1 如图,AB是⊙O的直径, ⊙O过BC的中点D, DE⊥AC.求证:DE是⊙O是切线.
证明:连接OD.
∵BD=CD,OA=OB, ∴OD是△ABC的中位线,
D C
A
O
B
P322
思考:切线的性质定理逆命题“经过半径的外端并且 垂直于这条半径的直线是圆的切线．”是否成立?
已知：点A是⊙O与直线l 的公共点,且 l ⊥OA .
求证：圆与直线只有一个公共点 证明：在l 上任取异于点A的点B,则△OAB是Rt△
而OB是Rt△ OAB的斜边，因此，都有OB>OA,
C P321
∴OD//AC.
又∵∠DEC=90º ∴∠ODE=90º 又∵D在圆周上,
∴DE是⊙O是切线..E D NhomakorabeaB
A
O
三、 圆的切线的 性质及判定定理
O
r
l A MB
l
.O
1 切线的性质定理：圆的切线垂直于经过切点的半径．
l
AM
反证法
假设不垂直, 作OM⊥l
因“垂线段最 故OA>OM,
O
即短圆”心, 到直线距离小于半径.
这与线圆相切矛盾.
因为经过一点只有一条直线与已知直线垂直，所 以经过圆心垂直于切线的直线一定过切点；反之,过切 点且垂直于切线的直线也一定过圆心.由此得到：
推论1: 经过圆心且垂直于切线的直线必经过切点.
推论2: 经过切点且垂直于切线的直线必经过圆心.

圆的切线的性质及判定定理 课件

圆的切线的性质及判定定理 课件

【典例训练】
1.在Rt△ABC中，∠C=90°，AC=3 cB的关系为( )
(A)相切
(B)相离
(C)相交
(D)无法判断
2.如图所示，CB为⊙O的直径，P是CB的延
长线上一点，且OB=BP，∠AOC=120°，
则PA与⊙O的位置关系是_____.
圆的切线的性质
圆的切线的性质 (1)已知一条直线是圆的切线时,常作出过切点的半径,则该半 径垂直于切线,从而出现了直角. (2)从圆外一点引圆的两条切线,这点与圆心的连线平分这两条 切线的夹角,这点到切点的切线长相等. (3)连接圆的两条平行切线的切点的线段是圆的直径.
【典例训练】 1.如图所示，DB，DC是⊙O的两条切线，A是圆上一点，已知 ∠D=46°，则∠A=_____.
DO AD
AD
2.如图，已知EB是半圆O的直径，A是BE延长线上的一点，AC是 半圆O的切线，D为切点，BC⊥AC于C，若BC=6，AC=8，则 AE=_______.
【解析】1.如图所示，连接OB，OC，
则OB⊥BD，OC⊥CD，
则∠DBO+∠DCO=90°+90°=180°，
则四边形OBDC内接于一个圆，
则有∠BOC=180°-∠D=180°-46°=134°，
【解析】连接OC，∵OA=OB,AC=CB,OC=OC, ∴△OAC≌△OBC, ∴∠OCA=∠OCB=90°, ∴直线AB与⊙O相切. 答案：相切
1.圆的切线的其他相关性质 (1)切线和圆只有一个公共点; (2)切线和圆心的距离等于圆的半径; (3)过圆心且过切点的直线与过该点的切线垂直.
2.切线的判定定理 在切线的判定定理中要分清定理的题设和结论，“经过半径外 端”和“垂直于这条半径”这两个条件缺一不可，否则就不是 圆的切线，如图①②中的例子就不同时满足这两个条件，所以 都不是圆的切线.

切线的判定和性质

切线的判定和性质

切线的判定和性质
切线的性质与判定
1.主要性质
（1）切线和圆只有一个公共点；
（2）切线和圆心的距离等于圆的半径；
（3）切线垂直于经过切点的半径；
（4）经过圆心垂直于切线的直线必过切点；
（5）经过切点垂直于切线的直线必过圆心；
（6）从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

其中（1）是由切线的定义得到的，（2）是由直线和圆的位置关系定理得到的，（6）是由相似三角形推得的，也就是切割线定理。

2.判定
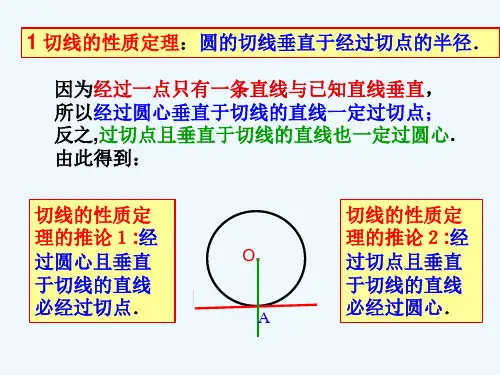
切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。

圆的切线垂直于这个圆过切点的半径。

中考真题;切线的判定与性质(答案详解)

中考真题;切线的判定与性质(答案详解)

中考复习：切线的判定与性质知识考点：1、掌握切线的判定及其性质的综合运用，在涉及切线问题时，常连结过切点的半径，切线的判定常用以下两种方法：一是连半径证垂直，二是作垂线证半径。

2、掌握切线长定理的灵活运用，掌握三角形和多边形的内切圆，三角形的内心。

精典例题：【例1】如图，AC 为⊙O 的直径，B 是⊙O 外一点，AB 交⊙O 于E 点，过E 点作⊙O 的切线，交BC 于D 点，DE ＝DC ，作EF ⊥AC 于F 点，交AD 于M 点。

（1）求证：BC 是⊙O 的切线；（2）EM ＝FM 。

：【例2】如图，△ABC 中，AB ＝AC ，O 是BC 的中点，以O 为圆心的圆与AB 相切于点D 。

求证：AC 是⊙O 的切线。

》【例3】如图，已知AB 是⊙O 的直径，BC 为⊙O 的切线，切点为B ，OC 平行于弦AD ，OA ＝r 。

<（1）求证：CD 是⊙O 的切线； （2）求OC AD ⋅的值；（3）若AD ＋OC ＝r 29，求CD 的长。

•例1图321MFOEDCB A例2图 EO D C B A •例3图321OD C BA探索与创新：【问题一】如图，以正方形ABCD 的边AB 为直径，在正方形内部作半圆，圆心为O ，CG 切半圆于E ，交AD 于F ，交BA 的延长线于G ，GA ＝8。

（1）求∠G 的余弦值；!（2）求AE 的长。

【问题二】如图，已知△ABC 中，AC ＝BC ，∠CAB ＝α（定值），⊙O 的圆心O 在AB 上，并分别与AC 、BC 相切于点P 、Q 。

,（1）求∠POQ ；（2）设D 是CA 延长线上的一个动点，DE 与⊙O 相切于点M ，点E 在CB 的延长线上，试判断∠DOE 的大小是否保持不变，并说明理由。

(|•问题一图 G F E O DCB A 问题二图NQ P EO DC BA答案精典例题：【例1】如图，AC 为⊙O 的直径，B 是⊙O 外一点，AB 交⊙O 于E 点，过E 点作⊙O 的切线，交BC 于D 点，DE ＝DC ，作EF ⊥AC 于F 点，交AD 于M 点。

圆切线的性质及判定

圆切线的性质及判定

圆切线的性质及判定一．切线的判定方法：⑴．切线的定义：与圆有唯一公共点的直线叫做圆的切线。

⑵．到圆心的距离等于半径的直线是圆的切线⑶．经过半径的外端，并且垂直于这条半径的直线是圆的切线。

二．辅助线规律：（1）直线与圆有公共点时，辅助线的作法是“连结圆心和公共点”，再证直线与半径垂直简称：“有点，连接，证垂直”。

即当条件中已知直线与圆有公共点时，利用“⑶．经过半径的外端，并且垂直于这条半径的直线是圆的切线”证明。

（2）当直线与圆并没明确有公共点时，辅助线的作法是“过圆心向直线作垂线”，再证圆心到直线的距离等于半径简称：“无点，作垂线，证（等于）半径”。

即当条件没有告诉直线与圆有公共点时，利用“（2）到圆心的距离等于半径的直线是圆的切线；”证明。

三．例题讲析：例1. 已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB求证：直线AB是⊙O的切线。

例2. 如图，已知OA=OB=5厘米，AB=8厘米，⊙O的直径为6厘米求证：AB与⊙O相切例3. 如图，已知AB是⊙O的直径，点D在AB的延长线上，BD=OB，点C在圆上，∠CAB=30°.求证：DC是⊙O的切线。

例4. 如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D.求证：AC平分∠DAB。

例5. 已知：AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于AD求证：DC是⊙O的切线。

例6. 如图，A是⊙O外一点，连OA交⊙O于C，过⊙O上一点P作OA的垂线交OA于F，交⊙O于E，连结PA，若∠FPC=∠CPA.求证：PA是⊙O的切线例7. 如图，AB=AC，以AB为直径的⊙O交BC于D，DE⊥AC于E求证：DE与⊙O相切例8. 如图，已知AB为⊙O的直径，BC切⊙O于B，AC交⊙O于P，CE=EB，E点在BC上。

求证：PE是⊙O的切线。

四．练习：1、如图7，AB为⊙O直径，PA、PC为⊙O的切线，A、C为切点，∠BAC=30°（1）求∠P大小。

初中数学切线的性质和判定


图29－3
线的性质和判定
解 析 (1)由切线的性质，即可得OA⊥PA，OB⊥PB，又由圆周角 定理，求得∠AOB的度数，继而求得∠APB的大小； (2)由切线长定理，可求得∠APO的度数，继而求得∠AOP的度数，易得 PO是AB的垂直平分线，然后利用三角函数的性质，求得AD与OD的长．
┃ 切线的性质和判定
切线的性质和判定
中考预测
如图 29－6，△ABC 内接于⊙O，∠B＝60°，
CD 是⊙O 的直径，点 P 是 CD 延长线上的一点，
且 AP＝AC.
(1)求证：PA 是⊙O 的切线；
(2)若 PD＝ 3，求⊙O 的直径．
图29－6
切线的性质和判定
解
(1)证明：连接 OA, ∵∠B＝60°，
∴∠AOC＝2∠B＝120°.
切线的性质和判定
[方法点析] 解三角形内切圆问题，主要是切线长定理的运 用．解决此类问题，常转化到直角三角形中，利用勾股定理或 直角三角形的性质及三角函数等解决．
┃ 切线的性质和判定
回归教材
切线问题中必需的半径
教材母题
如图 29－5，设 AB 是⊙O 的直径，如 果圆上点 D 恰使∠ADC＝∠B，那么直线 CD 与⊙O 相切吗？若相切，请给出证明．
∴S△AOB＝12×AB×OD＝12×10 3×5＝25 3(cm2)．
切线的性质和判定
[方法点析] (1)利用过圆外一点作圆的两条切线，这两条切 线的长相等，是解题的基本方法．(2)利用方程思想求切线长常 与勾股定理，切线长定理，圆的半径相等紧密相连．
切线的性质和判定
探究四 三角形的内切圆
命题角度： 1. 三角形的内切圆的定义； 2. 求三角形的内切圆的半径．

切线的判定与性质

E
56°
O
C F
B
2、如图,△ABC中,∠A的平分线 AD交BC于D,⊙O过点A,且和BC切 于D,和AB,AC分别交于E,F. 求证:EF∥BC A
1 2 O 4 D
E 3 B
F
C
O r
l
A
1、判断： (1)过半径的外端的直线是圆的切线（×） (2)与半径垂直的的直线是圆的切线（×）
(3)过半径的端点与半径垂直的直线是圆的 切线（×）
O l r A O r l O r l
A
A
判定直线与圆相切有哪些方法？
切线的判定方法有三种： •①直线与圆有唯一公共点； •②直线到圆心的距离等于该圆的半径； •③切线的判定定理．即 经过半径的外端并且垂直这条半径的 直线是圆的切线.
D
A E O C B
例1与例2的证法有何不同?
O A C B D A O B
E
C
(1)如果已知直线经过圆上一点,则连结这点和圆
心,得到辅助半径,再证所作半径与这直线垂直.
简记为：有交点，连半径,证垂直.
(2)如果已知条件中不知直线与圆是否有公共点,
则过圆心作直线的垂线段,再证垂线段长等于半
径长.简记为：无交点,作垂直,证半径.
C
A
B
∠CAB的顶点及两边与圆的 位置关系是什么？ C 顶点在圆 上，一边与圆 相交，另一边 与圆相切的角 叫做弦切角。 A B AC是弦切角∠CAB所夹的弧。
如图，说出图中所有的弦切角及其所夹 的弧。 弦切角∠CAD夹 ⌒ 的弧是AD B 弦切角∠CAB夹 的弧是ADB · E D O
弦切角∠CAE夹 的弧是ADE
点，则连接半径，应用
切线的பைடு நூலகம்质定理得到垂 直关系，从而应用勾股 定理计算。

数学人教版九年级上册圆的切线的性质及判定定理

根据作图,直线l是⊙O切线满足两个条件： O
l
A B
1.经过半径的外端； 2.与半径垂直．
应用格式(几何语言): OA是⊙O的半径 OA⊥l于A
l是⊙O的切线.
定理说明：在此定理中，题设是“经过半径的外端” 和“垂直于这条半径”，结论为“直线是圆的切 线”， 两个条件缺一不可，否则就不是圆的切线. 下面两个反例说明只满足其中一个条件的直线不是圆的切线：
O. O. A
l
l
A
B
３．应用： 例１ 如图，AB是⊙O的直径,⊙O过BC的中点D， DE⊥AC. 求证：DE是⊙O的切线．
证明：连接OD． ∵BD＝CD，OA=OB, ∴OD是△ABC的中位线. ∴OD//AC. 又∵ ∠DEC＝90°, ∴ ∠ODE＝90°. 又∵ D在圆周上, ∴ DE是⊙O的切线. C E D B A O
A O
C
D
B
练习3 若Rt△ABC内接于⊙O,∠A=30°. 延长斜边AB到D，使BD等于⊙O的半径, 求证：DC是⊙O的切线.
分析:如图
300 C 300 0 60 120.0 600 600 O B
A
D
O.
l
A
2. 如图,点A是⊙O与直线 l 的公共点,且 l ⊥OA .在直线 l 上任取异于点A的点B,则△OAB是 Rt△． 而OB是Rt△ OAB的斜边，因此，都有OB>OA,即B 一定点在圆外．由点B的任意性可知，圆与直线只有 一个公共点，因此 l 是圆的切线．由此可得： 切线的判定定理：经过半 径的外端并且垂直于这条 半径的直线是圆的切线．
C

B
练习1.如图A是⊙O外的一点，AO的延长线交 ⊙O于C，直线AB经过⊙O上一点B，且AB＝BC， ∠C＝30°. 求证：直线AB是⊙O的切线.

人教版数学第二十四章 第2节 切线的判定与性质

人教版数学第二十四章第2节切线的判定与性质一、内容和内容解析本节课的内容是人教版九年级数学下册《圆》这一章的第二节直线和圆的位置关系。

圆是几何学习中的重点难点，尤其是切线的相关知识是中考中的热点与难点。

切线的判定的教学在平面几何乃至整个中学数学教学中都占有重要地位和作用。

除了在证明和计算中有着广泛的应用外，它也是研究三角形内切圆的作法，切线长定理以及后面研究两圆的位置关系和正多边形与圆的关系的基础，所以它是《圆》这一章的重要内容，也可以说是本章的核心。

本节课的教学内容如下：一、切线的判定方法1.定义法：和圆只有一个公共点的直线是圆的切线，但是不常用。

2.数量法（距离法）：圆心到直线的距离等于半径的直线是圆的切线。

3.判定定理（最常用的方法）：经过半径的外端，并且垂直半径的直线是圆的切线，这是从位置关系进行判定。

其中使用判定定理时，两个条件缺一不可。

经过半径的外端垂直于这条半径的直线是圆的切线。

二、证明切线作辅助线的两种方法1.如果已知直线经过圆上一点，则连接这点和圆心得到辅助半径，再证所作半径与这条直线垂直。

简记：有公共点、连半径、证垂直。

2.如果已知条件中不知直线与圆是否有公共点，则过圆心作直线的垂线段为辅助线。

再证垂线段的长等于半径的长，即为有公共点、作垂直、证半径。

让学生在经历数学知识的探索和发现过程中，体验几何学习中推理的无穷乐趣，感受数学思维的严谨性和数学结论的确定性。

二、目标和目标解析按照课标要求，学生经历探索切线判定定理的过程，要能够灵活运用会运用切线的判定定理解决问题。

鉴于本节课是新授课，根据《数学课程标准》,数学教学必须建立在学生的认知发展水平和已有的知识经验基础之上，所以我确定了如下目标：1.知识与技能：①理解切线的判定定理，并能初步运用它解决简单的问题。

②知道判定切线的常用的三种方法，初步掌握方法的选择。

③掌握在解决切线的问题中常用的辅助线的作法。

2.过程与方法：①通过判定一条直线是否为圆的切线，训练学生的推理判断能力。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

情景导入
1、当你在下雨天快速转动雨伞时水飞出的方向 是什么方向？ 2、砂轮打磨零件飞出火星的方向是什么方向？
下雨天转动雨伞时飞出的水，以及在砂轮上打 磨工件飞出的火星，均沿着圆的切线的方向飞出。
自探1：
请在⊙O上任意取一点A，连接OA，
过点A作直线l⊥OA。思考：
（1）圆心O到直线l的距离和 圆的半径有什么数量关系?
∴ l ⊥OA
O
l A
总结:
切线的性质定理：圆的 切线垂直于过切点的半径。
O
l A
比较：
切线判定定理：
①过半径外端; ②垂直于这条半径.
切线性质定理：
①圆的切线; ②过切点的半径.
O
切线
l
A
切线垂直于半径
通过本节课的学习你还有什么疑问， 请大胆提出来，我们共同解决。
运用拓展：
1、判断：
(1)过半径的外端的直线是圆的切线（×） (2)与半径垂直的的直线是圆的切线（×）
O
A
B
C
分析：由于AB过⊙O上的点C，所以连接OC，
只要证明AB⊥OC即可。
例2 如图，已知：O为∠BAC平分线上一
点，OD⊥AB于D,以O为圆心，OD为半径作
⊙O。
求证：⊙O与AC相切。
A
B D
O
EC
自探2：
如图，如果直线l是⊙O的切线，切点为A， 那么半径OA与直线l是不是一定垂直呢？
∵ l是⊙O的切线，切点为A
辅助线作法：连接圆心与切点可得半径与切线垂直。即 “连半径，得垂直”。
经过圆的半径的外端且垂直于
这条半径的直线是圆的切线。
定理的几何语言表达：
O
∵ OA是半径， l ⊥OA于A
r
∴ l是⊙O的切线
l
A
对定理的理解： 切线必须同时满足两个条件：①经过
圆的半径的外端；②垂直于这条半径．
例1：如图，已知：直线AB经过⊙O上的点C，
并且OA=OB，CA=CB。
求证：直线AB是⊙O的切线。
米坪初中：冷任丽
复习回顾：
直线与圆的 位置关系
相交
相切Βιβλιοθήκη 相离图形公共点个数 公共点名称
直线名称 圆心到直线距
离d与半径r的
关系
Or
d
l
A
B
2个 交点
割线
d<r
Or d
l A
1个 切点 切线
d=r
Or d
l
没有
d>r
图中直线l满足什么条件时是⊙O的切线？
O 方法1：直线与圆有唯一公共点
l 方法2：直线到圆心的距离等于半径
(3)过半径的端点与半径垂直的直线是圆的
切线（×）
O l
r
A
O r
l
A
O l
r
A
2、如图,AB是⊙O的直径,点D在AB的延长线 上,BD=OB,点C在⊙O上, ∠CAB=30°.
求证:DC是⊙O的切线.
C
A OBD
3、如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O 的半径多少？
注：已知切线、切 点，则连接半径，应用 切线的性质定理得到垂 直关系，从而应用勾股 定理计算。
（2） 二者有什么位置关系？
为什么？
O
（3） 由此你发现了什么？ l
A
（先独立思考，解决不了的小组内讨论，时间5分钟。）
(1)直线l经过半径OA的外端点A；
(2)直线l垂直于半径0A．
则:直线l与⊙O相切
O l
A
这样我们就从“位置” 的角度得到了 圆的切线的判定方法——切线的判定定理．
切线的判定定理：
l是圆的切线 l是圆的切线 l是圆的切线
2、常用的做辅助线方法 ⑴直线与圆的公共点已知时，作出过公共点的半径，
再证半径垂直于该直线。（有交点、连半径，证垂直） ⑵直线与圆的公共点不确定时，过圆心作直线的垂线
段，再证明这条垂线段等于圆的半径。（无交点、作垂直， 证半径） 3、圆的切线性质定理：圆的切线垂直于经过切点的半径。
B OA P
4、如图，AB、AC分别切⊙O于B、C，若
∠A=600，点P是圆上异于B、C的一动点，则
∠BPC的度数是（ ）
A、600
B、1200
B
C、600或1200
O
D、1400或600 P
A
C
盘点收获的时刻到了！ 通过本节课的学习，你有 什么收获？
1、判定切线的方法
直线l
与圆有唯一公共点 与圆心的距离等于圆的半径 经过半径外端且垂直这条半径