湖北宜昌市第一中学2015届高三下学期第二次模拟考试数学(理)试卷 Word版含答案

2 侧视图俯视图第4题图2015届高三第二次联考 数学试题（理科）一、选择题：本大题共10小题，每小题5分，共50分．在每个小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集为R ，集合{}{}221,320x A x B x x x =≥=-+≤，则R A C B = A. {}0x x ≤ B. {}1x x≤≤2 C. {}012x x x ≤<>或D. {}012x x x ≤<≥或2. 若复数z 满足(1)42(z i i i +=-为虚数单位），则||z =3. 执行如图所示的程序框图，则输出S 的值为C. 0D. 4. 某几何体的三视图（单位：cm ）如右图所示，其中侧视图是一个边长为 2的正三角形，则这个几何体的体积是A. 32cm 3cm C. 333cm D. 33cm 5. 在等腰ABC ∆中，90,2,2,BAC AB AC BC BD ∠====3AC AE =，则AD BE ⋅的值为A ．43-B ．13-C ．13D ．436. 设不等式组0x y x y y ⎧+≤⎪⎪-≥⎨⎪≥⎪⎩M ，函数y =x 轴所围成的区域为N ,向M 内随机投一个点,则该点落在N 内的概率为 A. 2π B. 4π C.8π D. 16π7. 下列说法正确的是A. “0x <”是“ln(1)0x +<”的充要条件B. “2x ∀≥，2320x x -+≥”的否定．．是“2,x ∃<2320x x -+<” C. 采用系统抽样法从某班按学号抽取5名同学参加活动，学号为5,16,27,38,49的同学均被选出，则该班学生人数可能为60 D. 在某项测量中，测量结果X 服从正态分布2(1,)(0)N σσ>，若X 在(0,1)内取值的概率为0.4，则X 在(0,2)内取值的概率为0.88. 已知抛物线C ：28y x =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点，若3FP FQ =，则||QF =A.83 B. 52C. 3D. 2 9. 已知函数213,10()132,01x g x x x x x ⎧- -<≤⎪=+⎨⎪-+<≤⎩，若方程()0g x mx m --=有且仅有两个不等的第3题图实根，则实数m 的取值范围是A ．9(,2][0,2]4-- B ．11(,2][0,2]4-- C ．9(,2][0,2)4-- D ．11(,2][0,2)4--10.函数()y f x =图像上不同两点1122(,),(,)A x y B x y 处的切线的斜率分别是,A B k k ，规定||(,)||A B k k A B AB ϕ-=叫做曲线()y f x =在点A 与点B 之间的“弯曲度”，给出以下命题：①函数321y x x =-+图像上两点A 与B 的横坐标分别为1,2，则(,)A B ϕ> ②存在这样的函数，图像上任意两点之间的“弯曲度”为常数； ③设点A 、B 是抛物线21y x =+上不同的两点，则(,)2A B ϕ≤；④设曲线xy e =上不同两点1122(,),(,)A x y B x y ，且121x x -=，若(,)1t A B ϕ⋅<恒成立，则实数t 的取值范围是(,1)-∞.以上正确命题的序号为 A. ①② B. ②③ C. ③④ D. ②③④二、填空题：本大题共6个小题，考生共需作答5小题，每小题5分，共25分．请将答案填在答题卡对应题号．．．．．．．的位置上．答错位置，书写不清，模棱两可均不得分． （一） 必考题（11—14题） 11. 已知二项式21()nx x+的展开式的二项式系数之和为32，则展开式中含x 项的系数是_ _.12. 若实数,,a b c 满足232a b c ++=，则当22223a b c ++取最小值时，249a b c ++的值为________.13. 如图，在平面直角坐标系xoy 中，将直线2x y =与直线1x =及x 轴所围成的图形绕x 轴旋转一周得到一个圆锥，圆锥的体积120()2xV dx =⎰π圆锥310.1212x ==ππ据此类比：将曲线2(0)y x x =≥与直线2y =及y 轴所围成的图形绕y 轴旋转一周得到一个旋转体，该旋转体的体积______V =.14.设数列{}n a 共有n 项*(3,)n n N ≥∈,且11n a a ==，对于每个*(11,)i i n n N ≤≤-∈均有11{,1,3}3i i a a +∈. （1）当3n =时，满足条件的所有数列{}n a 的个数为__________；13（2）当10n =时，满足条件的所有数列{}n a 的个数为_________.(二) 选考题（请考生在第15、16两题中任选一题做答，请先在答题卡指定位置将你所选的题目序号所在方框用2B 铅笔涂黑．如果全选，则按第15题作答结果计分．）15. （选修4—1：几何证明选讲）如图，PA 与圆O 相切于A ，不过圆心O 的割线PCB 与直径AE 相交于D 点.已知∠BPA =30，2=AD ，1=PC ,则圆O 的半径等于__________． 16. （选修4—4：坐标系与参数方程）已知直线l 的参数方程为132x ty t =+⎧⎨=-⎩（t 为参数），以坐标原点为极点, x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为22sin()4πρθ=+，则直线l 与曲线C 相交的弦长为__________．三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤． 17.（本小题满分12分）已知函数()cos cos()3f x x x π=+.(Ⅰ)求()f x 的最小正周期；(Ⅱ)在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，若1(),4f C =-2,a =且ABC ∆的面积为23，求边长c 的值.18. （本小题满分12分）等差数列{}n a 的前n 项和为n S ，数列{}n b 是等比数列，满足113,1a b ==，2252310,2.b S a b a +=-=(Ⅰ)求数列{}n a 和{}n b 的通项公式；(Ⅱ)令设数列{}n c 的前n 项和n T ，求2.n T19. （本小题满分12分）端午节即将到来，为了做好端午节商场促销活动，某商场打算将进行促销活动的礼品盒重新设计.方案如下：将一块边长为10的正方形纸片ABCD 剪去四个全等的等腰三角形,,,,SEE SFF SGG SHH ''''∆∆∆∆再将剩下的阴影部分折成一个四棱锥形状的包装盒S EFGH -,其中,,,A B C D 重合于点O ，E 与E '重合，F 与F '重合，G 与G '重合，H 与H '重合（如图所示）. （Ⅰ）求证：平面SEG ⊥平面SFH ；（Ⅱ）当52AE =时,求二面角E SH F --的余 弦值.20.（本小题满分12分）根据最新修订的《环境空气质量标准》指出空气质量指数在050，各类人群可正常活动．某市环保局在2014年对该市进行了为期一年的空气质量检测，n 为奇数，n 为偶数，2,,n n n S c b ⎧⎪=⎨⎪⎩第20题图A HG ′ D S G BEHOGF第19题图S· ′H ′O PA CDE第15题图·得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为[)0,10，[)10,20，[)20,30，[)30,40，[]40,50，由此得到样本的空气质量指数频率分布直方图，如图．（Ⅰ）求a 的值；并根据样本数据，试估计这一年度的空气质量指数的平均值；（Ⅱ）用这50个样本数据来估计全年的总体数据，将频率视为概率．如果空气质量指数不超过20，就认定空气质量为“最优等级”．从这一年的监测数据中随机抽取2天的数值，其中达到“最优等级”的天数为ξ，求ξ的分布列，并估计一个月（30天）中空气质量能达到“最优等级”的天数．21. （本小题满分13分）如图，已知椭圆22221(0),(2,0)x y a b A a b+=>>是长轴的一个端点，弦BC 过椭圆的中心O ，且0,2AC BC OC OB BC BA ⋅=-=-.（Ⅰ）求椭圆的方程；（Ⅱ）设P 、Q 为椭圆上异于,A B 且不重合的两点，且PCQ ∠的平分线总是垂直于x 轴，是否存在实数λ，使得PQ AB =λ，若存在，请求出λ最大值，若不存在，请说明理由.22. （本小题满分14分）已知函数221()ln ,(),,2f x x mxg x mx x m R =-=+∈令()()()F x f x g x =+.（Ⅰ）当12m =时，求函数()f x 的单调递增区间； （Ⅱ）若关于x 的不等式()1F x mx ≤-恒成立，求整数．．m 的最小值； （Ⅲ）若2m =-，正实数12,x x 满足1212()()0F x F x x x ++=，证明：12x x +≥湖北省 八校 2015届高三第二次联考数学试题（理科）参考答案1-5 CDABA 6-10 BDACB11. 10 12. 5 13. 2π 14. （1）3 （2）3139 15. 7 16.1. 解析：{|0},{|12},{|12}R A x x B x x C B x x x =≥=≤≤=<>或，∴R A C B ={}012x x x ≤<>或2. 解析：42(42)(1)13,||1(1)(1)i i i z i z i i i ---===-=++-第21题图鄂南高中 黄冈中学 黄石二中 华师一附中 襄阳四中 襄阳五中 孝感高中 荆州中学3.解析：289sinsinsinsin 3333S ππππ=++++= 4. 解析：由图知几何体的体积为11(12)232V =⋅+⋅= 5. 解析：11(),23AD AB AC BE AE AB AC AB =+=-=-2211114()()().23233AD BE AB AC AC AB AC AB ∴⋅=+⋅-=-=- 6. 解析：区域M 的面积为2，区域N 的面积为2π，由几何概型知所求概率为4P π=. 7. 解析：A 中应为必要不充分条件；B 中命题的否定为“2x ∃≥，2320x x -+≥”；C 错；D 对.8. 解析：设l 与x 轴的交点为M ，过Q 向准线l 作垂线，垂足为N ，则由23NQ MF =及4MF p ==可得8.3QF =9. 解析：令()0g x mx m --=得()(1)g x m x =+，原方程有两个相异的实根等价于两函数()y g x =与(1)y m x =+的图象有两个不同的交点.当0m >时，易知临界位置为(1)y m x =+过点(0,2)和(1,0)，分别求出这两个位置的斜率12k =和20k =，由图可知此时[0,2)m ∈当0m <时，设过点(1,0)-向函数1()3,(1,0]1g x x x =-∈-+的图象作切线的切点为00(,)x y ，则由函数的导数为21()(1)g x x '=-+得020001(1)1131y x x y x ⎧-=⎪++⎪⎨⎪=-⎪+⎩解得001332x y ⎧=-⎪⎪⎨⎪=-⎪⎩，得切线的斜率为194k =-，而过点(1,0),(0,2)--的斜率为12k =-，由图知此时9(,2]4m ∈--，9(,2][0,2)4m ∴∈--10.解析：①错：(1,1),(2,5),|||7,(,)A B A B ABk k A B ϕ=-=∴=< ②对：如1y =；③对：(,)2A B ϕ==≤；④错：1212(,)x x x x A B ϕ==，12111,(,)(,)t A B A B ϕϕ==><恒成立，故1t ≤. 11.解析：由232n=得5n =，251031551()rrrr rr T C xC xx --+⎛⎫==⎪⎝⎭，令1031r -=得3r =，故含x 项的系数为3510C =．12.解析：由柯西不等式得22222224(23)[))](1)ab c a =++≤++++2224223.63a b c ∴++≥=此时,1a a b c ==∴==又232a b c ++=，1,24953a b c a b c ∴===∴++=13.解析：22222001|2.2V dy ydy y ππππ====⎰⎰14.解析：（1）当3=n 时，因为211,1,33a a ⎧⎫∈⎨⎬⎩⎭，321,1,33a a ⎧⎫∈⎨⎬⎩⎭， 所以21,1,33a ⎧⎫∈⎨⎬⎩⎭，211,1,33a ⎧⎫∈⎨⎬⎩⎭，所以213a =或12=a 或23a =所以满足条件的所有数列{}n a 的个数为3个； (2)令1(19)i i ia b i a +=≤≤，则对每个符合条件的数列{}n a 满足条件 31010212912911a a a a b b b a a a a ⋅⋅⋅=⋅⋅⋅⋅==，且1,1,33i b ⎧⎫∈⎨⎬⎩⎭反之符合上述条件的9项数列{}n b ，可唯一确定一个符合条件的10项数列{}n a 记符合条件的数列{}n b 的个数为N ， 显然(19)i b i ≤≤中有k 个3，k 个13，92k -个1 当k 给定时，{}n b 的取法有99kkk C C -种，易得k 的可能值为0,1,2,3,4, 故112233449897969513139.N C C C C C C C C =++++=所以满足条件的所有数列{}n a 的个数为3139个.15.解析：Rt PAD ∆中，2,4,AD PD PA =∴==由切割线定理得2,PA PC PB =⋅21,PB ∴=⋅12,8PB BD ∴=∴=又由相交弦定理得,AD ED CD BD ⋅=⋅12,ED ∴=所以直径为14，故半径为7.16.解析：把直线l 的参数方程化为普通方程得25x y +=，把曲线C 的极坐标方程化为普通方程得22(1)(1)2x y -+-===17.解析：21()cos (cos cossin sin )cos 2332f x x x x x x ππ==11cos(2)234x π=++…………………4分（1）T π=； …………………6分 （2）111()cos(2),cos(2)1,.234433f C C C C πππ=++=-∴+=-∴= …………………8分 13sin 23,8,2,4,24ABCSab Cab ab a b ===∴==∴= …………………10分 由余弦定理得2222cos 12,c a b ab C c =+-=∴= …………………12分 18.解析：(Ⅰ)设数列{}n a 的公差为d ，数列{}n b 的公比为q ，则 由2252310,2,b S a b a +=⎧⎨-=⎩得610,34232,q d d q d ++=⎧⎨+-=+⎩解得2,2,d q =⎧⎨=⎩所以32(1)21n a n n =+-=+，12n n b -=． …………………4分 (Ⅱ)由13a =，21n a n =+得(2)n S n n =+，则即 …………………6分21321242()()n n n T c c c c c c -=+++++++32111111[(1)()()](222)3352121n n n -=-+-++-++++-+ …………………9分12(14)12114nn -=-++-22(41)213n n n =+-+ …………………12分 19.解：（Ⅰ）折后,,,A B C D 重合于一点,O ∴拼接成底面EFGH 的四个直角三角形必为全等的等腰直角三角形，∴底面EFGH 是正方形，故EG FH ⊥. …………………2分在原平面图形中，等腰三角形SEE SGG ''∆∆,,SE SG ∴=.EG SO ∴⊥ ………………4分又,,,SO FH SFH SO FH O ⊂⋂=EG ∴⊥平面SFH .又EG ⊂平面SEG ，∴平面SEG ⊥平面SFH . …………………6分n 为奇数， n 为偶数， 12,(2)2,n n n n c -⎧⎪+=⎨⎪⎩111,22,n n c n n -⎧-⎪=+⎨⎪⎩n 为奇数， n 为偶数，（Ⅱ）法1：过O 作OM SH ⊥交SH 于M 点，连EM ,EO ⊥面SFH ,EO SH ∴⊥, SH ∴⊥面EMO ，EMO ∴∠为二面角E SH F --的平面角. …………………8分 当52AE =时，即5,2OE =Rt SHO中，5,SO OH SO SH OM SH⋅==∴==Rt EMO中，EM ==,2cos .3OM EMO EM ∠=== 所以所求二面角的余弦值为2.3…………………12分 法2：由（Ⅰ）知,,EG FH EG SO ⊥⊥并可同理得到,HF SO ⊥故以O 为原点，分别以,,OF OG OS 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系O xyz - 在原平面图形中，5,2AE =则底面正方形EFGH 的对角线5EG =，555555(,0,0),(0,,0),(0,,0),(,,0),(0,,0).222222H E G HE OG ∴--=-=在原平面图形中，可求得SE 在Rt SO E ∆中，可求得5,SO =5(0,0,5),(,0,5),2S SH ∴=-- …………………8分设平面SEH 的一个法向量为(,,)n x y z =，则550,2550,22n SH x z n HE x y ⎧⋅=--=⎪⎪⎨⎪⋅=-=⎪⎩得,12y x z x =⎧⎪⎨=-⎪⎩ 令2x =，则(2,2,1)n =- …………………10分EG ⊥平面SFH ，OG ∴是平面SFH 的一个法向量，设二面角E SH F --的大小为,θ则2cos .3n OGn OG θ-==⋅∴二面角E SH F --的余弦值为2,3 …………………12分20.解：(Ⅰ)由题意，得(0.030.0320.010.008)101,a ++++⨯=解得0.02.a =…………………3分 50个样本中空气质量指数的平均值为0.150.2150.32250.3350.084525.6X =⨯+⨯+⨯+⨯+⨯=由样本估计总体，可估计2014年这一年度空气质量指数的平均值约为25.6 …………6分 （Ⅱ）利用样本估计总体，该年度空气质量指数在[]0,20内为“最优等级”，且指数达到“最优等级”的概率为0.3，则(2,0.3)B ξ.ξ的可能取值为0，1，2，0021224942(0)(0.3)(0.7),(1)(0.3)(0.7),100100P C P C ξξ==⨯===⨯=2229(2)(0.3)100P C ξ===ξ∴的分布列为：…………………8分 494290120.6100100100E ξ=⨯+⨯+⨯=.(或者20.30.6E ξ=⨯=)， …………………10分 故一个月（30天）中空气质量能达到“最优等级”的天数大约为300.618⨯=天. … 12分 21.解：（I ）∵0,AC BC ⋅= ∴,90AC BC ACB ⊥∠=︒又2,OC OB BC BA -=-即2BC AC =，∴△AOC 是等腰直角三角形 ……………2分 ∵(2,0),A ∴(1,1)C 而点C 在椭圆上，∴22111,2,a a b +== ∴243b =∴所求椭圆方程为223144x y += …………………4分（II ）对于椭圆上两点P 、Q ，∵∠PCQ 的平分线总是垂直于x 轴∴PC 与CQ 所在直线关于1x =对称，设(0PC k k k =≠且1)k ≠±，则CQ k k =-，………6分 则PC 的直线方程1(1)(1)1y k x y k x -=-⇒=-+ ① QC 的直线方1(1)(1)1y k x y k x -=--⇒--+ ②将①代入223144x y +=得222(13)6(1)3610k x k k x k k +--+--= ③∵(1,1)C 在椭圆上，∴1x =是方程③的一个根，∴22361113p p k k x x k --⋅==+ ……………8分以k -替换k ，得到2236131Q k k x k +-=+.222226242()211313121231313p Q p Q PQp Q p Q k k k k y y k x x k k k k k k x x x x k k--⋅--+-++=====----++而1,3AB k =∴,PQ AB k k = ∴PQ ∥AB ，∴存在实数λ，使得PQ AB =λ ………………10分||(PQ x ===当2219k k =时即21,3k k ==时取等号，又||10AB =maxλ==…………………… 13分 22.解：⑴21(),0,2f x lnx x x =->211()(0)x f x x x x x-'=-=> ……………………2分由()0,f x '>得210,x ->又0,x >所以01x <<．所以()f x 的单增区间为(0,1). ………4分（2）方法一：令21()()(1)(1)1,2G x F x mx lnx mx m x =--=-+-+所以21(1)1()(1)mx m x G x mx m x x-+-+'=-+-=．当0m ≤时，因为0x >，所以()0G x '>．所以()G x 在(0,)+∞上是递增函数，又因为213(1)11(1)120,22G ln m m m =-⨯+-+=-+>所以关于x 的不等式()1G x mx ≤-不能恒成立． ………………………6分 当0m >时，21()(1)(1)1()m x x mx m x m G x xx-+-+-+'==-． 令()0,G x '=得1x m =，所以当1(0,)x m ∈时，()0;G x '>当1(,)x m∈+∞时，()0G x '<． 因此函数()G x 在1(0,)x m ∈是增函数，在1(,)x m∈+∞是减函数． 故函数()G x 的最大值为2111111()()(1)1ln .22G ln m m m m m m m m =-⨯+-⨯+=- …………8分令1()ln ,2h m m m =-因为11(1)0,(2)20,24h h ln =>=-< 又因为()h m 在(0,)m ∈+∞上是减函数，所以当2m ≥时，()0h m <． 所以整数m 的最小值为2． ……………10分方法二：⑵由()1F x mx ≤-恒成立，得2112lnx mx x mx -+≤-在(0,)+∞上恒成立．问题等价于2112lnx x m x x ++≥+在(0,)+∞上恒成立．令21()12lnx x h x x x ++=+，只要max ()m h x ≥． ……………………6分因为221(1)()2(),1()2x x lnx h x x x +--'=+令()0,h x '=得102x lnx --=．设1()2x x lnx ϕ=--，因为11()02x x ϕ'=--<，所以()x ϕ在(0,)+∞上单调递减，不妨设102x lnx --=的根为0x ．当0(0,)x x ∈时，()0;h x '>当0(,)x x ∈+∞时，()0h x '<．所以()h x 在0(0,)x x ∈上是增函数；在0(,)x x ∈+∞上是减函数．所以000max020*********()()11(1)22x lnx x h x h x x x x x x +++====++． …………………8分因为111()20,(1)0242ln ϕϕ=->=-< 所以01 1.2x <<此时max 0112,()(1,2).g x x <<∈所以2,m ≥即整数m 的最小值为2 …… 10分 （3）当2m =-时，2(),0F x lnx x x x =++>由1212()()0,F x F x x x ++=即22111222120lnx x x lnx x x x x ++++++=从而212121212()()()x x x x x x ln x x +++=⋅-⋅ ……………………13分令12,t x x =⋅则由()ln t t t ϕ=-得，1()t t tϕ-'= 可知()t ϕ'在区间（0，1）上单调递减，在区间(1,)+∞上单调递增。

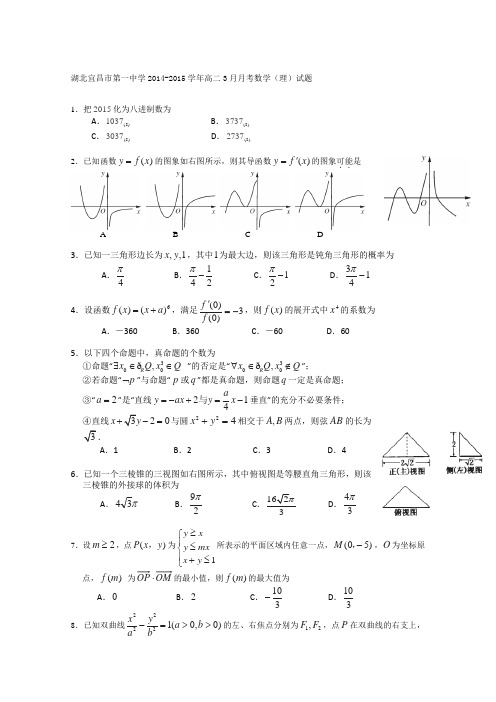
湖北宜昌市第一中学2014-2015学年高二3月月考数学（理）试题1．把2015化为八进制数为A ．(8)1037B ．(8)3737C ．(8)3037D ．(8)27372．已知函数()y f x =的图象如右图所示，则其导函数()y f x '=的图象可能．．是A B C D3．已知一三角形边长为,,1x y ，其中1为最大边，则该三角形是钝角三角形的概率为A ．4πB ．142π-C ．12π-D ．314π-4．设函数6()()f x x a =+，满足3)0()0(-='f f ，则)(x f 的展开式中4x 的系数为 A ．－360 B ．360 C ．－60 D ．605．以下四个命题中，真命题的个数为①命题“300,R x Q x Q ∃∈∈ð ”的否定是“300,R x Q x Q ∀∈∉ð”；②若命题“p ⌝”与命题“p 或q ”都是真命题，则命题q 一定是真命题；③“2a =”是“直线214ay ax y x =-+=-与垂直”的充分不必要条件； ④直线320x +-=与圆224x y +=相交于,A B 两点，则弦AB 3A ．1B ．2C ．3D ．46．已知一个三棱锥的三视图如右图所示，其中俯视图是等腰直角三角形，则该三棱锥的外接球的体积为A ．π34B ．92π C 162π D ．43π7．设2m ≥，点)(y x P ，为1y xy mx x y ≥⎧⎪≤⎨⎪+≤⎩所表示的平面区域内任意一点，)50(-，M ，O 为坐标原点，)(m f 为OM OP ⋅的最小值，则)(m f 的最大值为A ．0B ．2C ．310- D ．1038．已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为12,F F ，点P 在双曲线的右支上，且12||4||PF PF =，则此双曲线的离心率e 的值不可能．．．为 A ．53 B ．2 C ．43 D ．549．正四棱锥S ABCD -中，侧棱与底面所成角为α，侧面与底面所成二面角为β，侧棱SB 与底面正方形ABCD 的对角线AC 所成角为γ，相邻两侧面所成二面角为θ， 则,,,αβγθ之间的大小关系是A ．αβθγ＜＜＜B ． αβγθ＜＜＜C ．αγβθ＜＜＜D ．βαγθ＜＜＜10．设()e (0)ax f x a =>．过点(,0)P a 且平行于y 轴的直线与曲线:()C y f x =的交点为Q ，曲线C 过点Q 的切线交x 轴于点R ，则PQR ∆的面积的最小值是A ．1BC ．e2D ．2e 4二、填空题：本大题共5小题，共25分．请将答案填在答题卡对应题号的位置上．答错位置，书写不清，模棱两可均不得分．11．某校高一高二田径队有运动员98人，其中高一有56人．按用分层抽样的方法，从全体运动员中抽出一个容量为28的样本，那么应抽取高二运动员人数是 ．12．若)(x f 在R 上可导，3)2('2)(2++=x f x x f ，则(1)f = ．13．如图，,A B 是O 上的两点，且OA OB ⊥，2OA =，C 为OA 中点，连接BC 并延长交O 于点D ，则CD = ．14．三对夫妻排成一排照相，仅有一对夫妻相邻的排法种数为 ．15．若抛物线24y x =的内接ABC ∆的重心恰为其焦点F ，则⑵111AB BC CAk k k ++= ．三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤．16．（本小题满分12分）设命题p ：实数x 满足x 2－4ax ＋3a 2<0，其中a >0，命题q ：实数x 满足2ln(28)ln(32)x x x +--…．(1)若a ＝1，且p ∧q 为真，求实数x 的取值范围；(2)若p 是q 的必要不充分条件，求实数a 的取值范围．17．（本小题满分12分）为增强市民节能环保意识，某市面向全市征召义务宣传志愿者．现从符合条件的500名志愿者中随机抽取100名志愿者，他们的年龄情况如下表所示． （Ⅰ）频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图（如图），再根据频率分布直方图估计这500名志愿者中年龄在[30，35)岁的人数； （Ⅱ）在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加中心广场的宣传活动，从这20人中选取2名志愿者担任主要负责人，记这2名志愿者中“年龄低于30岁”的人数为X ，求X 的分布列及数学期望．18．（本小题满分12分）已知函数1()ln (1)f x x a x=--,a ∈R ． (Ⅰ)求()f x 的单调区间； (Ⅱ)若()f x 的最小值为0，求实数a 的值．19．（本小题满分12分）如图1，在Rt △ABC 中，∠ACB =30°，∠ABC =90°，D 为AC 中点，AE BD ⊥ 于E ，延长AE 交BC 于F ，将∆ABD 沿BD 折起，使平面ABD ⊥平面BCD ，如图2所示. （Ⅰ）求二面角A –DC –B 的余弦值． （Ⅱ）在线段AF 上是否存在点M 使得EM 平面ADC ？若存在,请指明点M 的位置；若不存在，请说明理由．BF1图 图 220．（本小题满分13分）已知F 为椭圆22:143x y C +=的右焦点，椭圆C 上的任意一点P 到点F 的距离与P 到直线:l x m =的距离之比为12．(Ⅰ)求直线l 的方程； (Ⅱ)设A 为椭圆C 的左顶点，过点F 的直线与椭圆C 交于D E 、两点，直线AD AE 、与l 交于点M N 、．以MN 为直径的圆是否过定点？若是，求出定点坐标；若不是，说明理由．21．（本小题满分14分）牛顿在《流数法》一书中，给出了一种求方程近似解的数值方法——牛顿法．它的具体步骤是： ①对于给定方程()0f x =，考查其对应函数()y f x =（左图中较粗曲线），在曲线上取一个初始点00(,())x f x ；②作出过该点曲线的切线0l ，0l 与x 轴的交点横坐标记为1x ； ③用1x 替代0x 再作出切线1l ，重复以上过程得到2x ． 一直继续下去，得到数列01,,,n x x x ，它们越来越接近方程的真实解λ．（其中()0i f x '≠，0,1,2,,i n =）如果给定一个精确度0μ()0f x =的近似解．其算法程序框图为右图：请回答以下问题： (Ⅰ)写出框图中横线处用0x 表示1x 的关系式；(Ⅱ)若2()1f x x =-，02x =，00.2μ=，则该程序运行的结果为多少？ (Ⅲ)在(Ⅱ)条件下（精确度不计），证明所得12,,,n x x x 满足使数列1lg 1n n x x ⎧⎫+⎨⎬-⎩⎭为等比数列，且1213n x x x n +++-<．根据频率分布直方图估计这500名志愿者中年龄在[30，35)的人数为500×0.35＝175．……4分（Ⅱ）用分层抽样的方法，从中选取20人，则其中“年龄低于30岁”的有5人，“年龄不低于30岁”的有15人．………………………………………6分由题意知，X的可能取值为0，1，2，P(X＝0)＝C215C220＝2138，P(X＝1)＝C15C115C220＝1538，P(X＝2)＝C25C220＝238＝119． (10)=2EX……………………12分令()1ln (0)g x x x x =-+>，则11()1xg x x x-'=-+=， 由()0g x '>，解得01x <<；由()0g x '<，解得1x >．所以()g x 的单调递增区间为(0,1)，单调递减区间为(1,)+∞． 故max [()](1)0g x g ==，即当且仅当1x =时，()0g x =.因此，1a =． …………………………………………………………………………………………12分19. 解：（Ⅰ）因为平面ABD ⊥平面BCD ，交线为BD ，又在ABD ∆中，AE BD ⊥于E ，AE ⊂平面ABD所以AE ⊥平面BCD . …………………………………………………………………2分 由题意可知EF BD ⊥，又AE ⊥BD .如图，以E 为坐标原点，分别以,,EF ED EA 所在直线为x 轴， y 轴，z 轴， 建立空间直角坐标系E xyz - 不妨设2AB BD DC AD ====，则1BE ED ==. 由图1条件计算得，AE =BC =，EF =则(0,0,0),(0,1,0),(0,1,0),,0,0),E D B A F C -(3,1,0),(0,1,DC AD ==.由AE ⊥平面BCD 可知平面DCB 的法向量为EA . 设平面ADC 的法向量为(,,)x y z =n ，则0,0.DC AD ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0.y y +==⎪⎩ ……………………………………………………………4分令1z =，则1y x ==，所以(1,3,1)=-n . 平面DCB 的法向量为EA ，所以cos ,||||EA EA EA ⋅<>==-⋅n n n所以二面角A DC B -- …………………………………………………6分 （Ⅱ）设AMAF λ=，其中[0,1]λ∈.由于3(AF =， 所以(AM AF λλ==，其中[0,1]λ∈所以3,0,(1EM EA AM λ⎛=+=-……………………………………………10分由0EM ⋅=n 0λ=-(1- 解得3=(0,1)4λ∈.所以在线段AF 上存在点M 使EM ADC ∥平面，且34AM AF =. ………………………12分方法二：（Ⅰ）由题意ABD ∆为正三角形，且E 为BD 的中点，不妨设2AB BD DC AD ====,则1BE ED ==，由AE BCD ⊥面，过E 作CD 的延长线的垂线于H ，连AH ，可知AH CD ⊥，AHE ∴∠为二面角A DCB --的平面角， ……………………………………3分sin 60,EH DE AE AH ==∴=o ,cos EH AHE AH ∴∠== 故二面角A DC B --. ………………………………………………………………6分 （Ⅱ）取AB 中点为G ，BC 中点为N ，连接,,EG GN EN ，GN 交AF 于M ，不难得：//EGN ADC 平面平面，则//EM ADC 平面，M 为所求， (8)分设AM AF λ=,BA a BC b ==，，F 为BC 上靠近B 点的一个三等分点，1()23GM AM AG a b λλ=-=-+，1122GN BN BG a b =-=-+//GN GM 1113()6224AM AF λλλ∴-=-⇒==所以在线段AF 上存在点M 使EM ADC ∥平面，且34AM AF = . ………………………12分21. 解：(I)由已知，0l 的方程为000()()()y f x f x x x '-=⋅-，令0y =得0100()()f x x x f x =-'； …2分 (II) 2()1f x x =-，()2f x x '=，故22000100000()11()22f x x x x x x f x x x -+=-=-='， …………3分当02x =时，154x =，此时52340.228μ-==>，进行循环， 当054x =时，14140x =，此时41594040.25504μ-==<，故输出14140x =； ………5分(III)由(II)，数列{}n x 满足154x =且2112n n n x x x ++=，22212221111212(1)1112(1)12n n n n n n n n n n n nx x x x x x x x x x x x ++++++++∴===+-+---， ……………………………… 7分故21211(1)1lg lg 2lg 1(1)1n n n n n n x x x x x x +++++==⋅---，而111lg lg 901x x +=≠-， ∴1lg 1n n x x ⎧⎫+⎨⎬-⎩⎭为以lg 9为首项，2为公比的等比数列． ……………………………… 9分11lg2lg 92lg 31n n n n x x -+∴=⋅=⋅-，得223131nnn x +=-， ……………………………… 10分方法一：（与等比数列比较） 考查22131nn x -=-，比较231n-与1810n -⨯的大小，当1n =时，20318810-==⨯，当2n …时，由于221n n --…，23n =或时取等222222212318118080108010nn n n n -----∴-=-⨯⨯厖 （其中等号均在2n =时取得）． 故11222111()81041031nn n n x ---==⋅⨯-… ……………………………… 12分1212111111111441041011(1)11051410 .149183110n n n n x x x n x x x -∴+++-=-+-++-+⨯++⋅-=<⨯=<-………………14分 方法二：（裂项求和） 当2n …时，由1222222231(31)(31)31n n n n -----=+⋅->+得111111212222222222(31)(31)1111131(31)(31)31313131n n nn n n n n n n x --------+---===-<--+⋅--+++， ………12分1121112122244224881622211111111111()()()()3131313131313131111111111111()[()()()]248108082313131313131231231.8080331n n n n n n n x x x n x x x -----∴+++-=-+-++-=-+-+-++--+-+-+-+<-+-++-+-+-++-++++++=-<<+………… 14分。

高中数学学习材料鼎尚图文*整理制作宜昌市第一中学2015届高三年级适应性考试（二）数 学（文史类）本试卷共4页，共22题。

全卷满分150分，考试时间120分钟。

★祝考试顺利★注意事项：1. 答卷前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。

2. 选择题的作答，每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3. 填空题和解答题的作答：用签字笔直接写在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4.考试结束后，请将答题卡上交。

一、选择题：每小题5分，10小题共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、i 为虚数单位，复数11i-的虚部是（ ） A.12- B ．12 C ．1i 2- D . 1i 22、甲：函数()f x 是R 上的单调递增函数；乙：121212,,,()()x x R x x f x f x ∃∈<<，则甲是乙的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 3、要得到一个偶函数，只需将()sin 2f x x =的图象（ ）A ．向右平移2π个单位 B ．向右平移4π个单位C ．向左平移2π个单位 D ．向左平移π个单位4、某电影院统计电影放映场次的情况如右图所示．下列函数模型中，最不合适近似描述电影放映场次逐年变化规 律的是（ ）A ．2y ax bx c =++B ．xy ae b =+C ．b ax y +=3D ．ln y a x b =+5、如右图,在△ABC 中, 14AN NC =uuu r uuu r ,P 是BN 上的一点,若16AP m AB AC −−→−−→−−→=+,则实数m的值为（ ）A.16 B.13 C.1 D.36、执行如图所示的程序框图，输出结果S=（ ）A.2015B.2016C. -2015D.-20167、已知点(,)P x y 的坐标满足条件11350x y x x y ≥⎧⎪≥-⎨⎪+-≤⎩，那么点P 到直线34130x y --=的距离的最小值为（ ）A.95 B.115C.1D.2 8、设min{, }p q 表示p ，q 两者中的较小者，若函数2()min{3, log }f x x x =-，则满足1()2f x £的x 的集合为 （ ）A ．(]50,2+2，轹÷ê去÷÷êøë B ．522轾犏犏臌， C ．(50, 2,2轹ù÷ê+?÷ú÷ûêøëU D ．()502+2，，骣÷ç去÷ç÷ç桫 9、已知,,O A B 三地在同一水平面内，A 地在O 地正东方向2km 处，B 地在O 地正北方向 2km 处，某测绘队员在,A B 之间的直线公路上任选一点C 作为测绘点，用测绘仪进行测绘，O 地为一磁场，距离其不超过3km 的范围内会对测绘仪等电子仪器形成干扰，使 测量结果不准确，则该测绘队员能够得到准确数据的概率是（ ）A.12 B.22C.212-D.312- 10、已知F 为双曲线22221(0,0)x y a b a b-=>>的右焦点，A 为双曲线虚轴的一个顶点，过点F 、A 的直线与双曲线的一条渐近线在y 轴右侧的交点为B ，若(21)A B A F u u r u ur =-，则此双曲线的离心率是（ ）A ．2B ．3C ．22D ．5二、填空题：本大题共7个小题，每小题5分，共35分。

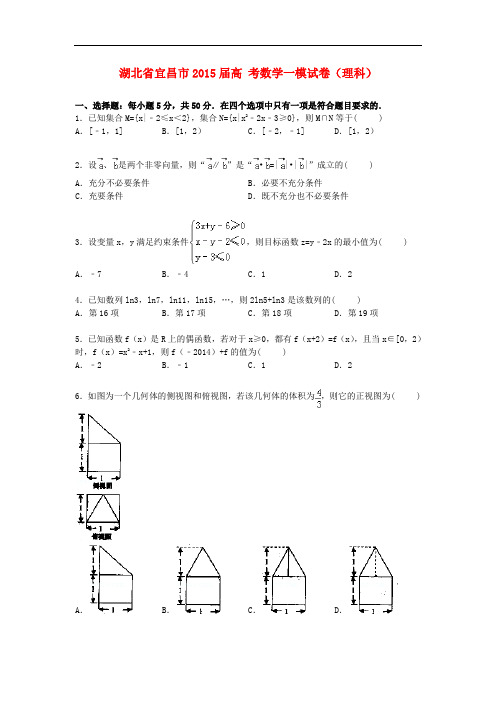
湖北省宜昌市2015届高考数学一模试卷（理科）一、选择题：每小题5分，共50分．在四个选项中只有一项是符合题目要求的．1．已知集合M={x|﹣2≤x＜2}，集合N={x|x2﹣2x﹣3≥0}，则M∩N等于( )A．[﹣1，1] B．[1，2）C．[﹣2，﹣1] D．[1，2）2．设、是两个非零向量，则“∥”是“•=||•||”成立的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3．设变量x，y满足约束条件，则目标函数z=y﹣2x的最小值为( ) A．﹣7 B．﹣4 C．1 D．24．已知数列ln3，ln7，ln11，ln15，…，则2ln5+ln3是该数列的( )A．第16项B．第17项C．第18项D．第19项5．已知函数f（x）是R上的偶函数，若对于x≥0，都有f（x+2）=f（x），且当x∈[0，2）时，f（x）=x2﹣x+1，则f（﹣2014）+f的值为( )A．﹣2 B．﹣1 C．1 D．26．如图为一个几何体的侧视图和俯视图，若该几何体的体积为，则它的正视图为( )A．B．C．D．7．在△ABC中，内角A，B，C的对边分别为a，b，c，且b2+c2+bc﹣a2=0，则=( )A．﹣B．C．﹣D．8．如图，面积为8的平行四边形OABC，对角线AC⊥CO，AC与BO交于点E，某指数函数y=a x （a＞0，且a≠1），经过点E，B，则a=( )A．B．C．2 D．39．设F1、F2是双曲线﹣=1（a＞0，b＞0）的左、右焦点，A是其右支上一点，连接AF1交双曲线的左支于点B，若|AB|=|AF2|，且∠BAF2=60°，则该双曲线的离心率为( ) A．B．C．2﹣1 D．10．由无理数引发的数学危机已知延续带19世纪，直到1872年，德国数学家戴德金提出了“戴德金分割”，才结束了持续2000多年的数学史上的第一次大危机．所谓戴金德分割，是指将有理数集Q划分为两个非空的子集M与N，且满足M∪N=Q，M∩N=∅，M中的每一个元素都小于N中的每一个元素，则称（M，N）为戴金德分割．试判断，对于任一戴金德分割（M，N），下列选项中不可能恒成立的是( )A．M没有最大元素，N有一个最小元素B．M没有最大元素，N也没有最小元素C．M有一个最大元素，N有一个最小元素D．M有一个最大元素，N没有最小元素二、填空题：考生只需作答5小题，每小题5分，共25分．11．已知平面向量=（1，2），=（1，k2﹣1），若⊥，则k=__________．12．已知x+2y+3z=2，则x2+y2+z2的最小值是__________．13．如图，一桥拱的形状为抛物线，该抛物线拱的高为h=6m，宽为b=24m，则该抛物线拱的面积为__________m2．14．若以曲线y=f（x）上任意一点M（x1，y1）为切点作切线l1，曲线上总存在异于M的点N（x2，y2），以点N为切点做切线L2，且l1∥l2，则称曲线y=f（x）具有“可平行性”，现有下列命题：①偶函数的图象都具有“可平行性”；②函数y=sinx的图象具有“可平行性”；③三次函数f（x）=x3﹣x2+ax+b具有“可平行性”，且对应的两切点M（x1，y1），N（x2，y2）的横坐标满足x1+x2=；④要使得分段函数f（x）=的图象具有“可平行性”，当且仅当实数m=1．其中的真命题是__________（写出所有命题的序号）．一、选考题：只选一题作答．（选修4-1：几何证明选讲）15．如图，已知图中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=，AF=2BF．若CE与圆相切，且CE=，则BE=__________．一、选修4-4：坐标系参数方程16．在平面直角坐标系中，曲线C的方程为（θ为参数），在以此坐标系的原点为极点，x轴的正半轴为极轴的极坐标系中，直线l的极坐标方程为ρsin（θ+）=1，则直线l与曲线C的公共点共有__________个．三、解答题：共75分．解答应写出必要的文字说明、证明过程或演算步骤．17．已知函数f（x）=1+2sinxcosx﹣2sin2x，x∈R．（1）求函数f（x）的单调增区间；（2）在△ABC中，a，b，c分别是角A，B，C的对边，已知a=3，b=，f（A）=1，求角C．18．等差数列{a n}的前n项和为S n，已知a1=7，a2为整数，当且仅当n=4时，S n取得最大值．（1）求数列{a n}的通项公式；（2）设b n=（9﹣a n）•2n﹣1，求数列{b n}的前n项和为T n．19．某单位有员工1000名，平均每人每年创造利润10万元．为了增加企业竞争力，决定优化产业结构，调整出x（x∈N*）名员工从事第三产业，调整后他们平均每人每年创造利润为万元（a＞0），剩下的员工平均每人每年创造的利润可以提高0.2x%．（1）若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润，则最多调整出多少名员工从事第三产业？（2）在（1）的条件下，若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润，则a的取值范围是多少？20．如图，三棱柱ABC﹣A1B2C3的底面是边长为4正三角形，AA1⊥平面ABC，AA1=2，M为A1B1的中点．（Ⅰ）求证：MC⊥AB；（Ⅱ）在棱CC1上是否存在点P，使得MC⊥平面ABP？若存在，确定点P的位置；若不存在，说明理由．（Ⅲ）若点P为CC1的中点，求二面角B﹣AP﹣C的余弦值．21．在平面直角坐标系xOy中，已知曲线C1上的任意一点到点A（﹣1，0），B（1，0）的距离之和为2．（Ⅰ）求曲线C1的方程；（Ⅱ）设椭圆C2：x2+=1，若斜率为k的直线OM交椭圆C2于点M，垂直于OM的直线ON交曲线C1于点N．（i）求证：|MN|的最小值为；（ii）问：是否存在以原点为圆心且与直线MN相切的圆？若存在，求出圆的方程；若不存在，请说明理由．22．已知函数f（x）=lnx+．（1）求曲线y=f（x）在（2，f（2））处的切线方程；（2）若g（x）=f（x）﹣+ax2﹣2x有两个不同的极值点．其极小值为M，试比较2M与﹣3的大小，并说明理由；（3）设q＞p＞2，求证：当x∈（p，q）时，＞．湖北省宜昌市2015届高考数学一模试卷（理科）一、选择题：每小题5分，共50分．在四个选项中只有一项是符合题目要求的．1．已知集合M={x|﹣2≤x＜2}，集合N={x|x2﹣2x﹣3≥0}，则M∩N等于( ) A．[﹣1，1] B．[1，2）C．[﹣2，﹣1] D．[1，2）考点：交集及其运算．专题：集合．分析：求出N中不等式的解集确定出N，找出M与N的交集即可．解答：解：由N中不等式变形得：（x﹣3）（x+1）≥0，解得：x≤﹣1或x≥3，即N=（﹣∞，﹣1]∪[3，+∞），∵M=[﹣2，2），∴M∩N=[﹣2，﹣1]，故选：C．点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．设、是两个非零向量，则“∥”是“•=||•||”成立的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：根据向量数量积的意义以及充分条件和必要条件的定义进行判断即可．解答：解：若•=||•||cos＜，＞=||•||，即cos＜，＞=1，故＜，＞=0，即∥且方向相同，即必要性成立，若＜，＞=π，满足∥但•=||•||cos＜，＞=﹣||•||，即充分性不成立，故“∥”是“•=||•||”成立的必要不充分条件，故选：B．点评：本题主要考查充分条件和必要条件的判断，根据向量数量积与向量夹角之间的关系是解决本题的关键．3．设变量x，y满足约束条件，则目标函数z=y﹣2x的最小值为( ) A．﹣7 B．﹣4 C．1 D．2考点：简单线性规划．专题：不等式的解法及应用．分析：先根据条件画出可行域，设z=y﹣2x，再利用几何意义求最值，将最小值转化为y轴上的截距最小，只需求出直线z=y﹣2x，过可行域内的点B（5，3）时的最小值，从而得到z最小值即可．解答：解：设变量x、y满足约束条件，在坐标系中画出可行域三角形，平移直线y﹣2x=0经过点A（5，3）时，y﹣2x最小，最小值为：﹣7，则目标函数z=y﹣2x的最小值为﹣7．故选A．点评：借助于平面区域特性，用几何方法处理代数问题，体现了数形结合思想、化归思想．线性规划中的最优解，通常是利用平移直线法确定．4．已知数列ln3，ln7，ln11，ln15，…，则2ln5+ln3是该数列的( ) A．第16项B．第17项C．第18项D．第19项考点：数列的概念及简单表示法．专题：等差数列与等比数列．分析：由数列3，7，11，15，…，可知此数列的通项公式可得a n=3+4（n﹣1）=4n﹣1．令2ln5+ln3=ln（4n﹣1），解出即可．解答：解：由数列3，7，11，15，…，可知此数列的通项公式可得a n=3+4（n﹣1）=4n﹣1．令2ln5+ln3=ln（4n﹣1），∴75=4n﹣1，解得n=19．∴2ln5+l n3是该数列的第19选．故选：D．点评：本题考查了等差数列的通项公式、对数的运算性质，考查了计算能力，属于基础题．5．已知函数f（x）是R上的偶函数，若对于x≥0，都有f（x+2）=f（x），且当x∈[0，2）时，f（x）=x2﹣x+1，则f（﹣2014）+f的值为( )A．﹣2 B．﹣1 C．1 D．2考点：函数奇偶性的性质．专题：计算题；函数的性质及应用．分析：对f，运用f（x+2）=f（x），即为f（1），对于f（﹣2014），先由偶函数的定义，再由f（x+2）=f（x），可得f（0），再由当x∈[0，2）时，f（x）=x2﹣x+1，计算即可得到．解答：解：若对于x≥0，都有f（x+2）=f（x），则f=f（2×1007+1）=f（1），由于函数f（x）是R上的偶函数，则f（﹣x）=f（x），即有f（﹣2014）=f=f（2×1007）=f（0），当x∈[0，2）时，f（x）=x2﹣x+1，则f（0）=1，f（1）=1，即有f（﹣2014）+f=2．故选D．点评：本题考查函数的奇偶性和周期性的运用：求函数值，考查运算能力，属于基础题．6．如图为一个几何体的侧视图和俯视图，若该几何体的体积为，则它的正视图为( )A．B．C．D．考点：简单空间图形的三视图．专题：探究型；空间位置关系与距离．分析：由几何体的侧视图和俯视图，可知几何体为组合体，上方为棱锥，下方为正方体，棱锥顶点在底面上的射影为正方形一边上的中点，由此可得结论．解答：解：由几何体的侧视图和俯视图，可知几何体为组合体，上方为棱锥，下方为正方体由俯视图可得，棱锥顶点在底面上的射影为正方形一边上的中点，顶点到正方体上底面的距离为1由此可知B满足条件故选B．点评：本题考查三视图，考查学生的空间想象能力，属于基础题．7．在△ABC中，内角A，B，C的对边分别为a，b，c，且b2+c2+bc﹣a2=0，则=( )A．﹣B．C．﹣D．考点：余弦定理；正弦定理．分析：由b2+c2+bc﹣a2=0，利用余弦定理可得cosA==﹣，A=120°．再利用正弦定理可得==，化简即可得出．解答：解：∵b2+c2+bc﹣a2=0，∴cosA==﹣，∴A=120°．由正弦定理可得====．故选：B．点评：本题考查了正弦定理与余弦定理的应用、两角和差的正弦余弦公式，考查了推理能力与计算能力，属于中档题．8．如图，面积为8的平行四边形OABC，对角线AC⊥CO，AC与BO交于点E，某指数函数y=a x （a＞0，且a≠1），经过点E，B，则a=( )A．B．C．2 D．3考点：指数函数的图像与性质．专题：函数的性质及应用．分析：首先设点E（t，a t），则点B坐标为（2t，2a t），又因为2a t=a2t，所以a t=2；然后根据平行四边形的面积是8，求出t的值，代入a t=2，求出a的值即可．解答：解：设点E（t，a t），则点B坐标为（2t，2a t），又因为2a t=a2t，所以a t=2；因为平行四边形OABC的面积=OC×AC=a t×2t=4t，又平行四边形OABC的面积为8所以4t=8，t=2，所以．故选：A．点评：本题主要考查了指数函数的图象和性质，属于基础题．9．设F1、F2是双曲线﹣=1（a＞0，b＞0）的左、右焦点，A是其右支上一点，连接AF1交双曲线的左支于点B，若|AB|=|AF2|，且∠BAF2=60°，则该双曲线的离心率为( ) A．B．C．2﹣1 D．考点：双曲线的简单性质．专题：计算题；解三角形；圆锥曲线的定义、性质与方程．分析：由题意可得△BAF2为等边三角形，设AF2=t，则AB=BF2=t，再由双曲线的定义，求得t=4a，再由余弦定理可得a，c的关系，结合离心率公式即可计算得到．解答：解：若|AB|=|AF2|，且∠BAF2=60°，则△BAF2为等边三角形，设AF2=t，则AB=BF2=t，由双曲线的定义可得，AF1﹣AF2=2a，BF2﹣BF1=2a，AF1=AB+BF1，即有t+2a=2t﹣2a，解得，t=4a，AF1=6a，AF2=4a，F1F2=2c，由余弦定理可得，F1F22=AF12+AF22﹣2AF1•AF2cos60°，即有4c2=36a2+16a2﹣2×6a×4a×，即为4c2=28a2，则有e==．故选D．点评：本题考查双曲线的离心率的求法，考查双曲线的定义的运用，考查余弦定理的运用，考查运算能力，属于中档题．10．由无理数引发的数学危机已知延续带19世纪，直到1872年，德国数学家戴德金提出了“戴德金分割”，才结束了持续2000多年的数学史上的第一次大危机．所谓戴金德分割，是指将有理数集Q划分为两个非空的子集M与N，且满足M∪N=Q，M∩N=∅，M中的每一个元素都小于N中的每一个元素，则称（M，N）为戴金德分割．试判断，对于任一戴金德分割（M，N），下列选项中不可能恒成立的是( )A．M没有最大元素，N有一个最小元素B．M没有最大元素，N也没有最小元素C．M有一个最大元素，N有一个最小元素D．M有一个最大元素，N没有最小元素考点：子集与真子集．专题：计算题；集合．分析：由题意依次举例对四个命题判断，从而确定答案．解答：解：若M={x∈Q|x＜0}，N={x∈Q|x≥0}；则M没有最大元素，N有一个最小元素0；故A正确；若M={x∈Q|x＜}，N={x∈Q|x≥}；则M没有最大元素，N也没有最小元素；故B正确；若M={x∈Q|x≤0}，N={x∈Q|x＞0}；M有一个最大元素，N没有最小元素，故D正确；M有一个最大元素，N有一个最小元素不可能，故C不正确；故选C．点评：本题考查了学生对新定义的接受与应用能力，属于基础题．二、填空题：考生只需作答5小题，每小题5分，共25分．11．已知平面向量=（1，2），=（1，k2﹣1），若⊥，则k=．考点：平面向量数量积的运算．专题：计算题；平面向量及应用．分析：运用向量垂直的条件：数量积为0，由数量积的坐标表示，解方程即可得到k．解答：解：平面向量=（1，2），=（1，k2﹣1），若⊥，则=0，即1+2（k2﹣1）=0，解得，k=．故答案为：．点评：本题考查平面向量垂直的条件：数量积为0，考查运算能力，属于基础题．12．已知x+2y+3z=2，则x2+y2+z2的最小值是．考点：二维形式的柯西不等式．专题：不等式的解法及应用．分析：由条件利用柯西不等式（12+22+32）（x2+y2+z2）≥（x+2y+3z）2，求得x2+y2+z2的最小值．解答：解：12+22+32=14，∴由柯西不等式可得（12+22+32）（x2+y2+z2）≥（x+2y+3z）2=4，∴x2+y2+z2≥=，即x2+y2+z2的最小值是，故答案为：．点评：本题主要考查了函数的最值，以及柯西不等式的应用，解题的关键是利用柯西不等式（12+22+32）（x2+y2+z2）≥（x+2y+3z）2，进行解决．13．如图，一桥拱的形状为抛物线，该抛物线拱的高为h=6m，宽为b=24m，则该抛物线拱的面积为96m2．考点：抛物线的应用．专题：圆锥曲线的定义、性质与方程．分析：建立坐标系，设抛物线方程为x2=﹣2py（p＞0），则将（12，﹣6）代入可得p=12，y=﹣，该抛物线拱的面积为2（12×6﹣），即可得出结论．解答：解：由题意，建立如图所示的坐标系，设抛物线方程为x2=﹣2py（p＞0），则将（12，﹣6）代入可得p=12，∴y=﹣，∴该抛物线拱的面积为2（12×6﹣）=2（72﹣24）=96m2，故答案为：96．点评：解决该试题的关键是利用定积分表示出抛物线拱的面积，然后借助于定积分得到结论．14．若以曲线y=f（x）上任意一点M（x1，y1）为切点作切线l1，曲线上总存在异于M的点N（x2，y2），以点N为切点做切线L2，且l1∥l2，则称曲线y=f（x）具有“可平行性”，现有下列命题：①偶函数的图象都具有“可平行性”；②函数y=sinx的图象具有“可平行性”；③三次函数f（x）=x3﹣x2+ax+b具有“可平行性”，且对应的两切点M（x1，y1），N（x2，y2）的横坐标满足x1+x2=；④要使得分段函数f（x）=的图象具有“可平行性”，当且仅当实数m=1．其中的真命题是②④（写出所有命题的序号）．考点：利用导数研究曲线上某点切线方程．专题：导数的综合应用．分析：分别求出函数导数，根据导数的几何意义求出对应的切线斜率，结合曲线y=f（x）具有“可平行性”，即可得到结论．解答：解：①函数y=1满足是偶函数，函数的导数y′=0恒成立，此时，任意两点的切线都是重合的，故①不符号题意．②由y′=cosx和三角函数的周期性知，cosx=a（﹣1≤a≤1）的解有无穷多个，符合题意．③三次函数f（x）=x3﹣x2+ax+b，则f′（x）=3x2﹣2x+a，方程3x2﹣2x+a﹣m=0在判别式△=（﹣2）2﹣12（a﹣m）≤0时不满足方程y′=a（a是导数值）至少有两个根．命题③错误；④函数y=e x﹣1（x＜0），y′=e x∈（0，1），函数y=x+，y′=1﹣，则由1﹣∈（0，1），得∈（0，1），∴x＞1，则m=1．故要使得分段函数f（x）的图象具有“可平行性”，当且仅当实数m=1，④正确．∴正确的命题是②④．故答案为：②④点评：本题考查了导数的几何意义，关键是将定义正确转化为：曲线上至少存在两个不同的点，对应的导数值相等，综合性较强，考查了转化思想．一、选考题：只选一题作答．（选修4-1：几何证明选讲）15．如图，已知图中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=，AF=2BF．若CE与圆相切，且CE=，则BE=．考点：与圆有关的比例线段．专题：立体几何．分析：由相交弦定理得DF•FC=AF•BF，由此解得AF=2，BF=1，AB=3，由切割线定理得CE2=BE•AE，由此能求出BE的长．解答：解：∵两条弦AB与CD相交于点F，E是AB延长线上一点，∴DF•FC=AF•BF，∵DF=CF=，AF=2BF，∴2BF2=2，解得AF=2，BF=1，AB=3，∵CE与圆相切，且CE=，∴CE2=BE•AE，∴（）2=BE（3+BE），解得BE=，或BE=﹣（舍）．故答案为：．点评：本题考查与圆有关的线段长的求法，是中档题，解题时要注意相交弦定理和切割线定理的合理运用．一、选修4-4：坐标系参数方程16．在平面直角坐标系中，曲线C的方程为（θ为参数），在以此坐标系的原点为极点，x轴的正半轴为极轴的极坐标系中，直线l的极坐标方程为ρsin（θ+）=1，则直线l与曲线C的公共点共有1个．考点：参数方程化成普通方程；简单曲线的极坐标方程．专题：直线与圆．分析：由曲线C的方程（θ为参数），消去参数化为x2+y2=1，可得圆心C，半径r．由直线l的极坐标方程ρsin（θ+）=1，展开为=1，化为y+x﹣=0．再利用点到直线的距离公式可得圆心到直线l的距离d，再与半径r比较大小即可．解答：解：由曲线C的方程（θ为参数），消去参数化为x2+y2=1，可得圆心C （0，0），半径r=1．由直线l的极坐标方程ρsin（θ+）=1，展开为=1，化为y+x﹣=0．∴圆心C到直线l的距离d==1=r．因此直线l与⊙C相切，有且只有一个公共点．故答案为：1．点评：本题考查了把极坐标方程化为直角坐标方程、参数方程化为普通方程、直线与曲线的交点判断、点到直线的距离公式，考查了推理能力与计算能力，属于基础题．三、解答题：共75分．解答应写出必要的文字说明、证明过程或演算步骤．17．已知函数f（x）=1+2sinxcosx﹣2sin2x，x∈R．（1）求函数f（x）的单调增区间；（2）在△ABC中，a，b，c分别是角A，B，C的对边，已知a=3，b=，f（A）=1，求角C．考点：正弦定理；正弦函数的图象．专题：计算题；三角函数的求值；三角函数的图像与性质；解三角形．分析：（1）运用二倍角公式和两角和的正弦公式，以及正弦函数的单调增区间，解不等式即可得到所求区间；（2）由特殊角的三角函数值，求出A，再由正弦定理，求得B，再由三角形的内角和定理，可得C．解答：解：（1）f（x）=1+2sinxcosx﹣2sin2x=sin2x+cos2x=2sin（2x+），令2kπ﹣≤2x+≤2kπ+，k∈Z，解得kπ﹣≤x≤kπ+，则函数的单调增区间为[kπ﹣，kπ+]，k∈Z；（2）f（A）=1，即为2sin（2A+）=1，即sin（2A+）=，由于A为三角形的内角，则2A+=，即A=，由正弦定理得sinB===，由于a＞b，则A＞B，则B=，则C=π﹣﹣=．点评：本题考查三角函数的化简和求值，考查正弦函数的单调区间，考查正弦定理及运用，考查运算能力，属于中档题．18．等差数列{a n}的前n项和为S n，已知a1=7，a2为整数，当且仅当n=4时，S n取得最大值．（1）求数列{a n}的通项公式；（2）设b n=（9﹣a n）•2n﹣1，求数列{b n}的前n项和为T n．考点：数列的求和；等差数列的性质．专题：等差数列与等比数列．分析：（1）设等差数列{a n}的公差为d，由于当且仅当n=4时，S n取得最大值．可得a4＞0，a5＜0．解得，由于a2为整数，可得d为整数，即可得出．（2）b n=（9﹣a n）•2n﹣1=n•2n．利用“错位相减法”、等比数列的前n选和公式即可得出．解答：解：（1）设等差数列{a n}的公差为d，∵当且仅当n=4时，S n取得最大值．∴a4＞0，a5＜0．∴，解得，∵a2为整数，∴d为整数，∴d=﹣2．∴a n=7+（n﹣1）×（﹣2）=9﹣2n．（2）b n=（9﹣a n）•2n﹣1=2n•2n﹣1=n•2n．∴T n=1×2+2×22+3×23+…+n•2n，2T n=22+2×23+3×24+…+（n﹣1）×2n+n×2n+1，∴﹣T n=2+22+23+…+2n﹣n•2n+1=﹣n×2n+1=（1﹣n）×2n+1﹣2，∴T n=（n﹣1）×2n+1+2．点评：本题考查了等差数列的通项公式及其性质、“错位相减法”、等比数列的前n选和公式，考查了推理能力与计算能力，属于中档题．19．某单位有员工1000名，平均每人每年创造利润10万元．为了增加企业竞争力，决定优化产业结构，调整出x（x∈N*）名员工从事第三产业，调整后他们平均每人每年创造利润为万元（a＞0），剩下的员工平均每人每年创造的利润可以提高0.2x%．（1）若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润，则最多调整出多少名员工从事第三产业？（2）在（1）的条件下，若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润，则a的取值范围是多少？考点：基本不等式在最值问题中的应用；函数模型的选择与应用．专题：计算题；应用题．分析：（1）根据题意可列出10（1000﹣x）（1+0.2x%）≥10×1000，进而解不等式求得x的范围，确定问题的答案．（2）根据题意分别表示出从事第三产业的员工创造的年总利润和从事原来产业的员工的年总利润，进而根据题意建立不等式，根据均值不等式求得求a的范围．解答：解：（1）由题意得：10（1000﹣x）（1+0.2x%）≥10×1000，即x2﹣500x≤0，又x＞0，所以0＜x≤500．即最多调整500名员工从事第三产业．（2）从事第三产业的员工创造的年总利润为万元，从事原来产业的员工的年总利润为万元，则（1+0.2x%）所以，所以ax≤，即a≤恒成立，因为，当且仅当，即x=500时等号成立．所以a≤5，又a＞0，所以0＜a≤5，即a的取值范围为（0，5]．点评：本题主要考查了基本不等式在求最值问题中的应用．考查了学生综合运用所学知识，解决实际问题的能力．20．如图，三棱柱ABC﹣A1B2C3的底面是边长为4正三角形，AA1⊥平面ABC，AA1=2，M为A1B1的中点．（Ⅰ）求证：MC⊥AB；（Ⅱ）在棱CC1上是否存在点P，使得MC⊥平面ABP？若存在，确定点P的位置；若不存在，说明理由．（Ⅲ）若点P为CC1的中点，求二面角B﹣AP﹣C的余弦值．考点：与二面角有关的立体几何综合题；直线与平面垂直的判定．专题：综合题；空间位置关系与距离；空间角．分析：（Ⅰ）取AB中点O，连接OM，OC，证明AB⊥平面OMC，可得MC⊥AB；（Ⅱ）建立空间直角坐标系，设P（0，2，t）（0≤t≤2），要使直线MC⊥平面ABP，只要•=0，•=0，即可得出结论；（Ⅲ）若点P为CC1的中点，求出平面PAC的一个法向量、平面PAB的一个法向量，利用向量的夹角公式，即可求二面角B﹣AP﹣C的余弦值．解答：（I）证明：取AB中点O，连接OM，OC．∵M为A1B1中点，∴MO∥A1A，又A1A⊥平面ABC，∴MO⊥平面ABC，∴MO⊥AB∵△ABC为正三角形，∴AB⊥CO又MO∩CO=O，∴AB⊥平面OMC又∵MC⊂平面OMC∴AB⊥MC（II）解：以O为原点，建立空间直角坐标系．如图．依题意O（0，0，0），A（﹣2，0，0）B（2，0，0），C（0，2，0），M（0，0，2）．设P（0，2，t）（0≤t≤2），则=（0，2，﹣2），=（4，0，0），=（0，2，t）．要使直线MC⊥平面ABP，只要•=0，•=0，即12﹣2t=0，解得t=．∴P的坐标为（0，2，）．∴当P为线段CC1的中点时，MC⊥平面ABP（Ⅲ）解：取线段AC的中点D，则D（﹣1，，0），易知DB⊥平面A1ACC1，故=（3，﹣，0）为平面PAC的一个法向量．…．又由（II）知=（0，2，﹣2）为平面PAB的一个法向量．设二面角B﹣AP﹣C的平面角为α，则cosα=||=．∴二面角B﹣AP﹣C 的余弦值为．点评：本小题主要考查空间直线与直线、直线与平面的位置关系、二面角等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查数形结合思想、化归与转化思想、函数与方程思想．21．在平面直角坐标系xOy中，已知曲线C1上的任意一点到点A（﹣1，0），B（1，0）的距离之和为2．（Ⅰ）求曲线C1的方程；（Ⅱ）设椭圆C2：x2+=1，若斜率为k的直线OM交椭圆C2于点M，垂直于OM的直线ON交曲线C1于点N．（i）求证：|MN|的最小值为；（ii）问：是否存在以原点为圆心且与直线MN相切的圆？若存在，求出圆的方程；若不存在，请说明理由．考点：直线与圆锥曲线的综合问题．专题：圆锥曲线中的最值与范围问题．分析：（Ⅰ）由椭圆定义可知曲线C1的轨迹是椭圆，设C1的方程为，由已知条件知2a=2，c=1，由此能求出曲线的方程．（Ⅱ）（ⅰ）当k=0，M为C2长轴端点，N为C1短轴的端点，|MN|=设直线OM：y=kx，代入x2+=1，得（2+3k）x2=2，由此能求出|MN|的最小值．（ⅱ）存在以原点为圆心且与直线MN相切的圆．设Rt△MON斜边上的高为h，当k=0时，h=，当k≠0时，|OM|•|ON|=，由此能推导出存在以原点为圆心，半径为且与直线MN相切的圆，并能求出圆的方程．解答：满分．（Ⅰ）解：由椭圆定义可知曲线C1的轨迹是椭圆，设C1的方程为，a＞b＞0，所以2a=2，c=1，则b=1，故的方程．…（Ⅱ）（ⅰ）证明：当k=0，M为C2长轴端点，则N为C1短轴的端点，|MN|=．…当k≠0时，设直线OM：y=kx，代入x2+=1，整理得（2+3k）x2=2，即x2=，y2=，所以|OM|2=x2+y2=．…又由已知OM⊥ON，设ON：y=﹣，同理解得|ON|2=，…所以|MN|2=|OM|2+|ON|2=+=（2+2k2）•，…又|MN|2﹣2==，所以|MN|的最小值为．…（ⅱ）解：存在以原点为圆心且与直线MN相切的圆．设Rt△MON斜边上的高为h，由（Ⅱ）（ⅰ）得当k=0时，h=，…当k≠0时，|OM|•|ON|=，又|MN|=，…由|MN|•h=|OM|•|ON|，得h==，故存在以原点为圆心，半径为且与直线MN相切的圆，圆方程为．…点评：本小题考查椭圆的标准方程与性质、直线与圆锥曲线的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、数形结合思想等．22．已知函数f（x）=lnx+．（1）求曲线y=f（x）在（2，f（2））处的切线方程；（2）若g（x）=f（x）﹣+ax2﹣2x有两个不同的极值点．其极小值为M，试比较2M与﹣3的大小，并说明理由；（3）设q＞p＞2，求证：当x∈（p，q）时，＞．考点：利用导数研究函数的极值；利用导数研究曲线上某点切线方程．专题：导数的综合应用．分析：（1）求出f（x）在该点处的导数，即得切线的斜率，用点斜式写出切线的方程；（2）利用导数求出函数g（x）的极小值M，即可比较2M与﹣3的大小；（3）用分析法证明x∈（p，q）时，成立，同理证得x∈（p，q）时，成立，即得所证结论．解答：解：（1）∵f（x）=lnx+，∴，∴；∴所求的切线方程为，即x﹣4y+4ln2=0；（2）∵g（x）=ax2﹣2x+lnx，∴；又∵g（x）有两个不同的极值点，∴p（x）=2ax2﹣2x+1=0在（0，+∞）有两个不同的根x1，x2（x1＜x2），则△＞0且x1+x2＞0，x1x2＞0，解得；∴g（x）在（0，x1）上递增，（x1，x2）上递减，（x2，+∞）上递增，∴g（x）的极小值；又∵，∴，则，∴M（x2）在（1，+∞）递减，∴，故2M＜﹣3；（3）先证明：当x∈（p，q）时，；即证：，只需证：；事实上，设，易得，∴u（x）在（p，q）内递增，∴u（x）＞u（p）=0，即原式成立；同理可证当x∈（p，q）时，；综上，当x∈（p，q）时，．点评：本题考查了利用导数求函数曲线上某一点处的切线方程的问题，利用导数研究函数的单调性与极值的问题，也考查了不等式的证明问题，是综合性问题．。

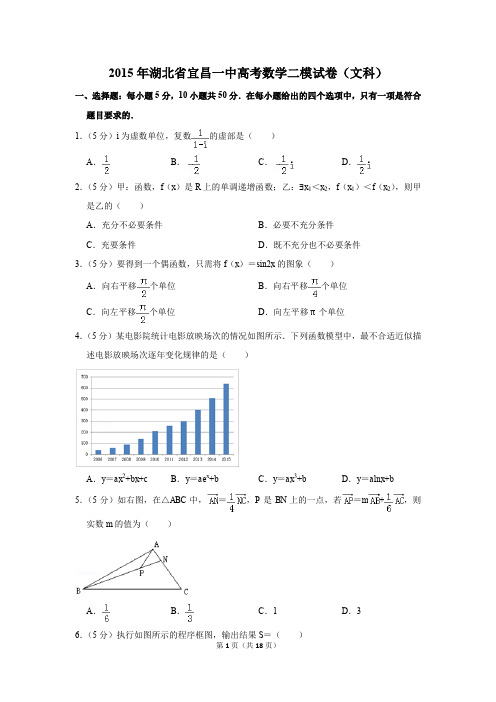
2015年湖北省宜昌一中高考数学二模试卷（文科）一、选择题：每小题5分，10小题共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）i为虚数单位，复数的虚部是（）A．B．C．D．2．（5分）甲：函数，f（x）是R上的单调递增函数；乙：∃x1＜x2，f（x1）＜f（x2），则甲是乙的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3．（5分）要得到一个偶函数，只需将f（x）＝sin2x的图象（）A．向右平移个单位B．向右平移个单位C．向左平移个单位D．向左平移π个单位4．（5分）某电影院统计电影放映场次的情况如图所示．下列函数模型中，最不合适近似描述电影放映场次逐年变化规律的是（）A．y＝ax2+bx+c B．y＝ae x+b C．y＝ax3+b D．y＝alnx+b5．（5分）如右图，在△ABC中，＝，P是BN上的一点，若＝m+，则实数m的值为（）A．B．C．1D．36．（5分）执行如图所示的程序框图，输出结果S＝（）A．2015B．2016C．﹣2015D．﹣20167．（5分）已知点P（x，y）的坐标满足条件，那么点P到直线3x﹣4y﹣13＝0的最小值为（）A．B．2C．D．18．（5分）设min{p，q}表示p，q两者中的较小者，若函数f（x）＝min{3﹣x，log2x}，则满足f（x）≤的x的集合为（）A．（0，2]∪[，+∞）B．[，]C．（0，]∪[，+∞）D．（0，）∪（，+∞）9．（5分）已知O、A、B三地在同一水平面内，A地在O地正东方向2km处，B地在O地正北方向2km处，某测绘队员在A、B之间的直线公路上任选一点C作为测绘点，用测绘仪进行测绘，O地为一磁场，距离其不超过km的范围内会测绘仪等电子仪器形成干扰，使测量结果不准确，则该测绘队员能够得到准确数据的概率是（）A．1﹣B．C．1﹣D．10．（5分）已知F为双曲线﹣＝1（a＞0，b＞0）的右焦点，a为双曲线虚轴的一个顶点，过点F、A的直线与双曲线的一条渐近线在y轴右侧的交点为B，若＝（﹣1），则此双曲线的离心率是（）A．B．C．2D．二、填空题：本大题共7个小题，每小题5分，共35分．把答案填在答题卡上对应题号后的横线上．答错位置，书写不清，模棱两可不得分．11．（5分）已知全集U＝[0，2]，集合M＝{x|x2﹣x≤0}，则∁u M＝．12．（5分）为了估计某水池中鱼的尾数，先从水池中捕出2000尾鱼，并给每尾鱼做上标记（不影响存活），然后放回水池，经过适当的时间，再从水池中捕出500尾鱼，其中有标记的鱼为40尾，根据上述数据估计该水池中鱼的数量约为尾．13．（5分）已知向量＝（3﹣x，y），＝（2，1），若∥，则3x+9y+2的最小值为．14．（5分）圆x2+y2＝4被直线l：kx﹣y﹣2k＝0截得的劣弧所对的圆心角的大小为，则直线l倾斜角的大小为．15．（5分）某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的全面积为（平方单位）．16．（5分）函数f（x）＝|x﹣a|﹣|x﹣2a|（a＞0），若对∀x∈R，都有f（2x）﹣1≤f（x），则实数a的最大值为．17．（5分）分形几何学是数学家伯努瓦•曼得尔布罗在20世纪70年代创立的一门新的数学学科，它的创立为解决传统科学众多领域的难题提供了全新的思路．按照如图甲所示的分形规律可得如图乙所示的一个树形图：记图乙中第n行白圈的个数为a n，则：（Ⅰ）a4＝；（Ⅱ）a n＝．三、解答题：本大题共5小题，共65分．解答应写出文字说明，证明过程或演算步骤．把答案填在答题卡上对应题号指定框内．18．（12分）已知f（x）＝sin（2x+）+sin2x﹣．（Ⅰ）求函数f（x）的对称中心；（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，若a＝2，f（）＝，cos（π﹣C）＝﹣，求b的大小．19．（12分）等差数列{a n}的前3项和S3＝9，且a1、a2、a5成等比数列．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）已知数列{a n}单调递增，T n为数列{}的前n项和，若T n≤λa n+1对一切n∈N*恒成立，求实数λ的最小值．20．（13分）如图所示，在四棱锥P﹣ABCD中，底面ABCD为正方形，侧棱P A⊥底面ABCD，P A＝AD＝1，E、F分别为PD、AC上的动点，且＝＝λ，（0＜λ＜1）．（Ⅰ）若λ＝，求证：EF∥平面P AB；（Ⅱ）求三棱锥E﹣FCD体积最大值．21．（14分）已知函数f（x）＝e x，x∈R．（Ⅰ）证明：曲线y＝f（x）与曲线y＝x+1有唯一公共点；（Ⅱ）（i）求g（x）＝x+2+（x﹣2）•f（x）在[0，+∞）的最小值；（ii）若实数a，b不相等，试比较与的大小，并说明理由．22．（14分）在直角坐标系中，已知点F（0，1），直线l：y＝﹣1，点H是直线l上任意一点，过点H垂直于l的直线交线段FH的中垂线于点M．记点M的轨迹为曲线Γ．（Ⅰ）求曲线Γ的方程；（Ⅱ）若A，B为曲线Γ上异于原点的任意两点，过A，B分别作曲线T的两条切线l1、l2，l1、l2相交于点P，且与x轴分别交于E、F，设△PEF与△OAB的面积分别为S1、S2．试问：是否存在实数λ使得S1＝λS2？若存在，求出λ的值；若不存在，请说明理由．2015年湖北省宜昌一中高考数学二模试卷（文科）参考答案与试题解析一、选择题：每小题5分，10小题共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）i为虚数单位，复数的虚部是（）A．B．C．D．【解答】解：复数＝＝的虚部是．故选：A．2．（5分）甲：函数，f（x）是R上的单调递增函数；乙：∃x1＜x2，f（x1）＜f（x2），则甲是乙的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【解答】解：根据函数单调性的定义可知，若f（x）是R上的单调递增函数，则∀x1＜x2，f（x1）＜f（x2），成立，∴命题乙成立．若：∃x1＜x2，f（x1）＜f（x2），则不满足函数单调性定义的任意性，∴命题甲不成立．∴甲是乙成立的充分不必要条件．故选：A．3．（5分）要得到一个偶函数，只需将f（x）＝sin2x的图象（）A．向右平移个单位B．向右平移个单位C．向左平移个单位D．向左平移π个单位【解答】解：函数y＝﹣cos2x＝sin（2x﹣）＝sin[2（x﹣）]，所以只需把函数y＝sin2x 的图象，向右平移个长度单位，即可得到函数y＝sin（2x﹣）＝﹣cos2x的图象．故选：B．4．（5分）某电影院统计电影放映场次的情况如图所示．下列函数模型中，最不合适近似描述电影放映场次逐年变化规律的是（）A．y＝ax2+bx+c B．y＝ae x+b C．y＝ax3+b D．y＝alnx+b【解答】解：根据图象得出单调性的规律，单调递增，速度越来越快，∵y＝ax2+bx+c，单调递增，速度越来越快，y＝ae x+b，指数型函数增大很快，y＝e ax+b，指数型函数增大很快，y＝alnx+b，对数型函数增大速度越来越慢，所以A，B，C都有可能，D不可能．故选：D．5．（5分）如右图，在△ABC中，＝，P是BN上的一点，若＝m+，则实数m的值为（）A．B．C．1D．3【解答】解：由题意，设＝n，则＝+＝+n＝+n（﹣）＝+n（﹣）＝+n（﹣）＝（1﹣n）+，又∵＝m+，∴m＝1﹣n，且＝解得；n＝，m＝，故选：A．6．（5分）执行如图所示的程序框图，输出结果S＝（）A．2015B．2016C．﹣2015D．﹣2016【解答】解：根据程序框图可知该程序的功能是计算S＝﹣1+3﹣5+7﹣…+（﹣1）2015•（2•2015﹣1），则根据数列求和的并项法可得S═﹣1+3﹣5+7﹣…+（﹣1）2015•（2•2015﹣1）＝﹣1+（﹣5+3）+（﹣9+7）+…+（﹣4029+4027）＝﹣1+（﹣2）•＝﹣2015，故选：C．7．（5分）已知点P（x，y）的坐标满足条件，那么点P到直线3x﹣4y﹣13＝0的最小值为（）A．B．2C．D．1【解答】解：由约束条件作出可行域如图，由图可知，当P与A（1，0）重合时，P到直线3x﹣4y﹣13＝0的距离最小为d＝．故选：B．8．（5分）设min{p，q}表示p，q两者中的较小者，若函数f（x）＝min{3﹣x，log2x}，则满足f（x）≤的x的集合为（）A．（0，2]∪[，+∞）B．[，]C．（0，]∪[，+∞）D．（0，）∪（，+∞）【解答】解：根据min{p，q}表示p，q两者中的较小者，得到函数f（x）＝min{﹣x+3，log2x}的图象，如图所示：当x＝或时，y＝，由图象可知：f（x）≤的解集为（0，]∪[，+∞）．故选：C．9．（5分）已知O、A、B三地在同一水平面内，A地在O地正东方向2km处，B地在O地正北方向2km处，某测绘队员在A、B之间的直线公路上任选一点C作为测绘点，用测绘仪进行测绘，O地为一磁场，距离其不超过km的范围内会测绘仪等电子仪器形成干扰，使测量结果不准确，则该测绘队员能够得到准确数据的概率是（）A．1﹣B．C．1﹣D．【解答】解：由题意，△AOB是直角三角形，OA＝OB＝2，所以AB＝2，O地为一磁场，距离其不超过km的范围为个圆，与AB相交于C，D两点，作OE⊥AB，则OE＝，所以CD＝2，所以该测绘队员能够得到准确数据的概率是1﹣＝1﹣．故选：A．10．（5分）已知F为双曲线﹣＝1（a＞0，b＞0）的右焦点，a为双曲线虚轴的一个顶点，过点F、A的直线与双曲线的一条渐近线在y轴右侧的交点为B，若＝（﹣1），则此双曲线的离心率是（）A．B．C．2D．【解答】解：设F（c，0），A（0，b），渐近线方程为y＝x，则直线AF的方程为，与y＝x联立可得B（，﹣），∵＝（﹣1），∴（，﹣﹣b）＝（﹣1）（c，﹣b），∴c＝（+1），∴e＝＝，故选：A．二、填空题：本大题共7个小题，每小题5分，共35分．把答案填在答题卡上对应题号后的横线上．答错位置，书写不清，模棱两可不得分．11．（5分）已知全集U＝[0，2]，集合M＝{x|x2﹣x≤0}，则∁u M＝（1，2]．【解答】解：全集U＝[0，2]，集合M＝{x|x2﹣x≤0}＝{x|0≤x≤1}，则∁u M＝{x|1＜x≤2}．故答案为：（1，2]．12．（5分）为了估计某水池中鱼的尾数，先从水池中捕出2000尾鱼，并给每尾鱼做上标记（不影响存活），然后放回水池，经过适当的时间，再从水池中捕出500尾鱼，其中有标记的鱼为40尾，根据上述数据估计该水池中鱼的数量约为25000尾．【解答】解：由题意可得有记号的鱼所占的比例大约为，设水库内鱼的尾数是x，则有，解得x＝25000，故答案为：2500013．（5分）已知向量＝（3﹣x，y），＝（2，1），若∥，则3x+9y+2的最小值为6 +2．【解答】解：∵＝（3﹣x，y），＝（2，1），切∥，∴（3﹣x）•1﹣2y＝0，∴x+2y＝3，∴3x+9y+2＝3x+32y+2≥2+2＝2+2＝6+2，∴3x+9y+2的最小值为6+2，故答案为：6+2．14．（5分）圆x2+y2＝4被直线l：kx﹣y﹣2k＝0截得的劣弧所对的圆心角的大小为，则直线l倾斜角的大小为或．【解答】解：直线l：kx﹣y﹣2k＝0变形为k（x﹣2）﹣y＝0，∴该直线过定点P（2，0）；又圆x2+y2＝4被直线l：kx﹣y﹣2k＝0截得的劣弧所对的圆心角为，如图所示；∴∠POA＝，∴A（1，）；∴直线的斜率为k P A＝＝﹣，∴直线l倾斜角为；同理，B（1，﹣），k PB＝，∴直线l的倾斜角为；综上，直线l倾斜角为或．故答案为：或．15．（5分）某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的全面积为20+2（平方单位）．【解答】解：三视图复原的几何体是长方体，长方体长、宽、高分别是：2，2，3，几何体的底面为正方形，面积为：2×2＝4，几何体的侧面为四个直角梯形，面积为：2×（1+2）×2+2×（2+3）×2＝16，几何体的截面是一个边长为的菱形，且两条对角线长度分别为：2和2，面积为：×＝2，故几何体的全面积为：20+2，故答案为：20+2．16．（5分）函数f（x）＝|x﹣a|﹣|x﹣2a|（a＞0），若对∀x∈R，都有f（2x）﹣1≤f（x），则实数a的最大值为．【解答】解：f（2x）﹣1≤f（x），（a＞0）恒成立，即|2x﹣a|﹣|2x﹣2a|﹣1≤|x﹣a|﹣|x﹣2a|恒成立，即|2x﹣a|+|x﹣2a|≤3|x﹣a|+1恒成立．此不等式中，绝对值的“根”共有4个：，a，a，2a，当x＜时，不等式即a﹣2x+2a﹣x≤3a﹣3x+1，即0≤1．当≤x＜a时，不等式即2x﹣a+2a﹣x≤3a﹣3x+1，即4x≤2a+1，故有4a≤2a+1，即a．当a≤x＜2a时，不等式即2x﹣a+2a﹣x≤3x﹣3a+1，即4a≤2x+1，故4a≤4a+1，可得0≤1．成立．当x≥2a时，不等式即2x﹣a+x﹣2a≤3x﹣3a+1，即0≤1．综上可得，a≤，故a的最大值为，故答案为：．17．（5分）分形几何学是数学家伯努瓦•曼得尔布罗在20世纪70年代创立的一门新的数学学科，它的创立为解决传统科学众多领域的难题提供了全新的思路．按照如图甲所示的分形规律可得如图乙所示的一个树形图：记图乙中第n行白圈的个数为a n，则：（Ⅰ）a4＝14；（Ⅱ）a n＝．【解答】解：（Ⅰ）根据图甲所示的分形规律，1个白圈分形为2个白圈1个黑圈，1个黑圈分形为1个白圈2个黑圈，记某行白圈x个，黑圈y个为（x，y），则第一行记为（1，0），第二行记为（2，1），第三行记为（5，4），第四行记为（14，13）故a4＝14（Ⅱ）各行白圈数乘以2，分别是2，4，10，28，82，即1+1，3+1，9+1，27+1，81+1，∴第n行的白圈数为，故答案为：14，三、解答题：本大题共5小题，共65分．解答应写出文字说明，证明过程或演算步骤．把答案填在答题卡上对应题号指定框内．18．（12分）已知f（x）＝sin（2x+）+sin2x﹣．（Ⅰ）求函数f（x）的对称中心；（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，若a＝2，f（）＝，cos（π﹣C）＝﹣，求b的大小．【解答】解：（Ⅰ）f（x）＝sin（2x+）+sin2x﹣＝sin2x+cos2x+＝sin2x所以f（x）对称中心是（，0），k∈Z．（Ⅱ）由f（）＝，得f（）＝sin A＝，即sin A＝，若cos A＝，而sin（A+C）＝又sin（A+C）＝2cos C，所以cos C＝sin C，所以cos C＝，所以sin B＝sin（A+C）＝cos C＝（10分）由正弦定理得：b＝＝4．（12分）19．（12分）等差数列{a n}的前3项和S3＝9，且a1、a2、a5成等比数列．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）已知数列{a n}单调递增，T n为数列{}的前n项和，若T n≤λa n+1对一切n∈N*恒成立，求实数λ的最小值．【解答】解：（Ⅰ）设a n＝a1+（n﹣1）d，S n＝na1+，由S3＝9，a1+d＝3，∵a1，a2，a5成等比数列，∴a1（a1+4d）＝（a1+4d）2∴a1＝1，d＝2，或a n＝3，d＝0故a n＝2n﹣1，S n＝n2，或a n＝3，S n＝3n，（Ⅱ）∵＝＝（）∴T n＝（1﹣+…+）∴T n＝，T n≤λa n+1对n∈N*恒成立∴≤λ（2n+1），＝∵4n在[1，+∞）单调递增，在[1，+∞）单调递减；∴n＝1时，最大值为；∴，即λ最小值为．20．（13分）如图所示，在四棱锥P﹣ABCD中，底面ABCD为正方形，侧棱P A⊥底面ABCD，P A＝AD＝1，E、F分别为PD、AC上的动点，且＝＝λ，（0＜λ＜1）．（Ⅰ）若λ＝，求证：EF∥平面P AB；（Ⅱ）求三棱锥E﹣FCD体积最大值．【解答】（Ⅰ）证明：分别取P A和AB中点M、N，连接MN、ME、NF，则NF AD，ME AD，所以NF ME，∴四边形MEFN为平行四边形．∴EF∥MN，又EF⊈平面P AB，MN⊂平面P AB，∴EF∥平面P AB．（Ⅱ）解：在平面P AD内作EH⊥AD于H，因为侧棱P A⊥底面ABCD，所以平面P AD⊥底面ABCD，且平面P AD∩底面ABCD＝AD，所以EH⊥平面ADC，所以EH∥P A．因为（0＜λ＜1），所以，EH＝λP A＝λ．＝＝1﹣λ，，V E﹣DFC＝×λ＝＝，（0＜λ＜1），∴三棱锥E﹣FCD体积最大值．21．（14分）已知函数f（x）＝e x，x∈R．（Ⅰ）证明：曲线y＝f（x）与曲线y＝x+1有唯一公共点；（Ⅱ）（i）求g（x）＝x+2+（x﹣2）•f（x）在[0，+∞）的最小值；（ii）若实数a，b不相等，试比较与的大小，并说明理由．【解答】（Ⅰ）证明：曲线y＝f（x）与曲线y＝x+1有唯一公共点等价于方程e x＝x+1有唯一实数解．设h（x）＝e x﹣x﹣1，则h′（x）＝e x﹣1，当x＜0时，h′（x）＜0，h（x）在（﹣∞，0）上单调递减，当x＞0时，h′（x）＞0，h（x）在（0，+∞）上单调递增．即有h（x）≥h（0）＝0，故h（x）＝0有唯一的实数解x＝0，原命题得证．（Ⅱ）（i）g（x）＝x+2+（x﹣2）•f（x）（x≥0）∴g′（x）＝1+（x﹣1）•e x，g′′（x）＝xe x≥0，即有g′（x）在[0，+∞）上单调递增且g′（0）＝0，则g′（x）≥0，g（x）在[0，+∞）上单调递增，则g（x）min＝g（0）＝0．（ii）﹣＝＝e a•由（i）可知，令a＜b，x＝b﹣a＞0，则x+2+（x﹣2）•e x＞0，此时，当a＜b时，＞，同理可证a＞b时，＞．22．（14分）在直角坐标系中，已知点F（0，1），直线l：y＝﹣1，点H是直线l上任意一点，过点H垂直于l的直线交线段FH的中垂线于点M．记点M的轨迹为曲线Γ．（Ⅰ）求曲线Γ的方程；（Ⅱ）若A，B为曲线Γ上异于原点的任意两点，过A，B分别作曲线T的两条切线l1、l2，l1、l2相交于点P，且与x轴分别交于E、F，设△PEF与△OAB的面积分别为S1、S2．试问：是否存在实数λ使得S1＝λS2？若存在，求出λ的值；若不存在，请说明理由．【解答】解：（Ⅰ）由题意|MF|＝|MH|，所以M点的轨迹为以点F（0，1）为焦点，直线l：y＝﹣1为准线的抛物线，所以曲线Γ的方程为x2＝4y；…（4分）（Ⅱ）当直线AB斜率不存在时显然不合题意；设直线AB的方程为y＝kx+b，与椭圆方程联立消去y得x2﹣4kx﹣4b＝0．设A（x1，y1），B（x2，y2），则x1+x2＝4k，x1x2＝﹣4b，…（6分）曲线Γ的方程为y＝x2，y′＝x，切线P A：y＝x1（x﹣x1）+y1，切线PB：y＝x2（x﹣x2）+y2，…（8分）P（2k，﹣2b），E（x1﹣，0），F（x2﹣，0）（10分）线段|EF|＝|x2﹣x1+﹣|，化简得|EF|＝|x2﹣x1|，所以S1＝|EF|y P＝b|x2﹣x1|，S2＝b|x2﹣x1|，…（13分）所以存在λ＝，使得S1＝S2．…（14分）。

湖北省宜昌一中2015届高考数学三模试卷（文科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．在复平面内，复数对应的点的坐标是( )A．（﹣1，1）B．（﹣1，﹣1）C．（1，﹣1）D．（1，1）2．设A，B为两个不相等的集合，条件p：x∉（A∩B），条件q：x∉（A∪B），则p是q的( ) A．充分不必要条件B．充要条件C．必要不充分条件D．既不充分也不必要条件3．已知a=2log32，，，则a，b，c的大小关系是( )A．a＞b＞c B．c＞b＞a C．c＞a＞b D．a＞c＞b4．阅读如图的程序框图，运行相应的程序则输出的K和S值分别为( )A．9，B．11，C．13，D．15，5．甲、乙两名同学在5次体能测试中的成绩的茎叶图如图所示，设，分别表示甲、乙两名同学测试成绩的平均数，s1，s2分别表示甲、乙两名同学测试成绩的标准差，则有( )A．，s1＜s2B．，s1＞s2C．，s1＞s2D．，s1=s26．已知函数y=a+sinbx（b＞0且b≠1）的图象如图所示，那么函数y=log b（x﹣a）的图象可能是( )A．B．C．D．7．已知双曲线（a＞0，b＞0）的一条渐近线方程是x﹣y=0，它的一个焦点在抛物线y2=﹣4x的准线上，则双曲线的方程为( )A．4x2﹣12y2=1 B．4x2﹣y2=1 C．12x2﹣4y2=1 D．x2﹣4y2=18．已知函数f（x）=sinωx﹣cosωx（ω＞0）的图象与x轴的两个相邻交点的距离等于，若将函数y=f（x）的图象向左平移个单位得到函数y=g（x）的图象，则y=g（x）是减函数的区间为( )A．（﹣，0）B．（﹣，）C．（0，）D．（，）9．在平面直角坐标系xOy中，点A（0，3），直线l：y=2x﹣4，设圆C的半径为1，圆心C 在l上．若圆C上存在点M，使|MA|=2|MO|，则圆心C的横坐标a的取值范围为( )A．[0，] B．（0，）C．（1，3）D．[1，3]10．已知函数f（x）=|mx|﹣|x﹣1|（m＞0），若关于x的不等式f（x）＜0的解集中的整数恰有3个，则实数m的取值范围为( )A．0＜m≤1B．≤m＜C．1＜m＜D．≤m＜2二、填空题：本大题共7小题，每小题5分，共35分，请将答案填在答题卡对应题号的位置上，答错位置，书写不清，模棱两可均不得分．11．已知集合M={﹣1，1}，，则M∩N=__________．12．某中学采用系统抽样的方法从该校2014-2015学年高一年级全体800名学生中抽取50名学生进行体能测试．现将800名学生从1到800进行编号，求得间隔数k==16．若从1～16中随机抽取1个数的结果是抽到了7，则在编号为33～48的这16个学生中抽取的一名学生其编号应该是__________．13．若向量，满足||=||=|+|=1，则•的值为__________．14．如图是某几何体的三视图，则该几何体的体积为__________．15．在平面区域内任取一点P（x，y），若（x，y）满足x+y≤b的概率大于，则b的取值范围是__________．16．如图，我们知道，圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形，又圆环的面积S=π（R2﹣r2）=（R﹣r）×2π×．所以，圆环的面积等于是以线段AB=R﹣r为宽，以AB中点绕圆心O旋转一周所形成的圆的周长2π×为长的矩形面积．请将上述想法拓展到空间，并解决下列问题：若将平面区域M={（x，y）|（x﹣d）2+y2≤r2}（其中0＜r＜d）绕y轴旋转一周，则所形成的旋转体的体积是__________．（结果用d，r表示）17．若函数y=f（x）在定义域内给定区间[a，b]上存在x o（a＜x o＜b），满足f（x o）=，则称函数y=f（x）是[a，b]上的“平均值函数”，x o是它的一个均值点．例如y=|x|是[﹣2，2]上的“平均值函数”，O就是它的均值点．（1）若函数，f（x）=x2﹣mx﹣1是[﹣1，1]上的“平均值函数”，则实数m的取值范围是__________．（2）若f（x）=㏑x是区间[a，b]（b＞a≥1）上的“平均值函数”，x o是它的一个均值点，则㏑x o与的大小关系是__________．三、解答题：本大题共5小题，共65分.解答应写出文字说明、证明过程或演算步骤．18．如图，已知点A（3，4），C（2，0），点O为坐标原点，点B在第二象限，且|OB|=3，记∠AOC=θ．高．（Ⅰ）求sin2θ的值；（Ⅱ）若AB=7，求△BOC的面积．19．在等差数列{a n}中，a2+a7=﹣23，a3+a8=﹣29．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设数列{a n+b n}是首项为1，公比为c的等比数列，求{b n}的前n项和S n．20．如图所示，四棱锥P﹣ABCD的底面ABCD是直角梯形，BC∥AD，AB⊥AD，AB=BC=AD，PA⊥底面ABCD，过BC的平面交PD于M，交PA于N（M与D不重合）．（1）求证：MN∥BC；（2）如果BM⊥AC，求此时的值．21．已知离心率为的椭圆的右焦点F是圆（x﹣1）2+y2=1的圆心，过椭圆上的动点P作圆的两条切线分别交y轴于M、N两点．（1）求椭圆的方程；（2）求线段MN长的最大值，并求此时点P的坐标．22．设函数f（x）=e x（lnx﹣a），e是自然对数的底数，e≈2.718…，a∈R且为常数．（1）若y=f（x）在x=1处的切线的斜率为2e，求a的值；（2）若y=f（x）在区间[ln2，ln3]上为单调函数，求a的取值范围．湖北省宜昌一中2015届高考数学三模试卷（文科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．在复平面内，复数对应的点的坐标是( )A．（﹣1，1）B．（﹣1，﹣1）C．（1，﹣1）D．（1，1）考点：复数的代数表示法及其几何意义；复数代数形式的乘除运算．专题：数系的扩充和复数．分析：直接由复数代数形式的乘除运算化简复数，则答案可求．解答：解：由=，则复数对应的点的坐标是：（﹣1，1）．故选：A．点评：本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．2．设A，B为两个不相等的集合，条件p：x∉（A∩B），条件q：x∉（A∪B），则p是q的( ) A．充分不必要条件B．充要条件C．必要不充分条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：集合；简易逻辑．分析：根据集合关系，以及充分条件和必要条件的定义进行判断即可．解答：解：当x∈A，且x∉（A∩B），满足x∈（A∪B），即充分性不成立，若x∉（A∪B，则x∉（A∩B），成立，即必要性成立，故p是q必要不充分条件，故选：C点评：本题主要考查充分条件和必要条件的判断，根据集合关系是解决本题的关键．3．已知a=2log32，，，则a，b，c的大小关系是( ) A．a＞b＞c B．c＞b＞a C．c＞a＞b D．a＞c＞b考点：对数值大小的比较．专题：函数的性质及应用．分析：分别判断a，b，c的取值范围即可．解答：解：a=2log32=log34＞1，=，=＜1，则a＞c＞b，故选：D．点评：本题主要考查函数值的大小比较，根据指数函数和对对数函数的性质是解决本题的关键．4．阅读如图的程序框图，运行相应的程序则输出的K和S值分别为( )A．9，B．11，C．13，D．15，考点：程序框图．专题：图表型；算法和程序框图．分析：模拟执行程序框图，依次写出每次循环得到的s，K的值，当K=11时，满足条件K＞10，退出循环，输出K的值为11，s的值为．解答：解：模拟执行程序框图，可得s=0，K=1不满足条件K＞10，s=，K=3不满足条件K＞10，s=，K=5不满足条件K＞10，s=，K=7不满足条件K＞10，s=，K=9不满足条件K＞10，s=，K=11满足条件K＞10，退出循环，输出K的值为11，s的值为．故选：B．点评：本题主要考查了循环结构的程序框图，依次正确写出每次循环得到的s，K的值是解题的关键，属于基本知识的考查．5．甲、乙两名同学在5次体能测试中的成绩的茎叶图如图所示，设，分别表示甲、乙两名同学测试成绩的平均数，s1，s2分别表示甲、乙两名同学测试成绩的标准差，则有( )A．，s1＜s2B．，s1＞s2C．，s1＞s2D．，s1=s2考点：茎叶图．专题：概率与统计．分析：根据茎叶图中的数据，计算出甲、乙同学测试成绩的平均数与方差、标准差，即可得出结论．解答：解：根据茎叶图中的数据，得；甲同学测试成绩的平均数是=（76+76+82+88+88）=82，乙同学测试成绩的平均数是=（76+78+83+86+87）=82；甲同学测试成绩的方差是：=[（76﹣82）2+（76﹣82）2+（82﹣82）2+（88﹣82）2+（88﹣82）2]=，标准差是s1=，乙同学测试成绩的方差是=[（﹣6）2+（﹣4）2+12+（4）2+52]=，标准差是s2=．∴=，s1＞s2．故选：B．点评：本题考查了茎叶图的应用问题，也考查了平均数、方差、标准差的计算问题，是基础题．6．已知函数y=a+sinbx（b＞0且b≠1）的图象如图所示，那么函数y=log b（x﹣a）的图象可能是( )A．B．C．D．考点：函数的图象．专题：函数的性质及应用．分析：先根据正弦函数的图象得到a，b的取值范围，再根据对数函数的图象和性质得到答案．解答：解：函数y=a+sinbx（b＞0且b≠1）的图象，是有y=sinbx的图象向上平移a的单位得到的，由图象可知1＜a＜2，由图象可知函数的最小正周期＜T＜π，∴＜＜π，解得2＜b＜4，∴y=log b x的图象过定点（1，0）且为增函数，∵y=log b（x﹣a）函数的图象是由y=log b x图象向右平移a的单位得到，∴y=log b（x﹣a）函数的图象过定点（a+1，0），其中2＜a+1＜3，故选：C点评：本题考查了正弦函数的图象和对数函数的图象，属于基础题．7．已知双曲线（a＞0，b＞0）的一条渐近线方程是x﹣y=0，它的一个焦点在抛物线y2=﹣4x的准线上，则双曲线的方程为( )A．4x2﹣12y2=1 B．4x2﹣y2=1 C．12x2﹣4y2=1 D．x2﹣4y2=1考点：抛物线的简单性质；双曲线的标准方程．专题：圆锥曲线的定义、性质与方程．分析：利用双曲线的渐近线的方程可得a：b=：1，再利用抛物线的准线x=1=c及c2=a2+b2即可得出a、b．得到椭圆方程．解答：解：∵双曲线（a＞0，b＞0）的一条渐近线方程是x﹣y=0，∴a：b=：1，∵双曲线的一个焦点在抛物线y2=﹣4x的准线x=1上，∴c=1．c2=a2+b2，解得：b2=，a2=∴此双曲线的方程为：x2﹣4y2=1．故选：D．点评：本题考查的知识点是抛物线的简单性质和双曲线的简单性质，熟练掌握圆锥曲线的图象和性质是解题的关键．8．已知函数f（x）=sinωx﹣cosωx（ω＞0）的图象与x轴的两个相邻交点的距离等于，若将函数y=f（x）的图象向左平移个单位得到函数y=g（x）的图象，则y=g（x）是减函数的区间为( )A．（﹣，0）B．（﹣，）C．（0，）D．（，）考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：由已知可求出函数f（x）的解析式，进而根据函数图象的平移变换法则得到函数y=g （x）的解析式，根据正弦函数的性质分析出函数的单调性后，比照四个答案即可得到结论．解答：解：∵函数f（x）=sinωx﹣cosωx=2sin（ωx﹣），又∵函数f（x）=sinωx﹣cosωx（ω＞0）的图象与x轴的两个相邻交点的距离等于=，故函数的最小正周期T=π，又∵ω＞0，∴ω=2，故f（x）=2sin（2x﹣），将函数y=f（x）的图象向左平移个单位可得y=g（x）=2sin[2（x+）﹣]=2sin2x的图象，令+2kπ≤2x≤+2kπ，即+kπ≤x≤+kπ，k∈Z，故函数y=g（x）的减区间为[+kπ，+kπ]，k∈Z，当k=0时，区间[，]为函数的一个单调递减区间，又∵（，）⊆[，]，故选：D．点评：本题考查的知识点是函数y=Asin（ωx+φ）的图象变换，两角和与差的正弦函数，正弦函数的单调性，熟练掌握正弦型函数的图象性质及变换法则是解答本题的关键，属于中档题．9．在平面直角坐标系xOy中，点A（0，3），直线l：y=2x﹣4，设圆C的半径为1，圆心C 在l上．若圆C上存在点M，使|MA|=2|MO|，则圆心C的横坐标a的取值范围为( )A．[0，] B．（0，）C．（1，3）D．[1，3]考点：直线与圆的位置关系．专题：计算题；直线与圆．分析：设出圆心C的坐标，表示出圆的方程，进而根据|MA|=2|MO|，设出M，利用等式关系整理求得M的轨迹方程，进而判断出点M应该既在圆C上又在圆D上，且圆C和圆D有交点．进而确定不等式关系求得a的范围．解答：解：因为圆C的圆心在直线y=2x﹣4上，所以设圆心C为（a，2a﹣4），则圆C的方程为：（x﹣a）2+[y﹣（2a﹣4）]2=1．又|MA|=2|MO|，设M为（x，y），则可得：x2+（y+1）2=4，设该方程对应的圆为D，所以点M应该既在圆C上又在圆D上，且圆C和圆D有交点．则|2﹣1|≤≤|2+1|．由5a2﹣12a+8≥0，得a∈R．由5a2﹣12a≤0得0≤a≤．所以圆心C的横坐标的取值范围为[0，]．故选：A．点评：本题主要考查了直线与圆的方程的应用．考查了学生的分析推理和基本的运算能力．10．已知函数f（x）=|mx|﹣|x﹣1|（m＞0），若关于x的不等式f（x）＜0的解集中的整数恰有3个，则实数m的取值范围为( )A．0＜m≤1B．≤m＜C．1＜m＜D．≤m＜2考点：函数的零点与方程根的关系．专题：计算题；作图题；函数的性质及应用；不等式的解法及应用．分析：f（x）＜0可化为|mx|＜|x﹣1|，作函数y=|mx|与函数y=|x﹣1|的图象，由数形结合求解即可．解答：解：f（x）＜0可化为|mx|＜|x﹣1|，作函数y=|mx|与函数y=|x﹣1|的图象如下，结合图象可知，关于x的不等式f（x）＜0的解集中的3个整数解为0，﹣1，﹣2；故只需使，解得，≤m＜；故选：B．点评：本题考查了不等式的解与函数的图象的关系应用，属于基础题．二、填空题：本大题共7小题，每小题5分，共35分，请将答案填在答题卡对应题号的位置上，答错位置，书写不清，模棱两可均不得分．11．已知集合M={﹣1，1}，，则M∩N={﹣1}．考点：交集及其运算．专题：计算题．分析：把集合N中的不等式变形后，利用指数函数的单调性列出关于x的不等式，求出解集中的整数解即可得到集合N的元素，然后利用求交集的法则求出M与N的交集即可．解答：解：集合N中的不等式可化为：2﹣1＜2x+1＜22，因为2＞1，所以指数函数y=2x为增函数，则﹣1＜x+1＜2即﹣2＜x＜1，由x∈Z得到x的值可以是﹣1和0所以N={﹣1，0}，则M∩N═{﹣1，1}∩{﹣1，0}={﹣1}故答案为：{﹣1}点评：本题属于以函数的单调性为平台，求集合的交集的基础题，是2015届高考常会考的题型．12．某中学采用系统抽样的方法从该校2014-2015学年高一年级全体800名学生中抽取50名学生进行体能测试．现将800名学生从1到800进行编号，求得间隔数k==16．若从1～16中随机抽取1个数的结果是抽到了7，则在编号为33～48的这16个学生中抽取的一名学生其编号应该是39．考点：系统抽样方法．专题：概率与统计．分析：根据系统抽样的定义进行求解．解答：解：∵样本间隔k=16，若从1～16中随机抽取1个数的结果是抽到了7，∴抽取的号码数为7+16x，当x=2时，7+16×2=39，即在编号为33～48的这16个学生中抽取的一名学生其编号应该39，故答案为：39点评：本题主要考查系统抽样的应用，比较基础．13．若向量，满足||=||=|+|=1，则•的值为﹣．考点：平面向量数量积的运算．专题：平面向量及应用．分析：利用向量的数量积运算即可得出．解答：解：∵向量，满足||=||=|+|=1，∴，化为，即1，解得．故答案为．点评：熟练掌握向量的数量积运算是解题的关键．14．如图是某几何体的三视图，则该几何体的体积为．考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：由已知中的三视图，可知该几何体是一个以俯视图为底面的四棱锥，求出底面面积，代入棱锥体积公式，可得答案．解答：解：由已知中的三视图，可知该几何体是一个以俯视图为底面的四棱锥，其底面面积S=1×1=1，高h=1，故棱锥的体积V==，故答案为：点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．15．在平面区域内任取一点P（x，y），若（x，y）满足x+y≤b的概率大于，则b的取值范围是（1，+∞）．考点：几何概型．专题：概率与统计．分析：先求出满足x+y≤b的概率等于对应的直线方程即可得到结论．解答：解：作出不等式组对应的平面区域如图：则矩形的面积S=2×2=4，当满足x+y≤b的概率大于，则满足x+y≤b对应的区域为△OED，则E（b，0），D（0，b），（b＞0），则△OED的面积S=×，即，即b2=1，解得b=1，若满足x+y≤b的概率大于，则对应区域的面积S＞S△OED，此时直线x+y=b在直线x+y=1的上方，即b＞1，故b的取值范围是（1，+∞），故答案为：（1，+∞）点评：本题主要考查几何概型的概率计算，根据条件求出概率等于对应的直线方程是解决本题的关键．16．如图，我们知道，圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形，又圆环的面积S=π（R2﹣r2）=（R﹣r）×2π×．所以，圆环的面积等于是以线段AB=R﹣r为宽，以AB中点绕圆心O旋转一周所形成的圆的周长2π×为长的矩形面积．请将上述想法拓展到空间，并解决下列问题：若将平面区域M={（x，y）|（x﹣d）2+y2≤r2}（其中0＜r＜d）绕y轴旋转一周，则所形成的旋转体的体积是2π2r2d．（结果用d，r表示）考点：旋转体（圆柱、圆锥、圆台）；归纳推理．专题：空间位置关系与距离．分析：根据已知中圆环的面积等于是以线段AB=R﹣r为宽，以AB中点绕圆心O旋转一周所形成的圆的周长2π×为长的矩形面积．拓展到空间后，将平面区域M={（x，y）|（x﹣d）2+y2≤r2}（其中0＜r＜d）绕y轴旋转一周，则所形成的旋转体的体积应等于：以圆（x ﹣d）2+y2=r2为底面，以圆心（d，0）绕y轴旋转一周形成的圆的周长2π×d为高的圆柱的体积．代入可得答案．解答：解：由已知中圆环的面积等于是以线段AB=R﹣r为宽，以AB中点绕圆心O旋转一周所形成的圆的周长2π×为长的矩形面积．拓展到空间后，将平面区域M={（x，y）|（x﹣d）2+y2≤r2}（其中0＜r＜d）绕y轴旋转一周，则所形成的旋转体的体积应等于：以圆（x﹣d）2+y2=r2为底面，以圆心（d，0）绕y轴旋转一周形成的圆的周长2π×d为高的圆柱的体积．故V=πr2•2πd=2π2r2d，故答案为：2π2r2d．点评：本题考查的知识点是圆柱的体积，类比推理，其中得到拓展到空间后，将平面区域M={（x，y）|（x﹣d）2+y2≤r2}（其中0＜r＜d）绕y轴旋转一周，则所形成的旋转体的体积应等于：以圆（x﹣d）2+y2=r2为底面，以圆心（d，0）绕y轴旋转一周形成的圆的周长2π×d 为高的圆柱的体积．是解答的关键．17．若函数y=f（x）在定义域内给定区间[a，b]上存在x o（a＜x o＜b），满足f（x o）=，则称函数y=f（x）是[a，b]上的“平均值函数”，x o是它的一个均值点．例如y=|x|是[﹣2，2]上的“平均值函数”，O就是它的均值点．（1）若函数，f（x）=x2﹣mx﹣1是[﹣1，1]上的“平均值函数”，则实数m的取值范围是（0，2）．（2）若f（x）=㏑x是区间[a，b]（b＞a≥1）上的“平均值函数”，x o是它的一个均值点，则㏑x o与的大小关系是．考点：二次函数的性质．专题：函数的性质及应用．分析：（1）函数f（x）=x2﹣mx﹣1是区间[﹣1，1]上的平均值函数，故有x2﹣mx﹣1=在（﹣1，1）内有实数根，求出方程的根，让其在（﹣1，1）内，即可求出实数m的取值范围．（2）（2）猜想判断，换元转化为h（t）=2lnt﹣t，利用导数证明，求解出最值得出）=2lnt﹣t+＜h（1）=0，解答：解：∵函数f（x）=x2﹣mx﹣1是区间[﹣1，1]上的平均值函数，∴关于x的方程x2﹣mx﹣1=在（﹣1，1）内有实数根．即x2﹣mx﹣1=﹣m在（﹣1，1）内有实数根．即x2﹣mx+m﹣1=0，解得x=m﹣1，x=1．又1∉（﹣1，1）∴x=m﹣1必为均值点，即﹣1＜m﹣1＜1⇒0＜m＜2．∴所求实数m的取值范围是（0，2）．故答案为：（0，2）（2）解：由题知lnx0=．猜想：，证明如下：，令t=＞1，原式等价于lnt2，2lnt﹣t+＜0，令h（t）=2lnt﹣t+（t＞1），则h′（t）=﹣1﹣=﹣＜0，∴h（t）=2lnt﹣t+＜h（1）=0，得证点评：本题主要是在新定义下考查二次方程根的问题．在做关于新定义的题目时，一定要先认真的研究定义理解定义，再按定义做题．三、解答题：本大题共5小题，共65分.解答应写出文字说明、证明过程或演算步骤．18．如图，已知点A（3，4），C（2，0），点O为坐标原点，点B在第二象限，且|OB|=3，记∠AOC=θ．高．（Ⅰ）求sin2θ的值；（Ⅱ）若AB=7，求△BOC的面积．考点：二倍角的正弦；任意角的三角函数的定义．分析：（Ⅰ）先由三角函数定义求sinθ、cosθ，再根据正弦的倍角公式求出sin2θ；（Ⅱ）设点B坐标，然后列方程组解之，最后由三角形面积公式求得答案．解答：解：（Ⅰ）∵A点的坐标为（3，4），∴，∴，∴（Ⅱ）设B（x，y），由OB=3，AB=7得解得或，又点B在第二象限，故．∴△BOC的面积点评：本题考查三角函数定义、正弦的二倍角公式及方程思想．19．在等差数列{a n}中，a2+a7=﹣23，a3+a8=﹣29．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设数列{a n+b n}是首项为1，公比为c的等比数列，求{b n}的前n项和S n．考点：数列的求和；等差数列的通项公式．专题：计算题．分析：（Ⅰ）依题意 a3+a8﹣（a2+a7）=2d=﹣6，从而d=﹣3．由此能求出数列{a n}的通项公式．（Ⅱ）由数列{a n+b n}是首项为1，公比为c的等比数列，得，所以．所以=．由此能求出{b n}的前n项和S n．解答：（Ⅰ）解：设等差数列{a n}的公差是d．依题意 a3+a8﹣（a2+a7）=2d=﹣6，从而d=﹣3．所以 a2+a7=2a1+7d=﹣23，解得 a1=﹣1．所以数列{a n}的通项公式为 a n=﹣3n+2．（Ⅱ）解：由数列{a n+b n}是首项为1，公比为c的等比数列，得，即，所以．所以=．从而当c=1时，；当c≠1时，．点评：本题考查数列的通项公式和前n项和公式的求法，解题时要认真审题，仔细解答，注意合理地进行等价转化．20．如图所示，四棱锥P﹣ABCD的底面ABCD是直角梯形，BC∥AD，AB⊥AD，AB=BC=AD，PA⊥底面ABCD，过BC的平面交PD于M，交PA于N（M与D不重合）．（1）求证：MN∥BC；（2）如果BM⊥AC，求此时的值．考点：直线与平面垂直的性质；空间中直线与直线之间的位置关系．专题：证明题；空间位置关系与距离．分析：（1）根据线面平行的性质定理即可证明MN∥BC；（2）根据线面垂直的判定定理证明BCDK是平行四边形，即可证明M是PD的中点即可得到结论．解答：证明：（Ⅰ）∵BC∥AD，BC⊄平面PAD，AD⊂平面PAD，∴BC∥平面PAD，∵平面PAD∩平面BCMN=MN，∴BC∥MN，即MN∥BC；…（2）过M作MK∥PA交AD于K，连结BK．因为PA⊥底面ABCD，所以MK⊥底面ABCD．所以MK⊥AC．又因为BM⊥AC，BM∩MK=M，所以AC⊥平面BMK，所以AC⊥BK．由AC⊥CD，所以在平面ABCD中可得BCDK是平行四边形．所以BC=DK=AK，因为K是AD中点，所以M为PD中点．所以．…点评：本题主要考查线面垂直和线面平行的判定和性质，综合考查空间直线和平面的位置关系的判定，要求熟练掌握相应的判定定理和性质定理，考查学生的运算和推理能力，属于基本知识的考查．21．已知离心率为的椭圆的右焦点F是圆（x﹣1）2+y2=1的圆心，过椭圆上的动点P作圆的两条切线分别交y轴于M、N两点．（1）求椭圆的方程；（2）求线段MN长的最大值，并求此时点P的坐标．考点：直线与圆锥曲线的综合问题；椭圆的标准方程．专题：计算题；综合题．分析：（I）根据圆方程可求得圆心坐标，即椭圆的右焦点，根据椭圆的离心率进而求得a，最后根据a，b和c的关系求得b，则椭圆方程可得．（II）P（x0，y0），M（0，m），N（0，n），把椭圆方程与圆方程联立求得交点的横坐标，进而可推断x0的范围，把直线PM的方程化简，根据点到直线的距离公式表示出圆心到直线PM 和PN的距离．求得x0和y0的关系式，进而求得m+n和mn的表达式，进而求得|MN|．把点P代入椭圆方程根据弦长公式求得MN|．记，根据函数的导函数判断函数的单调性，进而确定函数f（x）的值域，进而求得当时，|MN|取得最大值，进而求得y0，则P点坐标可得．解答：解：（I）∵圆（x﹣1）2+y2=1的圆心是（1，0），∴椭圆的右焦点F（1，0），∵椭圆的离心率是，∴∴a2=2，b2=1，∴椭圆的方程是．（II）设P（x0，y0），M（0，m），N（0，n），由得，∴．直线PM的方程：，化简得（y0﹣m）x﹣x0y+x0m=0．又圆心（1，0）到直线PM的距离为1，∴，∴（y0﹣m）2+x02=（y0﹣m）2+2x0m（y0﹣m）+x02m2，化简得（x0﹣2）m2+2y0m﹣x0=0，同理有（x0﹣2）n2+2y0n﹣x0=0．∴，，∴=．∵P（x0，y0）是椭圆上的点，∴，∴，记，则，时，f'（x）＜0；时，f'（x）＜0，∴f（x）在上单调递减，在内也是单调递减，∴，当时，|MN|取得最大值，此时点P位置是椭圆的左顶点．点评：本题主要考查了直线与圆锥曲线的综合问题．考查考生分析问题、解决问题的能力．22．设函数f（x）=e x（lnx﹣a），e是自然对数的底数，e≈2.718…，a∈R且为常数．（1）若y=f（x）在x=1处的切线的斜率为2e，求a的值；（2）若y=f（x）在区间[ln2，ln3]上为单调函数，求a的取值范围．考点：利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．专题：导数的综合应用．分析：（1）对函数进行求导，由f'（1）=2e求得a（2）由[ln2，ln3]是y=f（x）的一个单调区间当且仅当f′（x）在[ln2，ln3]上恒大于等于零，或恒小于等于零．注意对对数h（ln2）和h（ln3）的大小比较有两种方法：方法一：利用作差法比较h（ln2）和h（ln3）的大小，方法二：构造新函数，利用新函数的单调性比较大小解答：解：（1）…依题意，k=f'（1）=e1（ln1﹣a+1）=2e，解得a=﹣1…（2），[ln2，ln3]是y=f（x）的一个单调区间．当且仅当f′（x）在[ln2，ln3]上恒大于等于零，或恒小于等于零，由e x＞0，作，，由得x=1…列表如下：x [ln2，1） 1 （1，ln3]h′（x）﹣0 +h（x）↘最小值↗…h（x）在[ln2，ln3]上的最小值为m=1，所以，当且仅当a≤1时，y=f（x）在[ln2，ln3]上单调递增…下面比较h（ln2）与h（ln3）的大小（方法一）由23＜32＜e3，，又h（x）在[ln2，1）上单调递减得……，∴h（ln2）＞h（ln3），当且仅当时，y=f（x）在[ln2，ln3]上单调递减，综上所述，a的取值范围为…（方法二）由，，以及的单调性知，…由知，单调递减…由ln3＞1得，，，∴h（ln2）＞h（ln3），当且仅当时，y=f（x）在[ln2，ln3]上单调递减，综上所述，a的取值范围为…（“单调递增…”以下，若直接写，再给1分）点评：本题主要考查导数的几何意义和导数在单调性中得应用和用其求参数范围的方法，属于难题．。

湖北省宜昌一中2015届高考物理二模试卷一、选择题〔共8小题，每一小题6分，总分为48分〕1．电子感应加速器根本原理如下列图，上、下为电磁铁两个磁极，磁极之间有一个环形真空室，电子在真空中做圆周运动．电磁铁线圈电流的大小、方向可以变化．甲图为侧视图，乙图为真空室的俯视图，假设某一时刻，电磁铁线圈电流方向与图示方向一致、电子正沿逆时针方向作加速运动，如此如下说法正确的答案是( )A．电子感应加速器是利用磁场对电子的洛伦兹力作用使电子加速的B．电子感应加速器是利用感生电场使电子加速的C．电磁铁线圈中电流大小要保持恒定D．此时真空室中的感生电场沿逆时针方向2．如下列图是研究影响平行板电容器的电容大小的因素的实验电路．平行板电容器充电后，将极板A与一灵敏静电计的金属小球相接，极板B接地，静电计金属外壳接地，假设极板B 稍向上移动一点，由观察到的静电计指针变化做出平行板电容器电容变小结论的依据是( )A．两极板间的电压不变，极板上的电荷量变大B．两极板间的电压不变，极板上的电荷量减小C．极板上的电荷量几乎不变，两极板间的电压变大D．极板上的电荷量几乎不变，两极板间的电压变小3．如下列图，将质量为m=0.1kg的物体用两个完全一样的竖直弹簧固定在升降机内，当升降机以4m/s2的加速度加速向上运动时，上面弹簧对物体的拉力为0.4N；当升降机和物体都以8m/s2的加速度向上运动时，上面弹簧的拉力为( )A．0.6N B．0.8N C．1.0N D．1.2N4．一理想变压器原、副线圈的匝数比为44：1，原线圈输入电压的变化规律如图甲所示，副线圈所接电路如图乙所示，P为滑动变阻器的触头．如下说法正确的( )A．副线圈输出电压的频率为100HzB．副线圈输出电压的有效值为5VC．P向左移动时，变压器原、副线圈的电流都减小D．P向左移动时，变压器的输入功率增加5．经长期观测发现，A行星运行的轨道半径为R0，周期为T0，但其实际运行的轨道与圆轨道总存在一些偏离，且周期性地每隔t0时间发生一次最大的偏离．如下列图，天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B，如此行星B运动轨道半径R( )A．R=R0B．R=R0C．R=R0D．R=R06．如图，平行板电容器两个极板与水平地面成2α角，在平行板间存在着匀强电场，直线CD是两板间一条垂直于板的直线，竖直线EF与CD交于O点，一个带电小球沿着∠FOD的角平分线从A点经O点向B点做直线运动，重力加速度为g．如此在此过程中，如下说法正确的答案是( )A．小球可能带正电，也可能带负电B．小球可能做匀加速直线运动C．小球加速度大小为gcosαD．小球重力势能的增加量等于电势能的增加量7．如下列图，在方向竖直向下、磁感应强度大小为B的匀强磁场中有一水平放置的半圆形轻质导体框，O为圆心，圆半径长为L，AO段、BO段导体的电阻可忽略，圆弧AB段的电阻为r，半圆直径与磁场边界重合；现用外力使导体框从图示位置开始绕过O、垂直于半圆面的轴以角速度ω沿逆时针方向匀速转动一周，如下分析正确的答案是( )A．圆弧AB段内电流方向总是从A流向BB．转动的前半周内AB两端电压为C．转动的后半周内通过O点的电量为D．外力对线框做的功为8．一质量为m的小球以初动能E k0从地面竖直向上抛出，上升过程中受到阻力f作用，如下列图，图中两条图线分别表示小球在上升过程中动能、重力势能中的某一个与其上升高度之间的关系，〔以地面为零势能面，h0表示上升的最大高度，图上坐标数据中的k为常数且满足0＜k＜1〕如此由图可知，如下结论正确的答案是( )A．①、②分别表示的是动能、重力势能随上升高度的图象B．上升过程中阻力大小恒定且f=kmgC．上升高度h=h0时，重力势能和动能相等D．上升高度h=时，动能与重力势能之差为mgh0三、非选择题：包括必考题和选考题两局部．第9题～第12题为必考题，每个试题考生都必须作答．第13题～第16题为选考题，考生根据要求作答．〔一〕必考题9．在探究“加速度与力的关系〞实验中，某同学设计了一种新的方法：他按如图1所示安装好实验装置，在不悬挂小吊盘时，调整木板右端的高度，用手轻拨小车，使小车能牵引纸带沿长木板向左做匀速运动．然后将一定数量的砝码〔其总质量为m〕放入小吊盘中〔小吊盘质量不计〕，接通电源，释放小车，打出一条理想纸带，并在纸带上标出小吊盘中砝码所受的重力F．以后每次实验将小吊盘中局部砝码移到小车中，保持砝码和小车的总质量一定，重复实验屡次，并计算出每条纸带对应的加速度．回答如下问题：〔1〕按上述方案做实验，是否要求小吊盘中砝码的总质量远小于小车的质量？__________〔填“是〞或“否〞〕〔2〕该同学以每次实验中小吊盘中砝码所受的重力F为横坐标，小车对应的加速度大小a 为纵坐标，在坐标纸上作出a﹣F关系图线．图2图线中，你认为合理的是__________ 〔3〕假设该同学所作出a﹣F关系图线，直线〔或直线局部〕斜率为k，如此小车质量M=__________．10．为了测定一节干电池的电动势和内阻，实验室提供了如下器材：A．待测干电池〔电动势1.5V左右，内阻不超过1.5Ω〕B．电流表A1〔量程0～2mA，内阻R A1=10Ω〕C．电流表A2〔量程0～0.6A，内阻约为0.1Ω〕D．滑动变阻器R1〔0～20Ω，10A〕E．滑动变阻器R2〔0～100Ω，1A〕F．定值电阻R3=990ΩG．开关、导线假设干利用以上提供的器材，欲测量该电池的电动势和内阻，请回答以下问题：〔1〕为测量方便且测量误差较小，上述滑动变阻器应选用__________〔填写序号字母〕．〔2〕在图1所示虚线框内补画出完整的电路原理图．〔3〕根据合理的设计电路测量数据，电流表A1的示数记为I1，电流表A2的示数记为I2，某同学测出了6组I1、I2的数据，如表所示．在图2坐标纸上作出I1和I2的关系图线．根据描绘出的图线，可得被测电池的电动势为__________V，内阻为__________Ω．〔计算结果保存两位小数〕11．两小孩在平直跑道上做游戏，各自用不同的水平恒力使质量m=10kg的一样物体甲、乙从起跑线由静止开始运动．水平恒力F1=50N持续作用t1=3s使甲运动到离起跑线x=18m处；水平恒力F2=30N持续在乙上作用t2=5s后撤去，求：〔1〕物体受到的阻力；〔2〕乙物体最后停在离起跑线多远处．12．如下列图，半径为R的圆形区域，c为圆心，在圆上a点有一粒子源以一样的速率向圆面内各个方向发射多个质量为m、电荷量为+q 的带电粒子．当圆形区域存在垂直于圆面、磁感应强度大小为B的匀强磁场时，沿ac方向射入的粒子从b 点离开场区，此过程粒子速度方向偏转了．假设只将圆形区域内的磁场换成平行于圆面的匀强电场，粒子从电场圆边界的不同位置射出时有不同的动能，其最大动能是初动能的4倍，经过b点的粒子在 b 点的动能是初动能的3倍．不计粒子重力与粒子间的相互作用．求：〔1〕粒子源发射粒子的速率v0与从b点离开磁场的粒子在磁场中运动的最长时间t m〔2〕电场强度的方向与大小．〔二〕选考题，请考生从以下2个模块中任选一模块作答[物理--选修3-4]13．一列简谐横波沿x轴正方向传播，t时刻波形图如图中的实线所示，此时波刚好传到P 点，t+0.6s时刻的波形如图中的虚线所示，a、b、c、P、Q是介质中的质点，如此以下说法正确的答案是( )A．这列波的波速可能为50m/sB．从t+0.6 s时刻开始，经过0.5T，质点b沿x轴正方向运动20mC．质点c在这段时间内通过的路程可能为60 cmD．假设T=0.8s，如此当t+0.5s时刻，质点b、P的位移一样E．假设T=0.8s，当t+0.4s时刻开始计时，如此质点c的振动方程为y=0.1sin〔πt〕〔m〕14．在真空中有一正方体玻璃砖，其截面如下列图，它的边长为d．在AB面上方有一单色点光源S，从S发出的光线SP以60°入射角从AB面中点射入，当它从侧面AD射出时，出射光线偏离入射光线SP的偏向角为30°，假设光从光源S到AB面上P点的传播时间和它在玻璃砖中传播的时间相等，求点光源S到P点的距离．[物理--选修3-5]15．如图为氢原子的能级示意图，锌的逸出功是3.34ev，那么对氢原子在能级跃迁过程中发射或吸收光子的规律认识正确的答案是( )A．用氢原子从高能级向基态跃迁时发射的光照射锌板一定不能产生光电效应B．一群处于n=4能级的氢原子向低能级跃迁所辐射的光中，有3种不同频率的光能使锌发生光电效应C．一群处于n=3能级的氢原子向基态跃迁时，发出的光照射锌板，锌板外表所发出的光电子的最大初动能为8.75eVD．用能量为10.21eV 的光子照射，可使处于基态的氢原子跃迁到激发态E．用能量为14.0eV的光子照射，可使处于基态的氢原子电离16．如下列图，在固定的光滑水平杆〔杆足够长〕上，套有一个质量为m=0.5kg的光滑金属圆环，轻绳一端拴在环上，另一端系着一个质量为M=1.98kg的木块，现有一质量为m0=20g 的子弹以v0=100m/s的水平速度射入木块并留在木块中〔不计空气阻力和子弹与木块作用的时间，g取10m/s2〕，求：①圆环、木块和子弹这个系统损失的机械能；②木块所能达到的最大高度．湖北省宜昌一中2015届高考物理二模试卷一、选择题〔共8小题，每一小题6分，总分为48分〕1．电子感应加速器根本原理如下列图，上、下为电磁铁两个磁极，磁极之间有一个环形真空室，电子在真空中做圆周运动．电磁铁线圈电流的大小、方向可以变化．甲图为侧视图，乙图为真空室的俯视图，假设某一时刻，电磁铁线圈电流方向与图示方向一致、电子正沿逆时针方向作加速运动，如此如下说法正确的答案是( )A．电子感应加速器是利用磁场对电子的洛伦兹力作用使电子加速的B．电子感应加速器是利用感生电场使电子加速的C．电磁铁线圈中电流大小要保持恒定D．此时真空室中的感生电场沿逆时针方向考点：质谱仪和盘旋加速器的工作原理．分析：根据右手螺旋定如此，结合电磁波理论，如此可磁场发生变化，通过楞次定律可判断出涡旋电场的方向，从而可知电子在涡旋电场下的运动．解答：解：ABD、当电磁铁中应通以方向如图甲所示，大小增强的电流，线圈中的磁场就增大了，根据楞次定律，感生电场产生的磁场要阻碍它增大所以感生电场俯视图为顺时针方向，所以电子运动逆时针方向电场力作用下加速运动，在洛伦兹力约束下做圆周运动，故AD错误，B正确．C、由上分析可知，当线圈中电流大小要保持恒定时，不会激发出感生电场，故D错误；应当选：B．点评：解决此题的关键掌握楞次定律判断感应电流的方向，感应电流的磁场总是阻碍引起感应电流磁场磁通量的变化．2．如下列图是研究影响平行板电容器的电容大小的因素的实验电路．平行板电容器充电后，将极板A与一灵敏静电计的金属小球相接，极板B接地，静电计金属外壳接地，假设极板B 稍向上移动一点，由观察到的静电计指针变化做出平行板电容器电容变小结论的依据是( )A．两极板间的电压不变，极板上的电荷量变大B．两极板间的电压不变，极板上的电荷量减小C．极板上的电荷量几乎不变，两极板间的电压变大D．极板上的电荷量几乎不变，两极板间的电压变小考点：电容．专题：电容器专题．分析：电容器与电源断开，电量不变，根据决定式判断电容的变化，静电计测量的是两极板间的电势差，根据定义式判断两板间电压的变化．解答：解：根据C=知，极板B稍向上移动一点，s减小，如此电容变小，根据C=知，极板上的电荷量几乎不变，两板间的电压变大，故C正确，ABD错误．应当选：C．点评：考查电容表达式，解决此题的关键掌握电容的决定式C=和电容的定义式C=的综合应用．3．如下列图，将质量为m=0.1kg的物体用两个完全一样的竖直弹簧固定在升降机内，当升降机以4m/s2的加速度加速向上运动时，上面弹簧对物体的拉力为0.4N；当升降机和物体都以8m/s2的加速度向上运动时，上面弹簧的拉力为( )A．0.6N B．0.8N C．1.0N D．1.2N考点：牛顿第二定律；胡克定律．专题：牛顿运动定律综合专题．分析：根据牛顿第二定律求出升降机以4m/s2的加速度加速向上运动时，下面弹簧的弹力．然后根据牛顿第二定律求出升降机和物体都以8m/s2的加速度向上运动时，上面弹簧的拉力．解答：解：当升降机以4m/s2的加速度加速向上运动时，设下面弹簧处于压缩，根据牛顿第二定律得，F1+F2﹣mg=ma1，F2=1.0N．当升降机和物体都以8m/s2的加速度向上运动时，合力F合=ma2=0.8N，根据牛顿第二定律知，两根弹簧作用在物体上的合力为1.8N，如此物块要下移，根据胡克定律，两根弹簧增加的弹力相等，开始F1=0.4N，F2=1.0N，如此每根弹簧增加0.2N，所以上面弹簧的弹力为0.6N．故A正确，B、C、D错误．应当选A．点评：解决此题的关键掌握牛顿第二定律以与胡克定律，知道物体下移时，两根弹簧的形变量相等，弹力变化相等．4．一理想变压器原、副线圈的匝数比为44：1，原线圈输入电压的变化规律如图甲所示，副线圈所接电路如图乙所示，P为滑动变阻器的触头．如下说法正确的( )A．副线圈输出电压的频率为100HzB．副线圈输出电压的有效值为5VC．P向左移动时，变压器原、副线圈的电流都减小D．P向左移动时，变压器的输入功率增加考点：变压器的构造和原理．专题：交流电专题．分析：根据瞬时值表达式可以求得输出电压的有效值、周期和频率等，再根据电压与匝数成正比即可求得结论解答：A、由图象可知，交流电的周期为0.02s，所以交流电的频率为50Hz，所以A错误．B、根据电压与匝数成正比可知，原线圈的电压的最大值为220V，所以副线圈的电压的最大值为5V，所以电压的有效值为V==5V，所以B错误．C、P左移，R变大，副线的电压不变，如此副线圈的电流变小，原线圈的电流也随之变小，故C正确．D、P向左移动时，滑动变阻器的电阻变大，副线圈的电压不变，所以电路消耗的功率将变小，变压器的输入功率等于输出功率都变小，故D错误．应当选：C点评：电路的动态变化的分析，总的原如此就是由局部电路的变化确定总电路的变化的情况，再确定其他的电路5．经长期观测发现，A行星运行的轨道半径为R0，周期为T0，但其实际运行的轨道与圆轨道总存在一些偏离，且周期性地每隔t0时间发生一次最大的偏离．如下列图，天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B，如此行星B运动轨道半径R( )A．R=R0B．R=R0C．R=R0D．R=R0考点：开普勒定律．专题：万有引力定律的应用专题．分析：先根据多转动一圈时间为t0，求出卫星的周期；然后再根据开普勒第三定律解得轨道半径．解答：解：A行星发生最大偏离时，A、B行星与恒星在同一直线上且位于恒星同一侧，设行星B的运行周期为T、半径为R，如此有：t0﹣t0=2π，所以T=，由开普勒第三定律得：=，解得：R=R0，应当选：A．点评：从此题可以看出，通过测量环绕天体的轨道半径和公转周期，可以求出中心天体的质量．6．如图，平行板电容器两个极板与水平地面成2α角，在平行板间存在着匀强电场，直线CD是两板间一条垂直于板的直线，竖直线EF与CD交于O点，一个带电小球沿着∠FO D的角平分线从A点经O点向B点做直线运动，重力加速度为g．如此在此过程中，如下说法正确的答案是( )A．小球可能带正电，也可能带负电B．小球可能做匀加速直线运动C．小球加速度大小为gcosαD．小球重力势能的增加量等于电势能的增加量考点：匀强电场中电势差和电场强度的关系．专题：电场力与电势的性质专题．分析：首先以知道题境，以小球为研究对象，据运动情况判断小球的合外力的方向，在判断小球的电场力情况；再从功能关系的角度，据此分析判断选项即可．解答：解；A、一个带电小球沿着∠FOD的角平分线从A点经O点向B点做直线运动，所以小球合外力沿着AB；又由于小球受重力，所以电场力的方向由O到D；由于此电场的方向未知，所以小球的电量不确定，故A正确；B、据以上分析可知，小球做匀减速直线运动，故B错误；C、据图可知，由于是角平分线，且小球的加速度方向由O到D，据几何关系可知，a=2gcosα，故C错误；D、由以上分析可知，小球受重力等于电场力，运动的位移和夹角一样，所以二力做的功一样，据功能关系可知，小球重力势能的增加量等于电势能的增加量，故D正确．应当选：AD点评：此题难度较大，解题的突破口是找出重力和电场力的关系，在灵活应用几何关系和重力做功与电场力做功与势能的关系判断．7．如下列图，在方向竖直向下、磁感应强度大小为B的匀强磁场中有一水平放置的半圆形轻质导体框，O为圆心，圆半径长为L，AO段、BO段导体的电阻可忽略，圆弧AB段的电阻为r，半圆直径与磁场边界重合；现用外力使导体框从图示位置开始绕过O、垂直于半圆面的轴以角速度ω沿逆时针方向匀速转动一周，如下分析正确的答案是( )A．圆弧AB段内电流方向总是从A流向BB．转动的前半周内AB两端电压为C．转动的后半周内通过O点的电量为D．外力对线框做的功为考点：导体切割磁感线时的感应电动势；电磁感应中的能量转化．专题：电磁感应——功能问题．分析：分析导线的转动，根据右手定如此可明确电流的方向；根据旋转切割产生的电动势的表达式与欧姆定律可求得电压；由功能关系可求出外力所做的功．解答：解：A、在转动的前半周内，有效切割的局部为OB，由右手定如此可知，电流由B 到A；后面周期内切割的有效长度为AO，如此电流为由A流向B；故A错误；B、转动的前半周期内，由于AB电阻不计，圆弧上的电压即为电源的电动势，切割产生的电动势E=BL2ω；故B正确；C、转动的后面周期，磁通量的变化量△Φ=B；故电量Q==；故C错误；D、外力做功等于产生的电能，如此做功W=I2rt=〔〕2r×=；故D正确；应当选：BD．点评：此题考查导体旋转切割磁感线的电动势与电路规律的应用，要注意正确分析电路结构，明确功能关系的应用即可求解．8．一质量为m的小球以初动能E k0从地面竖直向上抛出，上升过程中受到阻力f作用，如下列图，图中两条图线分别表示小球在上升过程中动能、重力势能中的某一个与其上升高度之间的关系，〔以地面为零势能面，h0表示上升的最大高度，图上坐标数据中的k为常数且满足0＜k＜1〕如此由图可知，如下结论正确的答案是( )A．①、②分别表示的是动能、重力势能随上升高度的图象B．上升过程中阻力大小恒定且f=kmgC．上升高度h=h0时，重力势能和动能相等D．上升高度h=时，动能与重力势能之差为mgh0考点：动能定理的应用；重力势能的变化与重力做功的关系；功能关系．专题：动能定理的应用专题．分析：〔1〕动能大小的影响因素：质量、速度．质量越大，速度越大，动能越大．〔2〕重力势能大小的影响因素：质量、被举得高度．质量越大，高度越高，重力势能越大．〔3〕机械能=动能+势能．物体没有发生弹性形变时，不考虑弹性势能．解答：解：A、根据动能定理可知上升高度越大，动能越小，重力势能越大，故①、②分别表示重力势能、动能随上升高度的图象，故A错误；B、从②图线看，重力势能、动能随着高度的变化成线性关系，故合力恒定，受到的阻力大小恒定，由功能关系可知从抛出到最高点的过程中机械能的减少量等于阻力的功的大小，由②图线可知：fh0=E k0﹣，且由①图线根据动能定理可知E k0=〔mg+f〕h0，解得f=kmg，故B正确；C、设h高度时重力势能和动能相等，①图线的函数方程为E k=E k0﹣〔mg+f〕h，②图线的函数方程为E P=h，令E k=E P，与E k0=〔mg+f〕h0和f=kmg，联立解得h=h0，C正确；同理可得D正确应当选BCD点评：〔1〕掌握动能和重力势能大小的影响因素，根据图象能确定动能和势能的大小．〔2〕根据“E=E K+E P〞计算机械能的大小．三、非选择题：包括必考题和选考题两局部．第9题～第12题为必考题，每个试题考生都必须作答．第13题～第16题为选考题，考生根据要求作答．〔一〕必考题9．在探究“加速度与力的关系〞实验中，某同学设计了一种新的方法：他按如图1所示安装好实验装置，在不悬挂小吊盘时，调整木板右端的高度，用手轻拨小车，使小车能牵引纸带沿长木板向左做匀速运动．然后将一定数量的砝码〔其总质量为m〕放入小吊盘中〔小吊盘质量不计〕，接通电源，释放小车，打出一条理想纸带，并在纸带上标出小吊盘中砝码所受的重力F．以后每次实验将小吊盘中局部砝码移到小车中，保持砝码和小车的总质量一定，重复实验屡次，并计算出每条纸带对应的加速度．回答如下问题：〔1〕按上述方案做实验，是否要求小吊盘中砝码的总质量远小于小车的质量？否〔填“是〞或“否〞〕〔2〕该同学以每次实验中小吊盘中砝码所受的重力F为横坐标，小车对应的加速度大小a 为纵坐标，在坐标纸上作出a﹣F关系图线．图2图线中，你认为合理的是D〔3〕假设该同学所作出a﹣F关系图线，直线〔或直线局部〕斜率为k，如此小车质量M=．考点：探究加速度与物体质量、物体受力的关系．专题：实验题．分析：〔1〕把砝码和小车整体看成研究对象，根据牛顿第二定律分析即可求解；〔2、3〕根据牛顿第二定律求出加速度的表达式，分析a与F的关系，从而选择图象，并根据图象斜率的含义求出小车质量M．解答：解：〔1〕把砝码和小车整体看成研究对象，根据牛顿第二定律可知：mg=〔m+M〕a，假设把小吊盘中局部砝码移到小车中，保持砝码和小车的总质量一定，如此有：〔m﹣m0〕g=〔m+M〕a，我们发现不需要用砝码的重力代替绳子的拉力，用整体法求出的加速度就是小车的加速度，所以不需要砝码和砝码盘的总质量远小于小车的质量．〔2〕根据牛顿第二定律可知：F=〔m+M〕a，解得：a=如此加速度与F成正比，图象是通过原点的倾斜的直线，故D正确．应当选：D〔3〕a﹣F图象的斜率k=解得：M=故答案为〔1〕否；〔2〕D；〔3〕点评：对于实验题要掌握其原理，知道课本上的实验为什么要求重物的质量远远小于小车的质量，能根据牛顿第二定律求出加速度与F的关系，知道a﹣F图象斜率的含义，题目比拟新颖，难度适中．10．为了测定一节干电池的电动势和内阻，实验室提供了如下器材：A．待测干电池〔电动势1.5V左右，内阻不超过1.5Ω〕B．电流表A1〔量程0～2mA，内阻R A1=10Ω〕C．电流表A2〔量程0～0.6A，内阻约为0.1Ω〕D．滑动变阻器R1〔0～20Ω，10A〕E．滑动变阻器R2〔0～100Ω，1A〕F．定值电阻R3=990ΩG．开关、导线假设干利用以上提供的器材，欲测量该电池的电动势和内阻，请回答以下问题：〔1〕为测量方便且测量误差较小，上述滑动变阻器应选用D〔填写序号字母〕．〔2〕在图1所示虚线框内补画出完整的电路原理图．。

宜昌一中2015年高考适应性考试（二）数 学（理工类）本试卷4页，共22题，其中第15、16题为选考题。

满分150分。

考试用时120分钟。

★祝考试顺利★一、选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集U ＝R ，{}|1A x x =<，{}|2B y x y =-+=，则集合∁U （A ∪B ）＝( )A ．{}|12x x ≤<B ．{}|12x x <≤C ．{}|1x x ≥D ．{}|2x x ≤2.已知i 为虚数单位，R a ∈，若ia i+-2为纯虚数，则复数i a z 2)12(++=的模等于（ ） A ．2 B ．3 C ．11 D ．6 3.()sin()(0,0)f x A x A ωϕω=+>>在1x =处取得极大值，则（ ） A ．(1)f x -一定是奇函数 B ．(1)f x -一定是偶函数 C ．(1)f x +一定是奇函数 D ．(1)f x +一定是偶函数4.一个几何体的三视图如图所示，正视图和侧视图都是等边三角形。

若 该几何体的四个顶点在空间直角坐标系O xyz -中的坐标分别是（0，0，0）， （2，0，0），（2，2，0），（0，2，0），则第五个顶点的坐标可能为( ) A ．（1，1，1） B ．（1，1C ．（1，1D ．（2，25．已知MOD 函数是一个求余函数，其格式为(,)MOD n m ，其结果为n 除以m 的余数，例如(8,3)2MOD =. 下面是一个算法的程序框图，当输入的值为36时，则输出的结果为（ ）.A ．7B ．5C ．6D ．46.现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率：先由计算器给出0到9之间取整数值的随机数，指定0，1表示没有击中目标，2，3，4，5，6，7，8，9表示击中目标，以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:7527 0293 7140 9857 0347 4373 8636 6947 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281 根据以上数据估计该射击运动员射击4次至少击中3次的概率为( ) A ．0.852 B ．0.8192 C ．0.8 D ．0.757.已知,x y 满足约束条件133x x y ay x ≥⎧⎪+≤⎨⎪≥-⎩,若2xz y =+的最小值为1,则实数a 的值是 ( )A.4B.12C. 2D. 1 8.对任意正数,x y ，不等式333x yk x y x y+≤++恒成立，则实数k 的取值范围是（ ）正视图 侧视图俯视图A ．5,4⎡⎫+∞⎪⎢⎣⎭B．⎫+∞⎪⎪⎣⎭ C ．[)1,+∞ D．⎫+∞⎪⎪⎣⎭9.已知椭圆:C 22221x y a b+=（0a b >>）的左右顶点分别为A ，B ，左右焦点分别为1F ，2F ，点O 为坐标原点，线段OB 的中垂线与椭圆在第一象限的交点为P ，设直线PA ，PB ，1PF ，2PF 的斜率分别为1k ，2k ，3k ，4k ，若1214k k ⋅=-，则34k k ⋅=( )AB ．83-C ．38-D ．4-10.已知函数⎪⎩⎪⎨⎧>-≤-+=0),1(0,11)(x x f x x x x f ,则函数a e x f x g x +-=)()(的零点个数不可能是（ ）A ．3B ． 0C ．2D ．1二、填空题：本大题共6小题，考生共需作答5小题，每小题5分，共25分. 请 将答案填在答题卡对应题号．．．．．．．的位置上. 答错位置，书写不清，模棱两可均不得分. （一）必考题（11—14题）11.若(1,1),(2,)a b x →→=-=，且a →在()a b →→-上的投影为1-，则x = 12.已知a ＞0，(x –2x a )6的二项展开式中，常数项等于60，则(x –2xa )6的展开式中各项系数之和为 （用数字作答）． 13.1与两坐标轴所围成图形的面积是14.图中的三角形称为希尔宾斯三角形，在下列四个三角形中，黑色三角形的个数依次构成数列{}n a 的前四项，依此着色方案继续对三角形着色.（1）数列{}n a 的通项公式n a =_____________；（2）若数列{}n b 满足12()3nn n b a +=⋅，记01232020202012022019M C C C b C b C b =+++⋅++⋅，则M 的个位数字是_________．（二）选考题（请考生在第15、16两题中任选一题作答，请先在答题卡指定位置将你所选的题目序号后的方框用2B 铅笔涂黑. 如果全选，则按第15题作答结果计分.）15.（选修4-1：几何证明选讲）如图,在圆O 中,直径AB 与弦CD 垂直,垂足为E ,EF ⊥DB ,垂足为F ,若AB =6,AE =1,则DF ·DB =________16. （选修4-4：坐标系与参数方程）已知曲线C 的参数方程为,,x t y t ⎧=⎪⎨=⎪⎩（t 为参数），C 在点(1,1)处的切线为l ，以坐标原点为极点，x 轴的正半轴为极轴 建立极坐标系，则l 的极坐标方程为三、解答题：本大题共6小题，共75分. 解答应写出必要的文字说明、证明过…程或演算步骤.17.（本小题满分12分）在等比数列{}n a 中，其前n 项和为n S ,已知233=a ,293=S . （I ）求数列{}n a 的通项公式；（II ）是否存在正整数n ，使得3232=-+n n S S 成立，若存在，求出n 的值，若不存在，请说明理由.18.（本小题满分12分）在△ ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且212cos cos sin()sin cos()22A B B A B B A C ---++=-(Ⅰ)求A ；(Ⅱ)D 为边BC 上一点，BD =3DC ，∠DAB=π2，求tan C ．19.（本小题满分12分）在如图4所示的几何体中，四边形ABCD 为平行四边形，平面AEC ⊥平面ABCD ，90ACB ∠=︒，EF ∥BC ，BC EF 21=，2==BC AC ，EC AE =． （Ⅰ）求证：CF AF =．（Ⅱ）当二面角D EC A --的平面角的余弦值为33时，求三棱锥A EFC -的体积．20.（本小题满分12分）某通讯设备每台的销售利润与该设备的无故障使用时间Q(单位：年)有关，若Q ≤1,AB DC EF图4则销售利润为0元；若1<Q ≤3，则销售利润为10万元；若Q >3,则销售利润为20万元.已知 每台该种设备的无故障使用时间为Q ≤1,1<Q ≤3及Q >3这三种情况发生的概率分别p 1,p 2,p 3,又知p 1, p 2是方程25x 2-15x +a =0的两个根，且p 2=p 3. (Ⅰ)求a 的值；(Ⅱ)记两台这种设备的销售利润之和为ξ，求ξ的分布列和期望.21.（本小题满分13分）如图，抛物线1C ：px y 22=与椭圆2C ：1121622=+y x 在第一象限的交点为B ，O 为坐标原点，A 为椭圆的右顶点，OAB ∆的面积为368.（Ⅰ）求抛物线1C 的方程；（Ⅱ）过A 点作直线l 交1C 于C 、D 两点，射线OC 、OD 分别交2C 于E 、F 两点，记 OEF ∆和OCD ∆的面积分别为1S 和2S ，问是否存在直线l ，使得77:3:21=S S ？若存在， 求出直线l 的方程；若不存在，请说明理由．22.（本小题满分14分）已知函数()()2*21n nx axf x n N x -=∈+的图象在点()()0,0n f 处的切线方程为y x =-. (Ⅰ)求a 的值及1()f x 的单调区间(Ⅱ)是否存在实数k ，使得射线()3y kx x =≥-与曲线()1y f x =有三个公共点？若存 在，求出k 的取值范围；若不存在，说明理由 (Ⅲ)设12,,n x x x ，为正实数，且121n x x x +++=L ，证明：()()()120n n n n f x f x f x +++≥宜昌一中2015年高考适应性考试（二）数学（理）评 分 标 准17.（1）设等差数列的公比为q ，依题意，有212a q =，21112a a q a q ++=…………2分解得13,12a q ==或116,2a q ==-………………4分故数列{}n a 的通项公式为32n a =或1162n n a -⎛⎫=⋅- ⎪⎝⎭………………6分（2）①当13,12a q ==时，由3232=-+n n S S 333(2)2232n n ⇒-+=，无解 ………………7分 ②当116,2a q ==-时，141()2n n S ⎡⎤=--⎢⎥⎣⎦， 由3232=-+n n S S 11()5232n n ⇒-=-⇒= ……………11分 综合①②知，存在比为5n =，使得3232=-+n n S S 成立 ……………12分18.（Ⅰ）（过程略）A ＝2π3． …5分（Ⅱ）因为∠DAB ＝ π 2，所以AD ＝BD ·sin B ，∠DAC ＝ π 6． 在△ACD 中，有ADsin C＝CDsin ∠DAC，又因为BD ＝3CD ，所以3sin B ＝2sin C ，由B ＝ π 3－C 得332cos C －32sin C ＝2sin C ，整理得tan C ＝337．…12分19．（Ⅰ）证明：因为90=∠ACB ，平面AEC 平面ABCD ，所以⊥BC 平面AEC ,又EF ∥BC ，所以⊥EF 平面AEC ，所以CE EF AE EF ⊥⊥,,又EC AE =，所以CEF ∆≌AEF ∆,∴CF AF =； ………………………………………………5分（Ⅱ）取AC 的中点O ，因为EC AE =，所以AC EO ⊥,又平面AEC 平面ABCD ， 所以⊥EO 平面ABCD , …………………………………………………6分 如图建立空间直角坐标系，则)0,0,1(C ，)0,0,1(-A ，)0,2,1(-D ,设),0,0(m EB D),2,1(),,0,1(m m --=-=∴，设平面ECD 的法向量为(1x n =则由⎪⎩⎪⎨⎧=⋅=⋅011n EC n ,即⎩⎨⎧=-+-=-020m y x m x ，得m y m x ==,)1,,(1m m n =∴ 由（Ⅰ）知⊥EF 平面AEC ，所以平面AEC 量为2(0,1,0)n FE ==,121212cos ,||||2n n n n n n ⋅∴<>===，1=∴m ,所以13A EFC F AEC ACE V V EF S --∆==⋅111112323=⨯⨯⨯⨯= ………………12分 20．解： (1)由已知得p 1+p 2+p 3=1,∵p 2=p 3,∴p 1+2p 2=1. ∵p 1,p 2是方程25x 2-15x+a=0的两个根，∴1212312p p ,p ,p .555+=∴== 12225p p ∴= 故a=2 …………4分 (2)ξ的可能取值为0,10,20,30,40. P(ξ=0)=111,5525⨯=P(ξ=10)=12425525⨯⨯=, P(ξ=20)=122282,555525⨯⨯+⨯=P(ξ=30)=2282,5525⨯⨯=P(ξ=40)=224.5525⨯= 随机变量ξ的分布列为:E(ξ)= 010********.2525252525⨯+⨯+⨯+⨯+⨯=…………………12分 21. 解: (Ⅰ)因为OAB ∆的面积为368,所以364=B y ，代入椭圆方程得)364,34(B ， 抛物线的方程是：x y 82= (Ⅱ) 解：显然直线l 不垂直于y 轴，故直线l 的方程可设为4x my =+，与x y 82=联立得03282=--my y .设),(),,(2211y x D y x C ,则32,82121-=⋅=+y y m y y 12211sin 21sin 2E FOC OD COD OC OD y y S S OE OF y y OE OF EOF ∠∴===∠F E y y 32=,由直线OC 的斜率1118y x y =,故直线OC 的方程为x y y 18=，与1121622=+y x 联立得1)1211664(212=+⋅y y E ，同理1)1211664(222=+⋅y y F ，所以2E y ⋅1)1211664)(1211664(22212=+⋅+⋅y y y F………8分 可得2E y ⋅223625612148F y m ⨯=+要使37712=S S ，只需22232(12148)77362563m +⎛⎫= ⎪⨯⎝⎭………10分即21214849121m +=⨯,解得11±=m ，………12分所以存在直线l : 0411=-±y x 21. 解：（Ⅰ）因为22()1n nx axf x x -=+， 所以()()()()()2222212()1n nx a x nx ax x f x x -+--¢==+因为曲线()n y f x =在点()()0,0n f 处切线方程为y=-x,所以(0)1n f ¢=-， 即11a a-=-?. 于是()22221()1n x nx f x x+-¢=+.由1()0f x ¢>，即()2222101x x x +->+，解得1,x <-或1x >-+；由1()0f x ¢<，即()2222101x x x+-<+，解得11x --<<-+1()f x 的递增区间为((),1,1-?--++?；递减区间为(11---+ .……………… 5分（Ⅱ）由221x x y x y kx ìï-ï=ïí+ïï=ïïî，消去y 得221x x kx x -=+，即x=0或211x k x -=+. 要使射线y=kx(3x ?)与曲线1()y f x =有三个交点，只要方程211x k x -=+，即210kx x k -++=有两个大于或等于-3且不等于0的不等实根.1. 当k=0 时，210kx x k -++=可化为-x+1=0,解得x=1,不符合要求； 2. 当k ≠0时，令2()1g x kx x k =-++.由()()30000132kg g k ìï-?ïïïï¹ïïíD >ïïïïï>-ïïî，即(104)01014(1)0132k k k k k k ìï+?ïïï+?ïïïí-+>ïïïï?-ïïî，即205116k k k k k k ìïï??ïïïï?ïïïíï<<ïïïïïï<->ïïî或或解得1120,225k k -+--<<<?或且1k ?.综上，存在实数k 使得射线y=kx(3x ?)与曲线1()y f x =有三个交点，且k 的取值范围是12111,0,252骣骣纟--?+珑ç鼢ú珑---ç鼢珑鼢çúç珑鼢è珑桫桫ûU U ..…………… 9分 (Ⅲ)证明：因为22()1n nx x f x x -=+，()22221()1n x nx f x x +-¢=+， 所以1()0n f n =，221()1n n f n n ¢=+.所以曲线()n y f x =在点11,n f n n 骣骣÷琪ç÷÷çç÷÷ç÷÷çç桫桫处的切线方程为2211n y x nn 骣÷ç÷=-ç÷ç÷+桫.当0<x<1时， ()()()()222222222111()011111n n x nx n nx x n f x x x n n n x n x n 骣骣---鼢珑鼢--=--=?珑鼢珑鼢+++桫桫++ 故221()1n n f x x nn 骣÷ç÷?ç÷ç÷+桫. 因为0,1,2,3,,n i x i >=L ， 且121n x x x +++=L ，所以01,1,2,3,i x i <<=L n.所以221(),1,2,.1n i i n f x x i n nn 骣÷ç÷?=ç÷÷ç+桫L 所以2121(1n n f xn n 轾骣鼢?珑?犏鼢?+珑?鼢?犏珑?鼢?+桫犏臌LL即2121221()()()01n n n n n n f x f x f x x x x n n n 骣÷ç÷+++?++-?ç÷ç÷+桫L L故12()()()0n n n n f x f x f x +++?L ..…………… 14分。

7.下列有关物质的性质或应用说法正确的是 A．可以用小苏打治疗胃溃疡病人的胃酸过多症 B．金属钠具有强的还原性，可利用钠和TiCl4溶液反应制取金属Ti C．糖类、油脂、蛋白质在一定条件下均可以水解 D．在常温下，浓硫酸、浓硝酸能用铁罐储运 8．为探究NaHCO3、Na2CO3与1mol/L盐酸反应（设两反应分别是反应Ⅰ、反应Ⅱ）过程中的热效应，进行实验并测得如下数据：下列有关说法正确的是 序号液体固体混合前温度混合后最高温度①35mL水2.5g NaHCO320℃18.5℃②35mL水3.2gNa2CO320℃24.3℃③35mL盐酸2.5g NaHCO320℃16.2℃④35mL盐酸3.2g Na2CO320℃25.1℃A. 仅通过实验③即可判断反应Ⅰ是吸热反应 B. 仅通过实验④即可判断反应Ⅱ是放热反应 C. 通过实验可判断出反应Ⅰ、Ⅱ分别是吸热反应、放热反应 D. 通过实验可判断出反应Ⅰ、Ⅱ分别是放热反应、吸热反应 9.“封管实验”具有简易、方便、节约、绿色等优点，观察下面四个“封管实验”（夹持装置未画出），判断下列说法正确的是 A.加热时，①上部汇集了固体NH4Cl，说明NH4Cl的热稳定性比较好 B.加热时，②、③溶液均变红，冷却后又都变为无色 C.④中，浸泡在热水中的容器内气体颜色变深，浸泡在冰水中的容器内气体颜色变浅 D.四个“封管实验”中所发生的化学反应都是可逆反应 10. 戊醇C5H11OH与下列物质发生反应时，所得产物可能结构种数最少（不考虑立体异构）的是 A．与浓氢溴酸卤代 B．与浓硫酸共热消去 C．催化氧化 D．与戊酸催化酯化 11．根据元素周期律，由下列事实进行归纳推测，推测不合理的事实是 事实推测AAl(OH)3既能与酸反应又能与碱反应Tl（第六周期第ⅢA族）的氢氧化物Tl(OH)3也既能与酸反应又与碱反应B镁与水反应缓慢，钙与水反应较快Ba与水反应会更快C硅与 H2 在高温时反应，S与 H2 在加热能反应P与 H2 在高温时能反应DHCl在1500℃时分解，HI在230℃时分解HBr的分解温度介于二者之间12．在密闭容器中，5mol H2与2molCO2发生反应：3H2（g）十CO2（g）CH3OH（g）+H2O（g）反应达到平衡时，改变温度（T）和压强（P），反应混合物中甲醇（CH3OH）的物质的量分数变化情况如图所示。

甲 乙6 67 6 82015年普通高等学校招生全国统一考试试题（模拟）数学（文史类）本试卷共4页，共22题。

满分150分，考试用时120分钟。

★祝考试顺利★注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置，用统一提供的2B 铅笔将答题卡上试卷类型A 后的方框涂黑。

2.选择题的作答：每小题选出答案后，用统一提供的2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再填涂其它答案标号。

答在试题卷、草稿纸上无效。

3.填空题和解答题的作答：用统一提供的签字笔将答案直接答在答题卡上对应的答题区域内。

答在试题卷、草稿纸上无效。

4.考生必须保持答题卡的整洁。

考试结束后，请将本试题卷和答题卡一并上交。

第I 卷(选择题共50分)一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．在复平面内，复数21ii-对应的点的坐标是( ) (A) (1,1)--(B) (1,1)- (C)(1,1)-(D) (1,1)2.设,A B 为两个不相等的集合，条件:()p x A B ∉⋂， 条件:()q x A B ∉⋃，则p 是q 的（ ）（A ）充分不必要条件 （B ）必要不充分条件（C ）充要条件 （D ）既不充分也不必要条件3.已知32log 2a =，14log 2b =，132c -=，则,,a b c 的大小关系是( )（A ）c b a >> （B ）a b c >> （C ）b a c >> （D ）b c a >>4.阅读右边的程序框图，运行相应的程序， 则输出的K 和S 值分别为( )（A ）11，511 （B ）9，49（C ）13，613 （D ）15，7155．甲、乙两名同学在5次体能测试中的成绩的茎叶图如图所示，设1x ，2x 分别表示甲、乙两名同学测试成绩的平均数，1s ，2s 分别表示甲、乙两名同学测试成绩的标准差，则有 ( )(A) 12x x =，12s s < (B) 12x x =，12s s >开始 0S =1K =10?K >输出1(2)S S K K =++ 2K K =+结束是否(C) 12x x >，12s s > (D)12x x =，12s s =6．已知函数sin y a bx =+（0b >且1b ≠）的图象如图所示，那么函数log ()b y x a =-的图象可能是( )(A) (B)（C ） （D ）7.已知双曲线221ax by -=（0,0a b >>）的一条渐近线方程是30x y -=，它的一个焦点在抛物线24y x =-的准线上，则双曲线的方程为（ ）（A ）224121x y -= （B ）224413x y -=（C ）221241x y -= （D ）224413x y -=8.已知函数x x x f ωωcos 3sin )(-=（0ω>）的图象与x 轴的两个相邻交点的距离等于2π，若将函数()y f x =的图象向左平移6π个单位得到函数()y g x =的图象，则()y g x =是减函数的区间为（ ） （A ）(,0)3π-（B ）(,)44ππ-（C ）(0,)3π （D ）(,)43ππ9.在平面直角坐标系xoy 中，点(0,3)A ，直线:24l y x =-，设圆C 的半径为1，圆心C 在l 上．若圆C 上存在点M ，使2MA MO =，则圆心C 的横坐标a 的取值范围为（ ）（A ）]512,0[ （B ）)512,0( （C ）)3,1( （D ）]3,1[10.已知函数()1(0)f x mx x m =-->，若关于x 的不等式()0f x <的解集中的整数恰有3个，则实数m 的取值范围为（ ）（A ）01m <≤ （B ）4332m ≤< （C ）312m << （D ）322m ≤<xy O2ππ12x y4-13211O x y-1-1-2211O x y4-13211Ox y-1-1-2211O第Ⅱ卷 (非选择题共100分)二、填空题：本大题共7小题，每小题5分，共35分，请将答案填在答题卡对应题号的位置上，答错位置，书写不清，模棱两可均不得分。